非线性趋势KPSS检验、模型误设与检验流程构建

江海峰，汪忠志

(安徽工业大学 a.商学院；b.数理学院，安徽 马鞍山 243032)



江海峰a，汪忠志b

(安徽工业大学 a.商学院；b.数理学院，安徽 马鞍山 243032)

摘要：利用理论推导和蒙特卡洛模拟方法，研究非线性趋势数据生成模型中KPSS检验统计量、趋势项检验统计量分布规律，并总结出KPSS检验流程。 理论研究表明，在原假设和备择假设成立时，相关检验统计量在大样本下都收敛到维纳过程的泛函，且KPSS检验不能有效区分趋势类型，模拟研究也得出类似结论。实证研究显示，通过使用KPSS检验流程，可以精确确定数据生成过程。

关键词：KPSS检验；单位根；蒙特卡洛模拟；模型误设

一、引 言

自Phillips首次从理论上证明单位根导致伪回归以来，单位根检验日益受到重视[1]。根据假设设定形式，假设检验分为两类：以存在单位根为原假设的检验(本文称为第一类检验)，主要有ADF、PP、DF-GLS、NRS和NP检验；以序列平稳为原假设的检验，其中以Kwaitkowski等人的KPSS检验最为常用[2]。后者的检验模型如下：

yt=dt+ξt+εt

ξt=ξt-1+ut

(1)

t=1,2,…,T

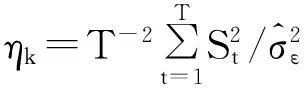
(2)

k=1,2

相对于第一类检验，KPSS检验研究相对滞后，总体来说，主要集中在以下三个方面：

一是拓展研究。例如Hobijn等人考虑d0t=0时KPSS检验统计量分布，并证实无论在哪种假设下，只要数据生成过程含d2t而估计模型含d1t，或者数据生成过程含d1t而估计模型含d0t时，检验统计量都具有一致性[3]。Hadri和Horváth等人将结构突变引入模型，并考察一个突变点时的检验统计量分布和检验效果[4-5]。Matteo等人针对d1t=c提出KPSS秩检验量，而封福育将ESTAR模型与KPSS检验相结合，考察购买力平价的非线性检验[6-7]。

三是误设研究。Carrion-i-Silvestre指出：当模型存在水平突变但突变点被误设时，KPSS检验会出现水平扭曲，扭曲程度取决于突变幅度[11]。Hadri等人则从模拟角度证实：当原假设成立时，如果数据生成d1t，而误用d2t估计，检验水平并未发生扭曲，但会过渡拒绝原假设[4]。这表明KPSS检验同时受到数据生成过程和估计模型选择的影响，一旦两者不匹配，就会得出错误结论。

显然，以上研究既丰富了KPSS检验理论，为降低水平扭曲程度和提高检验精度作出了贡献，又提示在实证分析中要正确设定KPSS检验模型。由此不难发现，上述研究视角与第一类检验完全一致，但在研究内容上，和第一类检验相比仍有几个方面值得进一步完善。

第一，Schmidt和Phillips考虑一般趋势下单位根LM检验统计量，揭示第一类单位根检验统计量分布随趋势递增的变化规律，但对含一般趋势的KPSS检验尚没有文献讨论[12]。

第二，第一类检验隐含数据生成具有二次趋势的单位根检验*对应数据生成和估计模型都含有线性趋势单位根过程，由于检验量服从正态分布，因此很少被关注。，但在KPSS检验中，已有研究最高趋势仅为线性趋势，对具有非线性二次趋势宏观经济序列而言，这显然不能满足实证分析的需要。

第三，Hobijn等人考虑数据生成为d2t(d1t)而估计模型为d1t(d0t)时检验统计量的一致性，但对反向检验模式检验统计量性质没有研究[3]；Hadri等人也仅从模拟角度考查原假设成立时，生成模型为d1t而检验模型为d2t这一特定反向KPSS检验模式[4]。显然，为全面考察KPSS检验统计量性质，理论和实证分析还要研究其它类型反向检验结论及其解释。

第四，由于单位根检验统计量分布同时受到数据生成过程与模型设置形式影响，所以单位根检验过程也是数据生成识别过程，研究表明：KPSS检验本身难以区分模型误设，故检验必须遵循一定的逻辑顺序。为此有必要为KPSS检验构建一个类似第一类检验的DJSR流程*该流程由Dolado等人提出，用于确定第一类检验中数据生成过程。，但没有文献对此进行研究[13]。

鉴于此，首先，本文研究一般趋势生成模型KPSS检验统计量分布与一致性；其次，为满足实证分析需要，给出二次趋势模型KPSS检验统计量常见临界值，在此基础上着重讨论模型误设时不同趋势项检验统计量分布与性质，导出识别趋势类型的趋势项检验统计量分布与常见临界值；再根据模型误设检验结论构建KPSS检验流程；最后，使用该流程进行实证分析。本文揭示了KPSS检验统计量分布随趋势递增而变化的规律，完整地导出模型误设理论，并系统地提出KPSS检验流程，实证研究介绍了如何使用该检验流程完成检验，因而本文具有较强的理论价值和实践指导意义。

二、非线性趋势模型KPSS检验

(一)检验统计量的渐进分布

设数据生成过程为：

yt=β0+β1t+β2t2+…+βm-1tm-1+ξt+εt

ξt=ξt-1+ut

t=1,2,…,T

(3)

yt=β0+β1t+β2t2+…+βm-1tm-1+εt

(4)

构造如下检验统计量：

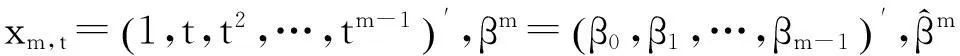
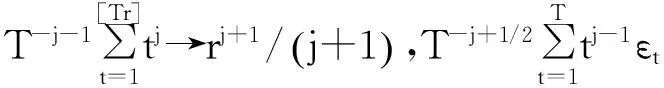
dW(r)

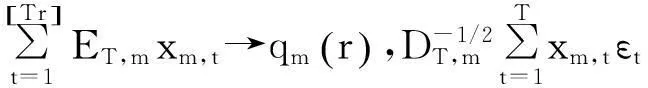
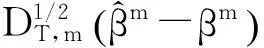
(5)

另一方面有：

(6)

据此得到：

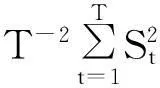
(二)检验统计量的一致性

接下来讨论该检验统计量在备择假设成立时的性质，定理2给出了结论。

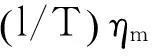
(7)

所以有：

利用此结论得到：

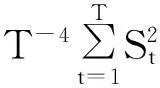
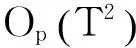
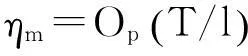
三、二次趋势KPSS检验统计量

宏观经济序列往往会呈现出非线性趋势，但很少超过二次趋势，因此需要单独考察m=3时检验统计量临界值与模型误设时检验统计量的性质。

(一)检验统计量分布与临界值

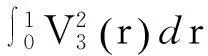
表1　部分样本下η3常见临界值模拟结果

(二)模型误设检验统计量性质

定理2表明η3具有一致性，从而具有较高的检验功效，但这仅当m都为3且模型正确设定时的结论。如果真实模型中m分别为1、2、4以及零均值平稳模型和单位根过程，而估计模型都为二次趋势平稳过程，则检验结论如何呢？为便于说明和不失一般性，假设εt和ut均为无关独立同分布过程。

考察m为1、2和零均值的检验结论，即假设数据生成过程分别为：

yt=β0+β1t+β2t2+εt

(8)

t=1,2,…,T

yt=β0+β1t+β2t2+ξt+εt

(9)

ξt=ξt-1+ut

t=1,2,…,T

其中式(8)对应趋势平稳过程，式(9)对应单位根过程。当考察零均值模型时有β0=β1=β2=0，当m为1时有β0≠0,β1=β2=0，当m为2时有β1≠0,β2=0。估计模型为：

yt=b0+b1t+b2t2+vt

(10)

则有定理3成立。

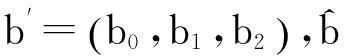
(11)

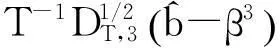
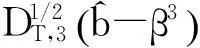
故

(12)

从而有：

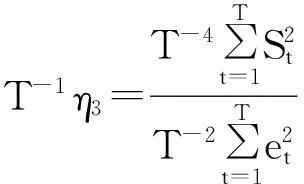
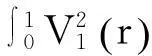
推论1表明：如果数据生成是非零均值平稳过程，而误用线性趋势模型进行KPSS检验，检验统计量η2分布与数据生成和估计都与线性趋势模型结果完全相同，这从理论上解释了Hadri等人的模拟实验结果。显然，定理3及其推论拓展了Hobijn等人的反向检验结论。

再考察m为4时的结果，即假设数据生成过程分别为：

yt=c0+c1t+c2t2+c3t3+εt

(13)

yt=c0+c1t+c2t2+c3t3+ξt+εt

(14)

ξt=ξt-1+ut

其中c3≠0，式(13)对应趋势平稳过程，式(14)对应单位根过程，而估计模型仍为式(10)，则有如下定理4成立。

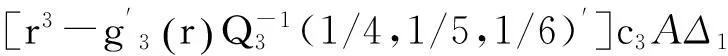
因此有：

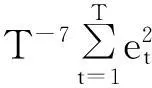
从而得到：

若数据生成为式(14)，由于t3在数据生成过程中起支配作用，单位根成分ξt作用被湮没，相关结论与式(13)相同，故定理4成立。定理4拓展了Hobijn等人的结论。

(三)蒙特卡罗模拟分析

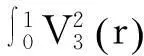
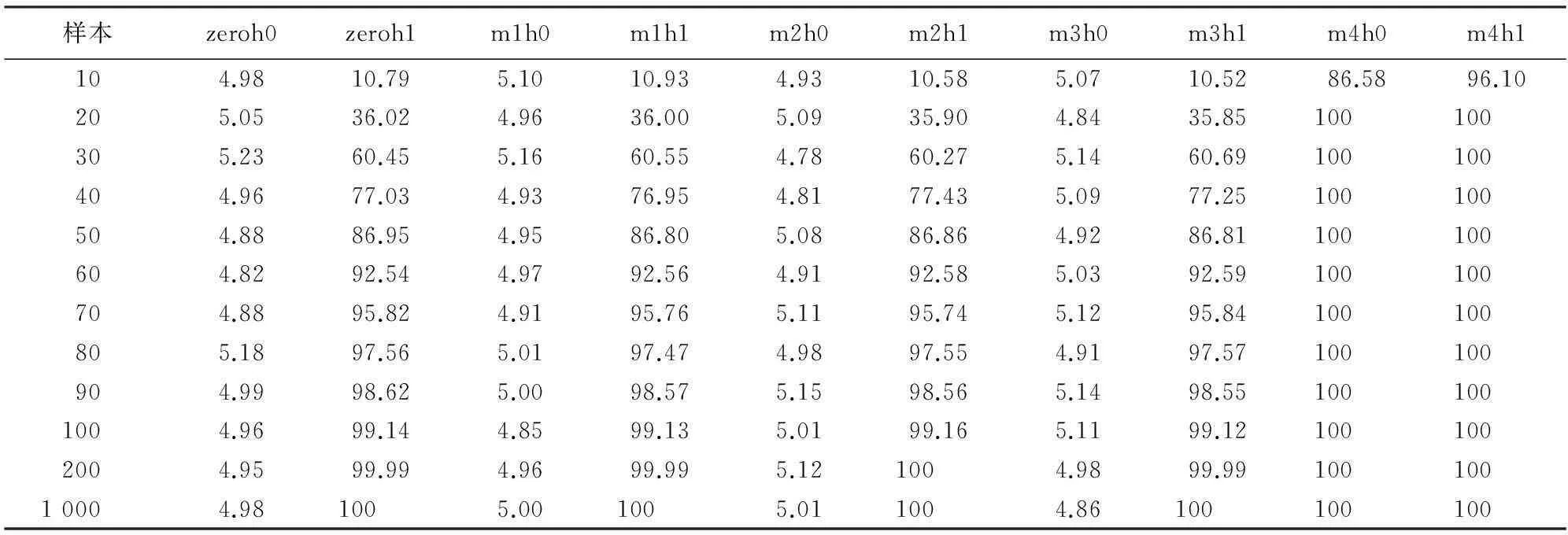
表2　不同数据生成模型下的模拟结果　(单位：%)

四、趋势项检验统计量分布与KPSS检验流程

(一)趋势项检验统计量分布

定理3表明，即使数据生成中m为1、2或者均值为零，当原假设和备择假设分别成立时，检验统计量η3的性质与m为3时完全相同。因此，当以式(10)估计并执行假设检验时，如果接受原假设，此时还需进一步判断m值，当备择假设成立时亦是如此，这实际上就是检验式(8)、(9)中趋势项参数βi=0,i=0,1,2是否成立，推论1和推论2也类似表明需要对模型中趋势类型进行识别。鉴于实际经济序列趋势很少超过二次，本文不讨论m为4时的参数检验。当原假设成立时，式(8)中βi=0检验可以使用普通t检验，本文不作介绍，但对备择假设成立的式(9)而言，相关检验统计量分布收敛到维纳过程的泛函，需要使用模拟方法得到临界值。下面分析备择假设成立时趋势项检验统计量的分布。

先建立假设H0:β2=0，此时数据为一次趋势附带单位根过程，根据式(11)有：

此分布中含未知量σu，不能直接用于检验。根据式(12)并结合原假设H0:β2=0成立有：

检验统计量t2不含未知成分，可以检验假设H0:β2=0。对于检验H0:β1=0和H0:β0=0，对应数据分别为非零均值和零均值并附带单位根过程，相应估计模型为式(10)中分别剔除b2和b1的结果。根据以上推导过程类似得到：

为在实证分析中应用上述检验统计量，需要给出相应的临界值，限于篇幅，表3仅给出检验统计量t2常见临界值的模拟结果。

表3　检验统计量t2不同样本下的临界值模拟结果

(二)KPSS检验流程

为得到正确的检验结论，防止模型误设，根据模型误设检验结论和趋势项检验统计量分布结果，总结KPSS检验流程如下：

步骤一：以式(10)为基础进行KPSS检验，如果接受原假设，进入步骤二，否则进入步骤三；

步骤二：分别估计二次趋势、一次趋势和非零均值的模型，并分别对模型中的二次趋势项、一次趋势项和非零均值项使用普通t检验统计量进行显著性检验，确定模型最终趋势类型；

步骤三：在式(9)中利用检验统计量t2检验假设H0:β2=0，如果拒绝原假设，表明模型为二次趋势并附带单位根过程，否则进入步骤四；

步骤四：在式(9)中令β2=0，重新估计一次趋势模型，利用检验统计量t1检验假设H0:β1=0，如果拒绝原假设，表明模型为一次趋势并附带单位根过程，否则进入步骤五；

步骤五：在式(9)中令β1=β2=0，再次估计非零均值模型，利用检验统计量t0检验假设H0:β0=0，如果拒绝原假设，表明模型为非零均值并附带单位根过程，否则为零均值附带单位根过程。

五、实证研究

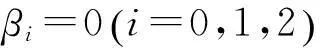
表4　6个序列平稳性检验结果

显然，使用本文KPSS检验流程也得到了与第一类检验相同的结论，与第一类检验DJSR流程相比，不需要计算联合检验统计量，因而更为简便。

六、结 论

通过以上研究，本文得到以下结论。

一般趋势KPSS检验理论研究表明：若数据生成为m阶趋势平稳过程时，KPSS检验统计量收敛到m阶布朗桥过程的泛函。当数据生成是m阶趋势单位根过程时，KPSS检验统计量具有一致性，该研究推广了已有结论。

二次趋势模型KPSS检验统计量临界值模拟表明：该临界值对样本变化呈现出稳定态势，因此可用于呈现二次趋势变量的平稳性检验，该结果拓宽了实证分析范围。

模型误设理论研究表明：使用KPSS检验必须同时确定模型中趋势类型，该分析解释了Hadri等人的模拟实验结果，进一步完善了KPSS检验模型误设检验理论。

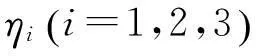
参考文献：

[1]Phillips P C B. Understanding Spurious Regressions in Econometrics[J]. Journal of Econometrics, 1986(3).

[2]Kwiatkowski D, Phillips P C B, Schmidt P, Shin Y. Testing the Null Hypothesis of Stationarity Against the Alternative of a Unit Root: How Sure are We that Economic Time Series Have a Unit Root? [J].Journal of Econometrics, 1992(1).

[3]Hobijn B, Franses P H, Ooms M.Generalizations of the KPSS Test for Stationarity[J]. Statistica Neerlandica, 1998(4).

[4]Hadri K, Rao Y. KPSS Test and Model Misspecifications[J].Applied Economics Letters,2009(12).

[5]Horváth L, Kokoszka P, Rice G.Testing Stationarity of Functional Time Series[J].Journal of Econometrics,2014(1).

[6]Matteo M Pelagatti， Pranab K Sen.Rank Tests for Short Memory Stationarity[J]. Journal of Econometrics,2013(1).

[7]封福育.中、日、韩长期购买力平价的非线性检验——基于1994—2009年的经验分析[J]. 统计与信息论坛,2011(1).

[8]Kurozumi E,Tanaka S. Reducing the Size Distortion of the KPSS Test[J]. Journal of Time Series Analysis, 2010(6).

[9]Sul D, Phillips P C B, Choi C Y. Prewhitening Bias in HAC Estimation[J]. Oxford Bulletin of Economics and Statistics, 2005(4).

[10]Amsler C, Schmidt P,Vogelsang T J. The KPSS Test Using Fixed-b Critical Values: Size and Power in Highly Autocorrelated Time Series[J].Journal of Time Series Econometrics,2009(1).

[11]Carrion-i-Silvestre J L. Breaking Date Misspecification Error for the Level Shift KPSS Test[J]. Economics Letters, 2003(3).

[12]Schmidt P, Phillips P C B. LM Tests for a Unit Root in the Presence of Deterministic Trends[J]. Oxford Bulletin of Economics and Statistics, 1992(3).

[13]Dolado J,Jenkinson T, Sosvilla-Rivero S. Cointegration and Unit Roots[J]. Journal of Economic Surveys, 1990(3).

[14]Phillips P C B，Perron P. Testing for a Unit Root in Time Series Regression[J]. Biometrika, 1988(75).

[15]Nelson C R, Plosser C. Trends and Random Walks in Macroeconomic Time Series: Some Evidence and Implications[J]. Journal of Monetary Economics,1982(10).

(责任编辑：李勤)

汪忠志，男，安徽安庆人，教授，硕士生导师，研究方向：金融数学，信息论。

【统计理论与方法】

KPSS Test for Nonlinear Trend, Model Misspecification and Construction of Test Process

JIANG Hai-fenga， WANG Zhong-zhib

(a. School of Business; b. School of Mathematics and Physics, Anhui University of Technology, Ma'anshan 243032, China)

Abstract:Based on the theoretical deduction and Monte Carlo simulation, this paper studies the distribution of KPSS and trend test statistics for data generation process with nonlinear trend, and the KPSS test process is also summarized. The theoretical research shows that these test statistics converge in large samples to the function of Wiener process under the null hypothesis and alternative hypothesis, and that the KPSS test can not effectively distinguish the trend type. Similar conclusions are drawn from simulation results . Empirical research indicates that the data generation process can be accurately determined through the use of the KPSS test procedure.

Key words:KPSS test; unit root; Monte Carlo simulation; model misspecification

中图分类号：O211.6∶F224.0

文献标志码：A

文章编号：1007-3116(2015)12-0009-08

作者简介：江海峰，男，安徽巢湖人，管理学博士，副教授，硕士生导师，研究方向：数量经济理论及应用；

基金项目：国家社会科学 《基于Bootstrap方法下单位根检验研究》(13BJY011)；安徽省高校优秀青年人才计划重点项目

收稿日期：2015-04-30