美国进出口贸易总额预测方法简化研究——基于包含突变点的单位根检验及ARIMA模型

牛睿　中国人民大学经济学院



美国进出口贸易总额预测方法简化研究
——基于包含突变点的单位根检验及ARIMA模型

牛睿中国人民大学经济学院

摘要：ARIMA模型是经济学研究中一个重要的预测模型，并有多年的使用历史。而单位根是否存在是该模型一个重要前提基础。同时多数经济数据由于结构性的原因，无法通过单位根检验，常常需要差分处理，这无疑增加了ARIMA模型的复杂程度。基于近年来的统计分析理论，特别是包含突变点的单位根检验理论，简化ARIMA模型复杂度。最后以美国1992年-2015年进出口贸易总额数据做了实证分析，结果比较满意。

关键词：ARIMA 突变点 单位根 进出口总额 预测

一、引言

ARIMA模型是经济学研究中一个重要的预测模型，并有多年的使用历史。而单位根是否存在是该模型一个重要前提基础。同时多数经济数据由于结构性的原因，无法通过单位根检验，常常需要差分处理，这无疑增加了ARIMA模型的复杂程度。然而是否能通过一定的统计原理降低ARIMA模型复杂程度，进而进一步推广ARIMA模型的使用范围，有着一定的研究意义。

二、相关理论

（一）ARIMA模型

ARIMA(Autoregressive Integrated Moving Average Model)，由Box和Jenkins（1970）提出，用于时间序列的分析及预测。ARIMA模型通常表示为ARIMA（P，D，Q），其中参数P，D及q要求为非负整数，p为自回归模型阶数，d为差分阶数，q为模型移动项数。ARIMA模型是Box-Jenkins方法中时间序列模型的重要组成部分。三个参数中两个参数为零时该模型可缩写为“AR”，“I”或“MA”。例如：ARIMA （1,0,0）是AR（1），ARIMA（0,1,0）是I（1），ARIMA（0,0,1）是MA（1）。ARIMA模型的基本思想是：将预测对象随时间推移而形成的数据序列视为一个随机序列，用一定的数学模型来近似描述这个序列。这个模型一旦被识别后就可以从时间序列的过去值及现在值来预测未来值。ARIMA模型在经济预测过程中既考虑了经济现象在时间序列上的依存性，又考虑了随机波动的干扰性，对于经济运行短期趋势的预测准确率较高，是近年应用比较广泛的方法之一。

（二）BP检验

突变点（Outlier 或 Breakpoint ），其检验早期研究见于Chow（1960）基于F-statistic检验已知突变点及Andrews（1993）和Andrews and Ploberger（1994）推导出的Quandt极限分布及相关统计量检验。BP检验是近年来发展起来的用于检验多结构突变点的完备估计方法,包括突变点估计值的连续性、突变点次数检验以及对突变点置信区间的估计。Bai 和 Perron （1998）研究了在最小二乘数回归模型中突变点的估算模型，其模型很好的估计了未知突变点及突变点数量。随后Bai 和 Perron（2003）进一步讨论了突变估算模型的实际应用，并完善了模型，模型在全局及局部突变显示了着良好的估算能力。并且根据多种理论研究了置信区间断裂日期问题以及整体数据中误差估算问题。

（三）包含突变点的单位根检验(Unit root test with breakpoint)

ARIMA模型所依赖的的一个重要的前提就是数据能通过单位根检验，即是平稳的（stationary）。如果存在单位根，则需要考虑差分稳定（difference stationary）。单位根的存在表明经济环境中的冲击将带来永久性影响，如果这样在引入模型后其解释能力会变得不理想。同时以往学者研究中发现多数宏观数据是无法通过单位根检验。

最早有学者Nelson 和 Plosser (1982)对美国 14 个主要经济数据做了单位根检验，其中13个数据都是非平稳的。而后Perron 首先对这一结论提出质疑：由于单一时间序列单位根检验的检验势（power）较低，若时间序列数据是由一次结构变动的趋势平稳过程产生的，则单位根检验可能会错误地接受存在单位根的原假设。Perron (1989)提出未考虑结构变化的单位根检验功效较低, 通过先验信息选择外生结构变化的单位根检验给出了完全不同的结论:绝大多数 (11/14)总量是分段趋势平稳 (segmented -trend-stationary) 的 。但 Perron 的检验的一个缺陷是假定发生结构突变的时间已知，即将结构突变的估计外生化，Christiano 指出这很可能会导致单位根检验对原假设的过度拒绝。Zivot 和 Andrew (1992) 将结构断点选择过程内生化, 对Nelson 和 Plosser (1982)所选取的样本重新进行了无条件单位根检验, 在渐近分布和有限样本情况下, 近半数总量无法拒绝非平稳原假设。鉴于我们无法确定所考虑的区间只有一个结构变化 , Lumsdaine 和 Papell (1997) 将Zivot 和Andrew (1992)的方法扩展到两个结构断点的情形, 结果得出更多的总量是分段趋势平稳的结论。

三、其他学者研究

王琨等（2007）对中国9项宏观数据进行了分析，其中7项（含中国进出口总额）在数据考虑突变点结构后显示了非线性平稳性。

四、美国进出口贸易数据实证

这里选取了美国商务部经济分析局1992年-2014年进出口贸易总额数据（IDS0182 Census-based NSA）。美国进出口贸易数据来源有很多，选取BEA数据来源主要原因有二：一是该数据是目前知道少有以月为单位的，这样能增加样本总量，提高ARIMA模型预测准确度；二是该数据直接从商务部的普查数据汇总而成，没有多余的二次调整，降低不可知数据调整对模型分析带来的影响。数据汇总见图（1）：

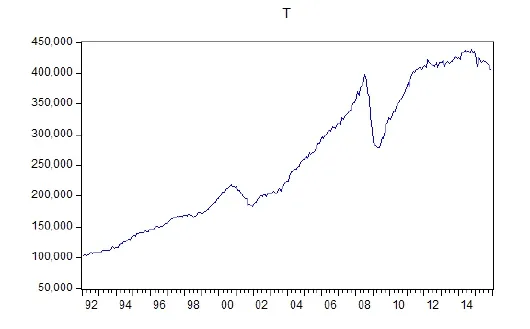
图（1）美国进出口总额1992年-2014年数据

数据取对数，然后引入单位根检验。在这里选择使用ADF和KPSS检验。检验结果见表（2）：

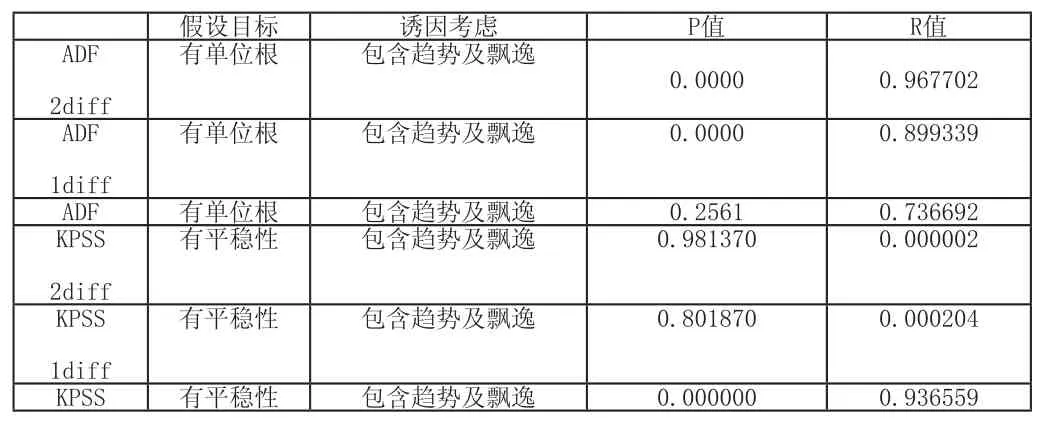
表（1）ADF及KPSS检验结果

根据上表所示，原始数据明显具有单位根，无法通过平稳性检验，而数据一阶差分结果通过平稳性检验。按照原有理论需对数据进行一阶差分处理，然后再引入ARIMA模型。这里我们采用与以往不同的数据处理方法。基于图（1），发现数据具有明显的上升趋势，以及多处剧烈波动（例如2001年2月、2009年3月附近。）于是假设数据含有突变点，使用BP breakpoint model进行检验。通过BP breakpoint model对数据进行突变点检验，表明存在突变。有学者基于Perron （1989），总结出断点数据四种基本模型:

1 无趋势的偏移的突变结构：

2 有趋势的偏移突变结构：

3 有趋势的偏移及趋势突变结构：

4 有趋势的趋势突变结构：

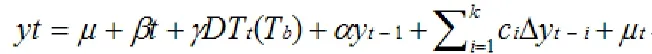
借用Eviews9，基于以上四个基本模型对数据进行包含突变的单位根检验，其结果如图（2）。检验假设为数据存在单位根，而P值表明数据拒绝原假设，R表明解释程度较好。

图（2）

将数据导入ARIMA模型，由于数据通过单位根检验，可以将ARIMA模型退化成ARMA模型考虑。进行自相关检验（ACF）及偏自相关检验（PACF）。图（3）为检验结果。

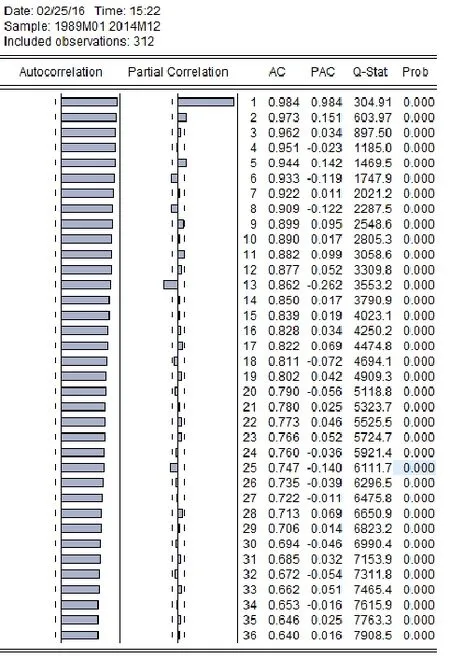
图（3）

根据图形所示，结合一般性经验，估计ARMA模型的（p，q）值为（1，0），从而ARMA模型退化为AR（1）模型。将数据引入并计算。

最后进行传统ARIMA模型预测，由于数据无法通过ADF检验，ARIMA最后取值为（3，1，3）。图（4）为两次检验结果。从结果可以看出整体预测差异不大。

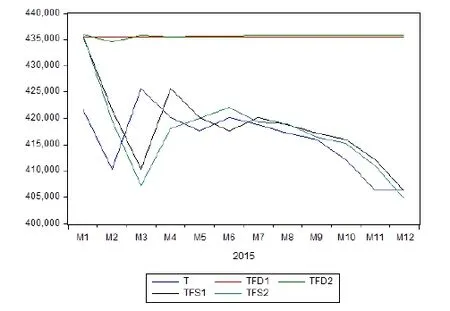
图（4）

五、总结

在美国进出口总额实例分析中，由于考虑包含突变的单位根检验，简化了原有ARIMA模型，将原有ARIMA（3，1，3）模型退化为AR（1）。同时将结果对比也较满意。在此方法推广时也应该注意到，目前研究对同时处理多个突变点结果不是非常理想，可以考虑分段式处理方法。但是分段式本身也加大了模型的处理复杂程度与本文初衷相反。所以本文涉及的处理方法尚有不足之处，有一定的局限性。

参考文献：

[1 ]Box, George; Jenkins, Gwilym (1970). Time Series Analysis: Forecasting and Control.

[2] Pierre Perron(2006).Dealing with Structural Breaks.

[3] Jushan Bai and Pierre Perron(1998).Estimating and Testing Linear Models with Multiple Structural Changes.

[4] Jushan Bai and Pierre Perron（2003）.COMPUTATION AND ANALYSIS OF MULTIPLE STRUCTURAL-CHANGE MODELS

[5] 王琨，滕建州，石凯，(2012) 中国宏观经济和金融总量的非线性研究

[6] 李子奈，周建，(2005) 宏观经济统计数据结构变化分析及其对中国的实证

作者简介：牛睿，中国人大学经济学院实验室，实验室（中级）。