数学直观的深度发展之路

杨建

摘 要：学生教学直观能力的发展不是简单易成的，它是呈螺旋式的上升发展，教师可以借助图形特象、迁移知识及有序推理等方式来推动学生直观能力的形成。

关键词：数学直观;发展

中图分类号：G623.5          文献标识码：A     文章编号：1992-7711（2015）24-093-1

2011年版的《数学课程标准》再次提出“直观”概念，并强调：“要借助‘直观把复杂的数学问题变得简单化，把繁琐的推理变得直观化，帮助学生直观地理解数学，进而有助于他们快速地寻找到解决问题的思路。”这一概念的提出，给数学的教学与学习提供了新的思路与契机。然而尽管新的《数学课程标准》推行了三年有余，“直观”却没走进学生的世界，究其原因，是我们对“数学直观”的理解出现偏差;要知道，学生的思维发展是呈螺旋式的发展，即学生思维的发展是经历从“直观形象思维→抽象逻辑思维→新的直观形象思维→新的抽象逻辑思维”螺旋上升的发展过程。所以，我们教师在教学中，既要关注学生的“直观形象思维”形成，又要帮助他们从“初始直观形象思维”向“初步抽象逻辑思维”转换，更要帮助学生将“初步抽象逻辑思维”转化成“新的直观形象思维”，只有这样，才能帮助学生形成数学直观。

一、数学直观根植于图形物象

“数学直观是人脑对客观事物及其关系的一种直接的识别或猜想的心理状态。”然而我们也知道“数学直观”是建立于学生对数学直观理解的基础上，我们只有根植于图象，即用图象的直观性帮助学生产生“直观理解与判断”，才能帮助学生提升他们的直观思维，进而形成数学直观的能力。

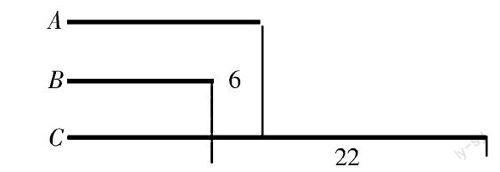
例如“数量关系”的教学。“数量关系”对于小学生来说，既是“抽象的”，又是“直观的”。说其“抽象”是缘由小学生需要经历“抽象”后才能理解“数量关系”;说其“直观”是缘由这些数量关系可以借助图形等直观的手段显示，并可以被“直观”的理解。如：有三个商人，他们都赚了若干钱，A商人比B商人多赚6万元，C商人是A商人的两倍，比B商人多22万元，请问他们一共赚了多少钱？这是一个典型的数量关系应用题，从题目上看，A、B、C三者间的关系错众复杂，学生很难对这些数量关系产生直观的理解，更为重要的是，A、B、C三者中，没有一个是具体值，此时就可以借助图形来产生直观的理解。如

从这个线段图中，我们就可以直观地把握ABC三者的关系，也可以直观计算三者之和。第一种方法先计算各人所赚：A商人所赚的钱数——“22-6=16”，当A商人的钱数算出后，B和C商人的钱数也就随之而解——16-6=10;16*2=32。三者相加16+10+32=58（万元），这样，在图形的帮助下，学生就可直观理解这组繁杂的数量关系。第二种方法从整体出发，将“A”看作一个单位，三者和就是（22-6）*4-6=58。这样有了图象的帮助，数学的理解与判断也就直观了。

二、数学直观累积于不断迁移

俗话说：“厚积而薄发。”数学直观作为一种思维活动，也自然离不开积累与迁移，学生在数学学习过程中，由于经验的不断积累，知识的不断丰富，就自然会将一些知识、方法、思考步骤进行迁移，在教学时，如果我们教师在教学新知时，利用迁移的策略，帮助学生梳理出新旧知识的迁移点，并依此进行教学，就可帮助学生产生对新知的直观理解与把握。

例如分数的数量关系教学。自分数与百分数出现以后，与它们相关的数量关系的运用也随之出现，为了让学生直观地把握分数的数量关系，我在教学时，就采用了“迁移”的策略：首先呈现整数的数量关系，“（1）甲数是20，乙数是甲数的4倍，乙数是多少？（2）甲数是20，是乙数的4倍，乙数是多少？”面对这两种数学关系，我先是用线段图的策略帮助学生巩固、加深对这种数学关系的理解;接着我将这个题目中的整数变成分数，“（1）甲数是20，乙数是甲数的1/4，乙数是多少？（2）甲数是20，是乙数的1/4，乙数是多少？”由于有了整数数量关系的铺垫，再加上“线段图”的暗示，学生自然而然地“直观地”把握这两个题目的解决策略。

三、数学直观通达于有序推理

数学直观的形成不仅依赖于“有形”的物象、“长期”的经验，更依赖于有序的推理。小学生的推理能力还处于雏型期，他们的大脑还没有形成有序的认知结构，也没形成有序的分析能力，这种现状就决定我们在教学时，要遵循“有序”的原则，从“图形”到“文字”，从“文字”到“关系”，从“关系”到“思维”……一步步形成思维过程，一步步地建立起“图式”认知系统，从而形成“从一般现实世界里总结出数学策略、思想”的直观能力。

例如《正比例的意义》的教学。“比例”是一种数量之间的对比关系，因为它暗含“渐变”的元素，故而“比例”常常成为学生难以理解与把握的领域。然而一旦学生掌握或认同“比例”及其“渐变”的法则，则将帮助学生更加直观地理解数学深层奥妙。为此我在教学时，采用“有序推理”的原则，一步步将学生带到“渐变”的世界中：首先我采用“以图促解”的策略，即让学生用“描点法”画出表格中的数据所对应的点数图形，接着领导学生对照“所描出的点”与“表中的数据”的关系，让学生初步感受“点与数”以“某种规律”呈现，以初步建立“渐变”的物象图形;接着再引导学生总结感受数的变化与点的变化之间的关系，从而在脑海里初步形成“一一对应”的感知;最后，进一步拓展，使学生在图形的参照下，感受两种量同时扩大或缩小的变化规律。这样从“图形”到“数据”，从“数据”到“规律”一一呈现，学生就自然而然地领会“比例”的真谛。

总之，学生数学直观能力的形成不是一蹴而就的，它不仅需要经历一系列的感悟、迁移、推理，更需要我们教师不断地探究、引领、笃行。