多频率衰减振动系统阻尼参数识别

第一作者霍兵勇男，博士，讲师，1979年生

多频率衰减振动系统阻尼参数识别

霍兵勇，易伟建

(湖南大学土木工程学院，长沙410082)

摘要：自由衰减信号在工程应用中十分常见，从冲击响应信号中识别真实准确的谐波参数就成为实验研究的关键，相关的参数识别研究不断深入，介绍一种识别阻尼的方法，包括3方面内容：①考虑自由衰减信号的谐噪比和阻尼因素，讨论了两个因素对参数识别的影响。②针对不同频率谐波的参数识别，先进行必要的信号前处理：截取有效信号长度后再截取周期整数倍部分，对称增加一倍信号。③用细化频谱识别谐波频率和初相位，反卷积方法识别谐波振幅的真实衰减过程。仿真模拟和实验信号分析证明理论方法的可行性和优越性，即无需假设阻尼模型，识别得到的谐波振幅随时间变化的时域序列。为实验揭示系统阻尼特性提供一种实用有效的技术方法。

关键词：冲击响应；细化频谱；谐噪比； 阻尼比； 反卷积

收稿日期：2013-10-21修改稿收到日期：2014-07-30

中图分类号:TN911.72文献标志码：A

Damping parameter identification by using free-decay response with the help of discrete deconvolution technique

HUOBing-yong,YIWei-jian(College of Civil Engineering, Hunan University, Changsha 410082, China)

Abstract:The free-decay response (FDR) of dynamical system has been widely used for the identification of structural parameters in many fields of engineerings, and comprehensive studies results have been available in related literatures. A new approach was proposed for identifying the damping ratio by using FDR. The approach includes three main contents: ①analyzing the accuracy of the identified parameters in consideration of the influences of damping ratio and harmonic-to-noise ratio (HNR); ②for different frequency harmonics, performing the necessary preprocessing of the digital signal, i.e. intercepting a whole number of multiples of harmonic period from an effective signal, and symmetrically doubling the signal; ③using discrete deconvolution technique in the identification of damping ratio. The results show that the proposed approach is capable of identifying the structural parameters with acceptable accuracy, and provides an efficient way for revealing the structural damping characteristics and estimating the structural parameters. The approach does not need to depend on a prior knowledge of damping model, and the time sequence reflecting the change of harmonic amplitude can be achieved.

Key words:free-decay response; zoom spectrum; harmonic to noise ratio; damping ratio; discrete deconvolution

冲击响应信号在工程应用中非常普遍[1-4]，其参数识别方法也有广泛讨论[5-7]，冲击响应信号中往往含有多个频率谐波，各频率谐波信号不断衰减最终都淹没在噪声中，实践中采集信号的长度一般依照信噪比(SNR)；多数研究中识别方法的数值模拟采用高斯白噪声(Gaussian noise)[8]，有的还进一步讨论了瞬时SNR，但自由响应信号中高频谐波信号衰减的时间往往较短，信号中各频率谐波的参数识别，都用同样的信号长度，而没有对具体频率谐波的衰减情况选择合适的信号长度，谐噪比(Harmonic to Noise Ratio,HNR)是某个频率谐波信号对噪声的比率，是关系到具体频率谐波参数识别的直接因素，谐噪比在过去研究中已有关注[9-10]，但在冲击响应信号的参数识别研究中较少注意这一因素。

现有识别方法和设计中一般对阻尼采用非比例[11-13]或者比例假设[14]，依赖这些假设模型，在应用中常常带来不确定因素，实际结构冲击响应中谐波振幅的真实变化仍然未知；工程应用中不同方法识别得到的频率一般都比较吻合，但阻尼比的值却有差异。

本研究采用细化频谱方法识别谐波频率和初相位，讨论了HNR和阻尼比对冲击响应信号频率和初相位识别的影响，进而应用离散傅里叶变换(DFT)卷积和反卷积性质，实现了对冲击响应信号的参数识别；识别过程中对信号采取了一系列的必要前处理措施，这些措施与参数识别的原理紧密结合，并有一定通用性；对阻尼的识别得到谐波振幅的真实变化过程，为实际工程中动力实验方法探索结构阻尼特性提供一种实用的数字信号参数识别方法。

1HNR和阻尼比对频率和初相位识别的影响

自由衰减信号中一般包含多个频率谐波，表达式可以写成：

(1)

式中：f为谐波频率，A为振幅，θ为初相位，ζ为阻尼比；

由于噪声的存在，实际工程中采集的自由响应信号最终会消失在噪声中，其中高频谐波信号衰减的时间往往较短，低频谐波未完全衰减的时候，高频谐波早已被噪声淹没，若把自由衰减信号依次分段，对每段信号分别进行DFT，不妨把频谱峰值明显的时域信号区段称作对该谱峰对应的频率谐波的有效信号。这样在识别自由衰减信号的各个谐波参数时，可以先确定各频率谐波信号的有效信号长度，以减少无效信号带来的误差。

经典DFT分析是信号频谱分析的一种基本方法，DFT的表达式[15]：

(2)

(3)

式中：ω=2π/T，T为信号时长，t为采样间隔，ω为频域间隔

但是DFT分析中由于基函数在分析信号长度上都是整周期，因此频率的取值受到限制。而细化频谱打破这种限制，其计算表达式如下：

(4)

细化频谱表达式中的基函数在信号长度T上不一定是整数倍周期，这样就能使数字信号的谐波发生共振而使幅值频谱达到最大限度的峰值，更精确定位谐波的频率和初相位。

采用细化频谱方法分析HNR和阻尼对频率和初相位识别的影响，为了应用上的方便，这里对有阻尼频率和无阻尼频率不加区分，这样表达响应结果对参数值的影响很小[16]。单频率情况下，SNR和HNR意义完全相同，因此用HNR表示信号和噪声的对比关系，HNR是关系谐波参数识辨精度的真实因素，在谐波频率和初相位识别时，舍去所分析信号中HNR较低的区段，可以提高谐波参数识别的精度。无噪声时，认为HNR=∞；单频率谐波情况下假设参数取值：A=4/3，f=100+1/3 Hz，θ=0，阻尼比采用相应曲线中横坐标对应值，代入式(1)中，采样长度T=1 s，采样点数N=1 024，生成数字信号。图1是不同HNR(加入高斯白噪声，单位dB)情况下细化频谱识别频率误差f*(识别值-理论值)和初相位误差θ*(识别值-理论值)随阻尼比的变化；HNR越大，则越接近无噪声时的误差，反之则识别误差变化越大；无噪声时，阻尼越高识别值误差越大。

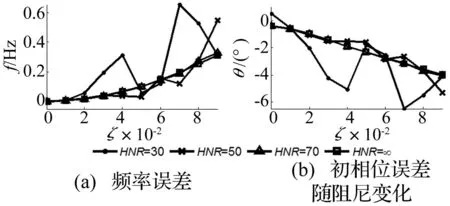
图1　不同HNR情况下细化频谱识别 Fig.1 Frequency error f * and initial phase error θ * (identified by zoom spectrum) against damping ratio with different HNR

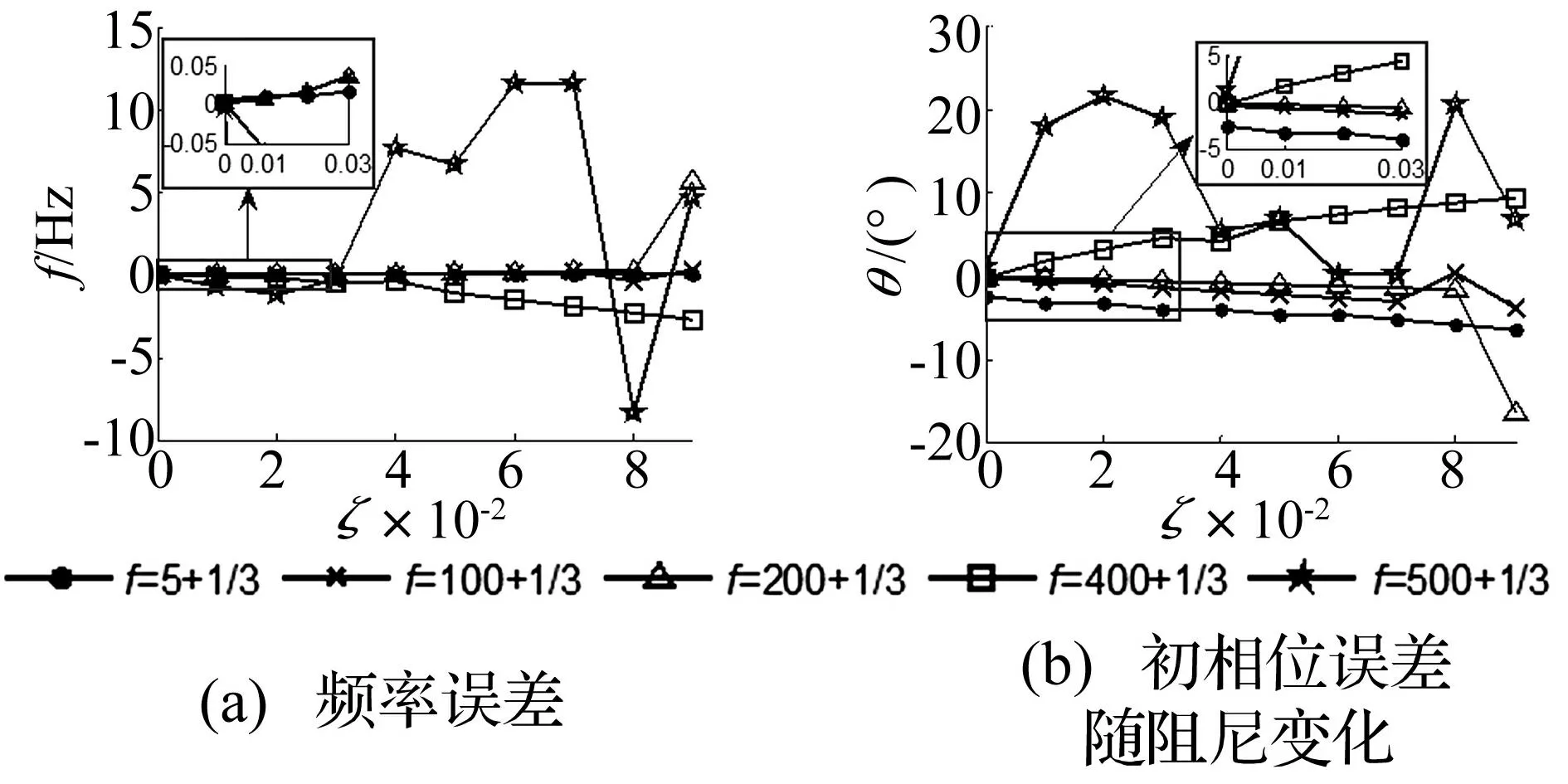
图 2　不同频率谐波细化频谱识别的频率误差和 初相位误差随阻尼比的变化情况 Fig.2 frequency error f * and initial phase error θ * against damping ratio with different frequency harmonic without noise

图2是对不同频率谐波无噪声数字信号进行参数识别得到的频率误差和初相位误差随阻尼比的变化情况，很明显高频谐波识别误差均明显增大。Shannon采样定理描述了在有效分析频域区间内出现某一频率频谱的最小采样间隔，对有阻尼信号最高频率成分每周期内的至少采样4点，阻尼比高于0.02建议采样10点以上，以避免因采样频率低给参数识别带来的较大误差。在采用某频率谐波有效长度和保证一定采样频率的情况下，总体来说阻尼越高频率和初相位的识别误差略微增大，初相位和采样频率等参数不同，识别误差的差异较小；图2的分析结果表明：阻尼比在0.03以内，频率误差一般不超过0.05倍DFT的频率间隔，初相位误差一般不超过5°。在以上分析中，横纵坐标都已有归一化意义，分析结果具有普遍性。

2识别阻尼的反卷积方法

卷积性质是DFT的重要性质之一，一般来说识别系统的冲击响应时可以利用反卷积性质[17]，为说明本文利用离散反卷积性质识别阻尼的原理，把式(1)中按单频率谐波的自由衰减信号采样得到的数字信号序列写成：

x3(kt)=x1(kt)x2(kt)

(5)

其中：

x1(kt)=cos(2πfkt-θ)，x2(kt)=Ae-ζ2πfkt

(6)

相应的DFT：

X1(nω)=DFT[x1(kt)]

X2(nω)=DFT[x2(kt)]

X3(nω)=DFT[x3(kt)]

(7)

依据离散信号的卷积性质[18]有如下关系成立：

x3(kt)=x1(kt)x2(kt)⟺X3(nω)=

(8)

实验中记录冲击响应序列x3，频谱分析可以得到x1的频率和相位，DFT得到频域序列X3和X1，通过反卷积求解X2，对X2进行IDFT便可得到x2；由于单边指数衰减信号周期延拓时，信号连接处存在较大跳跃，频谱分析会出现边界效应，此种情况一般是把识别信号两端受影响的数据舍去，再进行参数识别[19]，给参数识别带来一定不利影响；将x2通过对称增加一倍信号变成双边指数衰减来避免跳跃，同时还要信号长度是x1的周期整数倍，依据x1的相位确定是轴对称还是点对称，保证不因对称增加信号长度而使x1产生跳跃而发生频率泄露(为充分保证初相位识别值的精度，一般在相位对称处截取时，谐波一个周期内采样点数>100)；这样就可能使用X3中较窄的频域序列，通过反卷积和IDFT得到能反映谐波振幅真实变化的时域序列x2。

图3　原始信号及对称增加一倍信号 后组成的新信号的乘积图解 Fig.3 The time domain product process of new sequence

参数识别计算过程用时域和频域曲线示意，图3为原始信号及对称增加一倍信号后组成的新信号的时域乘积过程，图4为对称加长后的新信号对应的频谱。概括起来：截取和对称是为了时域乘积的两个信号周期延拓时避免边界跳跃，同时参与乘积的两个序列DFT后，在频域内避免频谱泄漏，构造符合卷积原理的信号。

图4　对称后的新信号对应的频谱 Fig.4 The frequency domain product process of new sequence

3实验数据应用

式(8)是数字信号DFT普遍的规律，由以上分析可知，不需要对阻尼模型进行假设，便可以还原一个反映谐波振幅变化的时域序列，把识别阻尼的过程概括如下：

(1)实验得到自由衰减振动信号。

(2)依据DFT频谱谱峰粗略确定信号中可能谐波频率，信号分段分别DFT确定各频率谐波的有效长度。

(3)有效长度内对粗略确定的频率计算细化频谱，确定更加精确的频率和初相位。

(4)由频率和初相位情况对信号进行整周期截取后对称增加一倍信号得到新的信号x3(见图3(a))，计算X3(见图4(a))。

(5)x3重新计算细化频谱复核频率和相位，并计算频域序列X1，见图4(c)

(6)由X3和X1可以求解X2(见图4(b))。

(7)对X2进行IDFT得到x2(见图3(b))，取x2的一半即为频率谐波振幅变化的时域序列。

对某钢筋混凝土梁进行脉冲锤击实验，工程实际中噪声是未知的，把安静环境下采集的信号近似当做噪声，冲击响应信号当做真实响应，采样长度4 s，采样点数65 536，其中一点的加速度响应信号和噪声见图5，计算信号的SNR为48 dB。

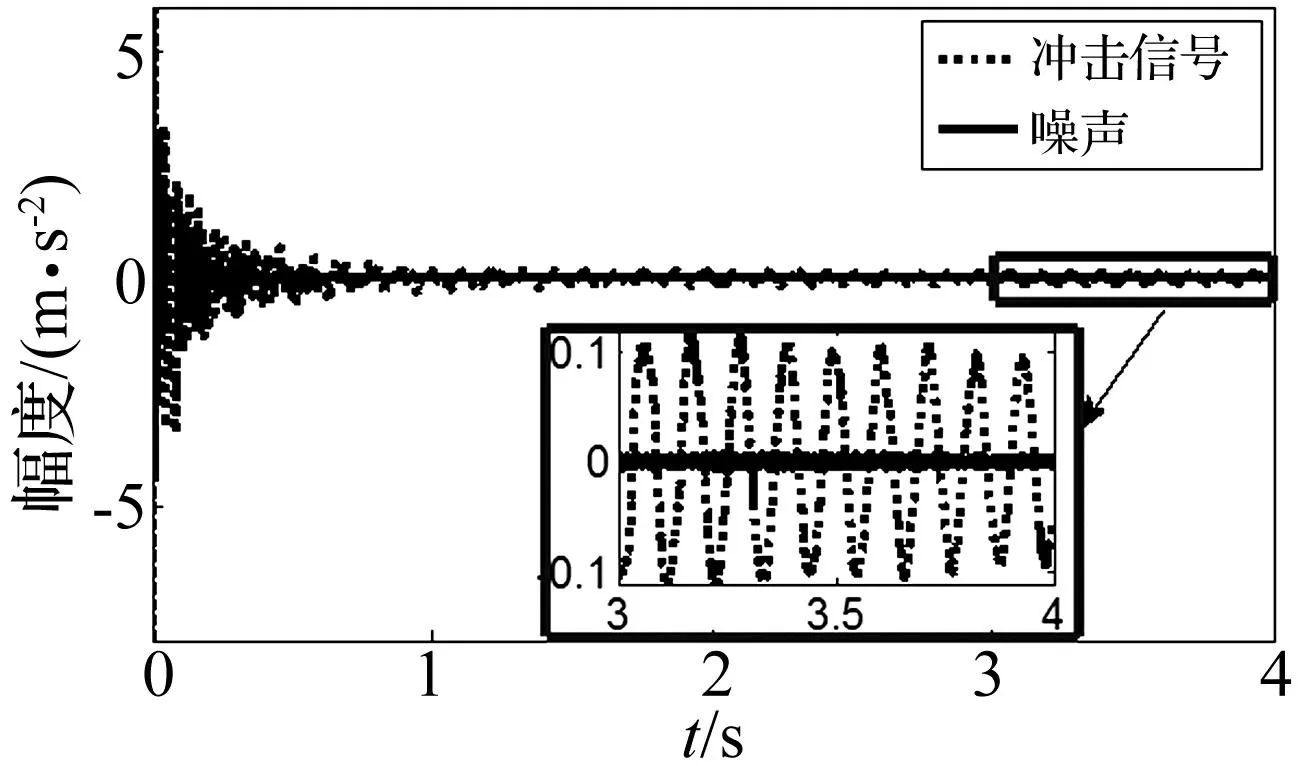
图5　冲击响应信号和噪声 Fig.5 Impulse response signal and noise

把冲击响应信号依次分成4段，分别DFT得到的对应频谱依次为part1,part2,part3,part4，见图6；信号所含谐波的频率大约是：9 Hz, 25 Hz, 34 Hz, 53 Hz, 76 Hz；除基频的有效长度取4 s，其他各频率，由于后三段信号的频谱峰值较小，即HNR较小，有效长度均取1 s。53 Hz附近是密集频率谐波不做分析，对其他4个频率的谐波采用反卷积方法识别得到振幅变化的时域序列，采用取对数后的线性拟合法[20]：

ln(x2(kt))=-ζ2πfkt+lnA

(9)

用自然指数衰减模型来衡量谐波振幅衰减的程度，识别得到阻尼比和振幅值见表1；识别序列和指数拟合见图7，结果表明：实验信号中两个低频谐波的振幅先短时增加到峰值后再衰减，而两个高频谐波的振幅则瞬时达到峰值且整个衰减过程先快后慢。

图6　冲击信号分4段分别DFT的频谱 Fig.6 The spectrum of four segments

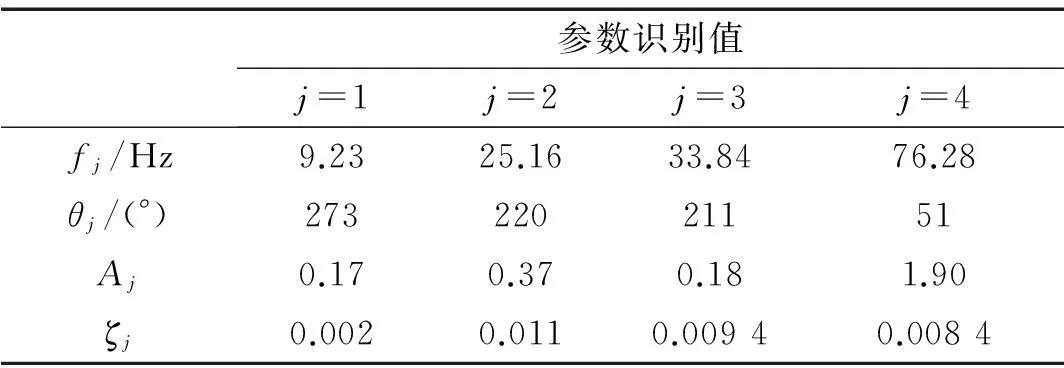
参数识别值j=1j=2j=3j=4fj/Hz9.2325.1633.8476.28θj/(°)27322021151Aj0.170.370.181.90ζj0.0020.0110.00940.0084

图7　实验冲击响应信号的识别序列和指数拟合 Fig.7 Identification decay sequence and pseudo linear fitting in an exponential function for four frequency components

理论上按实验信号峰值两边频谱序列识别阻尼是相同的，而实际会存在差别。频谱间隔较大，幅值较大的频率谐波的识别精度较高，幅值较小的频率易受到周围泄露频谱的影响；一般首选频率间隔较远，远离幅值较大的频率的一边，且与理论频域序列较符合的一边。

4仿真验证

从工程实际采集的信号中识别得到的参数正确与否无从辨识，仿照从实测数据中识别的谐波参数拟定理论谐波参数代入式(1)，采用相同的采样参数，加入30 dB高斯白噪声生成仿真数字信号，用相同的方法和计算过程识别仿真信号的谐波参数和阻尼比，识别得到的时域序列、理论假设衰减曲线和识别序列指数拟合的阻尼比和振幅见图8。理论参数和参数识别值列于表2；理论模拟结果表明：识别的阻尼序列可以真实反映假设阻尼的趋势，而且参数识别值与理论值一致。

各频率频谱混叠程度随各频率间隔和幅值大小而不同，混叠越大对识别结果影响越大，在相对独立幅值较大的频谱中识别的阻尼具有更高的可靠性。

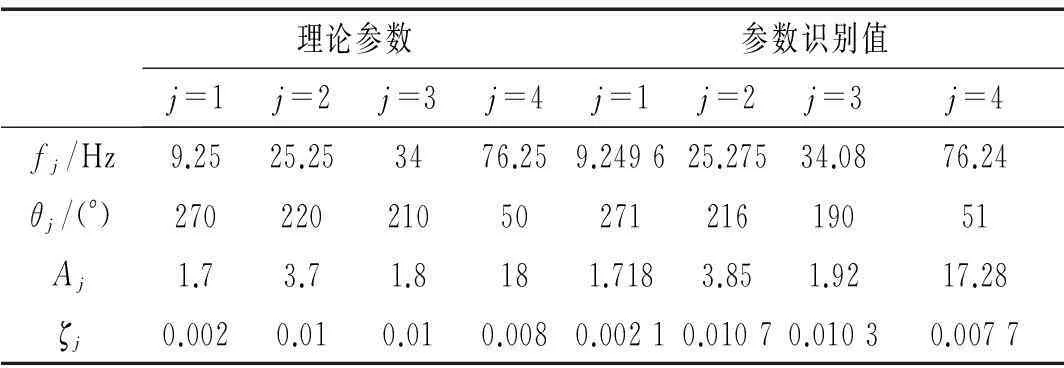
表2　假设信号各频率谐波参数和参数识别值

图8　冲击响应中各频率谐波假设衰减， 识别的衰减序列和序列的指数拟合 Fig.8 The comparison of the exponential assumption, pseudo linear fitting and identification sequence for each frequency component

5结论

本文采用细化频谱方法识别谐波的频率和初相位，分析了冲击响应信号中阻尼比和HNR因素对参数识别的影响，依据DFT卷积和反卷积性质得到谐波振幅变化的时域序列，再用假设模型近似衰减的程度，得到振幅和阻尼比；为研究结构阻尼性质提供更多的有价值信息。仿真模拟验证了本方法的可行性和正确性，对实验信号的分析表明：在实践中的实用性和优越性。具体而言，识别方法对阻尼模型无任何要求，任何形式的振幅变化均可识别；识别得到的谐波振幅随时间变化的时域序列。频域内的密集频谱会影响本方法的识别精度。

参考文献

[1]Yi Wei-jian, Zhou Yun, Kunnath S, et al. Identification of localized frame parameters using higher natural modes [J]. Engineering Stuuctures, 2008, 30(11): 3082-3094.

[2]Neild S A, Williams M S, Mcfadden P D. Nonlinear vibration characteristics of damaged concrete beams[J]. Journal of Structural Engineering, 2003, 129(2): 260-268.

[3]Melhem H, Kim H. Damage detection in concrete by fourier and wavelet analyses [J]. Journal of Engineering Mechanics, 2003, 129(8): 571-577.

[4]Maas S Z, Rbes A, Waldmann D, et al. Damage assessment of concrete structures through dynamic testing methods[J]. Engineering Structures, 2012, 34(1): 351-62.

[5]Ruzzene M, Fasana A, Garibalei L, et al. Natural frequencies and dampings identification using wavelet transform:application to real data[J]. Mechanical Systems and Signal Processing, 1997, 11(2): 207-18.

[6]Kareem A, Gurley K. Damping in structures: its evaluation and treatment of uncertainty [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1996, 59(2-3): 131-57.

[8]Chen G D, Wang Z C. A signal decomposition theorem with Hilbert transform and its application to narrowband time series with closely spaced frequency components [J]. Mechanical Systems and Signal Processing, 2011, 25(2): 1-22.

[9]Bonilha H S, Dawson A E. Creating a mastery experience during the voice evaluation[J]. Journal of Voice, 2012, 1-7.

[10]Yumoto E, Gould W J, Baer T. Harmonics-to-noise ratio as an index of the degree of hoarseness [J]. The Journal of the Acoustical Society of America, 1982, 71(6): 1544-1550.

[11]Papagiannopoulos G A, Beskos D E. On a modal damping identification model for non-classically damped linear building structures subjected to earthquakes[J]. Soil Dynamics and Earthquake Engineering, 2009, 29(3): 583-589.

[12]Sultan C. Proportional damping approximation using the energy gain and simultaneous perturbation stochastic approximation[J]. Mechanical Systems and Signal Processing, 2010, 24(7): 2210-2224.

[13]Adhikari S. Damping models for structural vibration[D]. Cambridge; Trinity College, Cambridge, 2000.

[14]Woodhouse J. Linear damping models for structural vibration [J]. Journal of Sound and Vibration, 1998, 215(3): 547-569.

[15]Kraniauskas P. Transforms in signals and systems [M]. The Great Britain: Addison-Wesley, 1992.

[16]Chopra A K. Dynamics of structures theory and applications to earthquake engineering[M]. 3 ed. London: Prentice Hall, 2006.

[17]Fasana A, Piombo B A D. Identification of linear mechanical systems by deconvolution techniques[J]. Mechanical Systems and Signal Processing, 1997, 11(3): 351-373.

[18]Oppenheim A V, Schafer R W. Discrete-time signal processing [M]. 3 ed. London: Prentice Hall, 2009.

[20]Staszewski W J. Identification of damping in MDOF systems using time-scale decomposition[J]. Journal of Sound and Vibration, 1997, 203(2): 283-305.