一种基于非对称窗的相位差法

第一作者罗久飞男，博士生，1987年生

通信作者谢志江男，教授，博士生导师，1963年生

一种基于非对称窗的相位差法

罗久飞，谢志江，熊鹰

(重庆大学机械工程学院，重庆400044)

摘要：提出一种新的相位差法，用来校正离散频谱中频率、相位和幅值的误差。由于经典窗函数的对称性，它们具有恒定的时延和相同的相位响应。解除窗函数的对称性限制，可以引入具有可变时延和不同相位响应的非对称窗函数。建立在非对称窗的可变相位基础之上的相位差法可以克服传统方法的一些固有缺点。仿真表明通过选择合适的窗函数，对相邻很近的频率成分，该方法校正也能保证精确的结果。该方法还可以从根本上避免最高谱线定位错误带来的误差。对带有加性高斯白噪声的理论信号分析，结果显示直接基于非对称窗的校正方法与传统方法的抗噪性能相似。另外，将传统方法中的对称窗替换为非对称窗可以提高算法的抗噪性能。

关键词：窗函数；线性相位；频谱校正；相位差法

收稿日期：2014-05-07修改稿收到日期：2014-08-14

中图分类号:TN911.6文献标志码：A

Phase difference method based on asymmetrical windows

LUOJiu-fei,XIEZhi-jiang,XIONGYing(School of Mechanical Engineering, Chongqing University, Chongqing 400044, China)

Abstract:An improved method, phase difference method based on asymmetric windows, was proposed aiming at correcting the errors of parameters in discrete spectrum. Several examples simulations show that with proper choice of asymmetric windows, the new method can correct the errors of frequency components located in less than five DFT bins. And it can also avoid the errors induced by the mistaken location of right spectral line. The corrected results of a theoretical signal involved in different noise conditions also exhibit a stronger robustness against additive noise when the symmetric windows are replaced with asymmetric windows.

Key words:windows function; Linear phase; spectrum correction; phase difference

在离散频谱分析中，由于无法整周期截断信号以及有限的观测时间，不可避免地引入频谱的泄露和栅栏效应，常常导致频率成分的频率、振幅和相位存在一定的误差。加窗技术可以在一定程度上减轻这种缺陷，但不能彻底地解决。例如，对加矩形窗和汉宁窗的单谐波进行分析，其振幅的最大误差分别可达36.4%和15.3%[1-2]。对于任何类型的窗函数，最大频率误差是其频率分辨率的1/2[2]。而最大的相位误差甚至高达±90度[3-4]。毫无疑问，解决离散频谱中的误差问题在实际的工程应用中具有重大意义。因此，近几十年里国内外提出了许多频谱校正方法，通常可分为四类，即插值法、FT连续变焦法、能量重心法和相位差法。

插值法是目前研究得最多的校正法，并且在很多工程问题中得到应用。该方法的主要思想是通过若干已知谱线的加权比值来得到信号的精确频率，因此又叫比值法。目前，已经衍生出多种不同的算法[6-18]。FT连续变焦法也被称为搜索法，通过反复使用离散傅里叶变换搜索出临近区域的最高谱线，来获得信号的精确频率。这种算法易于理解和实施，但是计算量相对较大[19-21]。Offelli等[22]首先提出了基于能量重心的校正方法。丁康等[23]证明了对称窗函数功率谱的能量重心都在坐标原点或原点附近。该定理不但奠定了能量重心法的理论基础，而且使得能量重心校正方法成为适用于不同窗函数的一种统一方法。近年来，算法的理论误差，频率成分间的干扰以及宽带噪声等各种影响因素得到了进一步的研究[24-27]。李慧兵等系统地比较了能量重心法和其他几种方法。

第四类是相位差法。这种方法最初是由McMahon等[28]提出作为相位插值工具来估计带噪声的单频信号的频率。朱利民等[29-30]进一步改进了这种方法。谢明等[31]通过研究两个连续的时域信号，提出了基于时移(MBTS)的相位差校正法的一种特例。丁康等[32]推导出了通用的基于时移的相位差校正法。黄云志[33]提出了另一种新型的基于窗中心移动的相位差法(MBTWC)。同时，丁康等[34]提出了综合法，它包含了信号的时移和信号长度改变。2002年，朱利民等[35]深入研究了噪声对该方法的影响。研究结果表明，相位差法在随机噪声的条件下，显示出更高的稳定性。

然而，目前的相位差法都是建立在对称窗函数的基础之上的。在离散频谱法中尚未提及非对称窗函数的使用。因此，本文提出了基于非对称窗函数的新相位差法(MBAW)来修正离散频谱中频率、振幅和相位误差。通过数值计算，证实了该方法的有效性，并将其与传统基于对称窗函数的相位差法进行了比较。仿真结果表明，通过选择恰当的窗函数，新方法对相邻较近的频率成分也可以取得较好的校正结果。在加性噪声下，新方法与传统方法抗噪性能相似，进一步将传统方法中对称窗函数替换为非对称函数，可加强其抗噪性能。另外，新方法从根本上避免了目前算法中谱线定位错误而带来的误差。这使得基于非对称窗函数的相位差法在某些工程应用当中更具有优势。

1非对称窗函数的频谱特性

目前，所有的经典窗函数都是时间对称的，它们设计简单并具有线性相位。然而它们也有潜在不足，例如恒定时延和某些频率响应的限制。解除对称性的限定则可以构造出具有特殊用途的非对称窗[36-38]。由于对称性和因果性时移，经典窗具有相同的相位谱。对于非对称窗则能够拥有完全不同的相位响应。

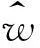
为方便描述，将这种非对称窗函数称为L-U-汉宁窗，其时域逆形式称为L-D-汉宁窗。这二者构成一对非对称窗函数。同样，还可以衍生出其他一系列非对称窗，例如L-U-最小三项窗(见图2)。

进一步定义核瓣这一概念，其表示位于主瓣中心且占有两个频率分辨率的宽度的区域。观察以上非对称窗函数的频谱特性，容易得出如下几个结论。①非对称窗的“主瓣”比相应的对称窗的主瓣略宽一点。非对称窗“旁瓣”不明显，它与相应的对称窗旁瓣的包络线很相近，具有近似的衰减速度。因此，二者的幅值特性非常相似。②对称窗的相位始终是线性的，而非对称窗的相位是非线性，但在核瓣内近似线性。③由于任何窗函数(对称或者非对称)在主瓣中心的相位都为零，因此构造出的非对称窗与其相应的对称窗相位线必定会交于主瓣中心。这些结论给基于非对称窗函数的相位差法提供了理论基础。

(a)　汉宁窗和L-U-汉宁窗 　(b)　归一化幅值响应 (c)　归一化相位响应 图1　非对称窗函数特性 Fig.1 Characteristics of the asymmetric window

(a)　最小三项窗和L-U-最小三项窗 (b)　归一化幅值响应 (c)　归一化相位响应 图2　非对称窗函数特性 Fig.2 Characteristics of the asymmetric window

2校正法理论

为了推导基于非对称函数的相位差法校正理论，我们考虑如下单一的余弦信号

x(t)=Acos(2πf0t+θ)

(1)

式中：A为振幅，f0为精确频率，θ为初相位。它的傅里叶变换是：

X(f)=0.5Aejθδ(f-f0)+0.5Ae-jθδ(f+f0)

(2)

该余弦信号被长度为T的窗函数wT(t)截断。假设该窗wT(t)的傅里叶变换为|WT(f)|ejφ(f)。根据卷积定理，加窗信号x(t)wT(t)的频谱为X(f)*|WT(f)|ejφ(f)。考虑

正频率部分，可得

这里忽略了来自负频率的的干扰，因为它只有在某些极端的情况下才会对正频率有较大干扰。此时相位可以表示为φ( f )=θ-φ( f- f0)。在DFT中，设点数为N，采样频率为fs，这样频率分辨率为fΔ=fs/N。根据DFT的定义，频率归一化后的相位可以写为：

φ(k-k0)=φ(k)-θ

(3)

式中：k代表离散频谱中频率采样的序号，且有k0=f0/fΔ。需要说明的是，k的取值不但可以是整数也可以通过插值方式取值为小数。

根据式(3)，对于加两个不同窗函数(至少一个为非对称窗函数)的同一段信号，可以得到

φ1(k-k0)=φ1(k)-θ

(4)

φ2(k-k0)=φ2(k)-θ

(5)

二式相减消掉θ，则归一化频率与相位差之间的关系如式(6)所示

μ(k)=Δφ(k)=φ2(k)-φ1(k)=

φ2(k-k0)-φ1(k-k0)

(6)

基于对称窗的相位差法利用了线性相位特征来得到归一化校正值Δk。显然，此时由于非对称窗的非线性相位的原因，Δk和相位差之间的线性关系不复存在。但有一点非常重要，已经在前文中指出，非对称窗函数与其相应的对称窗函数相位线必定会交于主瓣中心。这有助于我们找出理论精确的频率，即

μ(k0)=Δφ(k0)=φ2(k0)-φ1(k0)=

φ2(0)-φ1(0)=0

(7)

式(7)表明当给定频率值等于精确频率值时二者相位差为零，即信号的精确频率k0是μ(k)=0的一个解。

定理1若μ(k)的一阶导数存在，且当k∈[kob-1/2,kob+1/2]时，恒有μ′(k)>0或μ′(k)<0，那么对于给定的归一化频率k*(kob-1/2≤k*≤kob+1/2)只要满足μ(k*)=0就有k*=k0，相应信号的精确频率为f=k0fΔ，其中kob为观测频率的谱线号。

证明：由于kob为观测频率的谱线号，则可知归一化的精确频率k0必定在[kob-1/2,kob+1/2]范围内，这就确定了其存在性，且有μ(k0)=0。若给定的归一化频率k*(kob-1/2≤k*≤kob+1/2)满足μ(k*)=0且k*≠k0，那么根据罗尔定理在k0与k*之间必定有一个值ko得μ′(ko)=0。显然，这与前提条件矛盾。因此，必定有k*=k0成立。

定理的几何解释为在观察频率附近的相位线交点的横坐标正是该信号精确频率，纵坐标为精确的初相位。显然，窗中心移动法是它地特例，此时观测频率对应的相位差Δφ(kob)与校正值Δk之间具有良好的线性关系。恰当的选择非对称窗函数(或者一个对称窗函数和一个非对称窗函数)，定理1的条件很容易满足。因此，基于非对称窗函数的频率校正问题转化为在k∈[kob-1/2,kob+1/2]中求解方程μ(k)=0的问题。由于很难求得该方程的解析解，这就变成了一个经典的数值求解问题。在每一步求解过程中，φ1(k)和φ2(k)很容易通过单点DFT方法得到。

目前有许多种求根算法来逼近方程的根，最简单的算法是二分法。它可靠且易于实现，然而它收敛缓慢。牛顿法收敛更快，但需要计算导数，计算量大。利用非线性窗函数的相位线近似直线的性质，采用割线法只需简单几步迭代就可快速收敛到根。之后，将k0代入加对称窗后的数据进行单点离散傅里叶变换得到变换后的实部和虚部分别是：

(8)

(9)

精确的相位和幅值可以通过式(10)和式(11)算出，

θ=φ(k0)=arctan[AI(k0)/AR(k0)]

(10)

(11)

式中：CG表示相应窗函数的相干增益。

除此之外，将传统方法中的对称窗函数替换为非对称窗函数还可以衍生出多种基于非对称窗函数校正方法。

3仿真计算及其结果

这部分给出一些仿真算例来验证基于非对称窗函数相位差方法的有效性，并与传统的方法做一些比较。为了方便地观察和比较不同算法的效果，约定采样频率为1 024 Hz，数据总长度为1 024点。在MBTS中，选择前512个点作第一段，剩下的512点为作第二段。在MBTWC中，将原始数据后半部分置零作第一段，前半部分置零作第二段。所加窗函数都包含512点。在MBAW中，原始数据加1 024点的对称窗作第一段，加具有同样长度的非对称窗作第二段。

3.1无噪声理论信号

3.1.1相隔较远的频率成分校正结果

仿真信号由式(12)产生，它包含有三个谐波分量，其中f1=253.3 Hz和f2=262.6 Hz相对接近，第三个谐波分量f3=330.7 Hz，与f1、f2相隔较远。

Y=cos(2π253.3t+π/4)+cos(2π262.6t+π/6)+

cos(2π330.7t-π/2)

(12)

为了评估这些方法对不同的归一化频率误差的有效性，考虑不同的f3的值，范围从330.5 Hz到331.5 Hz步距为0.05 Hz。在MBTS和MBTWC中数据加汉宁窗。在MBAW中，第一段和第二段的数据分别加汉宁窗和L-U-汉宁窗。图3～图13显示了三种频率成分经各种校正方法校正后的频率、幅值和相位与理论值的误差。

图3 校正后的f1频率与理论值的误差(随着f3频率的改变)Fig.3Frequencyerrorsoff1withdifferentvaluesoff3图4 校正后的f1幅值与理论值的误差(随着f3频率的改变)Fig.4Amplitudeerrorsoff1withdifferentvaluesoff3图5 校正后的f1相位与理论值的误差(随着f3频率的改变)Fig.5 Phaseerrorsoff1withdifferentvaluesoff3

图6 校正后的f2频率与理论值的误差(随着f3频率的改变)Fig.6Frequencyerrorsoff2withdifferentvaluesoff3图7 校正后的f2幅值与理论值的误差(随着f3频率的改变)Fig.7Amplitudeerrorsoff2withdifferentvaluesoff3图8 校正后的f2相位与理论值的误差(随着f3频率的改变)Fig.8 Phaseerrorsoff2withdifferentvaluesoff3

图9 校正后的f3频率与理论值的误差Fig.9 Frequencyerrorsofcorrectedf3图10 校正后的f3幅值与理论值的误差Fig.10Amplitudeerrorsofcorrectedf3图11 校正后的f3相位与理论值的误差Fig.11Phaseerrorsofcorrectedf3

如图所示，f3的频率变化对f1和f2的校正影响很小。因为随着f3变化，f1和f2频率误差接近直线，然而基于不同方法的校正结果差异是很明显的。所有提出的这些方法都能取得较高精度的校正结果。频率校正误差f1、f2低于0.002频率分辨率，f3低于0.000 01频率分辨率。f1、f2的幅值误差小于于0.000 3，f3小于0.000 002。相位校正误差f1、f2低于0.3°，f3低于0.001°。f3的校正误差比f1、f2低很多的原因是f3与它们相隔较远，受二者旁瓣的干扰较小的缘故。仿真结果表明本文提出的校正方法是有效的。用它校正后的频率、幅值和相位与理论值的误差能达到与传统方法一样的精确度。鉴于幅值和相位都是通过校正后频率来计算的，在接下来的实验中仅仅比较频率校正的结果。

3.1.2临近的频率成分校正结果

在校正方法中最重要的参数之一是两频率成分之间的距离大小。当频率成分愈加接近时，来自对方的干扰就愈加严重。当两频率成分足够接近时，干扰对校正方法性能的影响是非常大的。因此，我们考虑f1逐渐接近f2，步距为0.1Hz，且分别对f1，f2的相位进行扫描，选择最大的误差作为一次步距的结果。图12、图13显示使用三种校正方法校正后，f1和f2与理论值误差，Δλ表示f1和f2频率的间距。在MBTS和MBTWC中窗函数为最小三项窗，在MBAW中窗函数为最小三项窗的和L-U-最小三项窗。选择最小三项窗是因为其第一旁边很低且主瓣较窄。总的来看，两频率间距变小时，校正误差增大。而新方法可以像校正相隔较远的谱线一样精确地校正相隔很近(大于3个频率分辨率)的谱线。

仿真结果表明新方法对相隔较近的频率成分也能取得较好的校正结果。即使频率间隔仅为3个频率分辨率左右，校正频率误差也很稳定且不超过0.01频率分辨率。这种方法突破了传统方法中为了取得较高精度的校正结果要求频率间距大于5个频率分辨率的限制。在新方法中相位差可以仅仅通过对同一段数据加不同的窗函数得到，并不改变窗函数的长度。而在MBTS和MBTWC中，整个数据被分成两部分，相应的窗函数长度也变短。因此，对同样长度的数据，所使用的窗长并不相同，非对称窗具有更窄的主瓣。传统方法中窗函数主瓣扩张使得相邻频谱成分之间干扰增大，甚至产生主瓣干涉。所以，新方法更适合校正相邻较近的频率成分。

3.2带白噪声的理论信号仿真

带有加性高斯白噪声的理论信号由(13)给出

Ye(t)=cos(2π227.3t+π/2)+e(t)

(13)

式中，包含一个频率为227.3 Hz的单频信号，e(t)是具有高斯分布的白噪声。由于噪声的随机性，每次校正的结果略有不同。在同一信噪比下，考察共计10 000次的独立实验，用其均方根值来评估这几种方法。在图中关于均方根值评价的指标(IRMSE)定义如下

IRMSE=-20lgRMSE

(14)

其中

(15)

式(15)中,Ntr代表实验次数,fi是在噪声情况下每次的校正结果,f0表示理论频率。对于单谐波，信噪比定义为

SNR=10lg[A2/(2σ2)]

(16)

其中：A为谐波信号的幅值，σ2为噪声的方差。仿真中使用的窗函数分别为汉宁窗和L-U-汉宁窗。

图14显示了不同SNR下三种算法的仿真结果。总体上IRMSE随着SNR增大而稳步上升。MBTS, MBTWC以及MBAW没有明显区别。这表明三者的抗噪声能力基本一致，其中MBTWC比MBAW，MBTS略好。

图12 不同Δλ的f1校正频率误差(最小三项窗)Fig.12Frequencyerrorsofcorrectedf1withdifferentvaluesofΔλ图13 不同Δλ的f2校正频率误差(最小三项窗)Fig.13Frequencyerrorsofcorrectedf2withdifferentvaluesofΔλ图14 1000段信号的IRMSE(MBAW)Fig.14IRMSEforf1with10000independenttrials(MBAW)

将MBTWC中窗函数替换为非对称窗函数可以改善MBTWC的抗噪能力(见图15)。仿真信号与图14中完全一致的，在改进方法中，将第一段和第二段信号所加的汉宁窗替换为L-D-汉宁窗和L-U-汉宁窗，长度相同。在所有的信噪比情况下，MBTWC&AW的IRMSE指标都比MBTWC和MBTS大。这表明改进后的算法对加性随机噪声的抗性更强。

3.3谱线错误定位的影响

在3.2中并未考虑谱线错误定位的影响，我们始终选择正确的谱线来校正。然而，由于噪声对理论信号的干扰，在实际工程中总是选用最高的谱线来校正，却并不能保证它是应该被用来校正的正确的谱线。特别是当信噪比很大的时候或者当真实信号靠近两条谱线的中间位置的时候，谱线定位错误将给频率校正带来很大的误差[21]。

图16～图17显示了不同校正方法，谱线定位错误的数目。对于不同等级的噪声和不同的频率偏差，进行10 000次独立试验，考察其谱线定位错误的数目。总的来看，错误定位的数目随着理论频率靠近两谱线中间区域而增加。对于同一频率而言，谱线定位错误的百分比随着SNR增加而减少。可以看出，当理论频率接近两谱线中间区域或信噪比很大的时候错误定位的现象非常严重。如果考虑到谱线定位错误，MBTWC和MBTS校正的结果会更差。然而，新方法从根本上避免了这个问题，这是因为新算法对错误定位谱线不敏感。即使选错了谱线，根据迭代算法仍然可以逼近相位零点，从而得到真实频率，其结果与选取的谱线号无关。这使得新方法在大噪声下更加稳健。

图15 1000段信号的IRMSE(MBTWC&AW)Fig.15IRMSEforf1with10000independenttrials(MBTWC&AW)图16 10000段信号中谱线定位错误的数量百分比(MBTWC)Fig.16 PercentageofmistakenlocationofthefirstsegmentinMBAWof10000independenttrials图17 1000段信号中谱线定位错误的数量百分比(MBTS)Fig.17 PercentageofmistakenlocationofthesecondsegmentinMBAWof10000independenttrials

4结论

本文提出了一种新的相位差法来校正离散频谱中频率、相位和幅值的误差。第一次将非对称窗函数引入离散频谱校正之中。研究了基于截断法构造出的非对称窗的幅值和相位特性。推导了基于非对称窗函数的相位差法理论。在新方法中，先通过数值方法来逼近理论频率，然后再通过单点的离散傅里叶变换来求得精确的相位和幅值。给出了不同于传统相位差法的频率、相位和幅值校正公式。新算法的计算量有所增加，但是在目前的计算机运算速度下，完全可以忽略不计。

仿真结果表明本文提出方法可以仅仅通过对同一段数据加非对称窗(或者一个对称窗和一个非对称窗)而实现对频率、相位和幅值的校正，精度与传统方法一致。选择恰当的窗函数，对相邻较近的频率成分也可以取得较好的校正结果，这是传统方法的盲区。在加性噪声下，新方法与传统方法性能相似。将传统方法中对称窗函数替换为非对称函数，改进的方法具有更强的抗噪声能力。另外，新方法从根本上避免了最高谱线定位错误而引入的误差。因此，在工程环境下与传统方法相比新方法稳健性更高，更适合于工程应用。虽然该方法对于较为密集分布的频率成分取得较好的效果，但是对于过于密集的频率成分(出现主瓣干涉)，仍然会产生相当大的误差。密集频谱校正是目前校正方法的难点之一[39], 有待进一步研究。

参考文献

[1]Ming X, Kang D. Corrections for frequency, amplitude and phase in a fast fourier transform of a harmonic signal [J]. Mechanical Systems and Signal Processing,1996,10(2): 211-221.

[2]丁康，谢明.离散频谱三点卷积幅值修正法的误差分析[J].振动工程学报，1996,9(1): 92-98.

DING Kang, XIE Ming. Error analysis for amplitude correction method using convolution of three points in discrete spectrum[J].Journal of Vibration Engineering, 1996,1(9): 92-98.

[3]Kang D, Ming X, Xiaofei Z. Phase difference correction method for phase and frequency in spectral analysis [J]. Mechanical Systems and Signal Processing,2000,14(5): 835-843.

[4]Dishan H. Phase error in fast fourier transform analysis [J]. Mechanical Systems and Signal Processing,1995,9(2): 113-118.

[5]Rife D C, Vincent G. Use of the discrete Fourier transform in the measurement of frequencies and levels of tones [J]. Bell Syst Tech J,1970,49(2):197-228.

[6]Jain V K, Collins W L, Davis D C. High-accuracy analog measurements via interpolated FFT [J]. Instrumentation and Measurement, IEEE Transactions on,1979,28(2):113-122.

[7]Grandke T. Interpolation algorithms for discrete Fourier transforms of weighted signals [J]. Instrumentation and Measurement, IEEE Transactions on,1983,32(2):350-355.

[8]Narduzzi C, Offelli C. Real-time high accuracy measurement of multifrequency waveforms [J]. Instrumentation and Measurement, IEEE Transactions on,1987,1001(4):964-970.

[9]Andria G, Savino M, Trotta A. Windows and interpolation algorithms to improve electrical measurement accuracy [J]. Instrumentation and Measurement, IEEE Transactions on,1989,38(4):856-863.

[10]Schoukens J, Pintelon R, Van Hamme H. The interpolated fast Fourier transform: a comparative study [J]. Instrumentation and Measurement, IEEE Transactions on,1992,41(2):226-232.

[11]Offelli C, Petri D. The influence of windowing on the accuracy of multifrequency signal parameter estimation [J]. Instrumentation and Measurement, IEEE Transactions on,1992,41(2):256-261.

[12]Belega D, Dallet D. Multifrequency signal analysis by Interpolated DFT method with maximum sidelobe decay windows [J]. Measurement,2009,42(3):420-426.

[13]Aboutanios E, Mulgrew B. Iterative frequency estimation by interpolation on Fourier coefficients [J]. Signal Processing, IEEE Transactions on,2005,53(4):1237-1242.

[14]Belega D, Dallet D, Petri D. Statistical description of the sine-wave frequency estimator provided by the interpolated DFT method [J]. Measurement,2012,45(1):109-117.

[15]Borkowski J, Mroczka J. LIDFT method with classic data windows and zero padding in multifrequency signal analysis [J]. Measurement,2010,43(10):1595-1602.

[16]Belega D, Dallet D, Petri D. Accuracy of sine wave frequency estimation by multipoint interpolated DFT approach [J]. Instrumentation and Measurement, IEEE Transactions on,2010,59(11):2808-2815.

[17]Belega D, Dallet D. Amplitude estimation by a multipoint interpolated DFT approach [J]. Instrumentation and Measurement, IEEE Transactions on,2009,58(5):1316-1323.

[18]Duda K. DFT interpolation algorithm for kaiser-bessel and dolph-chebyshev windows [J]. Instrumentation and Measurement, IEEE Transactions on,2011,60(3):784-790.

[19]刘进明，应怀樵.FFT谱连续细化分析的富里叶变换法[J].振动工程学报，1995,8(2):162-166.

LIU Jin-ming, YING Huai-qiao. Zoom FFT spectrum by fourier transform [J]. Journal of Vibration Engineering, 1995,8(2): 162-166.

[20]陈奎孚，焦群英，高小榕.提高FF谱质量的一种新方法[J].振动、测试与诊断，1998,18(2):216-220.

CHEN Kui-fu,JIAO Qun-ying,GAO Xiao-rong. A new approach to the improvement of FFT spectrum qual itity [J]. Journal of Vibration, Measurement & Diagnosis,1998,18(2):216-220.

[21]丁康，谢明，杨志坚.离散频谱分析校正理论与技术[M].北京：科学出版社，2008.

[22]Offelli C, Petri D. A frequency-domain procedure for accurate real-time signal parameter measurement [J]. Instrumentation and Measurement, IEEE Transactions on,1990,39(2):363-368.

[23]丁康，江利旗.离散频谱的能量重心校正法[J].振动工程学报，2001,14(3):354-358.

DING Kang, JIANG Li-qi. Energy centrobaric correction method for discrete spectrum [J]. Journal of Vibration Engineering,2001,14(3):354-358.

[24]丁康，郑春松，杨志坚.离散频谱能量重心法频率校正精度分析及改进[J].机械工程学报，2010,46(5):43-48.

DING Kang, ZHENG Chun-song, YANG Zhi-jian. Frequency estimation accuracy analysis and improvement of energy barycenter correction method for discrete spectrum [J]. Journal of Mechanical Engineering, 2010,46(5):43-48.

[25]Belega D, Dallet D, Petri D. Accuracy of the normalized frequency estimation of a discrete-time sine-wave by the energy-based method [J]. Instrumentation and Measurement, IEEE Transactions on, 2012,61(1):111-121.

[26]Huibin L, Kang D. Energy based signal parameter estimation method and a comparative study of different frequency estimators [J]. Mechanical Systems and Signal Processing,2011,25(1):452-464.

[27]丁康，林慧斌.离散频谱四点能量重心校正法及抗噪性能分析[J].振动工程学报，2009,22(6):659-664.

DING Kang, LIN Hui-bing. Anti-noise performance of energy centrobaric correction method using four points for discrete spectrum[J].Journal of Vibgration Engineering,2009,22(6): 659-664.

[28]McMahon D, Barrett R. An efficient method for the estimation of the frequency of a single tone in noise from the phases of discrete fourier transforms [J]. Signal Processing,1986,11(2):169-177.

[29]朱利民，贾民平，钟秉林.转子振动监测中的采样与相位误差补偿[J].东南大学学报，1997,27(2):115-120.

ZHU Li-min, JIA Min-ping,ZHONG Bing-ling. Sampling and phase error compensation methods in rotor vibration monitoring [J]. Journal of Southeast University,1997, 27(2):115-120.

[30]Santamaria I, Pantaleon C, Ibanez J. A comparative study of high-accuracy frequency estimation methods [J]. Mechanical Systems and Signal Processing,2000,14(5):819-834.

[31]谢明，张晓飞，丁康.频谱分析中用于相位和频率校正的相位差校正法[J]. 振动工程学报，1999，12(4):444-459.

XIE Ming,ZHANG Xiao-fei,DING Kang. A phase difference correction method for phase and frequency correction in spectral analysis [J]. Journal of Vibration Engineering,1999,12(4): 444-459.

[32]丁康，钟舜聪.通用的离散频谱相位差校正方法[J]. 电子学报，2003,31(1):142-145.

DING Kang, ZHONG Shun-cong. A universal phase difference correcting methods on discrete spectrum [J]. Acta Electronica Sinica,2003,31(1):142-145.

[33]黄云志，徐科军.基于相位差的频谱校正方法的研究[J]. 振动与冲击，2005,24(2):77-79.

HUANG Yun-zhi, XU Ke-jun. Study on the spectrum correcting method based on phase difference [J]. Journal of Vibration and Shock,2005,24(2):77-79.

[34]丁康，朱小勇，谢明，等.离散频谱综合相位差校正法[J].振动工程学报，2002,15(1):114-117.

Ding Kang, Zhu Xiao-yong, Xie Ming, et al. Synthesized correcting method of phase difference on discrete spectrum [J]. Journal of Vibration Engineering,2002,15(1):114-117.

[35]Zhu L M, Li H X, Ding H, et al. Noise influence on estimation of signal parameter from the phase difference of discrete fourier transforms [J]. Mechanical Systems and Signal Processing, 2002,16:991-1004.

[36]Florencio D A. On the use of asymmetric windows for reducing the time delay in real-time spectral analysis [C]. Acoustics, Speech, and Signal Processing, 1991 ICASSP-91. 1991 International Conference on, 1991: IEEE.

[37]Zivanovic M, Carlosena A. On asymmetric analysis windows for detection of closely spaced signal components [J]. Mechanical Systems and Signal Processing,2006,20(3): 702-717.

[38]Shannon B J, Paliwal K K. Feature extraction from higher-lag autocorrelation coefficients for robust speech recognition [J]. Speech Communication,2006,48(11):1458-1485.

[39]霍兵勇，易伟建.密集频率数字信号的判定和校正方法[J].振动与冲击,2013,32(2):171-174.

HUO Bing-yong,YI Wei-jian.Identification and correction for a digital signal with close frequencies[J]. Journal of Vibration and Shock,2013,32(2):171-174.