一种柴油机机脚螺栓连接结构冲击极限载荷快速计算方法

第一作者高霄汉男，博士生，1974年生

一种柴油机机脚螺栓连接结构冲击极限载荷快速计算方法

高霄汉1，汪玉2，杜志鹏3，杜检业3

(1.海军工程大学, 武汉430033； 2.解放军92857部队,北京100161; 3. 解放军92537部队，北京100161)

摘要：把柴油机机脚螺栓连接简化为双弹簧模型，将其与设备一起简化为单自由度系统，结合等效弹簧的柔度曲线规律，设定了机脚螺栓连接的冲击失效判据，并建立了系统的冲击动力学方程。在这一过程中找到了一种快速判断机脚螺栓连接抗冲击性能的方法。

关键词：螺栓；双弹簧系统；冲击；结合面分离

基金项目：国家自然科学基金(51209215)

收稿日期：2014-07-04修改稿收到日期：2014-08-19

中图分类号:O347.3文献标志码：A

Fast computation method for limit shock load of engine bracket bolts

GAOXiao-han1,WANGYu2,DUZhi-peng3,DUJian-ye3(1. Naval University of Engineering, Wuhan 430033, China;2. Unit 92857 of PLA, Beijing 100161, China; 3. Unit 92537 of PLA, Beijing 100161, China)

Abstract:A double-spring model for bolted joints was introduced as the model of engine bracket bolts and the system integrating the equipment and the bolted joints was considered as a one degree of freedom system. Taking into account the effect of interface opening on the elastic behavior of bolted joints, a disabling criterion for bolted joints under impact load was proposed. The dynamics equation of the system was built and a fast computation method for the limit shock load of engine bracket bolts was presented.

Key words:bolt; double-spring model; impact; interface opening

众所周知，水下非接触爆炸会对船舶设备造成严重破坏[1]。而大型设备中的某些连接件，如柴油机机脚螺栓，承受的冲击载荷会更大，属结构中薄弱环节，需特别关注。目前国内对于船舶设备抗冲击研究，主要采取冲击实验校核方法，而对其抗冲击能力没有定量的认识。基于此，国内在研究设备抗冲击的过程中引入了冲击极限载荷的概念。其定义为在冲击作用及其后过程中，船用设备功能具有一定的可用性，其冲击响应(应力、变形、配合等)达到最大允许值所对应的虚拟理论载荷。冯麟涵[2]即采用设计冲击谱(Ds，Vs，As)来描述这一概念，并采用时域法建立设备精确有限元模型，逐渐增强冲击环境，求解转换后的时间历程冲击载荷作用下的设备响应，得到设备冲击响应所对应的设备毁损的最小冲击输入。计晨等[3]也采用了类似方法得到了某齿轮箱的冲击极限载荷。显然上述方法耗费的工作量很大。而用上述方法来获取机脚螺栓连接结构的冲击极限载荷并不适宜。一方面是因为很难在多体动力学模型中准确模拟这类连接件的传递特性，另一方面，机脚螺栓连接体量相对柴油机而言较小，如用上述方法则会导致网格数量较大，使得多体动力学计算模型较大，影响计算速度，甚至在某些刚柔混合建模情况下，这种大刚度梯度使得计算难于顺利进行。而如果仅考量机脚螺栓连接结构本身的抗冲击情况，上述方法显然也将问题复杂化了。本文即是针对这一问题，综合国内外对螺栓连接系统抗冲击研究，将机脚螺栓连接结构简化为双弹簧系统，将机脚螺栓连接结构及其上的柴油机模块简化为单自由度系统，结合双弹簧系统柔度特性曲线规律，建立单自由度系统的冲击动力学方程，并找到了一种快速计算其冲击极限载荷的方法。从而避免了繁琐的多体动力学及螺纹连接建模过程。

1螺栓连接结构的模型

由于机脚螺栓连接所处位置特殊，它对柴油机整机的动力学特性也有较大影响，因此除需考虑抗冲击要求外，还需考虑抗疲劳、防松等多种要求[4]。这些要求必须在螺栓连接模型中加以体现。目前螺栓在研究中多以弹簧-阻尼单元或梁单元作等效替代，该方法使计算量骤减，但要找到一种能准确描述螺纹连接内在特性，特别是其非线性特性的等效模型是非常困难的。国内外许多学者在这方面都做了大量研究[5-6]，本文采用的是德国VDI2230-2003高强度螺纹连接系统计算指南的双弹簧模型，其原理为将螺栓连接简化为双弹簧系统(见图1)，模型中螺纹受拉，用拉伸弹簧表示，被连接件受压，用压缩弹簧表示，模型中考虑了预紧力，这样就考虑了螺纹连接的抗疲劳及防松要求了。根据机脚螺栓的实际装配、预紧及受载情况，将其归属于偏心夹持、偏心加载的螺栓。则模型组合柔度公式为：

(1)

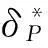
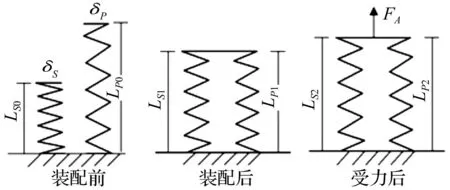
图1　预紧螺纹连接结构等效弹簧模型 Fig.1 Equivalent spring model of preloaded bolted joint

图2　机脚模型 Fig.2 Model of the engine bracket

为方便对照，选取某一柴油机机脚螺栓强度校核模型算例，设该柴油机总重约1t，设备底部共有4个机脚，每个机脚通过4个螺钉连接到机体上，通过一个螺栓固定在柴油机安装支座上。机脚模型见图2。在水下非接触爆炸时，机脚螺栓首先承受基础传来的冲击载荷，属机构中的薄弱环节，且每个机脚此类螺栓仅有1个，如果这一螺栓发生松弛，必然会使柴油机上众多的连接管路的相对位移增大，造成更大的破坏。因此本文即以机脚螺栓的连接强度作为研究重点，暂不考量机脚上的其他4个螺钉连接。

由式 (1)可计算出螺栓连接结合面分离前的组合柔度为1.92×10-6mm/N。结合螺纹连接结构的非线性动力学模型，可得某一螺纹预紧力下的螺栓结构组合柔度曲线(见图3)。可以看出，分离前，柔度保持不变，且曲线经过原点；部分分离时，柔度逐渐增加；完全分离后，也是直线关系，但该直线的延长线不经过原点，与纵轴的交点取决于结构的几何特性和装配预紧力。

图3　等效弹簧变形与螺纹连接受力的非线性关系 Fig.3 Nonlinear relationship between deformation of spring and bolted joint load

在以往的许多设备冲击极限载荷研究中，都将冲击应力响应大于材料静态屈服极限应力σs作为失效标准。但材料在高应变率情况下动态性能会得到提高，因此，采用这一标准对某些材料可能过于保守[9]。另外，机脚螺栓结构失效时常附带一些功能性失效的因素。偏心加载时，随着载荷的加大，螺纹连接结构会发生单边分离，即出现连接面的某一边缘压缩应力变为0情况。此时螺栓所受附加载荷会急剧上升，极大值出现在两者完全分离时刻，分离后螺栓的应力相比分离前会显著增加(见图4)。而螺栓抵抗横向载荷和弯曲载荷的能力差，BV043/85[10]规定的螺纹连接抗冲击设计原则中就有防止螺栓受横向力和扭矩载荷的要求。因此，若提高螺栓连接结构的抗冲击性能，应尽量防止结合面分离。所以本文即规定冲击载荷下，若螺栓结构结合面发生分离，则可能发生螺栓弯曲、甚至剪断等问题，判定结构失效。

图4　附加力F SA与螺纹连接结构受力F A关系 Fig.4 Relationship between additional load F SAand F A

2理论基础

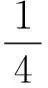
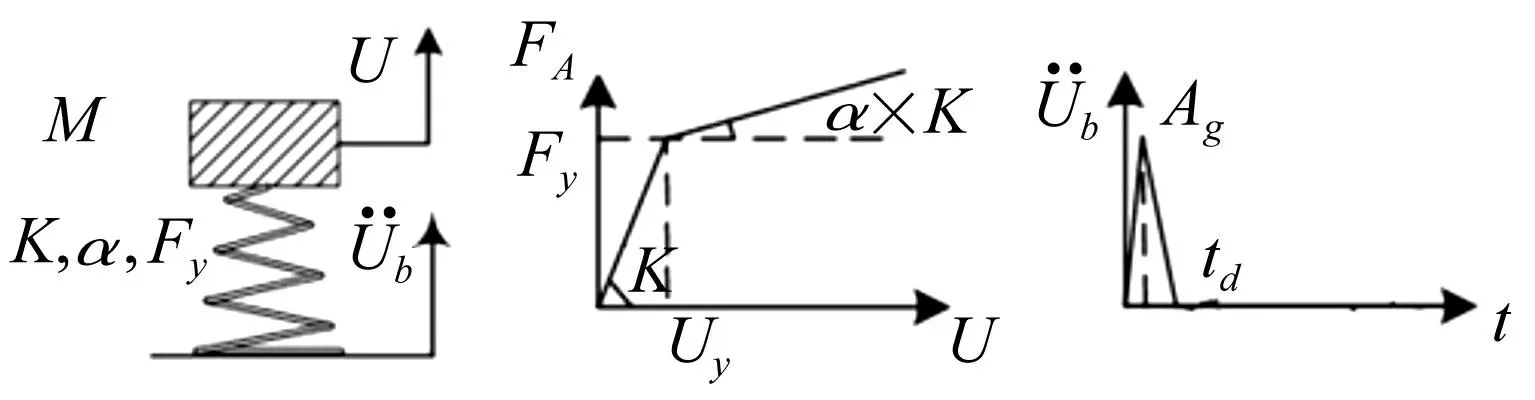
图5　简化动力学模型 Fig.5 Simply dynamic model

2.1载荷的施加及动力学方程

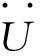
(2)

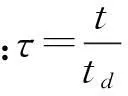
则可得柴油机的冲击动力学方程为：

-2 MA g( b 1 τ+ b 2)- K(1- α) U y

(3)

2.2方程的求解

设受基础冲击的线性系统动力学方程为：

(4)

可得在u(t0)=u0，v0(t0)=v0条件下的通解[12]：

(5)

(6)

令：

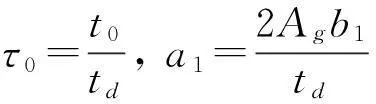
(7)

D(τ)=U(τ)/(Us)

(8)

(9)

Us=MAg/K

(10)

(11)

(12)

式中：f为冲击脉冲的无量纲量，η为拉力Fy的无量纲量。

令：

b3=2πf(b1τ0+b2)+(1-α)ηπf

(13)

b4=2πf

(14)

(15)

(16)

2.3螺栓结构结合面状态分析

参考文献首先假设螺栓结构结合面未分离，则式(15)、式(16)中α=1。[13]中的方法分析，则可将冲击输入分为三阶段：冲击脉冲上升阶段(阶段一)、衰减阶段(阶段二)及自由振动阶段(阶段三)，各阶段参数值见表1。

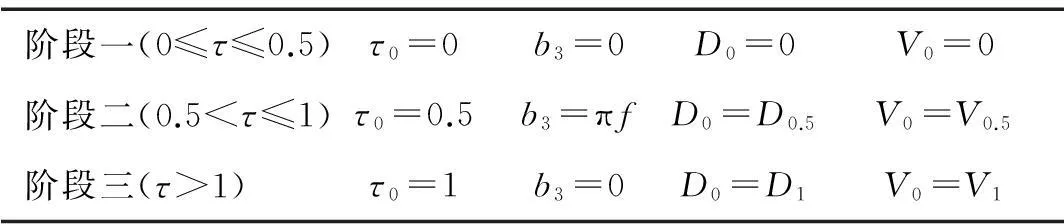
表1　各阶段参数表

则上升阶段：

(17)

衰减阶段：

(18)

(19)

自由振动阶段：

D(τ)=D(1)cos2πf(τ-1)+

V(1)sin2πf(τ-1)

(20)

分别对式(18)及式(20)求导并令等式为0，则可得脉冲衰减阶段及自由振动时段的速度方向改变时刻，此时系统分别达到对应时段的位移峰值响应，对结果化简得：

(21)

(22)

将上述结果分别代入式(18)及式(20)，得出系统最大响应峰值曲线Dm及自由振动阶段的最大响应峰值曲线Df。

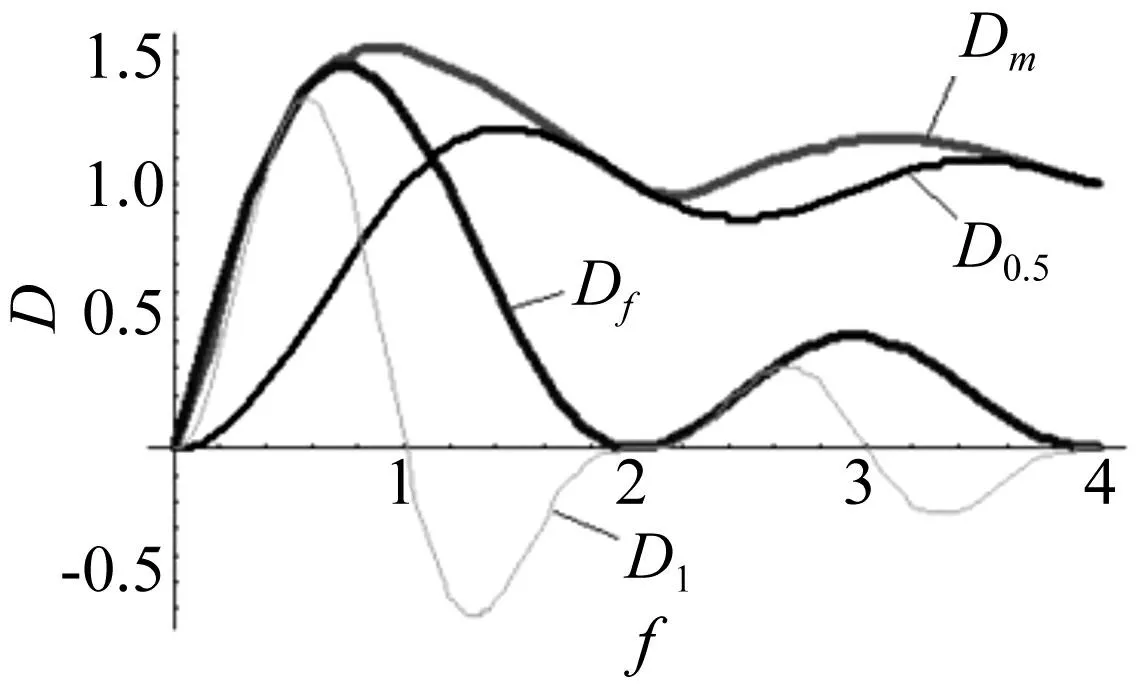
图6　曲线图 Fig.6 Curve graph of f and D

图6显示了自变量为无量纲冲击持续时间f的系统响应的函数曲线。4条曲线分别表示系统最大冲击响应曲线Dm，自由振动最大响应Df，由式(17)计算出的冲击输入峰值时的响应D0.5，由式(18)计算出的冲击输入结束时刻的响应D1。由图5可知，当模型中弹簧变形量达到Uy时，螺栓结合面开始分离，用式(8)将Uy无量纲化得Dy，由图6可知，曲线Dm为其它几条曲线的包络线。显然，当Dy>Dm时，即如果(f,Dy)处于曲线Dm上方，则说明冲击载荷下，螺栓的双弹簧结构的最大变形较小，结合面将不会分离。否则结合面将发生分离。而由式(8)、式(10)、式(12)可知Dy=η。因此只要比较η与Dm的大小即可判别螺栓结构结合面是否分离。当然，柴油机工作时，可能还会承受力矩(如船舶摇晃引起的力矩)，此时机脚螺栓所受载荷可能超出本文所规定的范围。但实际上柴油机的结构复杂，模态丰富，采用单自由度系统代替实际的多自由度系统，会使计算结果偏大，这就在一定程度上抵消了机脚螺栓所受载荷较大情况时的影响。

3机脚螺栓连接冲击响应快速计算实例

用上述理论考核前述机脚螺栓连接抗冲击性能，由前述参数可得K=0.52×109N/m，T=0.004 35 s，现采用文献 [8]所提供的冲击输入，即基础受到加速度激励峰值为1 568 m/s2，脉冲宽度为4.67 ms的三角波垂向冲击输入，连接的抗冲击考核过程如下：

取图3中虚线部分则Qy=26 kN，可得：

对应图6，可判断此时点(f,η)落于曲线Dm曲线之下，因此可判断在此冲击载荷下，螺栓结合面将发生分离，螺栓连接结构失效。这一结果与文献[8]结论一致，图7为通过非线性模型计算所得的螺栓双弹簧模型的冲击响应曲线。在此冲击载荷下等效螺栓连接模型的最大拉伸变形2.18 mm，最大压缩变形1.24 mm。则机脚螺纹连接结构最大拉力158 kN，最大压力644 kN。其最大附加拉力为294 kN，最大附加压力99 kN。根据结构的几何特性和动力学特性以及预紧力，可计算螺纹连接结构的单边分离临界力：如果连接面不发生单边分离，对螺栓的最大附加拉力为80 kN，最大附加压力(释放螺栓的预紧力)为72 kN，可见拉伸时，螺纹连接的受力大于接合面开始分离的临界力，接合面发生了分离。

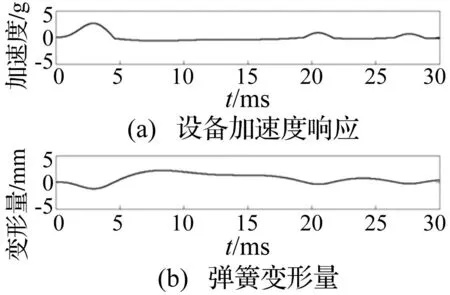
图7　非线性模型的冲击响应 Fig.7 Shock response of nolinear model of rigidly-fixed engine

4实验验证

为检验本文方法，采用某型柴油机冲击响应实验数据进行验证，冲击首先作用于柴油机隔振器下方，通过隔振器与柴油机安装支座传给机脚。在柴油机输出端机脚布置一个ICP式加速度计，测量柴油机机脚的垂向加速度。将所得响应信号经滤波后，分离出机脚螺栓处冲击响应，将其转化为无阻尼的冲击响应加速度谱， 如图 8中实线所示。其中，坐标系为双对数坐标系，冲击响应加速度谱除以 A 进行无量纲化处理， A 为滤波后机脚振动加速度最大值。图 8中虚线为等效三角波转化而得的冲击响应谱。由图8 比较可得，如以三角波作为输入， 多数频率下为过冲。 将此三角波作为冲击输入按上述方法校核机脚螺栓连接强度。结果显示，(f,Dy)处于图6曲线Dm上方，说明在本三角波输入及本次冲击实验下，螺栓结合面没有发生分离。所得结果与实验结果一致。

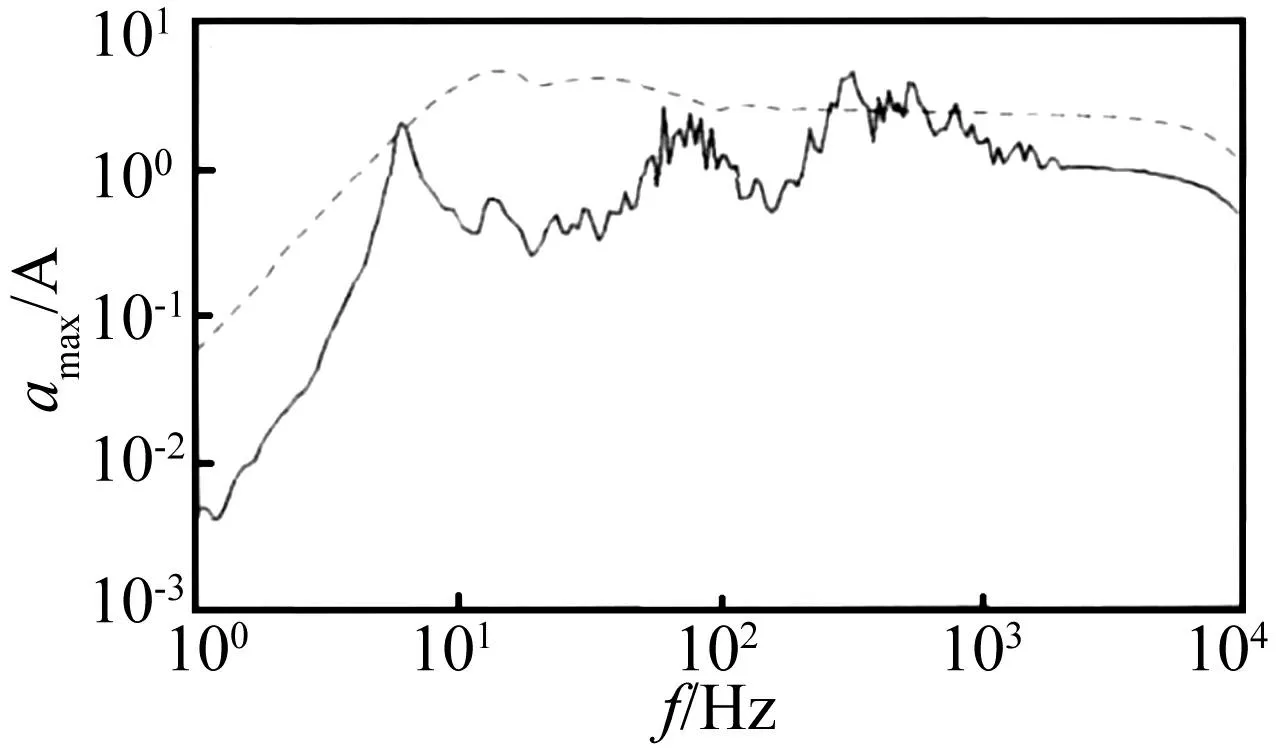
图8　实测信号与等效三角波冲击谱 Fig.8 Shock spectrum of measured signal and equivalent triangular wave

5结论

冲击载荷下，机脚螺栓连接为柴油机等大型船舶设备的薄弱环节之一，由于机脚螺栓与船舶设备尺度上的差异，造成了其抗冲击研究需付出较大的代价，而如果将螺栓连接简化为双弹簧模型，将螺纹连接与其上设备简化为单自由度系统，并利用螺纹连接结合面发生分离时柔度的变化规律，则可以利用本文的理论快速计算其冲击响应结果，校核螺纹连接冲击安全性。由于避免了繁琐的冲击响应及单边分离临界力的计算过程，这种方法省时、简便可行，为螺栓连接的柔度设定，预紧力优化及螺栓连接极限冲击载荷的计算提供了一条便捷途径。当然，将螺栓结构结合面是否发生分离作为螺栓结构失效的判据，可能导致螺栓连接的安全裕度较大。本文提供的方法对冲击载荷下机脚螺栓连接结构强度的判断具有一定的参考价值。

参考文献

[1]姚熊亮，陈建平.水下爆炸二次脉冲压力下舰船抗爆性能研究[J] ．中国造船，2001，42(2):48-57．

YAO Xiong-liang,CHEN Jian-pin. A study on anti-underwater-explosion performance of shipsubjected to gas bubble impulsive pressure[J]. Shipbuilding of China, 2001,42(2):48-57．

[2]冯麟涵. 舰船系统抗冲击性能全局优化方法研究[D]．哈尔滨：哈尔滨工程大学，2009．

[3]计晨，汪玉，杨莉，等.水下爆炸载荷作用下舰用齿轮箱强度极限数值仿真研究[J]. 北京理工大学学报，2011，31(1):8-11．

JI Chen, WANG Yu,YANG Li,et al. Numerical simulation study on intensitythreshold of marin gearbox subjected to underwater explosion load[J]. Transactions of Beijing Institute of Technology, 2011,31(1):8-11．

[4]高浩鹏，黄映云，刘鹏. 引入传递矩阵法的复杂多体系统连接件建模方法研究[J].振动与冲击，2012，31(16):52-55．

GAO Hao-peng,HUANG Ying-yun,LIU Peng. Modeling of linkers in complex multibody system with transfer matrix method[J]. Journal of Vibration and Shock，2012,31(16):52-55．

[5]陈学前，杜强，冯加权. 动载荷下螺栓连接的优化设计[J]. 力学与实践，2005，27(6):32-35.

CHEN Xue-qian, DU Qiang, FENG Jia-quan.The optimal design of bolt joints under dynamic loading[J]. Mechanics and Engineering,2005,27(6):32-35.

[6]Duffey T A. Optimal bolt preload for dynamic loading[J]. International Journal of Mechanical Seciences, 1993,35(3/4):257-265.

[7]VDI2230-2003高强度螺纹连接设计指南[S].VDI committee, 2003.

[8]高洪滨. 柴油机螺纹连接结构冲击动力学特性研究[D]．武汉：海军工程大学，2010.

[9]徐小刚．舰船抗爆抗冲击若干问题研究[D]．哈尔滨：哈尔滨工程大学，2004．

[10]BV0430/85，德国国防军舰建造规范-冲击安全性[S]. 科布伦茨：联邦德国国防装备技术和采购局，1987.

[11]GJB1060.1-91，中华人民共和国国家军用标准-舰船环境条件要求机械环境[S].北京：国防科学技术工业委员会，1991．

[12]Chopra,A.k. Dynamics of Structures[M].Prentice Hall,1995.

[13]George Mylonakis. Yielding oscillator under triangular ground acceleration pulse[J]. Journal of Earthquake Engineering, 2001, 5(2):225-251.