多重分形近似熵与减法 FCM聚类的研究及应用
2016-01-15张淑清,李盼,胡永涛等
第一作者张淑清女,博士,1966年生
邮箱:zhshq-yd@163.com
多重分形近似熵与减法FCM聚类的研究及应用
张淑清,李盼,胡永涛,王佳森,姜万录
(燕山大学电气工程学院河北省测试计量技术及仪器重点实验室, 秦皇岛066004)
摘要:提出了一种基于多重分形与近似熵相结合的信号特征量提取方法,应用于齿轮箱的故障信号诊断中。针对齿轮箱的故障信号的复杂性,先用减法聚类对提取到的信号特征量进行处理,得到初始聚类中心,然后再用模糊C 均值聚类(FCM)作进一步处理,实现齿轮箱故障的自动诊断和识别。多重分形谱提取的特征量如谱宽,可以表示信号的波动程度,而近似熵可以表示信号的复杂程度。两者结合可以得到更加准确的齿轮箱故障信号模式。减法聚类可以有效解决FCM容易陷入局部最优的问题,还可以提高收敛速度。提取的特征参数作为聚类分析的数据,通过计算数据点与聚类中心的隶属度判定所属类型,实现齿轮箱故障类型聚类以及模式识别。通过风力发电机齿轮箱故障诊断实验,证明该方法的可行性和有效性。为齿轮箱故障诊断提供了一种新的有效途径。
关键词:多重分形; 近似熵; 减法模糊聚类; 故障诊断
基金项目:国家自然科学基金(51475405,61077071);河北省自然科学基金(F2015203413)
收稿日期:2014-01-22修改稿收到日期:2014-09-10
中图分类号:TS04文献标志码:A
基金项目:中央高校基本科研业务费专项资金资助项目(QN2011141);高等学校博士学科点专项科研基金资助项目(20120204120017)
Application of multifractal approximate entropy and subtractive FCM clustering in gearbox fault diagnosis
ZHANGShu-qing,LIPan,HUYong-tao,WANGJia-sen,JIANGWan-lu(Institute of Electrical Engineering, the Key Lab of Measurement Technology and Instrumentation of Hebei Province, Yanshan University, Qinhuangdao 066004, China)
Abstract:A feature extraction method based on multifractal approximate entropy was presented and used in gearbox fault diagnosis. Considering the complexity of gearbox fault data, the subtractive clustering was used to obtain an initial cluster center of characteristics. Then the fuzzy C-means clustering(FCM) was used for further processing to achieve automatic gearbox fault diagnosis and identification. The volatility of a signal was expressed by feature values extracted by multifractal spectrum, such as spectral width, and the complexity of the signal was represented by approximate entropy(ApEn). The combination of the two representations can make the patterns of gearbox faults more accurate. The problem of easily falling into local optimum during the FCM clustering process was effectively solved by applying subtractive fuzzy clustering, which also improves the convergence rate. The characteristic parameters extracted were taken as the data used in clustering analysis. In order to achieve gearbox fault clustering and recognition, the membership grades of data points and cluster center were calculated. To prove the feasibility and effectiveness of the method proposed, fault diagnosis experiments on a wind turbine gearbox were implemented. The study provides a new effective way for gearbox fault diagnosis.
Key words:mutifractal; approximate entropy; subtractive fuzzy clustering; fault diagnosis
齿轮箱作为重要的机械部件,承载着加减速、 改变传动方向、分配动力等功能,一旦出现故障,将对整个机器运行造成严重后果,为保证机械设备安全高效运行,齿轮箱故障的诊断与识别是极为重要的[1-2]。齿轮箱故障信号往往呈现出非线性和非平稳特性,传统的振动时域特征值法和频谱分析法等均未考虑振动信号的非线性因素[3];经验模态分解虽能够自适应的处理非平稳非线性信号,但是该方法存在诸如过包络、欠包络、端点效应和缺乏统一的筛分停止准则等问题[4]。这些方法的不足严重影响了齿轮箱故障特征向量提取的效果。
多重分形奇异谱提取间接反映振动信号波动程度的谱宽Δα和能反应振动幅值之比的最大最小概率差Δf,齿轮箱故障信号的多标度、非平稳信号的特点决定了多重分形的故障特征提取方法能够表征齿轮箱故障信号的内在动力学机制[5];近似熵(ApEn)作为信号复杂程度的度量工具可以直接表征振动信号的特征[6]。因此,多重分形谱参数结合近似熵,可以有效揭示隐藏在齿轮箱振动信号内部的动力学行为,准确全面地表达齿轮箱故障信号复杂的故障模式。
模糊C均值(FCM)聚类是用隶属度确定每个数据点属于某个聚类程度的一种聚类算法[7]。该聚类算法以其高效性在工程实际中得到了广泛应用,但该算法对初始聚类中心极其敏感,极易陷入局部最优。引入减法聚类能够有效避免陷入局部最优,并且提高收敛速度。本文将所提取的三个故障向量作为减法模糊聚类的特征参数,可准确达到齿轮箱复杂故障信号诊断和识别的目的。
1多重分形与ApEn的特征提取法
1.1多重分形特征参数提取
多重分形适用于非平稳信号的内在特征信息的精细刻画与准确提取[8]。
将时间序列x(i),i=1,2,…,n,分解为若干个尺寸为ε的小方块,Si(ε)是第i个小方块内所有信号的幅值之和,那么概率测度可以表示为:
(1)
由概率密度Pi(ε)组成的一系列子集,按Pi(ε)的大小划分可以满足如下条件的幂函数子集:
Pi(ε)∝εα
(2)
式中:α为奇异强度。
若具有相同奇异强度的小方块的个数为N(ε),该数与ε在无标度区域内有如下关系:
N(ε)∝ε-f(α)(ε→0)
(3)
式中:f(α)为α的分布密度函数,即多重分形谱函数,通常为光滑的凸函数。
不同的权重因子q表示不同的概率测度Pi在分配函数χq(ε)中的比例为:
χq(ε)≡∑Pi(ε)q
(4)
在无标度区域内存在与χq(ε)的标度关系为:
χq(ε)∝ετ(q)
(5)
(6)
式中:τ(q)为质量指数,-∞
由Legendre变换可以确定多重分形谱如下:
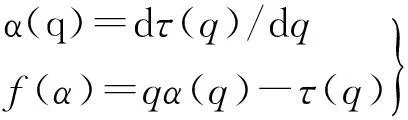
(7)
最后,由多形分形谱提取多重分形参数:
Δα=αmax-αmin
(8)
Δf=f(amin)-f(amax)
(9)
式中:Δα为提取多重分形谱的谱宽。其大小可以反映整个分型结构上概率测度分布的情况,通过该数据的大小可以表示分布的不均匀性,也就是可以间接的表示信号的波动程度。Δf为最大最小概率子集分形维数差,可以反应振动信号振动幅值之比。
1.2近似熵算法提取特征参数
近似熵算法的具体步骤如下[9]:
设采集到的原始数据{x(i),i=1,…,n};
(1)将序列{x(i)}按顺序组成一组m维矢量X(i):
X(i)=[x(i),…,x(i+m-1)]
(10)
式中:i=1~n-m+1,每一个X(i)是由m个数据点构成。
(2)定义Nm(i),i=1~n-m+1。其中Nm(i)为d[X(i)X(j)]小于r的数量,d[X(i)X(j)]表示X(i)和其余X(j)间的距离,r为相似容限,是需要预先给定的值。
(3)定义φm(r)用来描绘序列中的所有m维矢量彼此接近的平均频率,
(11)
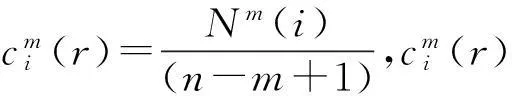
(4)将维数m增加1,重复上面的(1)至(3)步骤可以得到φm+1(r)。
(5)按照理论,此序列的近似熵:
ApEn(m,r,n)=φm(r)-φm+1(r)
(12)
从以上过程可知,近似熵的大小与m,r的大小有关,Pincus指出,通常m=2,r=0.1~0.25SD,SD为原始数据x(i)的标准差。
2减法模糊聚类法与模式识别法
模糊C均值聚类算法(FCM),是模糊聚类中比较常用的算法[10]。但该算法对初始聚类中心十分敏感,极易陷入局部最优。为了解决这个问题,在使用FCM前先采用减法聚类得到初始聚类中心,不但可以获得全局最优解,还能够加快聚类速度。
2.1减法聚类算法
减法聚类从全局出发把全部样本点列为聚类中心的候选点,是一种快速且独立的近似聚类算法[11]。
考虑样本集{xi},i=1,2,…,n;n为样本个数,具体的算法步骤如下:
首先计算样本集中每个点xi的密度指标:
(13)
式中:ra是一个正数,定义了该点的邻域半径,一般取ra=0.5。把密度指标最大的数据点xc1选为第一个聚类中心,对应的密度指标为Dc1。
然后假定xci为第i次选出的聚类中心,对应的密度指标为Dci,其余每个点xi的密度指标为:
(14)
式中:rb也为一个正数,定义了一个密度指标显著减小的邻域,一般rb=(1.2~1.5)ra。
重复以上过程,直至:
(15)
式中:0<δ<1,决定最终产生的初始化聚类中心数目,一般δ=0.5时可获得最多的聚类数目Cmax。
从上述步骤可以看出,减法聚类中心出现的顺序是由密度指标决定的,密度指标越大则出现的越早,也越有可能是合理的初始聚类中心。因此在以聚类数为c的检测中,只需以减法聚类产生的前c个聚类中心作为新的初始中心就可以了,而不需要再重新进行初始化,从而提高聚类的效率[12]。
2.2模糊C均值聚类算法
给定一个样本集{xi},i=1,2…,n,n为样本个数,FCM将该样本分为c个模糊组,并且计算出每个族的聚类中心,使非相似性指标函数达到最小值。每个点是通过隶属度来确定与各组之间的关系,每个隶属度的大小在[0,1]的范围之内,再经过归一化规定,一个数据属于各组的隶属度之和为1[13]。
(16)
式中:∀i=1,2,…,n。
FCM的价值函数可以表示为:
(17)
式中:U为模糊隶属矩阵;uij为标准化后数据集的隶属度,总和为1,且uij∈(0,1);cj是某一类的聚类中心,dij表示的是第i个数据点与第j类聚类中心的欧氏距离,m是一个不小于1的加权指数。
为了使J(U,c1,c2,…,cn)函数达到最小值,必须满足如下的条件:
(18)
(19)
由以上两个必要条件可知,模糊C聚类是一个简单的运算过程。依据式(17)计算目标函数,如果它相对于上次目标函数值的该变量小于某个确定的阈值ε,则算法停止。
2.3减法模糊聚类算法
(1)初始化聚类参数:邻域半径ra、rb,比例参数δ,FCM聚类数c,加权指数m和阈值ε等。
(2)利用减法聚类得到Cmax(Cmax>c)个聚类中心,从中选前c个作为FCM的初始聚类中心。
(3)再进行FCM聚类,得到聚类结果。
2.4贴近度择近原则
模糊模式识别大致有两种方法:最大隶属度法和贴近度择近法。前者适用于个体样本的模式识别,后者适用于群体样本的模式识别。本文选择贴近度择近原则进行故障模式识别[14]。
设A和B是论域W上的两个模糊子集,定义A和B之间的贴近度为N(A,B)。常用的计算公式有欧式贴近度、海明贴近度和最大最小贴近度,这里采用最为常用的最大最小贴近度法。
设论域W={w1,w2,…,wn},则最大最小贴近度为:
(20)
式中:∨和∧分别为取最大值和最小值,uA(w)和uB(w)分别为论域W中元素A、B的隶属度。
给定论域W上的模糊子集A1,A2,…,An及另一模糊子集B,若:
N(A,B)=maxN(A1,B),…,N(An,B)
(21)
则认为B与Ai最贴近,B应归为模式Ai,这就是贴近度择近原则。
本文模糊聚类识别算法就是通过计算数据点与聚类中心的隶属贴近度判定所属类型,以实现聚类和模式识别,从而达到对不同故障信号的特征参数的类别的区分。
3故障诊断实验

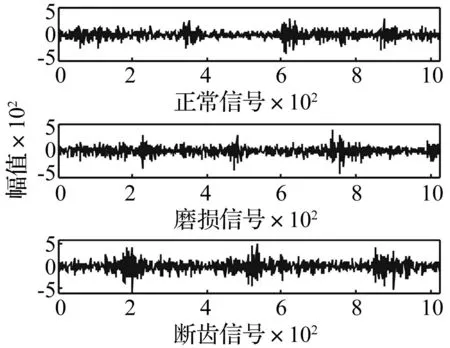
图1 齿轮箱3种信号局部图 Fig.1 Three local signal of gear box
采用多重分形谱对三种状态进行分析,取q为[-50,50]中所有整数。图2为质量指数τ(q)与q的关系图。从图2可知,约在横坐标为0的处有一个明显的拐点,体现出明显的非线性,可以说明这三种信号具有多重分形性。
图3为三种信号的多重分形谱,根据对多重分形谱的分析可以求得在多重分形分析中的两个常见的参数,谱宽Δα和最大最小概率差Δf。
根据上文中所介绍的近似熵算法的具体步骤对三种状态信号进行近似熵计算,并将其与谱宽Δα和最大最小概率差Δf构成聚类分析的特征向量。


图2 三种信号的τ(q)-q图Fig.2Relationbetweenτ(q)andqofthethreekindsofsignal图3 三种状态信号的多重分形奇异谱Fig.3Themulti-fractalsingularityspectrumofthethreekindsofsignal
由于本文所提取的是三个特征参数,所以需构造一个三维的故障特征向量A:
A=[ai1,aj1,af1]
(22)
式中:ai,aj,af分别表示的是同一个信号的谱宽,最大最小差值,以及近似熵的值。由于不同类别之间的差别不是特别的突出,因此将该矩阵进行标准化处理:
(23)
式中:分母表示的是各列相同类型特征量中的最大与最小的差值,分母就是某个特征值相对于最小值的大小。通过标准化计算,可以把特征值的范围限制在[0,1]区间之内。通过之前对实验平台的介绍可以知道故障类型是3类,所以在模糊聚类数c=3,邻域半径ra=0.5,rb=0.6,比例参数δ=0.5,加权指数m=2和阈值ε=0.000 1。按照减法模糊聚类的运算不断迭代计算,直到满足收敛条件为止,聚类的结果见图4。从图4可知,聚类曲线呈现出不规则性,因而能够完成对不同状态、大小和密度的数据进行聚类。说明了对于由多重分形与近似熵相结合提取的特征量,用减法模糊聚类可以达到明显的聚类效果,可以作为故障模式识别的有效途径。
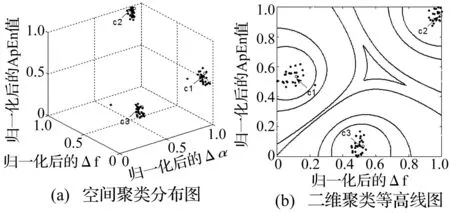
图4 三种状态信号的模糊C聚类图 Fig.4 FCM clustering of the three kinds of signal
在以上聚类分析基础上,我们对各类故障进一步识别,通过计算待测样本标准化特征向量与故障聚类中心的最大最小贴近度,同时根据“贴近度择近原则”达到识别故障类型的目的。各种故障的聚类中心见表1。

表1 各种故障的聚类中心
已知三种状态的聚类中心,现对一种故障类型进行识别,待测样本X=[0.657 8,1.530 7,1.544 7],计算待测样本特征向量与正常、磨损、断齿故障三种状态聚类中心的最大最小贴近度,结果如下:
Nc1=0.572 0,Nc2=0.552 4,Nc3=0.963 3
Nc1,Nc2,Nc3分别为待测样本标准化特征向量与故障聚类中心c1,c2,c3的最大最小贴近度。通过以上的数据可以看出,待测数据与断齿聚类中心的贴近度最大,根据贴近度择近原则可以判断该故障信号是一个断齿信号,理论的判断结果与实际相符合。
为了进一步验证该故障诊断方法的有效性,随即采集正常、磨损、断齿故障三种状态特征向量各2组,计算各组聚类中心的贴近度,理论的结果应该为:1~2组中Nc1大于Nc2和Nc3,3~4组中Nc2大于Nc1和Nc3,5~6组中Nc3大于Nc1和Nc2。依据贴近度的大小给待测样本做出判定,实际计算值和诊断结果见表2。

表2 故障诊断结果
表2中6组待测数据的测试结果与实际情况相符合,验证了该方法对齿轮箱故障的有效性。
4结论
提出多重分形近似熵与减法模糊聚类的齿轮箱故障诊断方法。用多重分形提取到能够间接表示振动信号特征量的参数:谱宽Δα和最大最小概率差Δf。然后提取该振动信号的近似熵。将这三个参数作为减法模糊聚类的特征向量,通过计算数据点与聚类中心的隶属度判定故障所属类型,从而达到齿轮箱故障类型聚类以及模式识别的目的。对某风力发电实验平台的齿轮箱实测信号进行了诊断和识别,表明该方法能够解决故障模式相近的复杂齿轮箱振动信号的分类问题,为齿轮箱故障诊断提供了一种新的有效途径。
参考文献
[1]林近山, 陈前.基于非平稳时间序列双标度指数特征的齿轮箱故障诊断[J].机械工程学报, 2012, 48(13): 108-114.
LIN Jin-shan, CHEN Qian. Fault diagnosis of gearboxes based on the double-scaling-exponent characteristic of non-stationary time series [J]. Journal of Mechanical Engineering, 2012, 48(13): 108-114.
[2]唐新安, 谢志明, 王哲,等. 风力机齿轮箱故障诊断[J].噪声与振动控制, 2007(1): 120-124.
TANG Xin-an, XIE Zhi-ming, WANG Zhe, et al.Fault diagnosis of gearbox for wind turbine [J]. Noise and Vibration Control, 2007(1): 120-124.
[3]祝志慧, 孙云莲, 李洪. 基于EMD的时频分析方法的电力故障信号检测[J].武汉大学学报:工学版, 2007, 40(05): 112-119.
ZHU Zhi-hui, SUN Yun-lian, LI Hong. Power fault detection using empirical mode decomposition [J].Engineering Journal of Wuhan University, 2007, 40(05): 112-119.
[4]Frei M G,Osorio I.Intrinsic time-scale decomposition: time-frequency-energy analysis and real-time filtering of non-stationary signals [J].Proceedings of the Royal Society A, 2007, 463(2078): 321-342.
[5]林近山,陈前.基于多重分形去趋势波动分析的齿轮箱故障特征提取方法[J].振动与冲击, 2013, 32(2): 97-101.
LIN Jin-shan, CHEN Qian. Fault feature extraction of gearboxes based on multi-fractal detrended fluctuation analysis[J]. Journal of Vibration and Shock, 2013, 32(2): 97-101.
[6]胥永刚, 李凌均, 何正嘉. 近似熵及其在机械设备故障诊断中的应用[J].信息与控制, 2002, 31(06): 543-551.
XU Yong-gang,LI Ling-jun, HE Zheng-jia. Approximate entropy and its applications in mechanical fault diagnosis[J]. Information and Control, 2002, 31(06): 543-551.
[7]Bezdek J C.Pattern recognition with fuzzy objective function slgorithms[M].New York:Plenum Press,1981.
[8]王祖林,周荫清. 多重分形谱及其计算[J]. 北京航空航天大学学报, 2000,26(3): 256-258.
Wan Zu-lin, Zhou Yin-qing. Multifractal spectrum and calculation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2000, 26(3): 256-258.
[9]戴桂平.基于EMD近似熵和DAGSVM的机械故障诊断[J].计量学报, 2010, 31(5): 467-471.
DAI Gui-ping. Mechanical fault intelligent diagnosis based on EMD-Approximate entropy and DAGSVM[J]. Acta Metrologica Sinica, 2010, 31(5): 467-471.
[10]Abásolo D, Hornero R, Espino P, et al.Analysis of regularity in the EEG background activity of Alzheimer’s disease patients with Approximate Entropy[J].Clinical Neurophysiology, 2005, (116): 1826-1834.
[11]肖春景, 张敏. 基于减法聚类与模糊c-均值的模糊聚类的研究[J]. 计算机工程, 2005,31(7): 135-137.
XIAO Chun-jing, ZHANG Min. Research on fuzzy clustering based on subtractive clustering and fuzzy c-means[J]. Computer Engineering, 2005, 31(7): 135-137.
[12]蔡威, 程俊杰. 基于减法聚类的GK模糊聚类研究[J]. 兰州交通大学学报, 2011, 30(6): 50-54.
CAI Wei, CHENG Jun-jie. Research on GK fuzzy clustering algorithm based on subtractive clustering[J]. Journal of Lanzhou Jiaotong University, 2011, 30(6): 50-54.
[13]徐超, 张培林, 任国全,等. 基于改进半监督模糊C均值聚类的发动机磨损故障诊断[J].机械工程学报, 2011, 47(17):55-60.
XU Chao, ZHANG Pei-lin, REN Guo-quan, et al. Engine wear fault diagnosis based on improved semi-supervised fuzzy c-means clustering[J]. Journal of Mechanical Engineering, 2011, 47(17): 55-60.
[14]张淑清, 张金敏, 赵玉春. 基于混沌和模糊聚类的机械故障自动识别[J].机械工程学报, 2011, 47(19):81-85.
ZHANG Shu-qing, ZHANG Jin-min, ZHAO Yu-chun. Automatic diagnosis techniques of machinery fault based on chaos and fuzzy clustering analysis[J]. Journal of Mechanical Engineering, 2011, 47(19): 81-85.

