基于二阶摄动理论的不确定系统小干扰稳定分析方法

马 静，彭明法，王 彤，杨奇逊

（华北电力大学 新能源电力系统国家重点实验室，北京 102206）

0 引言

随着电网规模的不断扩大及运行方式的灵活多变，电力系统的低频振荡问题愈加突出[1-4]。目前，低频振荡分析方法主要分为轨迹分析法模型分析法。后者又可分为确定性模型法和不确定性模型法。长期以来，电力部门在规划和运行中都采用确定性模型法分析系统稳定性，而忽略了网络拓扑、模型、参数和运行工况等不确定因素的影响，为此，不确定性模型法通过建立不确定因素与状态变量，以及状态变量与特征根之间的关系，利用不确定性特征根反映不确定因素对系统稳定性的影响，更符合实际情况。不确定性模型法主要包括概率模型[5-6]和区间模型[7-8]2种。与概率模型相比，区间模型所需的统计学参数较少且易于获取，目前，对该方法的研究主要集中在分析单一运行参数的不确定性变化、区间限值处对应的系统运行状态、运行参数微小波动情况下评估系统的小干扰稳定性等方面[9-10]。对如何解决多运行参数波动较大情况下，连续描述区间内及限值处对应的系统运行状态等问题亟待进一步研究。

围绕这些问题，本文提出了一种考虑多运行参数不确定性的低频振荡分析方法。首先，建立不确定信息下获取系统振荡模式分布情况的复模态二阶摄动模型，在此基础上，连续描述运行状态在不确定变化区间内振荡模式阻尼比的变化轨迹。IEEE 16机68节点系统仿真结果验证了该方法的正确性和有效性。

1 基于二阶摄动理论的小干扰稳定分析原理

考虑区间不确定性的系统特征解问题可描述为：

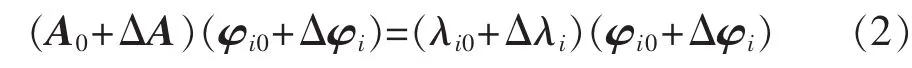
由矩阵摄动理论[12-14]，式（2）的特征解可表示为：

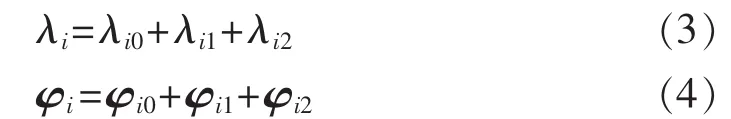
其中，λi、φi分别为系统的特征值、右特征向量；λi0、φi0分别为系统确定性部分的特征值、右特征向量；λi1、λi2分别为特征值的一阶和二阶摄动值；φi1、φi2分别为右特征向量的一阶和二阶摄动值。

将式（3）、式（4）代入式（2），且忽略三阶及三阶以上无穷小量，可得：

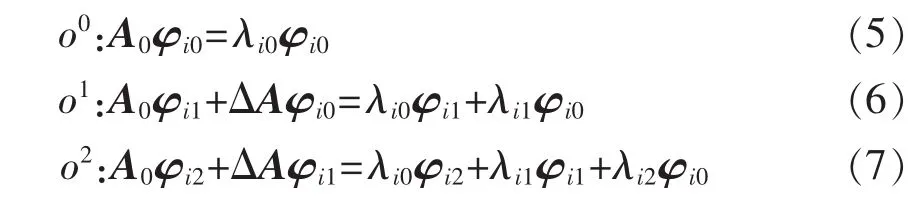
左特征向量ψi与右特征向量φj经过规范化后满足下列关系式：

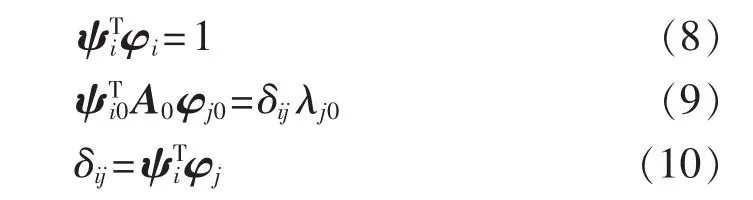
当 i=j时，δij=1，当 i≠j时，δij=0。

根据二项式原理，特征向量一阶摄动值φi1和二阶摄动值φi2可以通过确定性部分的右特征向量φi0表示：

其中，n为状态矩阵的阶数。

将式（11）代入式（6），式（12）代入式（7），且式（6）与式（7）两边同时左乘ψTi0，再根据左右特征向量的正交性可得：

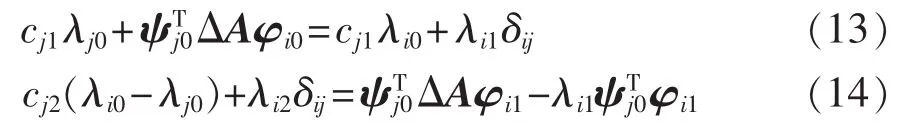
当i=j时，可得特征值的一阶摄动值和二阶摄动值：

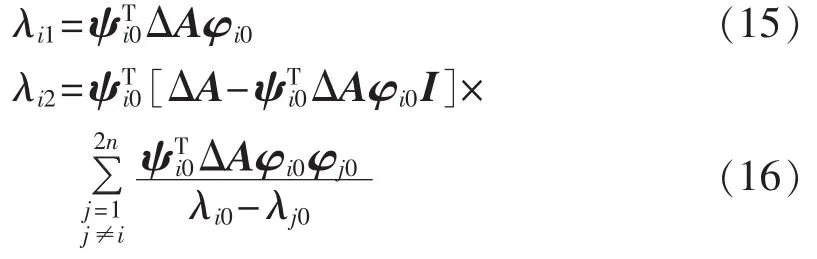
将式（15）和式（16）代入式（3），可计算出系统参数变化后的特征值二阶近似值：

2 应用算例

以IEEE 16机68节点[15]的新英格兰—纽约互联系统为例，如图1所示，该系统可分为五大区域。发电机采用六阶详细模型，励磁采用IEEE-DC1型励磁，负荷模型采用WECC负荷模型，有功负荷中包含80%的恒有功负荷，20%的电动机负荷，无功负荷中包含80%的恒无功阻抗负荷，20%的电动机负荷。矩阵A的具体形成详见软件Power System Toolbox，系统在区间中值处的低频振荡主导模式见表1。利用MATLAB 7.6.0进行摄动分析。

考虑系统运行方式和结构参数的区间不确定性，其中系统运行方式的不确定性以16机机端电压UG16和有功功率PG16，以及37节点负荷的有功功率PL为例进行分析；而系统结构参数的不确定性则采用15机的惯性时间常数M15和暂态电抗x′d15进行考察。不确定性区间分布均为其中值的±20%。计算结果表明，平均每次摄动所需的时间为0.03s，而利用QR计算方法的时间为0.04s，并且随着矩阵维数的上升，利用摄动方法计算特征值的效率越高。

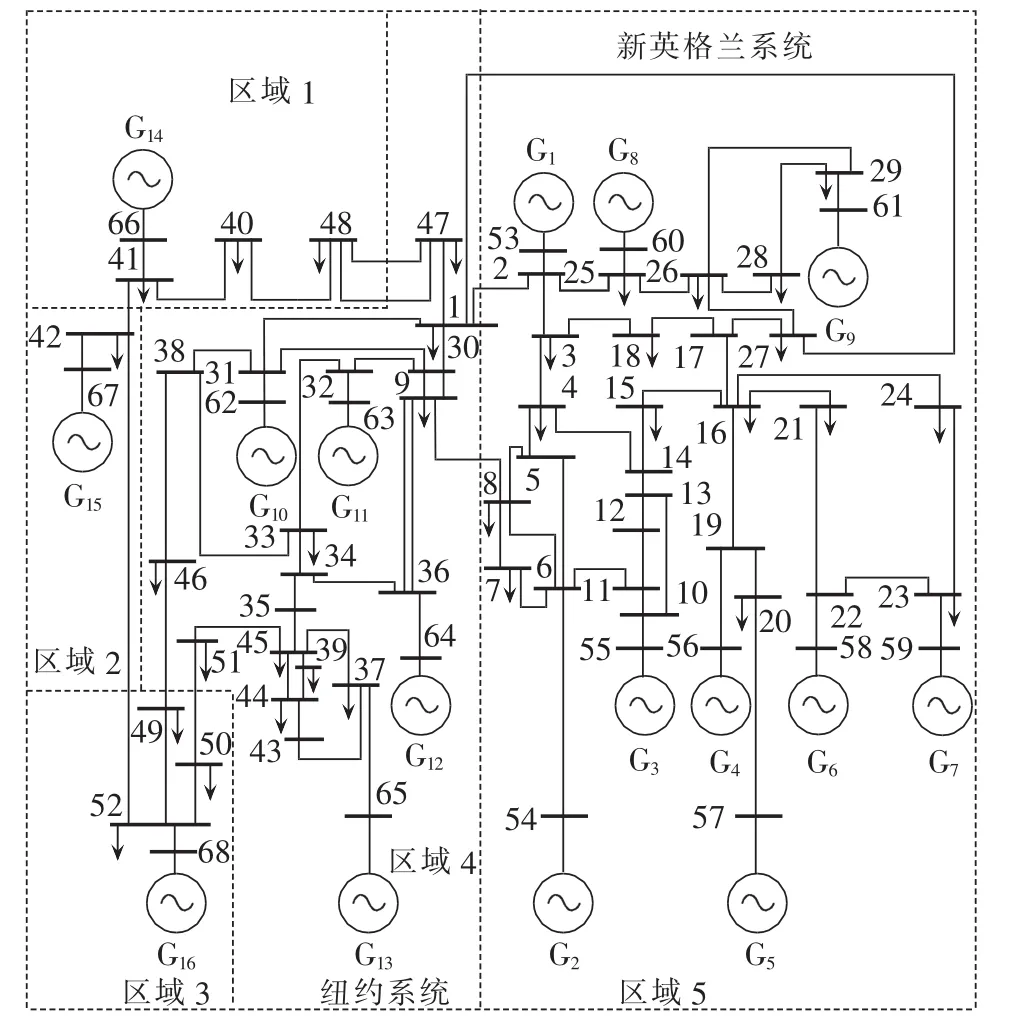
图1 IEEE 16机68节点系统接线图Fig.1 Connection diagram of IEEE 16-generator 68-bus system

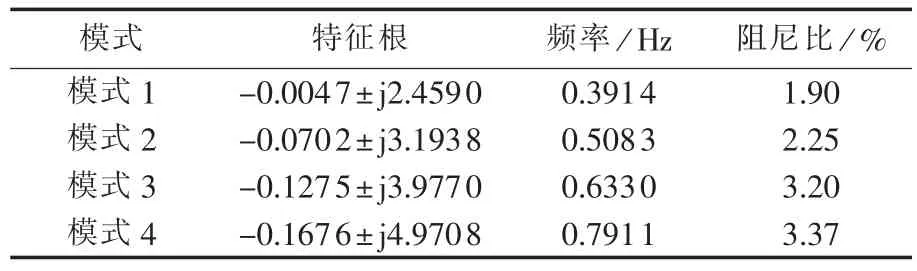
表1 低频振荡主导模式Tab.1 Dominant mode of low-frequency oscillation

2.1 考虑系统运行方式不确定性的阻尼比区间分布

系统运行方式在区间范围内变化时，相应的区间振荡模式阻尼比区间如表2所示，表中UG16、PG16、PL取值范围分别为 0.8～1.2 p.u.、32～46MW、48～72MW。由表2可知，不确定参数UG16和PG16对模式1阻尼比的影响程度最大；对模式2阻尼比的影响程度次之；对模式3和模式4阻尼比的影响较小。PL对模式3阻尼比的影响程度最大，而对模式1、模式2以及模式4的阻尼比几乎没有影响。

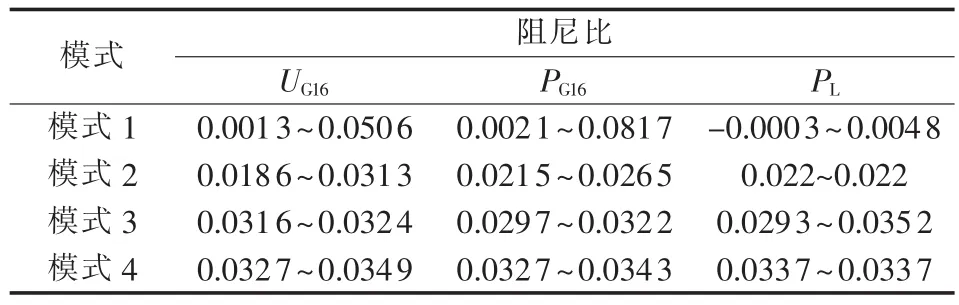
表2 系统运行方式不确定时阻尼比区间分布Tab.2 Interval of damping ratio under uncertainty of operation mode

考虑到模式1参与振荡的机组最多，是典型的区间振荡模式，因此本文以模式1为例，分析不同运行方式在不确定区间内变化时，其阻尼比的变化趋势，如图2—4所示，图2中UG16为标幺值，后同。

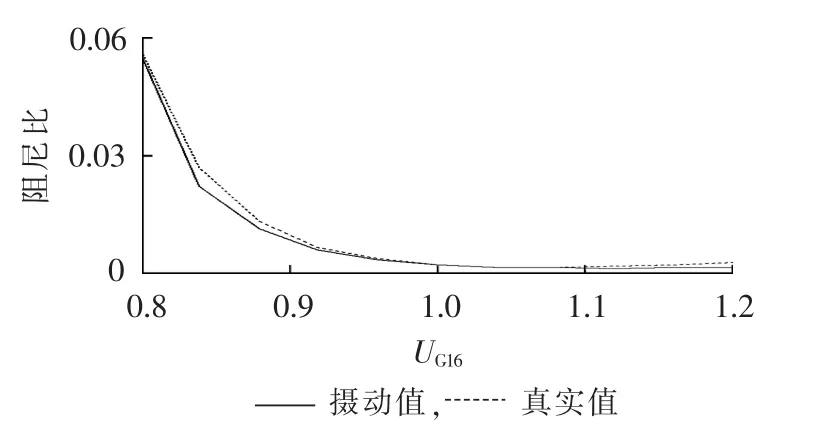
图2 模式1阻尼比随UG16变化曲线Fig.2 Damping ratio of mode 1 vs.UG16

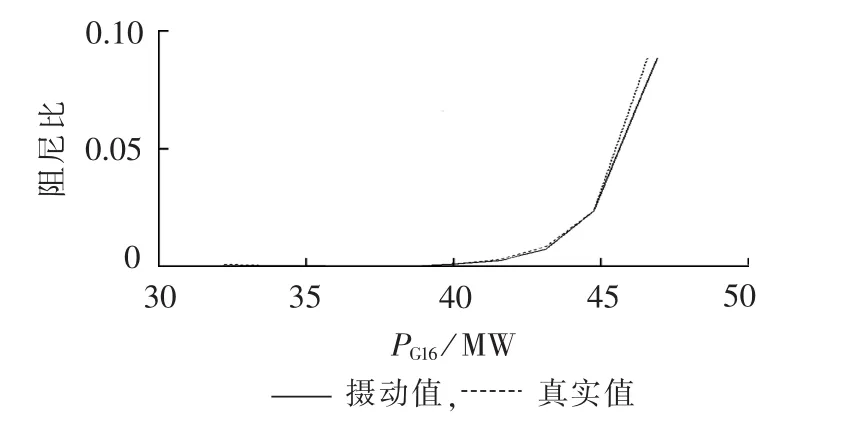
图3 模式1阻尼比随PG16变化曲线Fig.3 Damping ratio of mode 1 vs.PG16

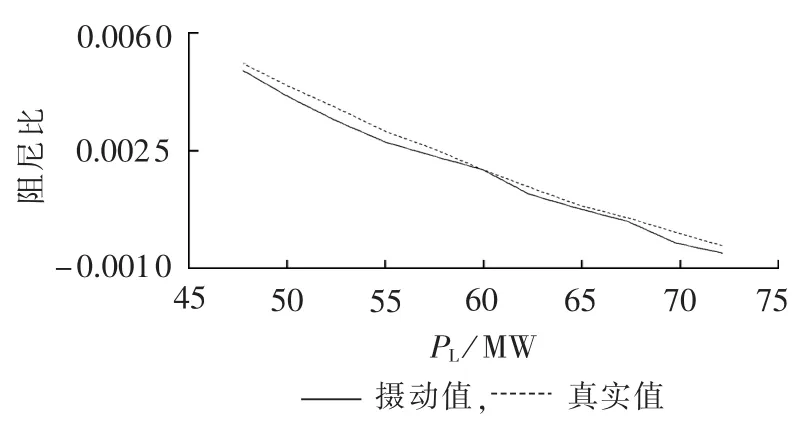
图4 模式1阻尼比随PL变化曲线Fig.4 Damping ratio of mode 1 vs.PL

由图2—4可知，16机机端电压升高时，模式1阻尼比急剧减小，当减至最小值后又缓慢增加；16机有功增大时，模式1的阻尼比缓慢减小，在减至最小值后又迅速增加；37节点负荷有功增加时，模式1的阻尼比单调递减，逐渐由正阻尼模式变为负阻尼模式。

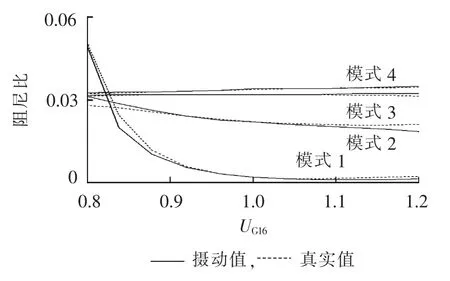
图5 区间模式阻尼比随UG16变化轨迹Fig.5 Damping ratio of inter-area mode vs.UG16

由上面分析可知，不同运行参数在区间范围内变化时，对振荡模式的阻尼比影响程度不同。为了更全面地描述不同模式阻尼比与系统运行状态的对应关系，以UG16在不确定区间内变化为例，分析各模式的阻尼比随其变化规律。如图5所示，模式1的阻尼比随UG16的增大而迅速减小，当减小至最小值后，又随UG16的增大而逐渐增加；模式2的阻尼比与模式1变化规律相同；模式3的阻尼比随UG16的增大而逐渐增加，但达到最大值后，又随UG16的增加而逐渐减小；模式4的阻尼比则随着UG16的增大呈单调递增的趋势。同理，也可分析当PG16、PL在不确定区间内变化时，各模式的阻尼比随其变化的曲线，本文不再赘述。

由图2—5还可以看出，在运行方式变化区间比较大的情况下，利用二阶摄动理论得到的阻尼比变化曲线与真实阻尼比变化曲线极为接近，由此验证了本方法的准确性和有效性。

2.2 考虑系统结构参数不确定性的阻尼比区间分布

系统结构参数在区间范围内变化时，相应的区间振荡模式阻尼比区间如表3所示，表中M15、x′d15取值范围分别为 240～360 s、0.00228～0.00342 p.u.。由表3可知，不确定参数M15对模式4的阻尼比影响程度最大，对模式1的阻尼比影响程度次之，对模式2和模式3的阻尼比几乎无影响。同时，不确定参数x′d15对各模式的阻尼比几乎无影响。

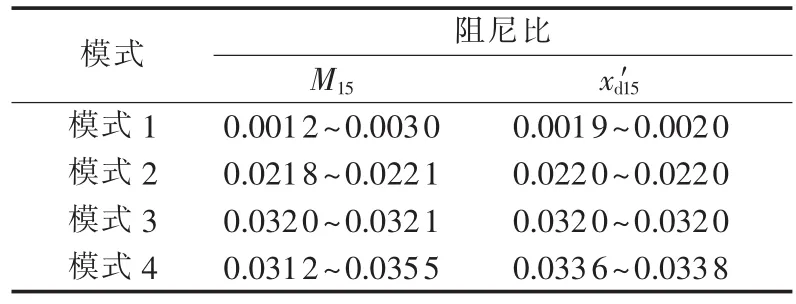
表3 系统结构参数不确定时区间阻尼比区间Tab.3 Interval of damping ratio of inter-area mode under uncertainty of system structural parameters

考虑到结构参数M15和x′d15变化时，对模式4阻尼比的影响程度最大，因此本文以模式4为例，分析结构参数在不确定区间内变化时，其阻尼比的变化趋势，如图6、7所示，图7中x′d15为标幺值。由这2幅图可知，当M15增大时，模式4的阻尼比单调增加；但x′d15增大时，模式4的阻尼比虽然有增加的趋势，但其增加程度甚小，几乎可以忽略不计。

由以上分析可知，不同结构参数在区间范围内变化时，对振荡模式的阻尼比影响程度各异。为了更全面地揭示不同模式阻尼比与系统结构参数间的关系，以M15在不确定区间内变化为例，分析各模式的阻尼比随其变化规律。如图8所示，模式1的阻尼比随M15的增加而逐渐减小，模式2、3的阻尼比随M15的增大几乎不变化，而模式4的阻尼比则随M15的增大而增大。同理，还可分析当x′d15在不确定区间内变化时，各模式的阻尼比随其变化的曲线，在此不再详述。

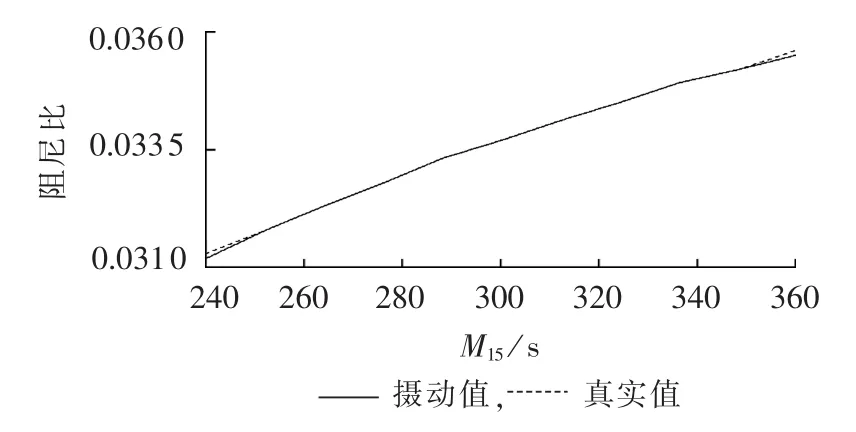
图6 模式4阻尼比随M15变化曲线Fig.6 Damping ratio of mode 4 vs.M15

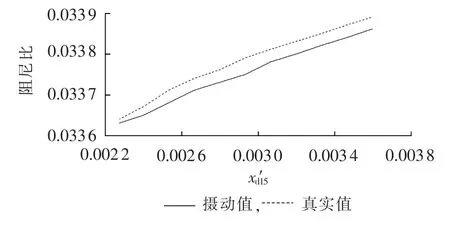
图7 模式4阻尼比随x′d15变化曲线Fig.7 Damping ratio of mode 4 vs.x′d15

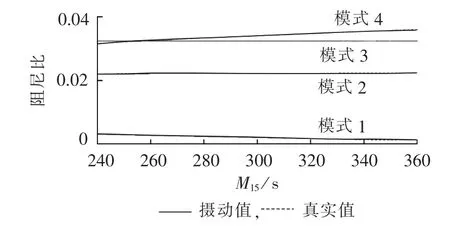
图8 区间模式阻尼比随M15变化轨迹Fig.8 Damping ratio of inter-area mode vs.M15

由图6—8还可以看出，在结构参数变化明显的情况下，利用二阶摄动理论得到的阻尼比变化曲线准确度极高，符合真实情况，由此进一步验证了本方法的有效性和可行性。

3 结论

本文提出一种基于二阶摄动理论和区间模型分析低频振荡模式及其阻尼比的方法。首先，建立了不确定信息下获取系统振荡模式分布情况的复模态二阶摄动模型。然后，连续描述运行状态在不确定变化区间内，振荡模式阻尼比的变化轨迹。IEEE 16机68节点系统的仿真结果表明：一方面不同运行参数在区间范围内变化时，对振荡模式的阻尼比影响程度不同；另一方面，同一运行参数在区间范围内变化时，对不同振荡模式的阻尼比影响各异。同时，当系统中不确定参数发生较大变化时，该方法仍能较准确地评估系统的小干扰稳定情况，并可为运行人员提供更加全面的信息，以改善关键振荡模式的阻尼。