分段线性系统的振动性能分析

第一作者吴志强男，博士,教授，1968年生

邮箱：zhiqwu@tju.edu.cn

分段线性系统的振动性能分析

吴志强， 雷娜

(天津大学机械工程学院力学系，天津300072)

摘要：分析了一类含非连续阻尼的单自由度分段线性系统的振动性能，以研究某些参数对系统振动性能的影响。首先建立分段线性系统的数学模型，利用平均法求解，获得系统的幅频特性和相频特性；然后利用约束分岔理论，计算转迁集，得到系统可能的幅频响应类型，并利用幅频响应方程进行稳定性分析；最后计算系统的传递率，讨论了阻尼和刚度系数对传递率的影响，同时发现传递率曲线也产生了多解现象。

关键词：幅频响应；奇异性；稳定性；跳跃；减振

基金项目：国家自然科学基金(11172198)

收稿日期：2013-09-12修改稿收到日期：2013-12-12

中图分类号:TB535.1文献标志码：A

Vibration performance analysis of piecewise linear system

WUZhi-qiang,LEINa(Department of Mechanics, School of Mechanical Engineering, Tianjin University, Tianjin 300072, China)

Abstract:The vibration performance of a single degree of freedom system with piecewise linear terms and discontinuous damper was investigated, aiming to clarify the influence of some system parameters on the system’s behaviors. A mathematic model of the piecewise linear system was built. By employing an averaging method, the magnitude-frequency characteristic and phase-frequency characteristic functions of the system under primary resonance excitation were obtained. The transition boundary was calculated in accordance with the functions on the basis of the constraint bifurcation theory as well as all the types of the amplitude-frequency responses. The functions were also used for stability analysis. The critical parameter boundary to avoid jumping phenmenon was calculated by qualitatively analyzing the amplitude-frequency responses in the sub-regions of the transition sets. The feasibility of the theoretical study was verified by numerical calculations. In addition, the influences of damping and stiffness coefficients on the global force transmissibility were discussed, and it is found that on the transmissibility curve, the multi-solution problem also appears.

Key words:amplitude-frequency response; strangeness; stability; jump; vibration reduction

间隙的作用和影响在动力机械中普遍存在，除必须的设计要求含有间隙外，装置的安装、加工误差或后期使用中产生的磨损都会最终导致间隙的出现。由于间隙的存在，接触状态会发生变化，导致构件之间出现接触、脱离、再接触、再脱离地重复冲击，对动荷载和系统的动态特性产生不良影响，甚至产生安全隐患。例如，轮对与钢轨之间的碰撞，加剧了高速列车的不平稳运动，影响了列车运行的稳定性与舒适度；又如重载列车转向架的悬挂系统、柴油机轴系装配的分段线性缓冲器、振动筛和振动输送机的分组弹簧等都很好的利用了间隙的特点，极大的改善了系统的振动特性。因此对于含有间隙的非线性碰撞振动系统的动力学研究就显得尤为重要了。

近年来，国内外学者研究了含间隙振动系统的稳定性与分岔[1]、奇异性[2]、概周期碰撞运动[3]、余维二分岔及混沌控制[4- 5]以及减振[6-7]等问题。

本文针对含间隙的弹性碰撞振动系统为研究对象，将此弹性碰撞振动系统简化为一对称的分段线性模型(见图1)，运用平均法求得幅频特性与相频特性，然后基于约束分岔理论[8]，计算转迁集，得到系统可能的幅频响应类型；并对系统进行了稳定性和减振分析，讨论了阻尼和刚度系数对系统振动性能的影响。

1分段线性系统运动分析

1.1系统动力学模型

图1为对称分段线性弹簧系统，当振幅小于间隙时，只有主弹簧起作用，系统作线性振动；当振幅大于间隙时，质量块与副弹簧反复接触后又分离，因而系统的振动是非线性的。系统振动微分方程为

(1)

(2)

式中：K1、K2为弹簧刚度，C1、C2为弹簧阻尼，、P分别为激振角频率和幅值，D为间隙值。

为得到振动方程的无量纲形式，引入如下变换及组合参数

代入式(1)和式(2)可得

(3)

(4)

由于无量纲过程中特征长度选为10倍的间隙，使得无量纲间隙为0.1，这为系统主共振周期响应的近似分析奠定了基础。

1.2系统动力学模型

为考虑主共振(ω=1)情况，将系统的振动方程改写为

(5)

假设系统存在一次近似解形式如

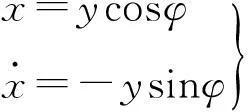
(6)

式中：φ=ωt+θ，应用平均法[9]可将式(5)化成振幅、相位为未知量的标准方程，又因振幅和相位的导数都是O(ε)量级的周期函数，所以代之以一个周期的平均值得

(7)

式中：B(y)和B(y)为分段函数

B(y)=

(8)

B*(y)=

(9)

对于非线性系统，通常关心的是系统受迫振动的稳态值，于是令

消除变量φ，求得系统的稳态幅频响应方程为

[-ζ1y+B(y)]2+

(10)

解出ω可得

(11)

当系统参数均给定时，由式(10)或式(11)可得幅频响应曲线。不同的参数值，可对应不同类型曲线，也可能对应相同类型曲线，要讨论参数对曲线类型的影响，奇异性方法是很好的工具。由于方程是分段的，因此要用约束分岔理论分析方法。

2幅频响应分类

为分析参数变化时，幅频响应曲线类型的变化，选择振幅y为状态变量，激励频率ω为分岔参数，主弹簧阻尼比ζ1和激励幅值p为开折参数，取ζ2=0.5，k=0.5，根据约束分岔理论可求得非空转迁集[8]将开折参数ζ1-p平面分成8个区域(见图2)。

根据奇异性理论，参数在同一个区域内取值时，幅频响应的定性特征是保持不变的，因而分别从不同区域内取一组(ζ1,p)值，画对应的分岔曲线，就可以得到参数变化时所有不同类型的分岔图(见图3)，共有8种，同时利用升-降龙格库塔法进行了相应的数值计算(图3中星号)。

当参数(ζ1,p)的值在图2“区域1”选择时，系统幅频响应曲线与图3(a)定性相同，非线性未起作用，属于完全线性响应。

当参数(ζ1,p)位于图2“区域2”时，幅频响应曲线类同于图3(b)，非线性起作用，出现孤立解，且若主弹簧阻尼比ζ1为定值，随着外激励幅值p的增加，孤立解演变成封闭的独立环，并逐渐扩大。

当参数(ζ1,p)位于图2“区域3”时，幅频响应曲线类同于图3(c)，第一段解曲线越过约束位置，向独立环靠拢。

当参数(ζ1,p)位于图2“区域4”时，第一段解曲线在约束位置的上方，与独立环连通，且在连接位置附近的左右支有多解共存现象(见图3(d))。

当参数(ζ1,p)位于图2“区域5”时，第一段解曲线在约束位置线上，与独立环连通，且在连接位置附近的左右支也有多解共存现象(见图3(e))，其分岔图与区域4的比较，两段解连通的位置发生了变化。

当参数(ζ1,p)位于图2“区域6”时，系统滞后性减弱，此时只有右支还存在滞后性(见图3(f))。

当参数(ζ1,p)位于图2“区域7”时，其分岔图与区域6的比较，边界点与极限点的相对位置发生了变化(见图3(g))。

当参数(ζ1,p)位于图2“区域8”时，系统滞后性消失，整体呈现拟线性(见图3(h))。

综合以上分析可见，与文献[10-12]采用垂直斜坡图形标准法相比，分岔分析的奇异性方法更简便，并能得到更丰富的信息。

工程中为避免跳跃现象引起机械设备性能突变甚至破坏，就须在非跳跃区选择系统参数，也就是说在区域1和区域8内选择参数是避免跳跃的有效措施。

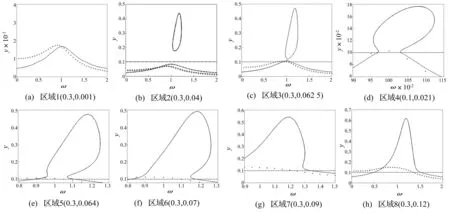
图3　分岔图 Fig.3 Diagram of bifurcation

3定常解的稳定性分析

(12)

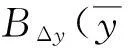
(13)

(14)

(15)

展开行列式得

(16)

于是，定常解的失稳条件为

(17)

不等式(17)可以判断定常解的稳定性，如果幅频响应在不稳定区域则会出现跳跃现象。由于非线性振动存在不稳定区域，所以在进行参数选择时，应使得系统不存在不稳定区域，或者不稳定区域尽量少。下面分别讨论系统为非线性振动时，参数ζ1、ζ2、k对不稳定区域的影响(见图4)。

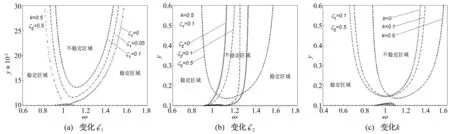
图4　参数ζ 1、ζ 2、k对系统稳定区域的影响 Fig.4 The influence of parameters ζ 1、ζ 2、k on unstable region

图4(a)表明，主弹簧阻尼比ζ1越大，则不稳定区域越小。

图4(b)表明，随着副弹簧阻尼比ζ2的逐渐增大，不稳定区域先减小后增大，且从一个不稳定区域变为两个。

图4(c)表明，随着刚度系数的逐渐增大，不稳定区域增大且慢慢向右移动。

4隔振效果分析

隔振效果的好坏通常用力传递率Tf来表示，它定义为通过隔振装置传递到基础上的力幅值与作用于振动系统上的激励力的幅值之比。由式(3)和式(6)可知传递到基础上的动荷载为

(18)

式中：

(19)

于是，传到基础上最大的动荷载值为

(20)

非线性系统的力传递率为

(21)

隔振系统设计的目标就是选择合理的隔振器参数，即刚度系数和阻尼系数，使得传递到基础上的力最小，达到降低振动传递与噪声抑制的作用。当系统处于非线性振动时，在奇异性分析的基础上，以刚度系数和阻尼系数作为设计变量，分别变化参数ζ1、ζ2、k得到相应的Tf曲线(见图5)。

图5(a)所示，随着主弹簧阻尼比ζ1的增加，共振区的力传递率峰值迅速升高，且传递率曲线出现了独立环。

图5(b)所示，随着副弹簧阻尼比ζ2的增加，共振区的力传递率峰值迅速降低，且发现阻尼比的影响逐渐减弱。

图5(c)所示，刚度系数k的增加，对低频和高频区的力传递率都没有影响，对共振区有影响，此时共振峰逐渐增大，且峰值向右移，使得共振频率发生了轻微改变。

由此可知，当系统处于非线性振动时，刚度和阻尼等参数主要影响共振区的隔振效果，线性阻尼和刚度系数的增加都将减弱系统的隔振效果，而非线性阻尼系数的增加能加强隔振效果；同时传递率曲线与幅频曲线具有同步的多解现象，例如在图5(a)中ζ1=0.3情况下的传递率曲线与图3(b)中所对应的幅频曲线在相同的参数下均出现了孤立环。

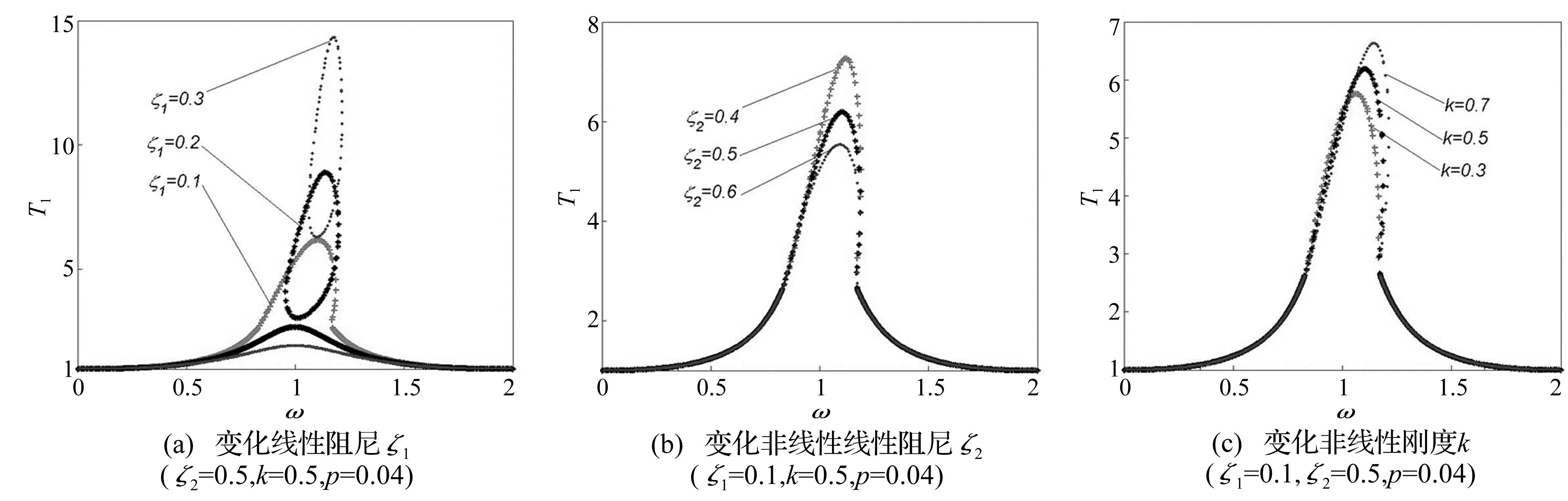
图5　参数ζ 1、ζ 2、k对T f的影响 Fig.5 The influence of parameters ζ 1、ζ 2、k on T fcurve

5结论

本文利用平均法理论、约束分岔理论分析了对称的分段线性弹簧系统的主共振响应，得到以下结论：

(1)利用约束分岔理论定性地分析系统可能发生的响应类型，并获得系统不同参数下丰富的振动特性；

(2)根据李雅普诺夫一次近似稳定性理论对系统主共振定常解的稳定性进行了分析，结果表明随着阻尼系数的变化，不稳定区域的范围也将变化，而刚度系数则影响不稳定区域的位置；

(3)当系统含非线性阻尼时，线性阻尼的增加反而减弱隔振效果，此时只有非线性阻尼能加强隔振。

参考文献

[1]罗冠炜，张艳龙，谢建华. 含对称刚性约束振动系统的周期运动和分岔[J]. 工程力学学报,2007,24(7):44-52.

LUO Guan-zhong,ZHANG Yan-long,XIE Jian-hua.Periodic-impact motions and bifurcations of vibratory systems with symmetrical rigid constraints[J].Journal of engineering mechanics,2007, 24(7):44-52.

[2]吴志强，丁然，陈予恕. 约束含参分岔问题的分类[J]. 应用数学和力学,2010(2): 127-133.

WU Zhi-qiang, DING Ran，CHEN Yu-shu. Classification of bifurcations for nonlinear dynamical problems with constraints[J]. Applied Mathematics and Mechanics, 2010，31(2)：127-133.

[3]王林泽，赵文礼. 外加正弦驱动力抑制一类分段光滑系统的混沌运动[J]. 物理学报,2005(9): 4038-4043.

WANG Lin-ze, ZHAO Wen-li.Suppression of chaotic motion in a class of piecewise-smooth systems by using sine periodic force[J].Acta Physica Sinica,2005(9): 4038-4043.

[4]Luo G W, Xie J H. Codimension two bifurcation of periodic vibro-impact and chaos of a dual component system[J]. Physics Letters A,2003, 313: 267-273.

[5]Luo G W, Chu Y D, Zhang Y L. Codimension two bifurcation of a vibro-bounce system[J]. Acta Mechanica Sinica,2005, 21(2): 197-206.

[6]方益奇，王克军，张明，等. 分段线性减振系统的振动性能分析[J]. 机械科学与技术,2011，30(2): 251-255.

FANG Yi-qi, WANG Ke-jun,ZHANG Ming, et al. An analysis of vibration performance of piecewise linear vibration-reduction system[J]. Mechanical Science and Technology, 2011，30(2)：251-255.

[7]徐得元，唐国安. 限位弹性-阻尼元件设计及隔振效果研究[J]. 上海航天,2012, 29(3): 42-48.

XU De-yuan, TANG Guo-an. Design and vibration isolationstudy of elastic damping element with displacement restriction[J].Aerospace Shanghai,2012, 29(3): 42-48.

[8]吴志强，陈予恕. 含约束非线性动力系统的分岔分类[J]. 应用数学和力学,2002(5): 477-482.

WU Zhi-qiang,CHEN Yu-shu. Classification of bifurcations for nonlinear dynamical problems with constraints[J]. Applied Mathematics and Mechanics, 2002，23(5)：477-482.

[9]陈予恕. 非线性振动系统的分叉和混沌理论[M]. 北京：高等教育出版社，1993.

[10]Jazar G N, Mahinfalah M, Deshpande S. Design of a piecewise linear vibration isolator for jump avoidance[J]. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics,2007, 221(3): 441-449.

[11]Jazar G N, Houim R, Narimani A, et al. Frequency response and jump avoidance in a nonlinear passive engine mount[J]. Journal of Vibration and Control,2006, 12(11): 1205-1237.

[12]Deshpande S, Mehta S, Jazar G N. Jump avoidance conditions for piecewise linear vibration isolator[C]. 2005.