地震动频谱特性对隔震结构响应及损伤影响研究

第一作者杜东升男，博士，副教授，1976年生

邮箱：ddshy@163.com

地震动频谱特性对隔震结构响应及损伤影响研究

杜东升，王曙光，刘伟庆，李威威

(南京工业大学土木工程学院，南京210009)

摘要：针对地震动复杂频谱特性对隔震结构响应及损伤影响进行研究，用加速度反应谱平均周期Tr表征地震动周期特性，用Bouc-Wen模型及刚度退化的Bouc-Wen模型分别描述隔震层与上部楼层的滞变特性，建立隔震结构的质点系非线性分析模型，考虑隔震支座压剪相关性与拉压性能差异建立隔震体系损伤指数模型，分析不同地震动输入加速度幅值及不同Tr与对隔震结构地震反应、损伤影响规律。分析表明，在地震动高频范围内隔震结构响应随输入加速度峰值增加而增加，但对长周期地震动，输入加速度峰值对隔震结构地震反应影响较小，地震反应呈较大离散性、无规律性；在相同加速度幅值输入下隔震层地震反应、损伤的离散性远大于上部结构，在共振区内虽出现最大地震反应，但也会出现较小地震反应，表明隔震结构瞬时共振为非常复杂的过程。研究可为揭示地震动特性与隔震结构地震反应及损伤的关联性提供分析依据。

关键词：频谱特性；隔震结构；反应谱平均周期；损伤

基金项目：江苏省前瞻性联合研究项目(BY2015005-14);国家自然科学基金项目(51178219)

收稿日期：2013-11-08修改稿收到日期：2014-09-18

中图分类号:TU352.1

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.20.034

Abstract:The nonlinear characteristics of a base isolated structure and the time-variation of excitation frequency on it make the effect of earthquake ground motion on structural responses and damages very complicated. The average period Tr of response spectrum was used to represent the cyclical nature of earthquake ground motion. The base isolated structure was simplified to a two-mass model, and the Bouc-Wen model and the stiffness degradation of Bouc-Wen model were used to simulate the hysteresis of isolation story and superstructure respectively. Referring to the Park-Ang damage index model and considering the compression-shear correlation and tension-compression difference of isolators, the damage index model of the isolated structure was established. The nonlinear seismic responses and damages of the structure under earthquake ground motion with different Tr were analyzed. The results show that the seismic response and damage both increase with the increase of acceleration peak of seismic wave in the range of high frequency, but the seismic response is of discreteness and irregularity under long period seismic wave. The discreteness of seismic response of isolation layer is larger than that of sup-structure. In resonance region, there may appear the highest seismic response, but it is also possible to see a rather lower seimic response, which indicates that the instantaneous resonance of isolated structure is a complex phenomenon. The study reveals the characteristics of earthquake ground motion and the resulted seismic responses and damages of base isolated structures.

Influences of spectral characteristics of earthquake ground motion on seismic responses and damages of base isolated structures

DUDong-sheng,WANGShu-guang,LIUWei-qing,LIWei-wei(College of Civil Engineering，Nanjing University of Technology，Nanjing 210009，China)

Key words:spectral characteristic; base isolated structure; average period of response spectrum; damage

目前对地震动频谱特性研究已有丰富成果[1-5]，但不同频谱特性地震动对结构地震响应及非线性损伤影响规律尚无较系统研究，在地震作用下隔震结构随位移变化其自振频率亦不断变化，致该影响更复杂。

地震动是地震工程与工程抗震间的桥梁[6]，深入研究地震动特性是研究结构地震响应机理的前提，但地震响应大多与地震动特性有关。地震动特性研究目前主要围绕地震动传播影响因素及地震动自身特性进行，且主要集中于震源、地质构造环境、传播介质及场地条件对地震动特性影响，对地震动自身特性研究主要针对其幅值特性[7-8]、谱值特性[9-12]及时频特性[13-16]。该研究成果作为工程结构动力性能与抗震减灾理论基础[17]，但结合地震动特性与结构响应机理研究尚少[18]，主要集中于长周期地震动与近场速度脉冲型地震动对结构响应影响。翁大根等[19]针对上海地区软体特性将反应谱影响曲线延长至10 s以适应建筑的抗震设计；川崎恵[20]在长周期地震动对建筑地震响应、损伤评估进行初步研究，利用各层塑性率、累计塑性率分析高层建筑在长周期地震动及标准地震动作用下的不同影响；陈清军等[21]研究长周期地震波作用下高层建筑结构的弹塑性动力响应表明，长周期地震动对高层结构位移响应影响更大，且会使高层结构损伤更严重；地震动特性对隔震结构地震响应影响研究集中于地震动长周期特性对隔震建筑影响，如Minagawa等[22]利用半主动控制方法设计出“Super-Long-Period Active Isolation System”规避共振风险，但需较大控制力，难以实现；Kitamura等[23]进行长周期地震动作用下隔震建筑抗震性能评估研究，假定东京、大阪地区遭遇超过设防的长周期地震动时评估隔震建筑抗震性能，包括地震能量积累、损耗、隔震层最大位移响应等。

本文研究隔震结构在不同幅值特性、频率特性输入地震动作用下非线性地震反应，分析随输入地震动加速度峰值及周期不断增加隔震结构地震响应变化规律。由于缺乏描述隔震层损伤模型，提出能考虑隔震层压剪相关及拉压性能不同的隔震层损伤模型，并研究不同地震动幅值、频谱特性对隔震结构损伤的影响规律。

1地震动频率特性描述及地震动选取

地震动频谱特性描述尚无成熟方法，常以5%阻尼比加速度反应谱卓越周期Tg反映地震动频谱特征，但地震波的Tg较难给出确定值，而对傅里叶振幅谱，虽能能检出地震动时程中所有频率特征，但无法从中提取能准确代表地震动频率成份的稳定值。因此需找到稳定性更好的频谱参数确定地震动频率取值。Rathje等[24]通过对地震动频谱参数深入研究，提出地震动周期的4种表达方法，其中较常用的即为加速度反应谱平均周期Tr与反应谱卓越周期To。其表达式分别为

(1)

(2)

式中：Ti为5%阻尼比加速度反应谱等间距离散周期；Sa(Ti)为Ti对应的谱加速度；PGA为峰值加速度。

式(1)限定计算周期范围为0.02～10 s，可满足对地震动长周期段研究需求及模拟式强震仪、数字强震记录有足够信噪比要求。Tr为对地震动一定频段范围内频谱特性表征，其计算周期范围包括长周期，可反映地震动长周期分量对其贡献，且能由反应谱角度考察地震动频谱参数；式(2)要求Ti取值范围为Sa(Ti)/PGA≤1.2。因该两评价地震动频率特性指标各有适用的频率范围，分析中同时采用。

对地震动特性研究需可靠的宽频数字记录及排除各种因素间相互影响，对强震记录仪器及地震数量、规模均有严格要求。本文所用地震动主要源自日本防灾科学技术研究所(NIED)K-net、KIK-net地震数据库与美国太平洋地震工程中心(PEER)地震动数据库。采用不同频率特性的1996条地震动，Tr范围涵盖0.04～3.76 s，部分地震动信息见表1。

表1　部分地震动详细信息

部分典型的不同周期地震动加速度时程曲线及地震波动力放大系数曲线见图1。由图1可看出地震动的不同频谱特性。由于幅值过小的地震动对非线性结构影响难以体现，故在分析所选地震动均加速度幅值大于70 gal。

2地震动频谱特性对隔震结构响应影响

隔震结构为典型的强非线性结构，非线性主要体现在隔震层的非线性，故隔震层滞变恢复力模型为建立隔震结构振动控制方程的关键因素。本文用Bouc-Wen模型描述隔震层滞回特性，表达式为

(3)

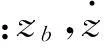
图1　不同频谱特性典型地震波时程及动力放大系数曲线 Fig.1 Acceleration history curves and dynamic magnification factor of typical seismic wave with different spectral characteristics

考虑隔震结构上部结构在循环往复荷载作用下强度、刚度退化，采用能较好反映滞变力退化过程的滞变位移微分方程，即

(4)

式中：Al，ν，η均为累积滞变耗能函数，并据滞回耗能确定结构退化程度。

利用隔震层及上部结构滞回特性描述方法可建立隔震结构振动控制方程，即

(5)

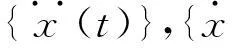
式中：kb，αb为隔震层一、二次刚度系数；k1～kj，α1～αj为上部各层一、二次刚度系数。

将位移、速度及滞变位移共同形成状态空间，建立隔震结构状态方程，即

(6)

采用四阶龙格-库塔方法求解式(6)，可解出不同幅频特性地震动作用下隔震层及上部结构加速度及位移反应。不同加速度峰值地震动作用下隔震层及上部结构加速度反应见图2。由图2看出，输入地震动峰值及隔震层加速度响应峰值相关性较小，即大加速度峰值输入未必获得大反应， 3.8 m/s2加速度输入的隔震层响应为9.6 m/s2输入的近2倍，故用调整峰值加速度方法获得一致输入水平至少对隔震结构设计不太合理，而上部结构加速度响应及输入加速度峰值相关性较好，相关系数达0.832，可能因上部结构非线性程度较小所致。

输入地震动峰值与隔震结构位移间关系见图3。由图3看出，二者相关性不大，随输入地震动峰值增加位移响应有减小趋势，可能因峰值在(0.8～2.0) m/s2间地震波数量较多频率较丰富所致。

隔震层动力放大系数随地震动反应谱平均周期Tr变化见图4。由图4看出，在地震动高频范围内，随Tr增加隔震层动力放大系数基本呈增加趋势，Tr<1 s时隔震层动力放大系数绝大部分均小于0.6，说明隔震结构隔震效果较好；而对长周期地震动隔震效果明显减小，最大动力放大系数甚至达到0.93，且在地震动长周期范围内隔震结构动力放大系数离散性较大。由图中隔震结构在地震作用下随变形而变化的周期范围看出，即便在可能出现共振区间内，隔震结构动力放大系数离散性也较大，虽在该区段内出现最大地震反应，但也会出现较小地震反应，故隔震结构的瞬时共振为较复杂过程。上部结构动力放大系数随Tr变化除数值稍有增加外规律与隔震层基本一致。

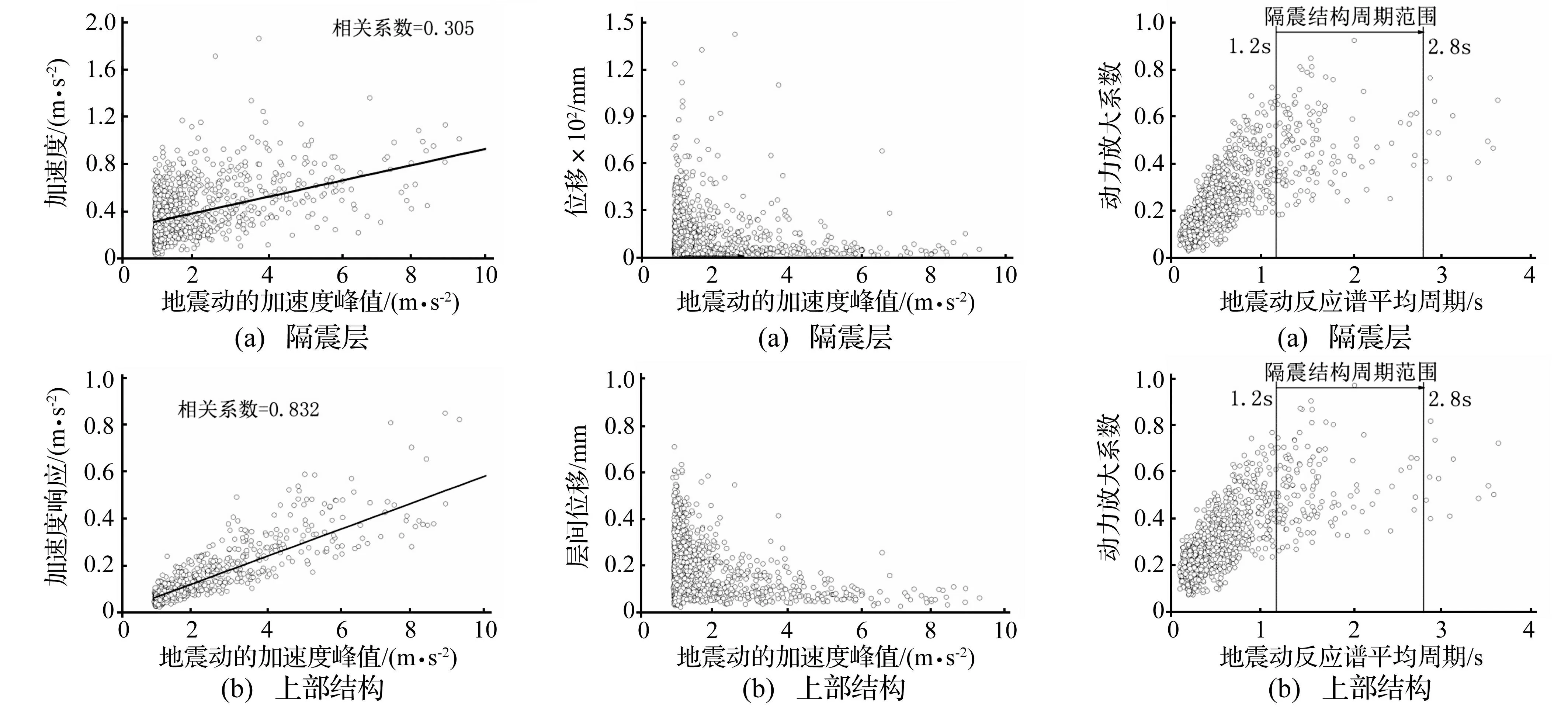
图2 隔震结构加速度反应与地震动加速度峰值关系Fig.2AccelerationresponseofISwithdifferentpeakofearthquakegroundmotion图3 隔震结构位移反应与地震动加速度峰值关系Fig.3RelationshipbetweenthepeakaccelerationanddisplacementofIS图4 地震动反应谱平均周期与隔震结构动力放大系数关系Fig.4DynamicmagnificationfactorofISwithTr

图5　隔震层、上部结构层间位移随T r变化 Fig.5 Isolation layer displacement and sup-structure drift with T r

隔震层位移及上部结构层间位移随Tr的变化见图5。由图5看出，隔震层位移在Tr<1 范围内接近线性增长，但地震动长周期变化非常剧烈，隔震层最大位移达142 mm，最小位移仅0.38 mm，相差近370倍。在隔震结构周期范围内隔震层位移虽整体增大，但随Tr的变化规律不明显，需进一步结合地震动时频分布进行分析。隔震结构上部层间位移随Tr的变化基本类似，但数值小很多。

由以上分析知，隔震结构的地震反应同时受地震动幅值特性、频率特性影响。隔震层加速度、位移反应与地震动加速度峰值、反应谱平均周期关系三维曲面见图6。由图6看出，在地震动高频范围内，隔震结构响应随输入加速度峰值增加而增加，但对长周期地震动，输入加速度峰值对隔震结构地震反应影响较小，地震反应离散性较大且无规律性。

3地震动频谱特性对隔震结构损伤影响

目前常用构件或结构的地震损伤模型为Park等提出的地震弹塑性变形与累积滞变耗能线性组合地震损伤模型，较符合结构在罕遇地震作用下的损伤情况，表示为

(7)

式中：Di为地震作用下结构第i层损伤指数；δmaxi为第i层最大位移；δui为单调加载下第i层极限变形；Qyi为第i层屈服强度；∑Ei为第i层累计滞回耗能；β为非负常数，本文取0.2[25]。

对隔震结构，该模型无法反映其压剪相关性对隔震层损伤影响及隔震支座拉压特性差异及支座的受拉损伤，而此两方面均为影响隔震层损伤必须考虑的，在Park-Ang损伤模型基础上综合隔震层弹塑性变形与累积滞变耗能，提出隔震层损伤模型，即

(8)

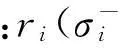
该模型为三参数的损伤指数模型，能较完整的体现出影响隔震层损伤各种因素。

不同加速度峰值地震动作用下隔震层及上部结构损伤指数见图7。由图7看出，地震动加速度峰值与隔震结构损伤指数相关性较小，基本无明确规律，而地震动加速度峰值与上部结构损伤指数相关性稍大，随加速度峰值增加损伤呈增加趋势。

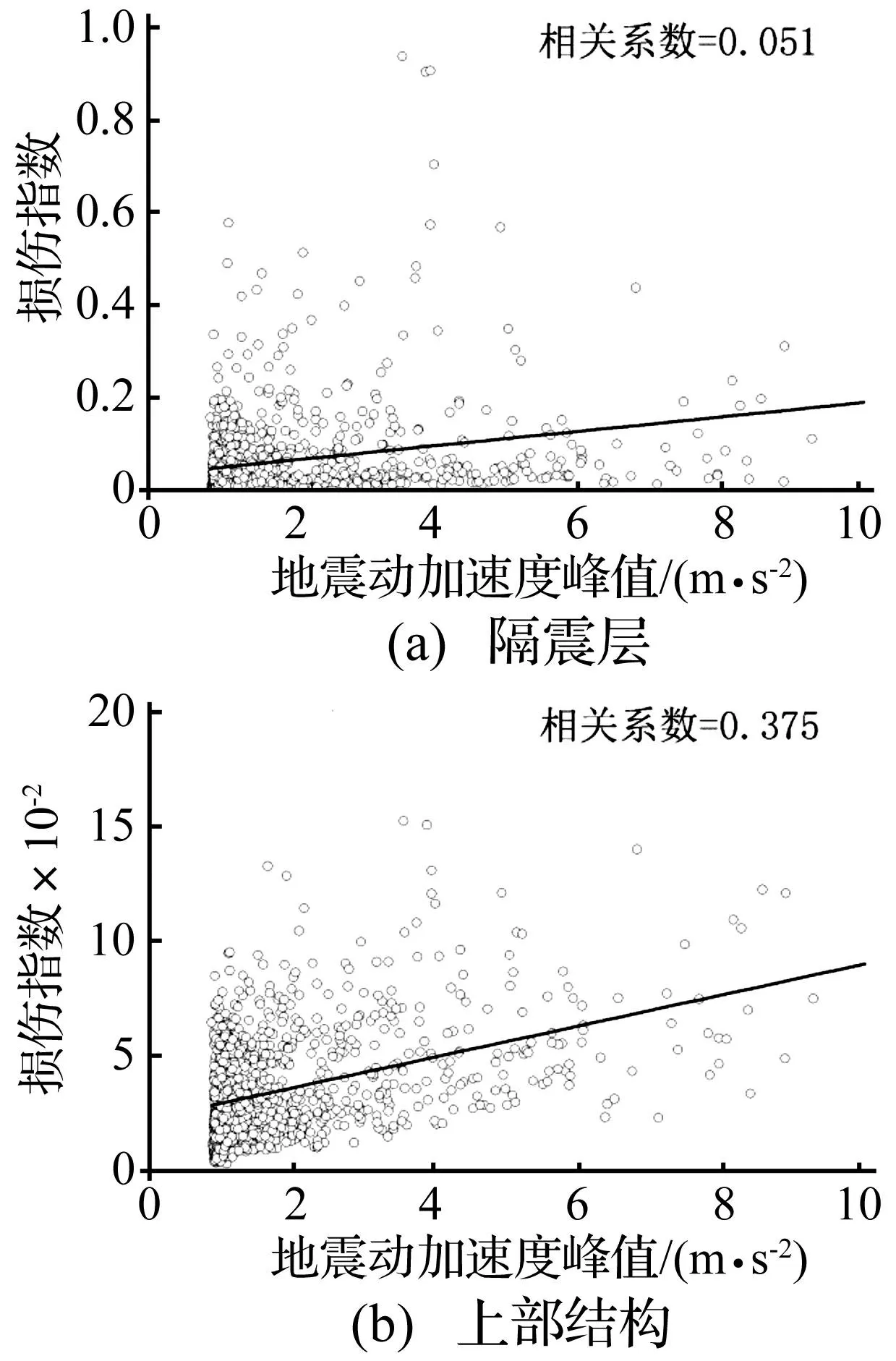
图7　隔震结构损伤指数与地震动加速度峰值关系 Fig.7 Damage index IS with different peak of earthquake ground motion

隔震结构损伤指数随Tr变化见图8。由图8看出，与地震反应类似，隔震层损伤指数在高频地震动作用下离散性较小，而在长周期地震动作用下隔震层损伤呈较大离散性、无规律性，上部结构损伤因子随Tr增加而增加趋势明显。

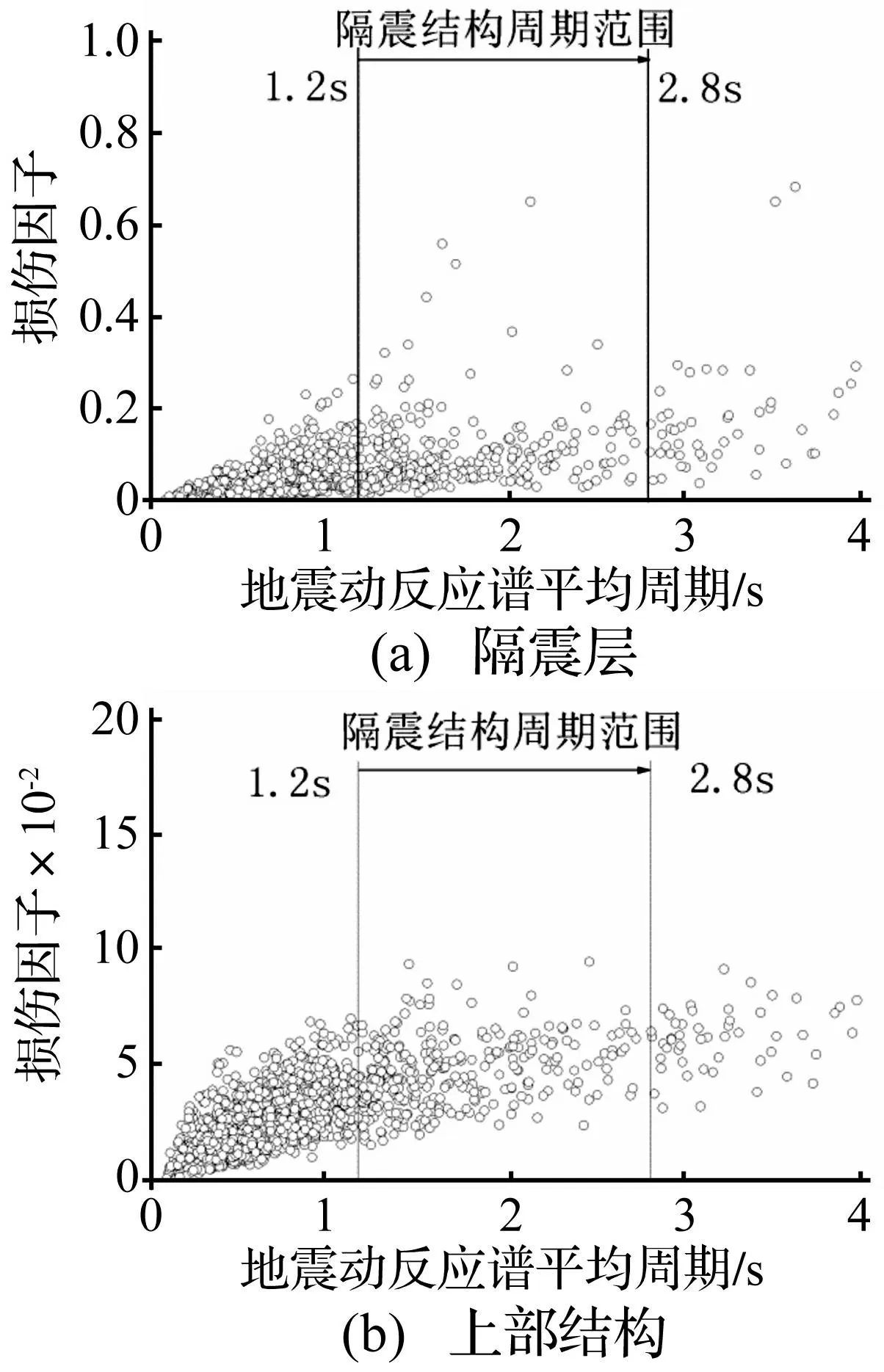
图8　隔震结构损伤指数与地震动反应谱平均周期关系 Fig.7 Damage index IS with average period of acceleration response spectrumT r

4结论

本文用地震动反应谱平均周期表征地震动频率特性，建立隔震结构的非线性分析模型与损伤指数模型，研究地震动幅值特性与频率特性对隔震结构非线性地震反应及损伤影响，结论如下：

(1)输入地震动峰值、隔震层加速度响应峰值及损伤指数的相关性较小，设计中用调整峰值加速度方法获得一致的输入水平对隔震结构设计不太合理，而上部结构加速度响应及输入加速度峰值相关性较好。

(2)在地震动高频范围内，随Tr增加隔震层动力放大系数基本呈增加趋势，在Tr<1 s范围内，隔震层动力放大系数绝大部分均小于0.6，说明对高频地震动隔震结构隔震效果较好，而对长周期地震动隔震效果减小明显。

(3)在可能出现共振区间内，隔震结构动力放大系数离散性较大，不仅会出现最大地震反应，也会出现较小地震反应；地震动高频范围内，隔震结构响应随输入加速度峰值增加而增加，但对长周期地震动，输入加速度峰值对隔震结构地震反应影响较小，地震反应离散性较大且无规律性。

(4)隔震层损伤指数在高频地震动作用下离散性较小，而在长周期地震动作用下隔震层损伤会呈较大离散性、无规律性，但上部结构损伤因子随Tr增加有较一致的增加趋势。

参考文献

[1]李小军,彭青,刘文忠. 设计地震动参数确定中的场地影响考虑[J]. 世界地震工程,2001,17(4):34-41.

LI Xiao-jun, PENG Qing, LIU Wen-zhong. Consideration of site effects for determination of design earthquake ground motion parameters[J]. World Information On Earthquake Engineering, 2001,17(4):34-41.

[2]陈培善，Duda S J. 峰值速度和加速度对环境剪应力的依赖性[J]. 地球物理学报,1993,36:185-194.

CHEN Pei-shan, Duda S J. Dependence of peak acceleration and peak velocity on the environment shear stress[J]. Chinese Journal of Geophysics, 1993，36:185-194.

[3]Joyner W B, Boore D M. Measurement, characterization and prediction of strong ground motion[C]//Proc Conf on Earthquake Eng. and Soil Dynamics Ⅱ，GT Div/ASCE，Park City，Utah,June 27-30,1988.

[4]Campbell K W, Bozorgnia Y. Empirical analysis of strong ground motion from the 1992 landers, california, earthquake[J]. Bull Seism Soc Amer,1994,84:573-588.

[5]Somerville P G. Magnitude scaling of the near fault rupturedirectivity pulse.[J] Phys Earth Planet Inter. 2003,137: 201-212.

[6]胡聿贤.地震工程学(2版)[M].北京:地震出版社, 2006.

[7]Schnabel P B.Accelerationson rock for earthquakes in the western united states[J]. BSSA, 1972,63(2): 501-516.

[8]郝敏,谢礼立. 集集地震等震线和PGA、PGV等值线关系的研究[J].地震工程与工程振动,2006,26(1):18-21.

HAO Min,XIE Li-li. Study on the relationship between isoseismal and isolines of PGA and PGV for Chi-Chi Earthquake[J]. Earthquake Engineering and Engineering Vibration,2006,26(1):18-21.

[9]Abrahamson N A, Silva W J. Empirical response spectral attenuation relations for shallow crustal earthquakes[J]. Seismol. Res. Lett.,1997, 68 (1):94-127.

[10]Sadigh K, Chang C Y, Egan J A, et al. Attenuation relationships for shallow crustal earthquakes based on California strong motion data[J].Seismol.Res. Lett.,1997,68 (1):180-189.

[11]Rathje E M, Abrahamon N A,Bray J D.Simplified frequency content estimates of earthquake ground motions [J]. Journal of Geotechnical and Geoenvironmental Engineering,1998(2):150-159.

[12]Rathje E M,Faraj F, Russell S. Empirical relationships for frequency content parameters of earthquake ground motions[J]. Earthquake Spectra, 2004,20(1):119-144.

[13]Yeh C H, Wen Y K. Modeling of nonstationary ground motion and analysis of inelastic structural response[J]. Struct. Safety,1990, 8(1/2/3/4):281-298.

[14]Papadimitriou C. Stochastic characterization of strong ground motion and applications to structural response[C]//Rep. No. EERL 9003, California Inst. of Technol., Pasadena, Calif.,1990.

[15]Conte J P. Effects of earthquake frequency nonstationarity on inelastic structural response[C]// Proc., 10th World Conf. on Earthquake Engrg., A. A. Balkema, Rotterdam, The Netherlands,1992.

[16]Conte J P, Peng B F. Fully nonstationary analytical earthquake ground-motion model[J]. Journal of Engineering Mechanics, 1997, 123(1):15-24 .

[17]李杰,李国强. 地震工程学导论[M]. 北京:地震出版社, 1992.

[18]王博,白国良,代慧娟.典型地震动作用下长周期单自由度体系地震反应分析[J].振动与冲击,2013,32(15):190-196.

WANG Bo,BAI Guo-liang,DAI Hui-juan.Seismic response analysis of long-period SDOF system under typical ground motions[J].Journal of Vibration and Shock,2013, 32(15): 190-196.

[19]翁大根,徐植信. 上海地区抗震设计反应谱研究[J]．同济大学学报,1993,21(1):9-16.

WENG Da-gen XU Zhi-xin. A study on seismic design spectrum for shanghai area[J].Journal of Tongji University (Natural Science),1993,21(1):9-16.

[20]川崎恵. 長周期地震動に対する鋼構造超高層建物の損傷評価[R]．日本建築学会大会学術講演梗概集, 2007.

[21]陈清军,袁伟泽,曹丽雅. 长周期地震波作用下高层建筑结构的弹塑性动力响应分析[J]. 力学季刊, 2011,32(3): 403-408.

CHEN Qing-jun, YUAN Wei-ze, CAO Li-ya. Elasto-plastic dynamic response analysis of high rise structures under long period ground motion[J]. Chinese Quarterly of Mechanics, 2011,32(3):403-408.

[22]Minagawa K, Fujita S. Fundamental study on the super-long-period active isolation system [J]．Journal of Pressure Vessel Technology November,2006, 128:135-141.

[23]Kitamura H, Takenaka Y, Tamura K. Seismic performance of seismic-isolated building for long-period ground motion and limited performance of seismic isolator [J]．ASCE Conf. Proc., 2008,315:1-12.

[24]Rathje E M, Abrahamson N A, Bray J D. Simplified frequency content estimates of earthquake ground motions [J]. J. Geotech. Eng. Div., Am. Soc. Civ. Eng.,1998,124 (2): 150-159.

[25]Bertero R D, Bertero V V. Performance-based seismic engineering: the need for a reliable conceptual comprehensive approach[J]. Earthquake Engineering and Structural Dynamics,2002, 31(3): 627-652.