电路量子电动力学系统中的几何相位门制备

电路量子电动力学系统中的几何相位门制备

张英俏

( 延边大学理学院 物理系, 吉林 延吉 133002 )

摘要：利用电路量子电动力学系统中传输线并联等离子振荡量子比特与共振器的色散耦合，提出了一个制备几何相位门的方案,方案中的相位门制备能在量子比特衰变和退相干之前完成,因此本文方案具有可行性.

关键词：几何相位门; 电路QED; 传输线并联等离子振荡量子比特

收稿日期：2014-11-03

基金项目：吉林省科技发展计划青年科研基金资助项目(20130522148JH)；延边大学科技发展项目(延大科合字[2012]第14号)

文章编号：1004-4353(2015)02-0142-03

中图分类号：O431

Generation of a geometric phase gate in circuit QED

ZHANG Yingqiao

(DepartmentofPhysics,CollegeofScience,YanbianUniversity,Yanji133002,China)

Abstract：A scheme to generate a geometric phase gate is proposed in circuit quantum electrodynamics (QED) based on transmons dispersively coupled to a transmission line resonator (TLR). Gate generation can be finished before the relaxation and dephasing of the qubits, which ensures the feasibility of the proposed scheme.

Key words： geometric phase gate; circuit QED; transmon

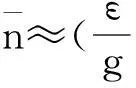
基于色散耦合模型，本文利用传输线并联等离子振荡量子比特与共振器的相互作用提出了一个制备几何相位门的方案.利用当前的实验技术,方案中要求的色散极限条件很容易得到满足,保证了方案的可执行性.

1基于色散相互作用的几何相位门制备

几何相位的相关知识见文献[14].在Tavis-Cummings模型[15]中,两个传输线并联等离子振荡量子比特与共振器的耦合系统的哈密顿可由式(1)给出：

(1)

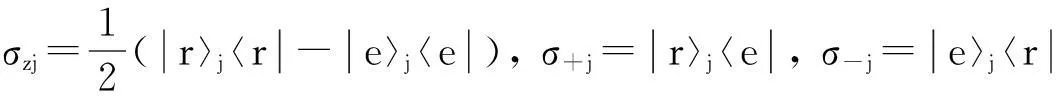
在频率为ωL=ω的脉冲驱动下,共振器的哈密顿为[13]

HII=ε(t)(a†e-iωLt +aeiωLt ),

(2)

其中ε(t)是外部驱动场的振幅.当高Q共振器在大振幅驱动场条件下时,方程(2)中的哈密顿可写成[13]

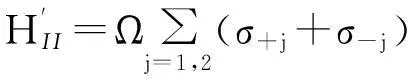
(3)

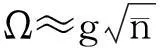
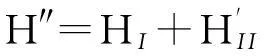
(4)

以共振器频率ωr为框架进行旋转可得

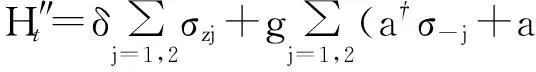
(5)

其中δ=ω-ωr.在色散极限条件δ≫Ω,g下,传输线并联等离子振荡量子比特与共振器之间虽没有能量交换,但仍然存在色散耦合且有效哈密顿为

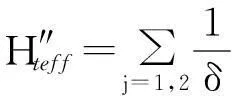
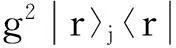
(6)

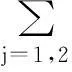
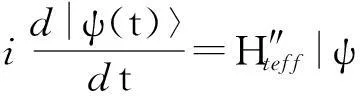
(7)

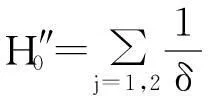
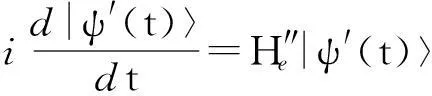
(8)

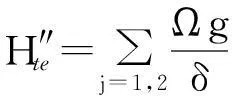
(9)

(10)

基于位移算符D″(dα″)可以获得经过无限短的时间间隔dt″后的演化算符为

U″(dt″)=D″(dα″)=ea†dα″-adα″*=e-iH″edt″ ,

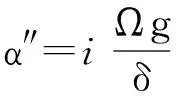
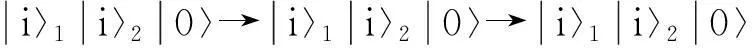
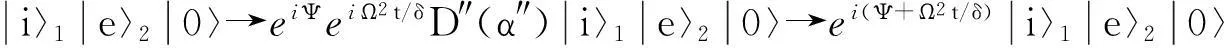
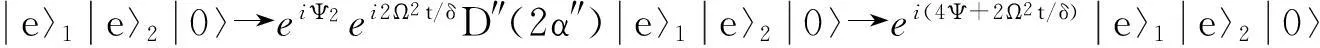
(11)

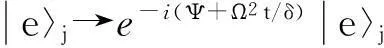
(12)

在制备过程中需满足条件(-ωr+g2/δ)t=2π和2Ψ=-π.

2结果与讨论

本文方案是通过调节每个量子比特近端的磁通偏压线来改变其跃迁频率的，根据文献[8-10]的实验结果,量子比特的跃迁频率可通过控制每个量子比特线圈的磁通来实现静态调节，也可以利用偏压线产生的电压偏差以及可自调频率的共振器[17]实现频率调节.此外，还有一种不需要额外调节任何参数的方法，但需要射频驱动振幅更加稳健的共振器,该方法常常产生较慢的逻辑门.

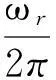
由以上讨论可知，本文提出的利用传输线并联等离子振荡量子比特与共振器的色散耦合制备几何相位门的方案，其门制备时间远小于量子比特的弛豫时间和退相干时间，能够保证方案在有效时间内完成，且该方案还适用于多比特情况.

参考文献：

[1]Yamamoto T, Pashkin Yu A, Astafiev O, et al. Demonstration of conditional gate operation using superconducting charge qubits[J]. Nature, 2003,425:941-944.

[2]Majer J B, Paauw F G, ter Haar A C J, et al. Spectroscopy on two coupled superconducting flux qubits[J]. Phys Rev Lett, 2005,94:090501(4).

[3]Hime T, Reichardt P A, Plourde B L T, et al. Solid-state qubits with current-controlled coupling[J]. Science, 2006,314:1427-1429.

[4]Berkley A J, Xu H, Ramos R C, et al. Entangled macroscopic quantum states in two superconducting qubits[J]. Science, 2003,300:1548-1550.

[5]Wallraff A, Schuster D I, Blais A, et al. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics[J]. Nature, 2004,431:162-167.

[6]You J Q, Hu X D, Ashhab S, et al. Low-decoherence flux qubit[J]. Phys Rev B, 2007,75:140515(R)(4).

[7]Koch J, Yu T M, Gambetta J, et al. Charge-insensitive qubit design derived from the Cooper pairbox[J]. Phys Rev A, 2007,76:042319(19).

[8]Majer J, Chow J M, Gambetta J M, et al. Coupling superconducting qubits via a cavity bus[J]. Nature, 2007,449:443-447.

[9]Leek P J, Filipp S, Maurer P, et al. Using sideband transitions for two-qubit operations in superconducting circuits[J]. Phys Rev B, 2009,79:180511(R)(4).

[10]DiCarlo L, Chow J M, Gambetta J M, et al. Demonstration of two-qubit algorithms with a superconducting quantum processor[J]. Nature, 2009,460:240-244.

[11]Wu C W, Han Y, Li H Y, et al. Fast quantum phase gate in a small-detuning circuit QED model[J]. Phys Rev A, 2010,82:014303(4).

[12]Wu C W, Han Y, Zhong X J, et al. One-way quantum computation with circuit quantum electrodynamics[J]. Phys Rev A, 2010,81:034301(4).

[13]Blais A, Gambetta J, Wallraff A, et al. Quantum-information processing with circuit quantum electrodynamics[J]. Phys Rev A, 2007,75:032329(21).

[14]张英俏.基于传输线并联等离子振荡量子比特制备几何受控相位门[J].延边大学学报:自然科学版,2013,39:256-259.

[15]Walls D F, Milburn G J. Quantum Optics[M]. 2nd ed. Berlin: Springer-Verlag, 2008.

[16]Zheng S B. Unconventional geometric quantum phase gates with a cavity QED system[J]. Phys Rev A, 2004,70:052320(4).

[17]Wallquist M, Shumeiko V S, Wendin G. Selective coupling of superconducting charge qubits mediated by a tunable stripline cavity[J]. Phys Rev B, 2006,74:224506(10).