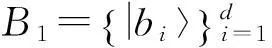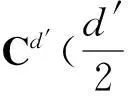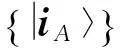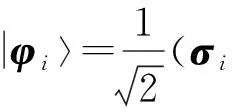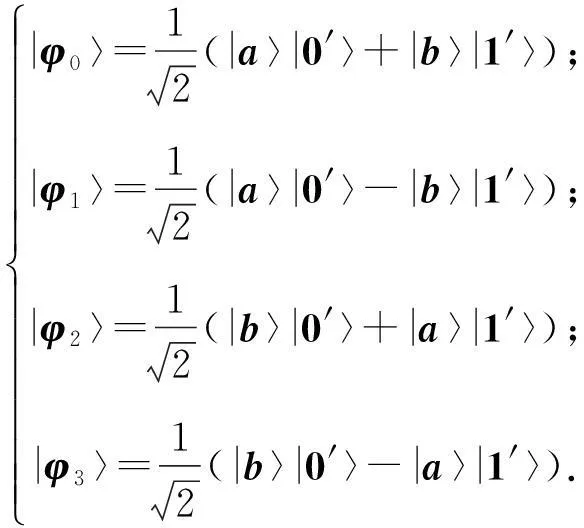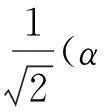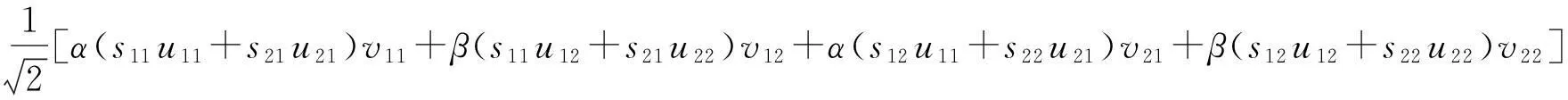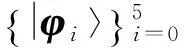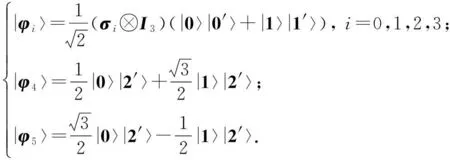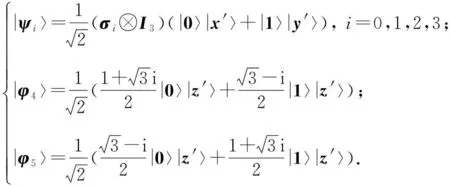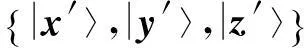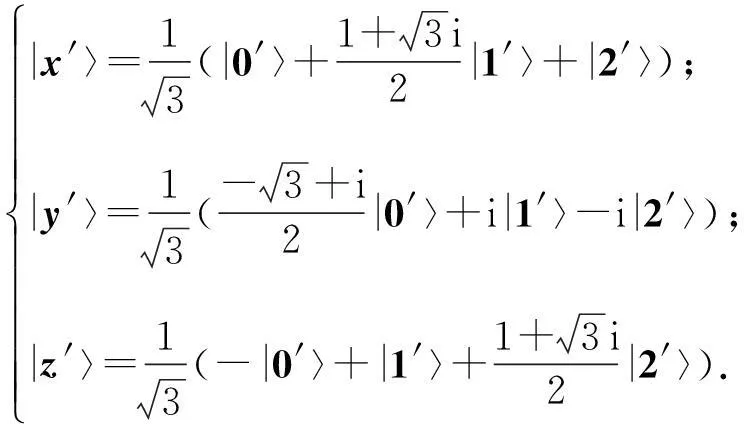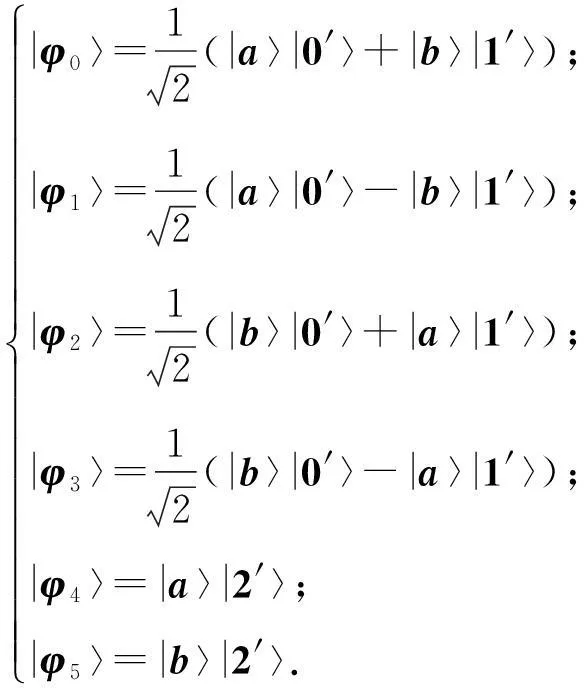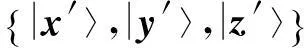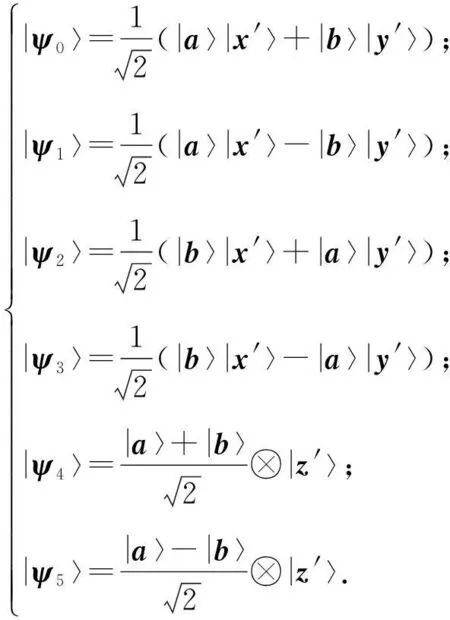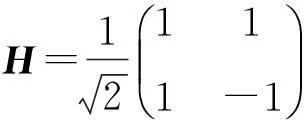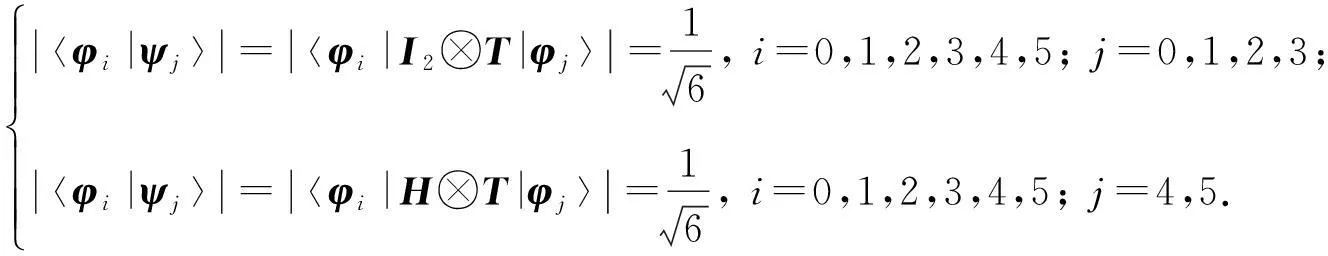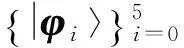量子系统C2⊗C3中无偏的不可扩展最大纠缠基的新构造

量子系统C2⊗C3中无偏的不可扩展最大纠缠基的新构造

卜繁强1，杨强2，陶元红2*

( 1.延边朝鲜族自治州学校后勤服务中心， 吉林 延吉 133000； 2.延边大学理学院 数学系, 吉林 延吉 133002 )

摘要：讨论量子系统C2⊗C3中无偏的不可扩展最大纠缠基的新构造.首先选取空间C2中的任意规范正交基，构造出C2⊗C3中一类4-成员的不可扩展的最大纠缠系统，然后再通过添加C2⊗C3中的两个规范正交向量将其扩充成C2⊗C3中的基底；其次通过变换C3空间的基底，构造出C2⊗C3中另一组完全不同的不可扩展的最大纠缠基，并讨论这两组基无偏的充分必要条件.

关键词：无偏基； 最大纠缠态； 不可扩展的最大纠缠基

收稿日期：2015-05-14*通信作者： 陶元红(1973—)，女，博士，副教授，研究方向为泛函分析及应用.

基金项目：国家自然科学基金资助项目(11361065)；吉林省自然科学基金资助项目(201215239)

文章编号：1004-4353(2015)02-0136-06

中图分类号：O177.3

New construction of mutually unbiased unextendible maximally entangled bases in quantum systemC2⊗C3

BU Fanqiang1,YANG Qiang2,TAO Yuanhong2*

( 1.SchoolLogisticsServiceCenterofYanbianKoreanAutonomousPrefecture,Yanji133000，China；

2.DepartmentofMathematics,CollegeofScience,YanbianUniversity,Yanji133002,China)

Abstract：New constructions of mutually unbiased unextendible maximally entangled bases in quantum system C2⊗C3 are discussed. Firstly, by choosing an arbitrary orthonormal basis in C2, we construct a kind of 4-member unextendible maximally entangled system in C2⊗C3, which becomes an unextendible maximally entangled basis in C2⊗C3 after we add two orthonormal vectors in C2⊗C3. Secondly, through changing the basis of C3, another unextendible maximally entangled basis is established, and the sufficient and necessary conditions of mutually unbiaseness of them are discussed.

Key words： mutually unbiased bases; maximally entangled state; unextendible maximally entangled basis

在量子系统Cd⊗Cd中，n-成员的不可扩展的最大纠缠基[1]是由n(n

2013年，陈斌等[8]构造了量子系统C2⊗C3中的4-成员的不可扩展的最大纠缠系统：

(1)

定理1如下4个向量可以构成C2⊗C3中一组不可扩展的最大纠缠系统：

(2)

α〈1|(StU)|0〉〈1′|V|0′〉+β〈1|(StU)|1〉〈1′|V|1′〉)=

α(s11u11+s21u21)v11+β(s11u12+s21u22)v12+α(s12u11+s22u21)v21+β(s12u12+s22u22)v22=0.

(3)

同理，由〈φi|ψ〉=0,i=1,2,3可得如下3个方程：

α(s11u11+s21u21)v11+β(s11u12+s21u22)v12-α(s12u11+s22u21)v21-β(s12u12+s22u22)v22=0,

(4)

α(s11u11+s21u21)v21+β(s11u12+s21u22)v22+α(s12u11+s22u21)v11+β(s12u12+s22u22)v12=0,

(5)

-α(s11u11+s21u21)v21-β(s11u12+s21u22)v22+α(s12u11+s22u21)v11+β(s12u12+s22u22)v12=0.

(6)

显然,式(3)—(6)可写成如下矩阵形式:

(7)

即为齐次方程组:

Bλ=0,

(8)

s11u11+s21u21=s11u12+s21u22=s12u11+s22u21=s12u12+s22u22=0.

综上，式(2)中的4个向量构成了C2⊗C3中的一组不可扩展的最大纠缠系统.

2C2⊗C3中不可扩展的最大纠缠基的无偏构造

本文基于C2⊗C3中式(2)这一组不可扩展的最大纠缠系统，可以填补两个规范正交向量使其成为C2⊗C3的一个基底，这两个规范正交向量可以是C2⊗C3中的直积态，也可以是非最大纠缠的纠缠态，只要保证与式(2)中所有的向量分别正交即可.不妨先给式(2)填补C2⊗C3中两个最容易构造的规范正交直积态，构成量子系统C2⊗C3中如下不可扩展的最大纠缠基：

(9)

(10)

显然，

(11)

根据以上分析可得

(12)

参考文献：

[1]BravyiS,SmolinJA.Unextendiblemaximallyentangledbases[J].PhysRevA, 2011,84:042306.

[2]WoottersWK,FieldsBD.Optimalstate-determinationbymutuallyunbiasedmeasurements[J].AnnPhys, 1989,191:363-381.

[3]EnglertBG,AharonovY.Themeanking’sproblem:primedegreesoffreedom[J].PhysLettA, 2001,1:284.

[4]Fernandez-PerezA,KlimovAB,SaavedraC.Quantumprocessreconstructionbasedonmutuallyunbiasedbasis[J].PhysRevA, 2011,83:052332.

[5]AdamsonRBA,SteinbergAM.Improvingquantumstateestimationwithmutuallyunbiasedbases[J].PhysRevLett, 2010,105:030406.

[6]YuLC,LinF,HuangCY.Quantumsecretsharingwithmultilevelmutually(un)biasedbases[J].PhysRevA, 2008,78:012344.

[7]CerfNJ,BourennaneM,KarlssonA,etal.Securityofquantumkeydistributionusingd-levelsystems[J].PhysRevLett, 2002,88:127902.

[8]ChenB,FeiSM.Unextendiblemaximallyentangledbasesandmutuallyunbiasedbases[J].PhysRevA, 2013,88:034301.

[9]李玮，林平，郑鸿楠，等.2×3量子系统中互不偏的不可扩展最大纠缠基[J].延边大学学报：自然科学版，2014,40(2):109-113.

[10]杨强，陶元红，张军,等.C2⊗C3中无偏的不可扩展最大纠缠基[J].哈尔滨理工大学学报，2014,19(4):84-87.

[11]杨强,陶元红,南华,等.C2⊗C3中Bell基型不可拓展的最大纠缠基和互不偏基[J].吉林大学学报：理学版，2015，53(5)：547-552.

[12]NizamidinH,MaT,FeiSM.AnoteonmutuallyunbiasedunextendiblemaximallyentangledbasesinC2⊗C3[J].IntJTheorPhys, 2015,54:326-333.