非交换无色散 Gelfand-Dickey 方程族的附加对称

胡美艳,李传忠

（宁波大学 数学与统计学院,浙江 宁波 315211）

无色散可积系统(KP、Toda 等)是低维可积场中的重要系统,主要应用于数学、物理、拓扑场、矩阵模型等领域[1-2].无色散可积系统的构造是将经典可积系统中的算子和李括号替换为相位函数和泊松括号,可以看成是经典可积系统的一种形变或类似.类似经典的可积系统,无色散可积系统具有许多优良的性质,如Lax 对、无穷守恒量和对称性[3-4]等.近年来,附加流显式形式的附加对称性[5-7]引起了广泛关注.20 世纪80 年代,Orlov 等[5]给出了构造无穷多可积非线性演化方程附加对称性的一般方法.20 世纪90 年代,Leur[8]研究了KdV型方程族的弦方程和W1+∞约束,Takasaki 等[1-4]研究了无色散的可积方程族(KP、Toda).21 世纪以来,Wang[9]和Li[7]分别对非交换KP 和GD 方程族的附加对称做了研究,Wang 等[10]也研究了无色散非交换KP 方程族的多哈密顿结构.本文利用类似的方法研究非交换无色散GD 方程族的附加对称.

1 预备知识

在非交换可积系统的研究中,玛雅代数[11-13]发挥着极其重要的作用,其中玛雅乘积⋆的定义为:

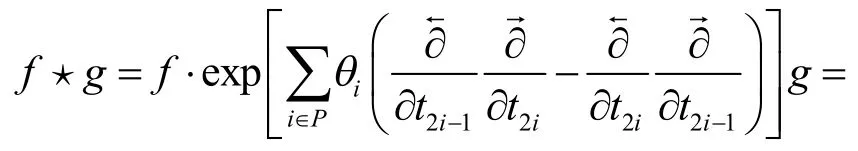
式中:P表示一组有限整数;t2i-1,t2i(i∈P)是非交换坐标;θi表示非交换参数;ϑ(θ2)表示高阶项.当θi→0时,非交换系统将被简化为交换系统.

非交换无色散GD方程族的Lax函数L 定义为:

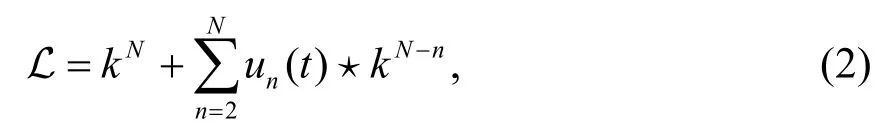
其中u=u(x,t1,t2,…).非交换无色散GD 方程族的Lax 方程为:

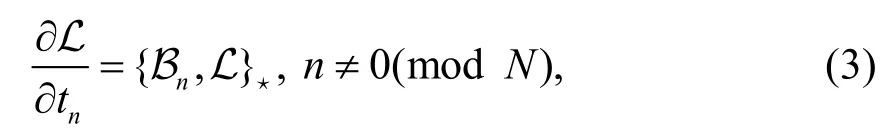
N=2时,L=k2+u2是非交换无色散KdV方程族的Lax 函数,其中包含非交换无色散KdV方程

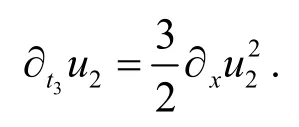
N=3时,非交换无色散Boussinesq 方程族的Lax 函数是 L=k3+u2k+u3,相应的非交换无色散Boussinesq 方程为:

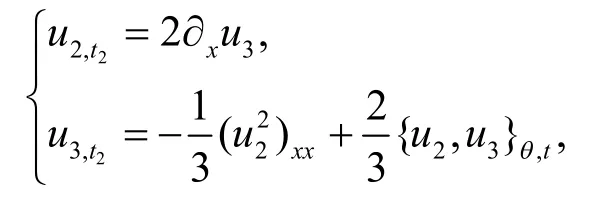
非交换无色散GD 方程族的Lax 函数也可以表示为:

其中dressing 函数φ满足

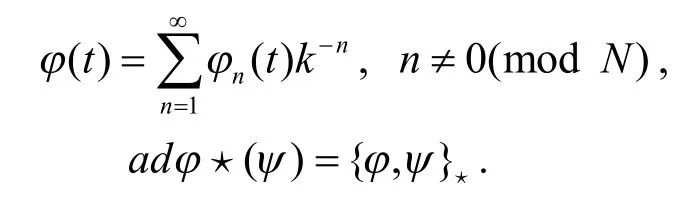
另外,式(3)等价于下述Sato 方程:

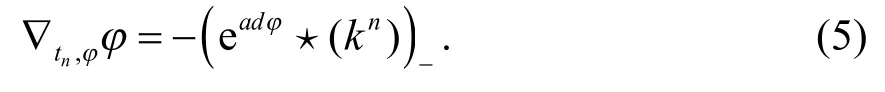
为了方便研究非交换无色散GD 方程族的附加对称,引入Orlov-Schulman 函数Μ,假定函数

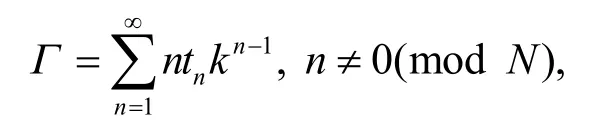
同时将Orlov-Schulman 函数Μ 定义为:

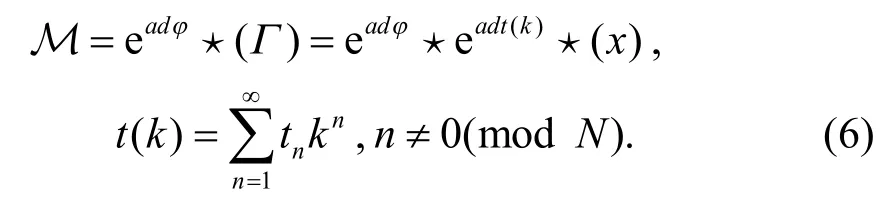
进一步计算,函数Μ 也可以用Lax 函数L 表示:

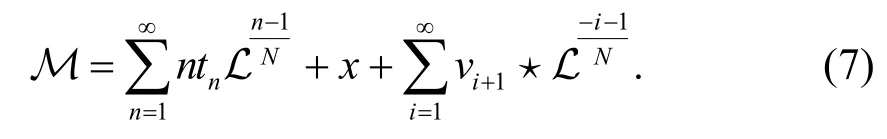
性质1函数Μ 满足下列等式:

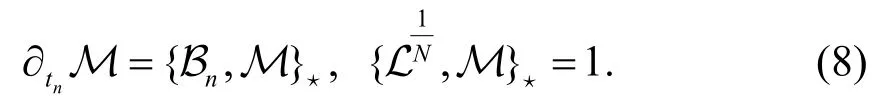
证明先证明第二个结论,

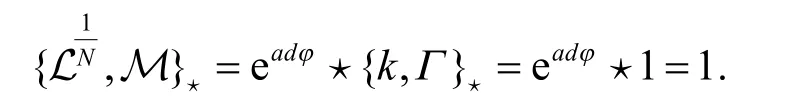
根据 ∂(eadY⋆X)=eadY⋆(∂X)+{∇YY,eadY⋆(X)}⋆,对方程(6)进行计算,

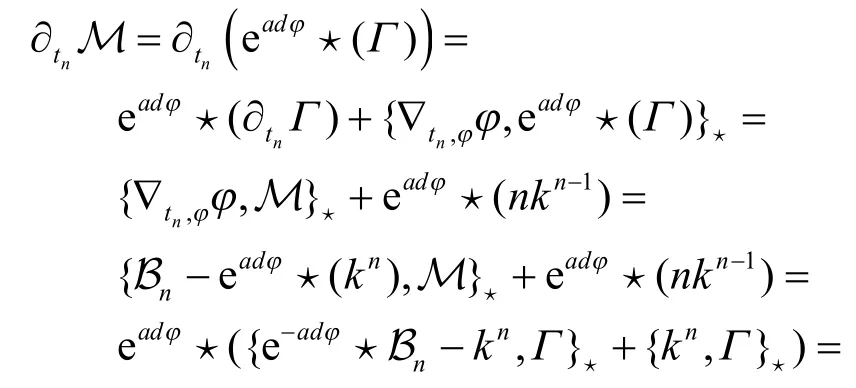
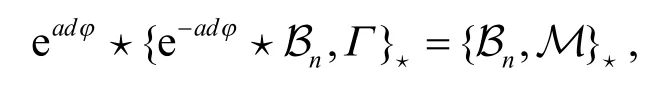
即为所求,证毕.

2 附加对称

首先给出非交换无色散GD方程族的附加对称.

定义1微分方程

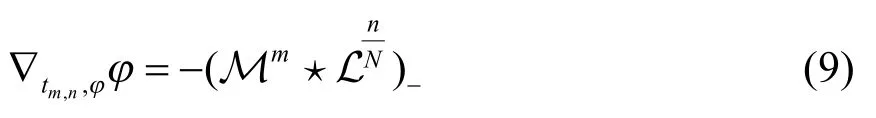
有了上述准备,现在来定义附加流,并且证明这些流是对称的.类似于无色散KP 方程族的情形,引入附加变量并且定义作用在函数L 和Μ 上的附加流为:

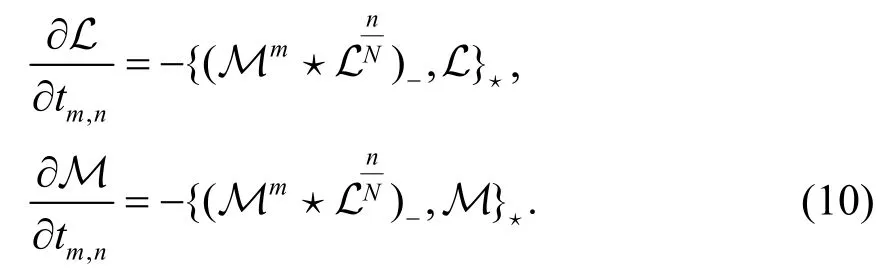
定理1在非交换无色散GD 方程族中,只有满足条件的附加流存活.

证明对于非交换无色散GD 方程族的Lax 函数(2)而言,它的负部等于0.根据式(10)有

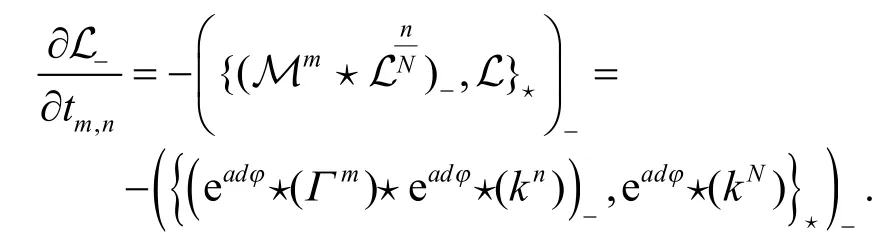
经过一系列计算,上述等式还可以写为:

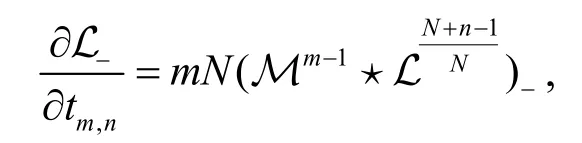
另外,非交换无色散GD 方程族中存活的附加流也有一些很重要的性质.

性质2在非交换无色散GD 方程族中,附加流和原始流交换,即,n≠0(modN).

证明将上式两边作用在Lax函数L 上,运用方程(3)和(10)有

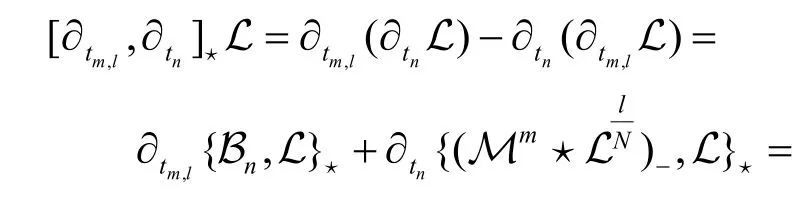
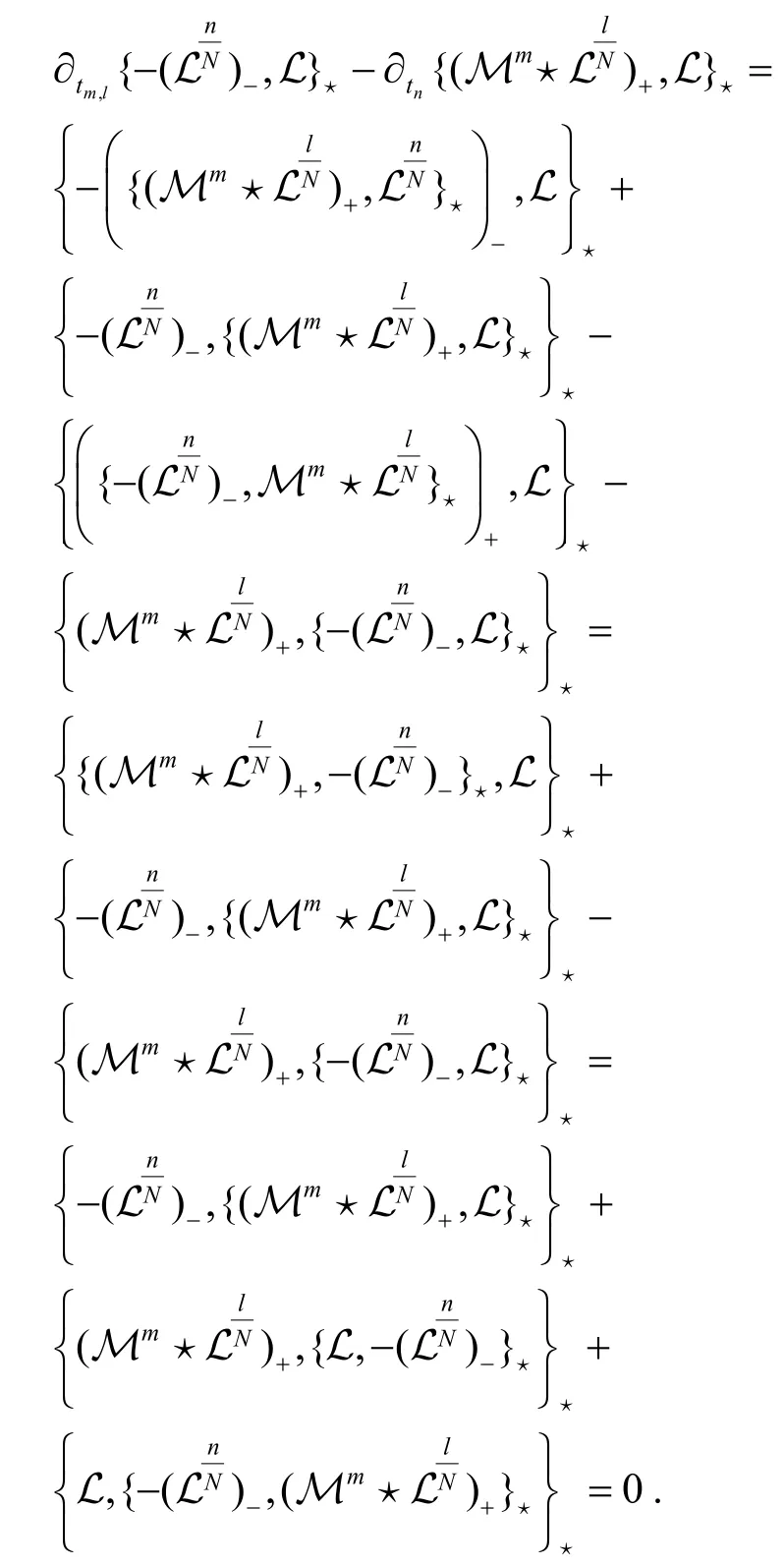
性质3非交换无色散GD 方程族的附加流可以形成无中心的 W1+∞代数.

证明直接计算可以得到

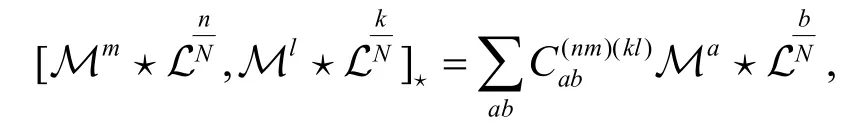
这意味着

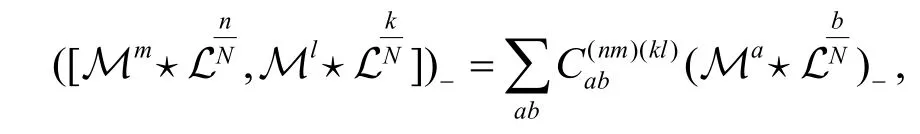
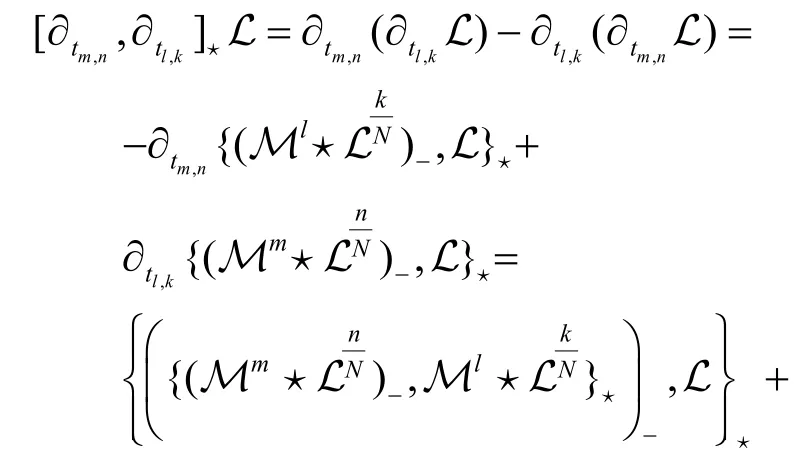
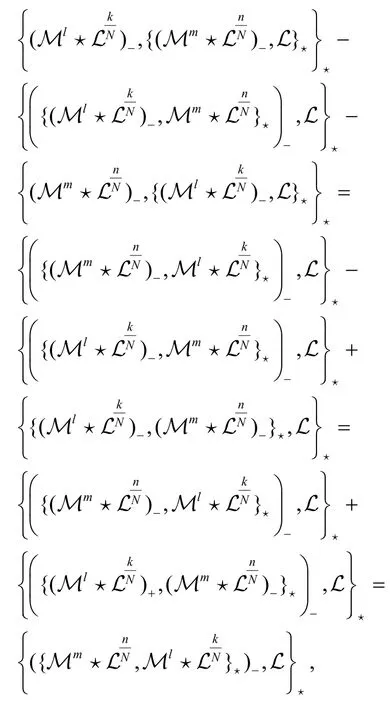
也就是说

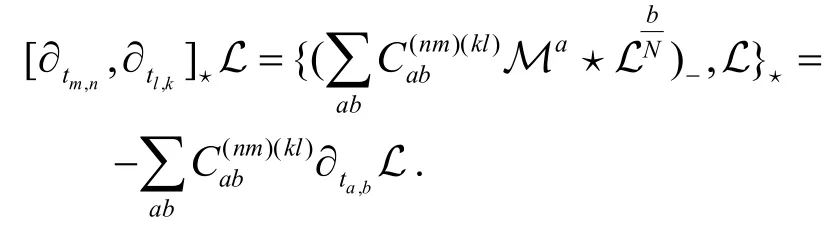
3 弦方程

本节在非交换无色散GD 方程族附加对称的基础上,给出它的弦方程.

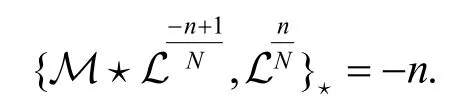
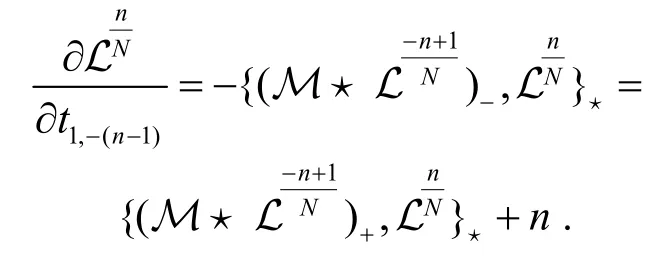
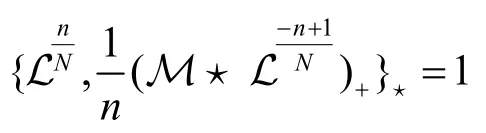
就是非交换无色散GD 方程族的弦方程.从上述推导中可以看出弦方程是指函数与附加变量无关的条件,即.

4 总结

本文主要研究非交换无色散GD 方程族的附加对称及存活的附加流的性质.由于该方程族Lax函数的特殊性,只有满足条件的附加流存活,这是与非交换无色散KP 方程族的一大不同.通过特殊附加流作用,得到弦方程.