一类具有未建模动态的非线性系统的稳定性研究

一类具有未建模动态的非线性系统的稳定性研究

石啊莲1,任舒翼2

( 1.齐鲁师范学院 数学学院, 山东 济南 250013； 2.山东广播电视大学 公共基础教学部, 山东 济南 250014 )

摘要：研究了一类具有未建模动态的非线性系统的稳定性问题.针对系统的不确定性，首先设计一状态观测器，对系统的全部状态进行估计；然后基于Lyapunov稳定性理论，采用Backstepping方法设计了输出反馈自适应控制器；最后证明了控制器在原点处平衡，可使系统的信号一致有界或者渐近收敛，且仿真举例验证了本文方法的有效性.

关键词：非线性系统; 未建模动态； Backstepping方法; 自适应控制

收稿日期：2015-05-24

作者简介：石啊莲(1983—)，女，讲师，研究方向为非线性控制.

文章编号：1004-4353(2015)02-0116-08

中图分类号：O231.2

Stability of a class of nonlinear systems with unmodelled dynamics

SHI Alian1，REN Shuyi2

( 1.DepartmentofMathematics,QiluNormalInstitute，Jinan250013,China;

2.DepartmentofPublicBasicTeachingofShandongTVUniversity,Jinan250014,China)

Abstract：We studiy the stability of a class of nonlinear systems with unmodelled dynamics. In view of uncertainty of the system, a state observer is introduced firstly to estimate all the states of the system; then based on the Lyapunov stability theory, the output-feedback adaptive controller is designed by using the backstepping method. Furthermore, we prove that the controller keeps equilibrium at origin. It can make all signals of the system are uniformly bounded or asymptotic convergence. An illustrative example is proposed to verify its effectiveness.

Key words： nonlinear system; dynamics uncertainties; Backstepping; adaptive control

通常未建模动态的存在使得实际系统的控制效果不佳，会产生不稳定的现象，所以对未建模动态进行处理很有必要[1-4].文献[5]研究了一类具有未建模动态的非线性系统，用动态信号控制系统的动态不确定性，在系统有界的前提下，提出了一种有效的自适应控制方法.文献[6]引入一可测动态信号来克服未建模动态，并提出了一种鲁棒自适应控制的新方法.文献[7]针对具有未建模动态的非线性系统，提出了一种鲁棒Backstepping控制方法.文献[8]针对一类具有未建模动态和随机干扰的系统，采用控制定位、持续辨识系统建模以及随机分析等方法对其进行了研究.基于上述研究，本文对一类含有未建模动态的非线性系统进行了输出反馈控制设计，所设计的控制器能实现闭环系统的所有信号一致有界或渐近收敛.

1系统描述及问题假设

考察非线性系统：

(1)

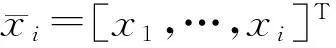
假设y=x1可测,其余状态分量都不可测,则系统(1)可改写为矩阵方程组：

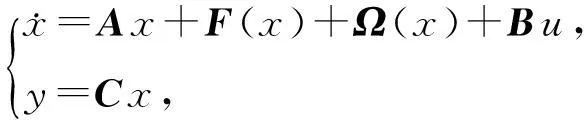
(2)

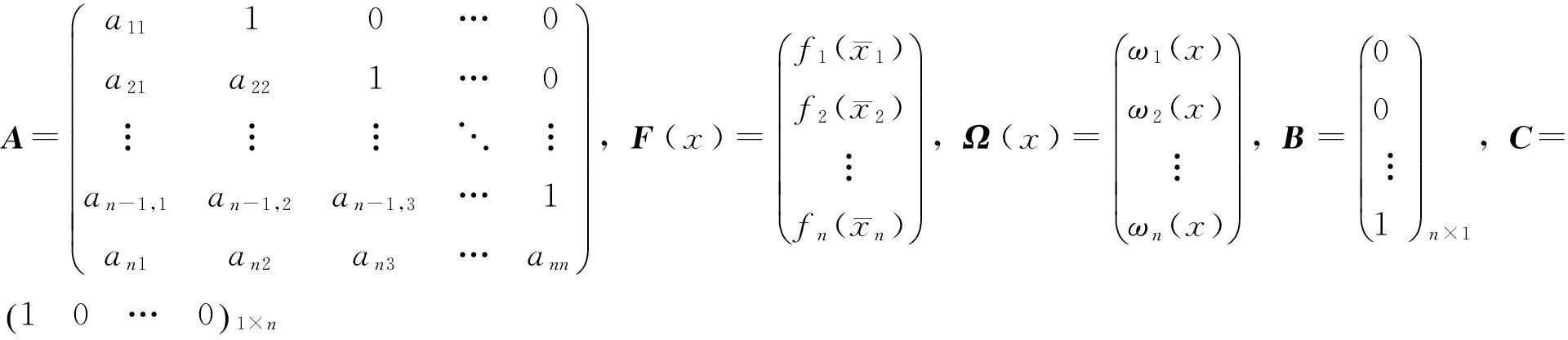
针对系统的未建模动态特性，本文通过设计一个稳定的控制器使系统(1)渐近稳定.首先对F(x)和Ω(x)进行如下假设:

(H1)F(·)已知且充分光滑,且有F(0)=0.

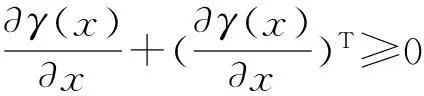
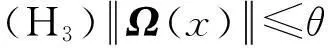
根据以上假设，本文对参数θ进行估计,以使闭环系统渐近稳定.

2控制器的设计

首先引入观测器

(3)

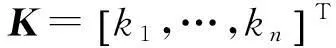
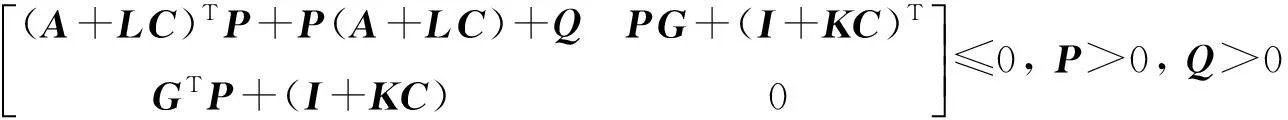
(4)

(5)

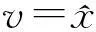
首先引入引理：

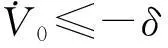
(6)

这里φ(y)≥0为光滑函数,δ>0, Θ≥0为常数.

证明记μ=x-v,由(H2)知F(x)-F(v)=G(γ(x)-γ(x-μ))Gφ(x,μ),这里

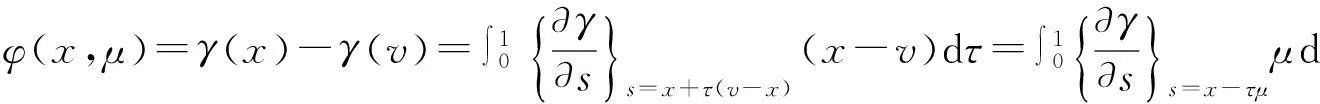
(7)

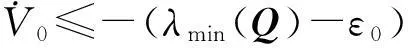
(8)

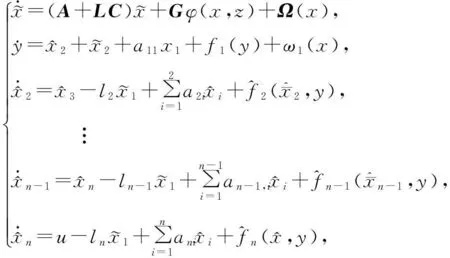
(9)

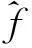
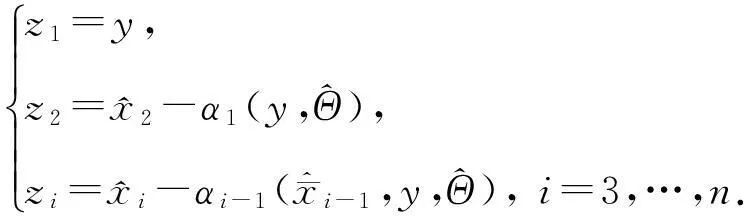
(10)

(11)

(12)

(13)

利用配方原理有

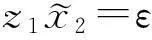
(14)

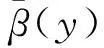
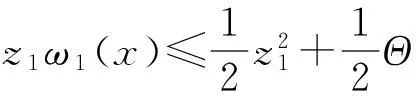
(15)

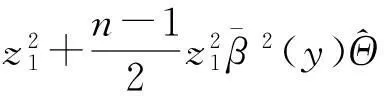
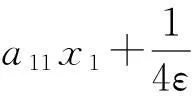
选取虚拟控制器α1为

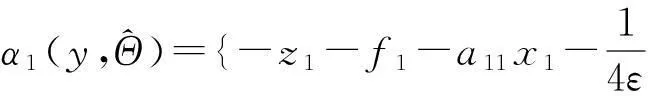
(16)

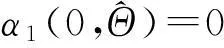
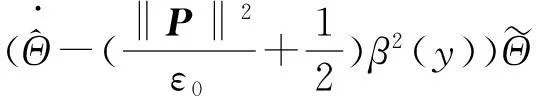
第i步(i=3,…,n)同理,选择虚拟控制器

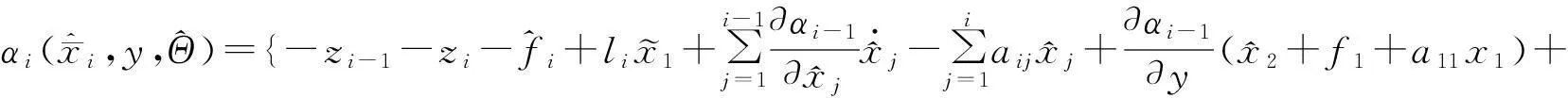
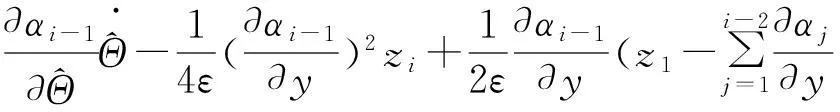
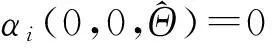
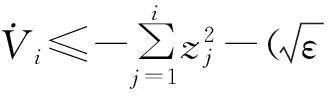
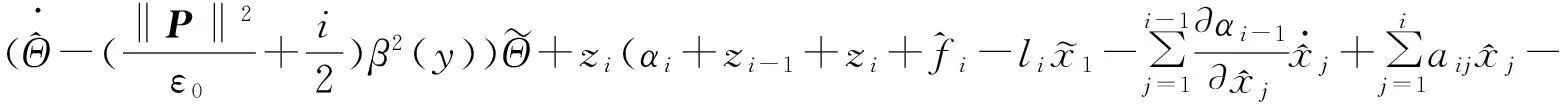
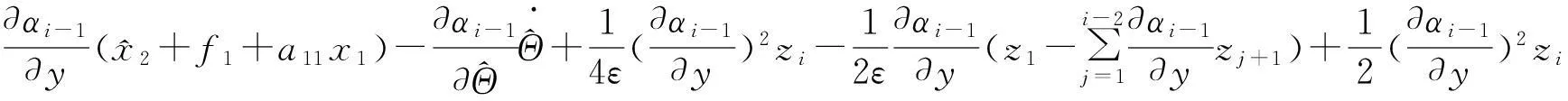
第n步当i=n时上面第i步的结论也成立,因此可设计如下实际控制器:

(17)

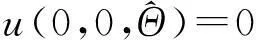
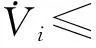
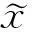
(18)

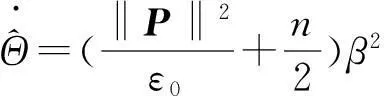
(19)

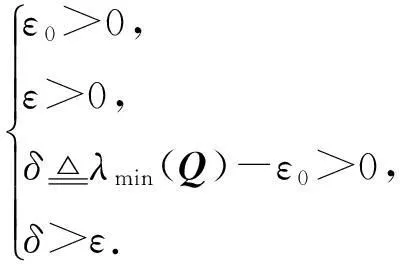
(20)

由于Q正定,因此λmin(Q)>0,由此知ε0和ε一定存在，且ε+ε0<λmin(Q).

3结果及其证明

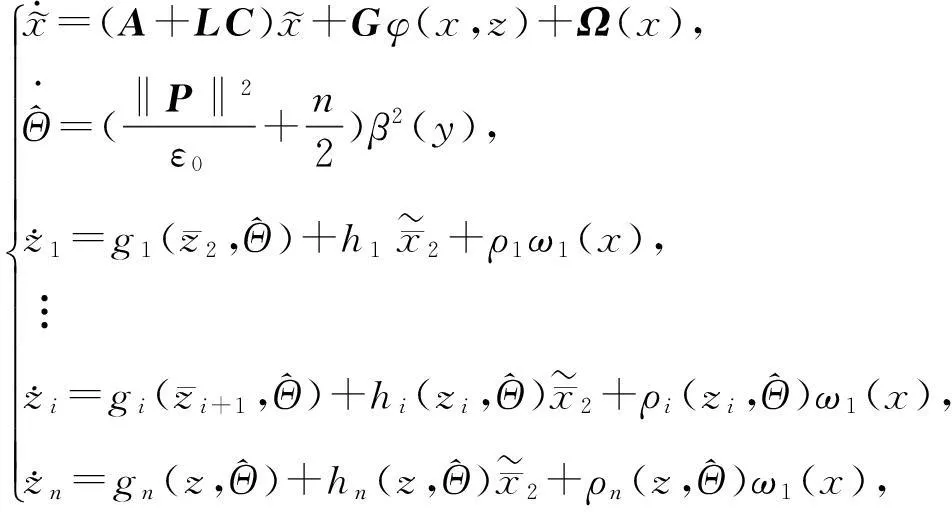
(21)

这里gi,hi,ρi(i=1,2,…,n)充分光滑.

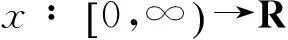
定理1对非线性系统(1),若(H1)—(H3)成立,参数ε0和ε满足不等式(20),则基于观测器(3)所设计的控制器(17)在原点平衡,并实现了系统所有信号渐近收敛或者一致有界.

证明从式(17)可看出控制器u在原点平衡.下面证明闭环系统的稳定性.记c=δ-ε,由式(20)知c>0.再由式(19)得

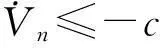
(22)

由此得系统(11)满足:

(23)

进一步,由式(22)知：

(24)

(25)

由此及β(·)的光滑性知β(y)=β(z1)是渐近收敛的.

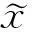
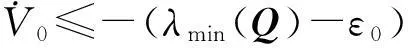
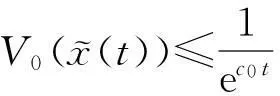
(26)

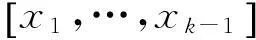
4仿真例子

考虑三阶系统:

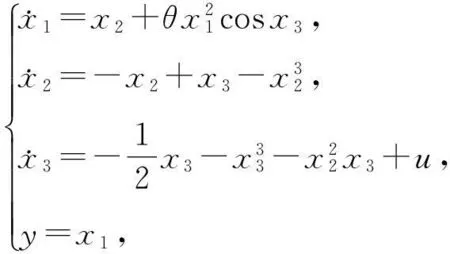
这里设θ=1.此系统可写成系统(2)的形式,并满足假设条件.求解矩阵不等式(4)得:

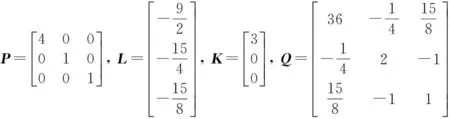
设计观测器:

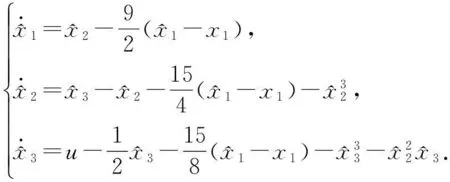
根据上面所给的设计步骤知，控制u为:

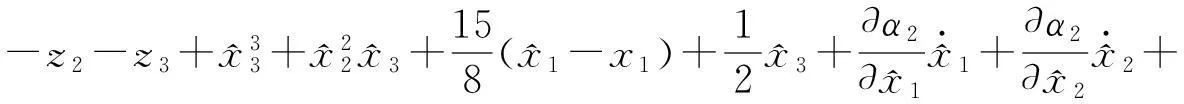
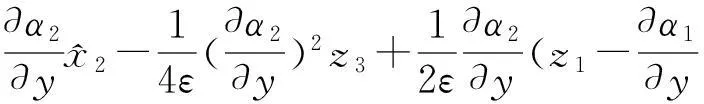
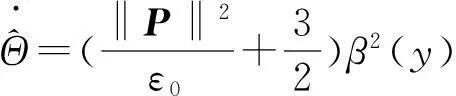
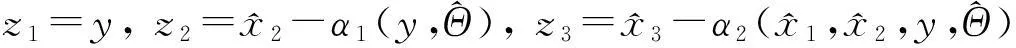
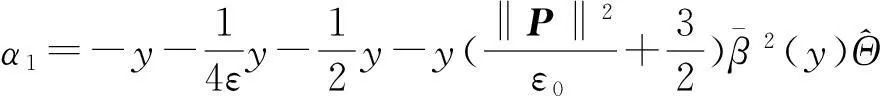
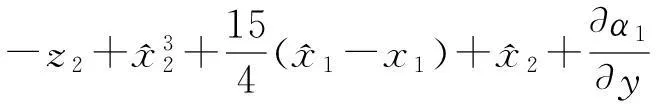
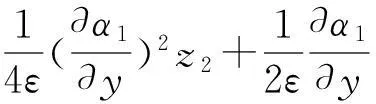
图1　系统状态x 1(实线部分)和观测器状态 1(虚线部分)

图2　系统状态x 2(实线部分)和观测器状态 2(虚线部分)

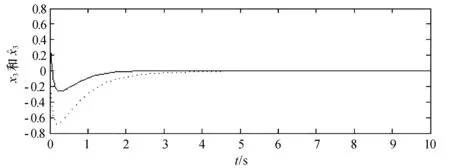
图3　系统状态x 3(实线部分)和观测器状态 3(虚线部分)

图4　系统控制输入u

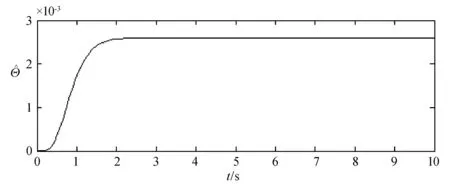
图5　参数Θ的估计值

参考文献：

[1]Krstic M, Kanellakopoulos I, Kokotivic P V. Nonlinear and Adaptive Control Design[M]. New York: Wiley, 1995.

[2]Wang Q D, Jing Y W, Zhang S Y. Robust adaptive ε-output tracking control for a class of uncertain nonlinear systems[J]. Control and Design, 2004,19(6):711-713.

[3]于江波,赵彦,武玉强.一类具有输入状态稳定未建模动态的非线性系统的输出跟踪控制[J].东南大学学报:自然科学版，2011(S1):112-115.

[4]段纳,王璐,赵丛然.一类具有积分输入到状态稳定未建模动态的高阶非线性系统的状态反馈调节[J].控制理论与应用,2011(5):639-644.

[5]Jiang Z P, Praly L. Preliminary results about robust lagrange stability in adaptive non-linear regulation[J].Int J Adaptive Control and Signal Processing, 1992,6(4):285-307.

[6]Jiang Z P, Laurent P. Design of robust adaptive controllers for nonlinear systems with dynamic uncertainties[J]. Automatica, 1998,34(7):825-840.

[7]Murat Areak, Maria Seron, Julio Braslavsky, et al. Robustifieation of Backstepping against input unmodeled dynamics[J]. IEEE Trans Antomat Contr, 2000,45(7):1358-1363.

[8]Wang L Y, Yin G G. Persistent identification of systems with unmodeled dynamies and exogenous disturbanees[J]. IEEE Trans Automat Contr, 2000,45(7):1246-1256.

[9]Sane H S, Sussmann H J, Bernstein D S. Output feedback adaptive stabilization of second-order systems[C]//Proceedings of the American Control Conference, Chicago: American Automatic Control Council, 2000:3138-3142.