电感电流不连续模式Boost变换器多尺度熵分析

电感电流不连续模式Boost变换器多尺度熵分析

徐红梅1，刘嘉琪1，王奥博2

( 1.延边大学工学院 电子信息通信学科， 吉林 延吉 133002；

2.哈尔滨工业大学 电子信息工程系， 黑龙江 哈尔滨 150006 )

摘要：提出一种运用多尺度熵分析开关变换器工作特性的方法.首先给出电感电流不连续模式Boost开关变换器的迭代映射函数；其次通过符号动力学理论得到开关变换器的离散时间序列，并运用熵理论对开关变换器的符号序列进行分析；最后通过对比分析得到电感电流不连续模式Boost开关变换器的混沌特性.

关键词：Boost变换器； 多尺度熵； 混沌特性； 符号动力学

收稿日期：2015-04-22

基金项目：吉林省教育厅科研项目(吉教科合字[2015]第11号);延边大学科技发展项目(延大科合字[2014]第15号);延边大学博士启动基金资助项目(602014093)

文章编号：1004-4353(2015)02-0153-03

中图分类号：TN914.42

Multiscale entropy analysis of the discontinuous inductor current mode Boost switching converter

XU Hongmei1,LIU Jiaqi1,WANG Aobo2

( 1.DepartmentofElectronicandCommunicationEngineering,CollegeofEngineering,YanbianUniversity,

Yanji133002,China; 2.DepartmentofElectronicInformationEngineering,

HarbinInstituteofTechnology,Harbin150006,China)

Abstract：The method that using multiscale entropy to analyze the working characteristic of Boost switching converter is proposed. Firstly, we provide iterative mapping function of the discontinuous inductor current mode Boost switch converter; then the discrete time series of the switch converter is obtained through symbolic dynamic theory, and use entropy theory to analyze the symbolic series of switch converter; finally, we obtain the chaos character of the discontinuous inductor current mode Boost switch converter through contrastive analysis.

Key words： Boost converter; multiscale entropy; chaos character; symbolic dynamic

Boost变换器又称升压变换器，在低电压、便携式电子产器中得到广泛应用.在开关电源设计中，由于Boost变换器的功率开关管一端与电源共地，驱动电路设计更加容易[1]，因此电子工程师们一直在探索Boost变换器拓扑结构变换和提高其工作性能的有效控制方法[2].根据Boost变换器中电感电流的工作方式，可将其分为电感电流连续模式(CCM)和电感电流不连续工作模式(DCM).目前，关于这两种类型变换器的研究已取得了一些成果，例如:文献[3]研究了Boost变换器的能量传输模式和输出纹波电压与电感数值大小的关系；文献[4]对Boost变换器中参数斜坡共振控制能力进行了研究，得出不同共振电压幅值时参数斜坡共振的控制能力及其稳定参数；文献[5]研究了电感电流连续模式下Boost变换器的分数阶建模；文献[6]研究了电压模式控制下不连续传导模式Boost变换器中的切分岔现象.

近年来，随着开关变换器研究方法的深入，信息论中的相关理论已被运用到变换器控制方法的研究中[7].本文提出基于多尺度熵分析Boost变换器工作特性的方法：首先通过建立Boost变换器处于电感电流不连续状态的模型，然后运用符号动力学理论和滑模块方法得到Boost变换器的离散时间序列，并且运用多尺度熵理论分析电感电流不连续模式Boost变换器的混沌动力学特性，从而验证了本文所提出方法的正确性和可行性.

1多尺度熵理论

设一个离散时间序列X={x1，x2，…，xn},将该时间序列进行尺度变换后，得到新序列：

(1)

式中τ为尺度因子，则进行尺度变换后得到的新时间序列的长度为n/τ.当尺度因子τ=1时，新时间序列与原时间序列相同，以下为不同尺度因子时的序列变化：

(2)

2DCM Boost变换器建模

本文利用Tse[8]提出的分析开关变换器的建模方法，对DCM Boost变换器进行多尺度熵分析.根据Boost变换器原理图1，设E为输入电压，X为期望的稳态输出电压，D为稳态占空比，k为反馈比例增益，变换器的工作状态可用如下迭代映射方程近似描述：

土地质量地球化学调查是一项基础性、公益性、战略性的地质调查与研究工作。自2003年至今，山东省地质调查院实施了山东省黄河下游流域生态地球化学调查等4个土地质量地球化学调查项目，完成调查面积16.1万km2(包括部分近岸海域)，使山东省1∶25万土地质量地球化学调查工作全覆盖，调查评价成果显著[1-24]，这些成果已逐步应用于基本农田建设、土地资源保护、整治和开发利用及土壤保护治理和矿产资源勘查等领域。

(3)

其中xn代表第n次迭代电感电流为0时刻的电容电压，其他参数如下：

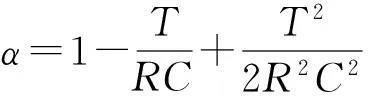
(4)

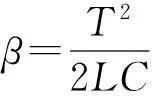
(5)

(6)

d(xn)=D-k(xn-X).

(7)

变换器中的参数值见表1.

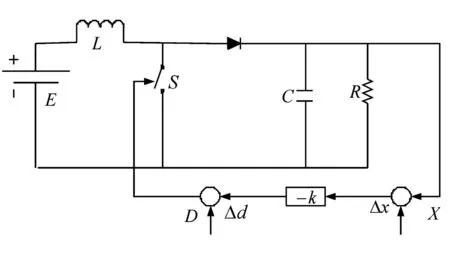
图1　电压反馈型DCM Boost变换器的原理图

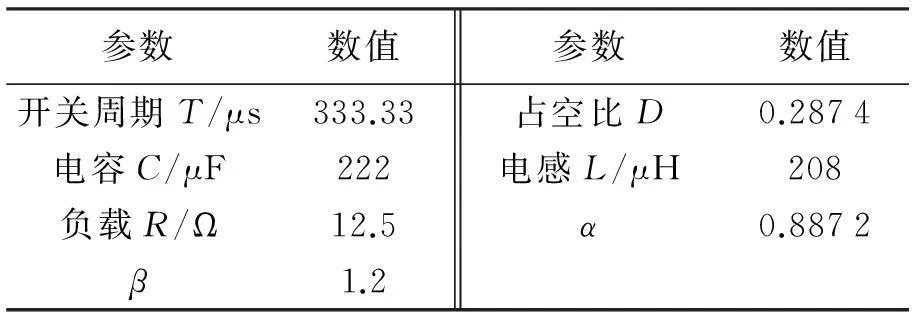
参数数值参数数值开关周期T/μs333.33占空比D0.2874电容C/μF222电感L/μH208负载R/Ω12.5α0.8872β1.2

以反馈比例增益k为变量(取0.01到0.14中的100个数)，初值x0从23.7到29.8取值99次，得到DCM Boost变换器的分岔图，如图2所示.

图2　电压反馈型DCM Boost变换器的分岔图

3DCM Boost变换器的多尺度熵

设原始数据长度L=256，根据式(2)和式(3)，取相同初值，反馈比例增益分别取0.1203和0.1315，通过计算可得到对应的序列及多尺度熵值，如图3所示.从图3可以看出：随着尺度因子的增大，序列的多尺度熵值总体呈现下降趋势，表明序列的复杂度在降低；当初值和尺度因子相同时，不同反馈比例增益对应的多尺度熵值明显不同，而且熵值随着增益的增大而增大，说明当反馈比例增益增大时，序列的数值变化范围增大，进而导致多尺度熵值增大.

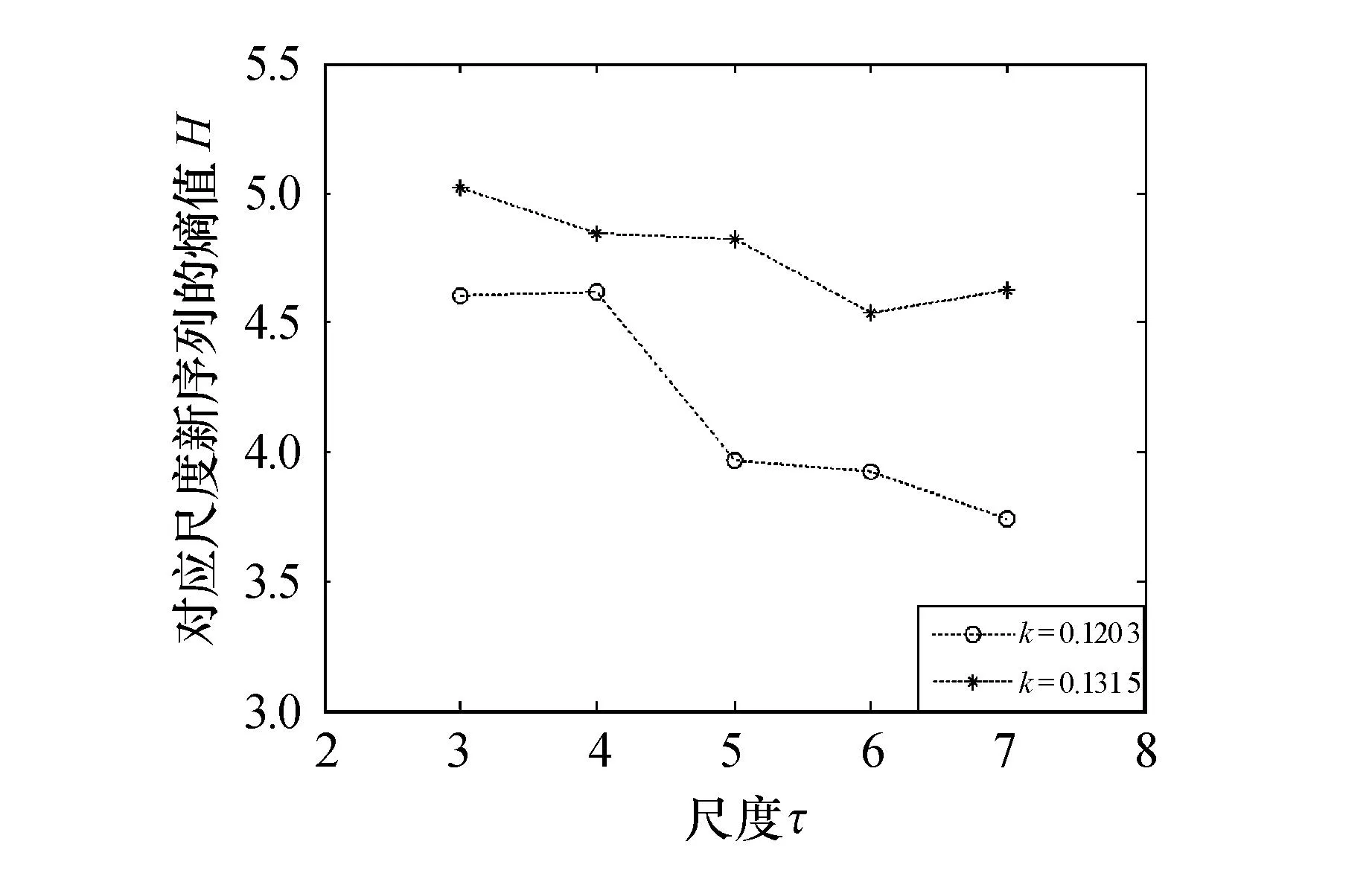
图3　初值x 0=23.7时不同反馈比例增益的多尺度熵

由图2可知，当反馈比例增益k=0.1203时变换器已经处于混沌状态，初值按递增关系取5个随机值，根据式(2)和式(3)计算可得到多尺度熵值，如图4所示.由图4可知：在反馈比例增益相同时，对于同一初值，序列多尺度熵值随着尺度因子的增大总体呈现下降趋势；当初值取最小值时，多尺度熵值的变化范围大，反之，多尺度熵值的变化范围小.多尺度熵值随初值的变化规律与混沌系统的初值敏感性相吻合.

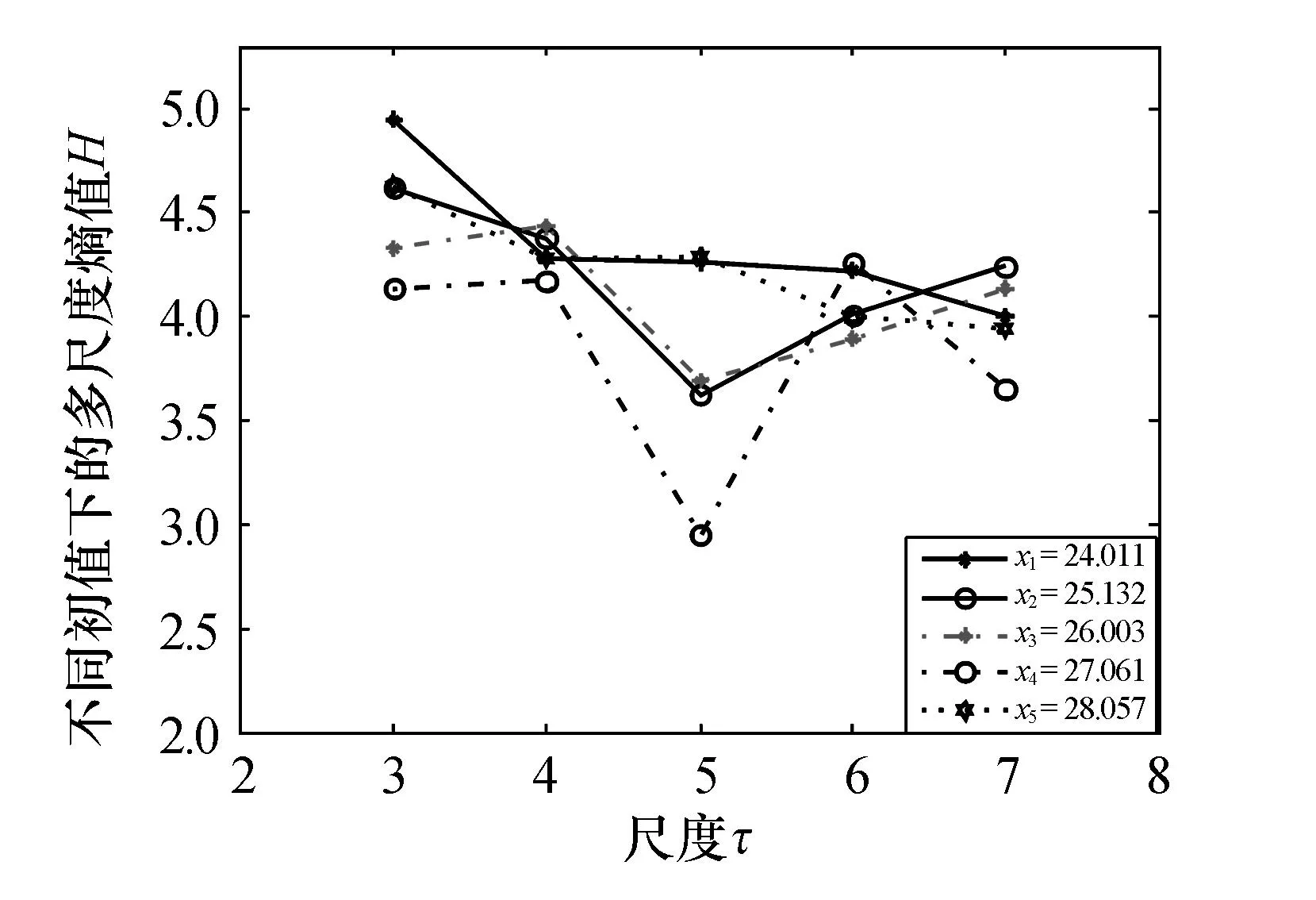
图4　k=0.1203时不同初值对应的多尺度熵

当取反馈比例增益k=0.1315时，开关变换器系统处于各态历经的完全混沌状态，初值取5个随机值，根据式(2)和式(3)计算可得到多尺度熵值，如图5所示.由图5可知，此时的多尺度熵值呈现明显的下降趋势，而且每个初值对应的多尺度熵值的变化范围明显变小.

综合图3—图5可知：DCMBoost变换器处于混沌状态时，不同初值对应不同的多尺度熵值，但是在相同的反馈比例增益下的不同初值所对应的多尺度熵值的变化范围大致相同，而且同一初值在不同反馈比例增益下的多尺度熵值范围不同.根据这一结果，可以将DCMBoost变换器的不同工作状态区分开来，为变接器的利用和控制提供依据.

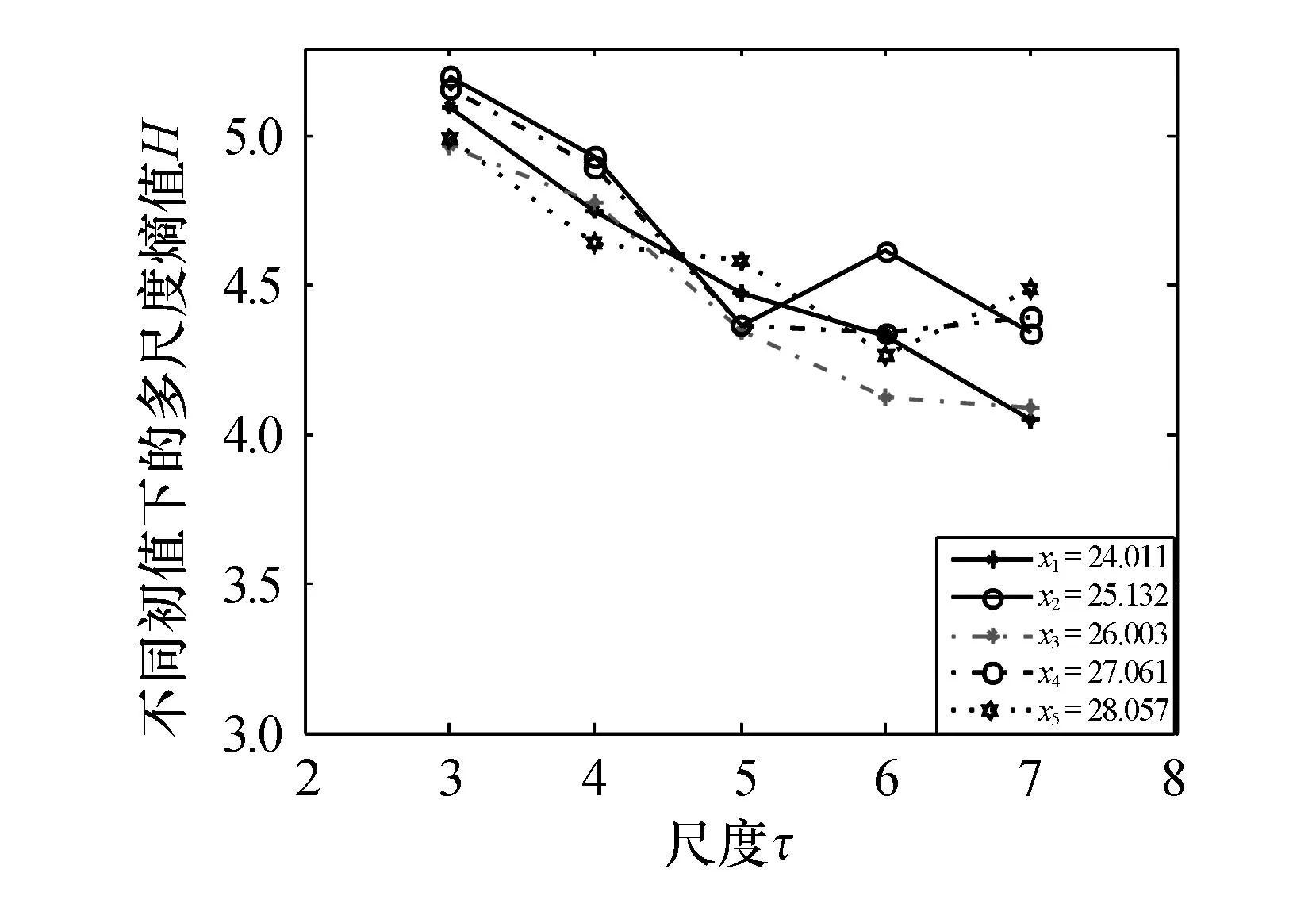
图5　k=0.1315时不同初值对应的多尺度熵

4结束语

本文以电感电流不连续模式的DCM Boost变换器为例，运用多尺度熵理论分析了不同初值、反馈比例增益和变换尺度因子下的多尺度熵值分布规律.分析结果表明：多尺度熵值能够反映DCM Boost变换器的非线性动力学特性，从而证明了本文方法的有效性.将本文结论应用于开关变换器的设计中，将会提高其可靠性和稳定性.

参考文献：

[1]张波,曲颖.电压反馈型Boost变换器DCM的精确离散映射及其分岔和混沌现象[J].电工技术学报,2006,17(3):43-46.

[2]Wang Xuemei, Zhang Bo, Qiu Dongyuan. The quantitative characterization of symbolic series of a Boost converter[J]. IEEE Transactions on Power Electronics, 2011,26(8):2101-2105.

[3]刘树林,刘健,杨银玲,等.Boost变换器的能量传输模式及输出纹波电压分析[J].中国机电学报,2006,26(5):119-124.

[4]程为彬,郭颖娜,康思民,等.Boost变换器中参数斜坡共振控制能力研究[J].物理学报,2009,58(7):4439-4448.

[5]王发强,马西奎.电感电流连续模式下Boost变换器的分数阶建模与仿真分析[J].物理学报,2011,60(7):070506-1-070506-8.

[6]谢玲玲,龚仁喜,卓浩泽,等.电压模式控制不连续传导模式Boost变换器切分岔研究[J].物理学报,2012,61(5):058401-1-058401-7.

[7]程为彬,康思民,汪跃龙,等.功率因数校正Boost变换器中快时标不稳定的形成与参数动态共振[J].物理学报,2011,60(2):020506-1-020506-8.

[8]Tse C K. Flip bifurcation and chaos in three-state Boost switching regulators[J]. IEEE Transactions on Power Electronics, 1994,41(1):16-23.