一类分数阶q-差分方程边值问题正解的存在性

*通信作者： 何延生(1962—)，男，副教授，研究方向为微分方程理论及应用.

一类分数阶q-差分方程边值问题正解的存在性

苏巍,刘畅,李丹,何延生*

( 延边大学理学院 数学系， 吉林 延吉 133002 )

摘要：研究了一类分数阶q-差分方程多点边值问题,其中控制函数含有分数阶导数.首先通过变换将该问题转化为带有分数阶积分控制的边值问题，并分析了格林函数的一些性质；其次利用Arzela-Ascoli不动点定理及上下解方法，证明了该方程正解的存在性；最后通过实例验证了本文所得结论的正确性.

关键词：分数阶q-差分； Bananch空间； 上下解方法； 解的存在性

收稿日期：2015-04-12

文章编号：1004-4353(2015)02-0103-08

中图分类号：O175.6

Existence of positive solutions for a class of the boundary value problems of fractionalq-difference equations

SU Wei,LIU Chang,LI Dan,HE Yansheng*

(DepartmentofMathematics,CollegeofScience,YanbianUniversity,Yanji133002，China)

Abstract：We study a class of the boundary value problems of fractional q-difference equations. Here, the fractional derivative is contained in control function. Firstly, we transform the problem into a boundary value problem with fractional integrals control and analyze some properties of the Green function. Secondly, the existence of the solutions of the equation are proved by using the Arzela-Ascoli fixed point theorem in Banach space and upper and lower solution method. Finally, we give a example to illustrate our results.

Key words： fractional q-differences; Bananch space; upper and lower solution method; existence of solutions

1910年，Jackson[1-2]提出了q-微积分概念,之后由Al-Salam[3]和Agarwal[4]给出了分数阶q-微积分的基本概念和性质.近年来,q-差分微积分在量子模型、信号分析理论等数学物理问题中得到了广泛的研究和应用，其中关于分数阶q-差分方程边值问题解存在性的研究也取得了大量成果[5-14],但这些成果中多数研究的是带有整数阶边值条件的q-差分方程的解，而带有分数阶q-差分边界条件的研究结果相对较少.如：文献[13]的作者研究了带有p-Laplacian算子的三点边值问题

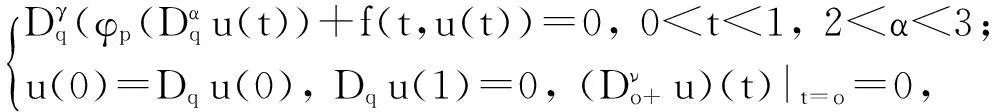
并利用偏序集上的不动点定理证明了正解和非递减解的存在唯一性；文献[14]的作者研究了带有p-Laplacian算子的两点边值问题

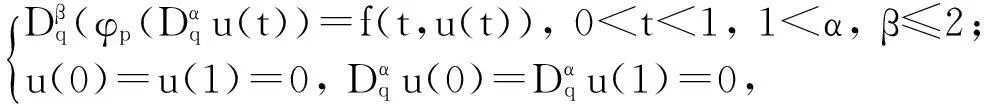
并利用Schauder不动点定理和上下解方法获得了解的存在性结果.

本文研究如下分数阶q-差分方程多点边值问题：

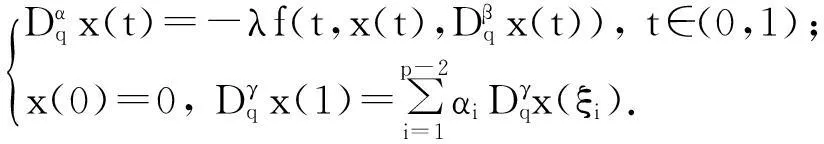
(1)

1预备知识

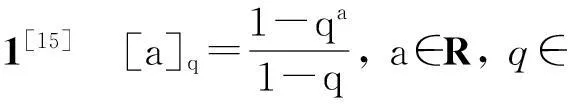
定义2[15]幂指函数(a-b)n的q-类似定义为：

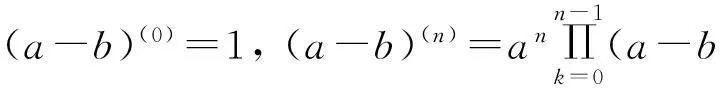
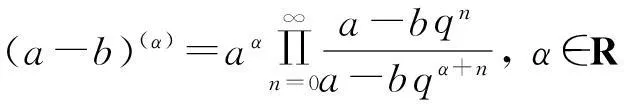
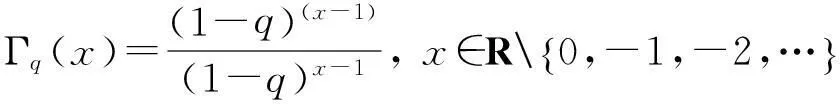
定义4[15]Riemann-Liouville型分数阶q-积分定义为：

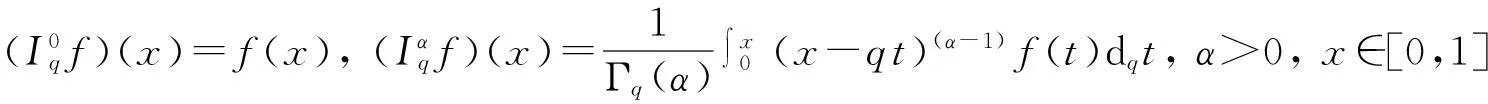
其中f(x)是定义在[0,1]上的函数.

定义5[15]Riemann-Liouville型分数阶q-导数定义为：

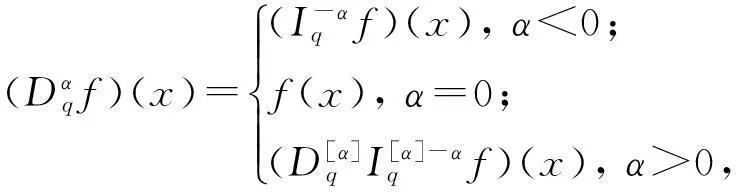
这里[α]是大于或等于α的最小整数.

引理1[15]设α>0,p是正整数，则

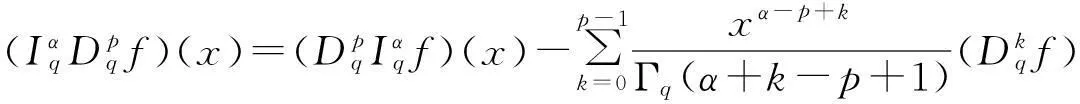
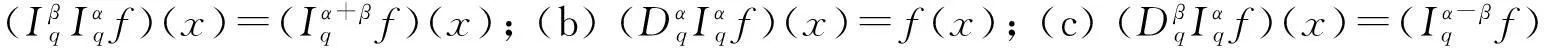
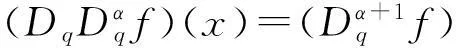
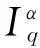
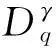
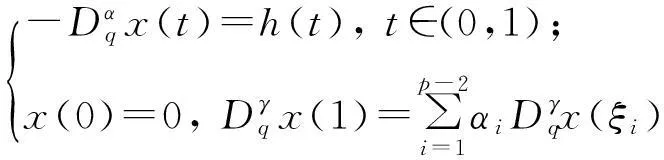
(2)

与边值问题

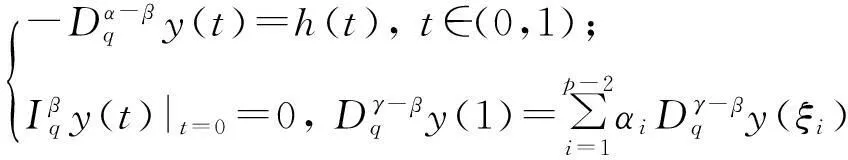
(3)

等价.

类似地有：

引理7边值问题(1)等价于问题:

引理8边值问题(3)等价于问题：

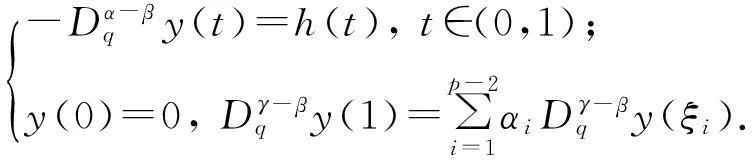
(4)

证明假设y(t)是问题(3)的解,则由引理1和引理4有：

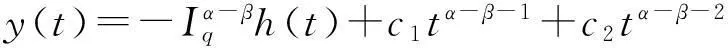
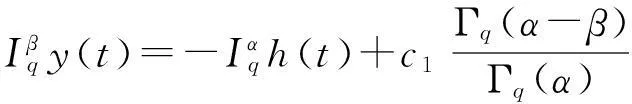
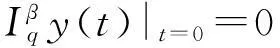
由引理6—8可知，要研究问题(1)的解的存在性，只需研究如下问题解的存在性：

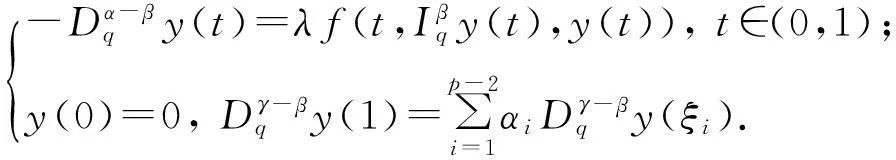
(5)

下面为考虑问题(5)，首先给出上下解的定义如下：

定义6一个连续函数φ(t)称为边值问题(5)的一个下解，若满足

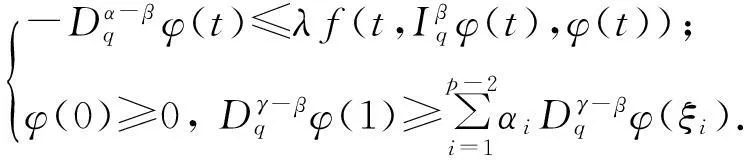
(6)

定义7一个连续函数ψ(t)称为边值问题(5)的一个上解，若满足

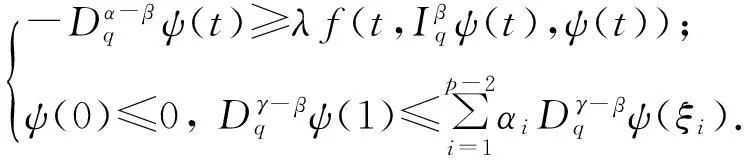
(7)

2Green函数及其性质

为方便,记：

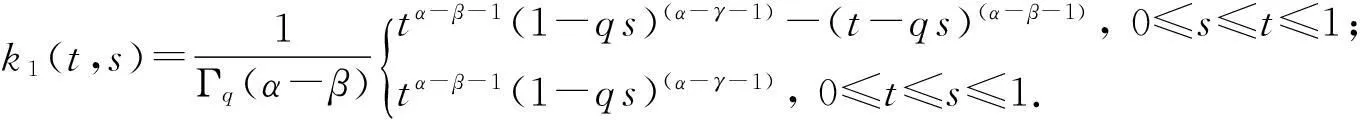
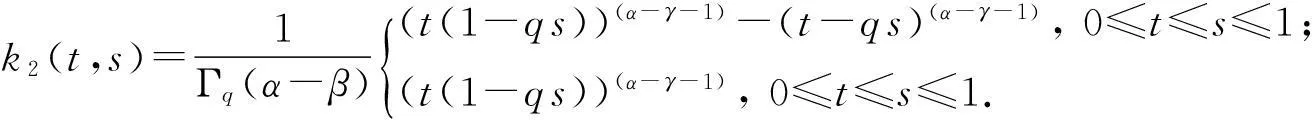
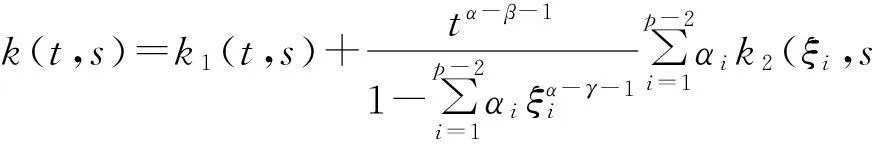
(8)

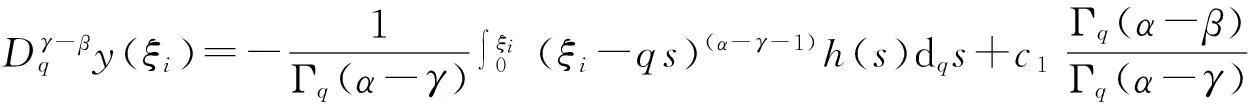
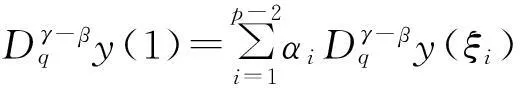
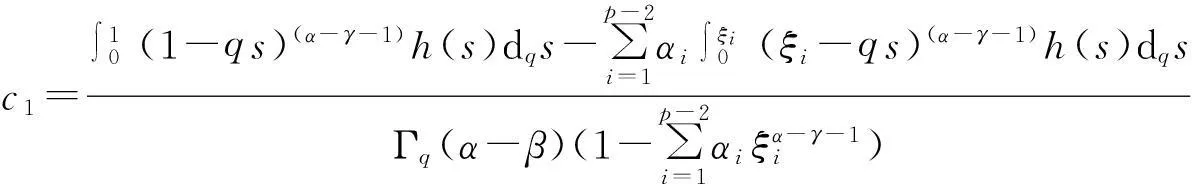
所以问题(5)的唯一解为

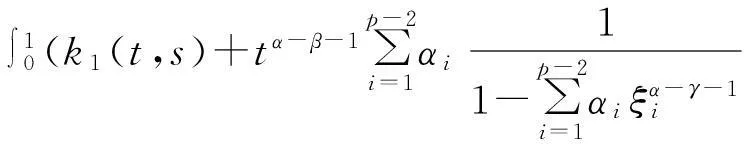
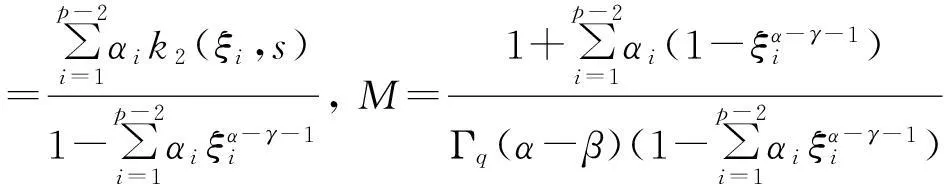
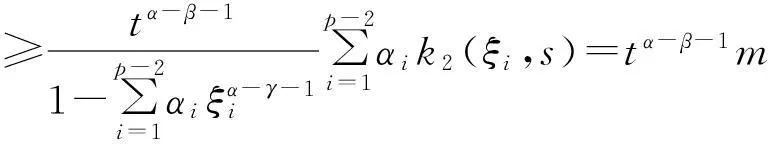
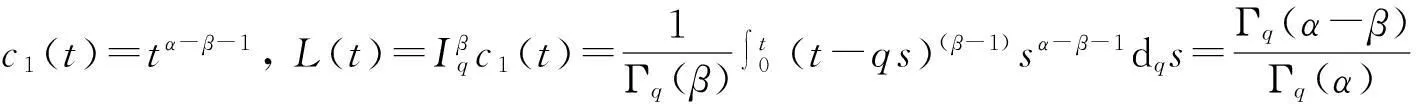
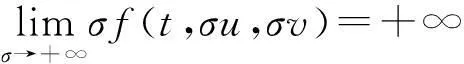
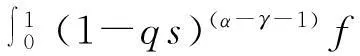
3主要结果及其证明

定理1假设(H1)和(H2)成立，那么存在一个正数λ*，使得对任意的λ∈(λ*,+∞)，问题(5)至少有一个正解y(t)≥L(t),t∈[0,1].

证明假设E=C[0,1]，定义E上的一个锥P及算子Tλ如下：

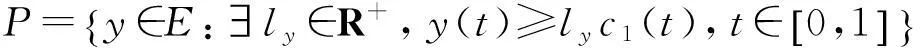
(9)

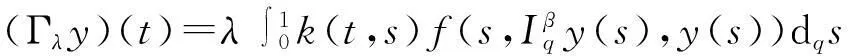
(10)

显然，c1(t)∈P，P是非空的.

下面证明Tλ(P)⊂P.由P的定义知，对任意的ρ(t)∈P，存在一个正数lρ∈P使得ρ(t)≥lρc1(t).由引理10及(H2)得

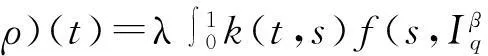
(11)

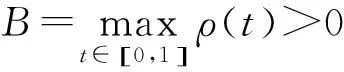
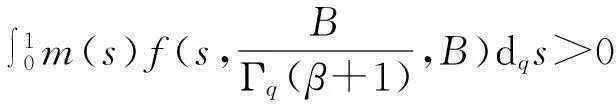
另一方面，

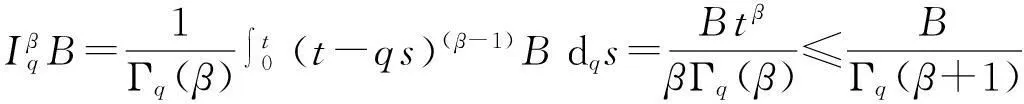
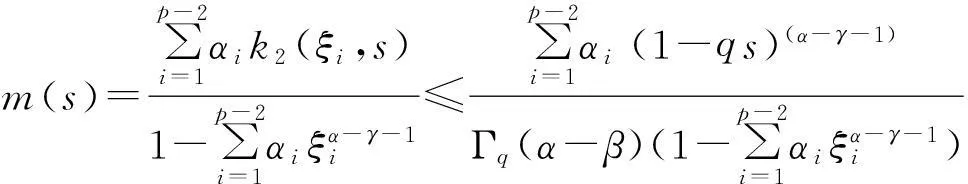
(12)

由式(12)得

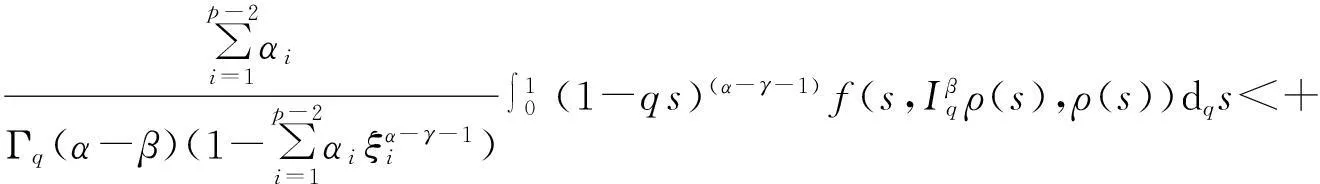
(13)

由引理10及式(11)知

(14)

其中

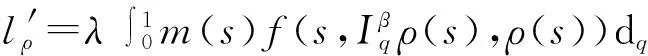
(15)

利用式(11)和式(14)知Γλ(ρ)⊂P.

下面考虑问题(5)的上下解.从(H1)及式(10)知，Γλ关于y是递减的，利用

(16)

且记

(17)

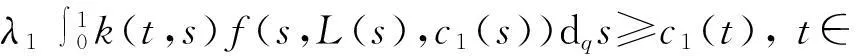
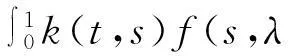
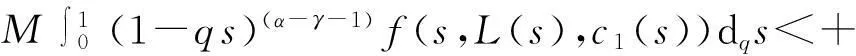
(18)

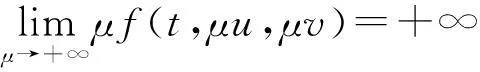
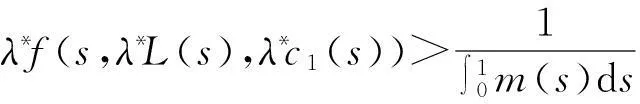
(19)

故由引理10得

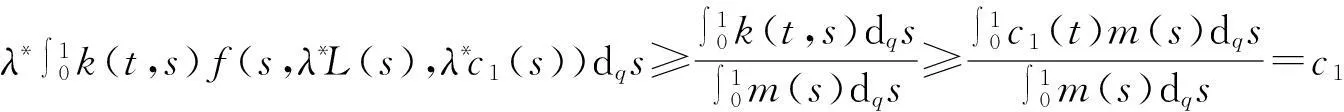
(20)

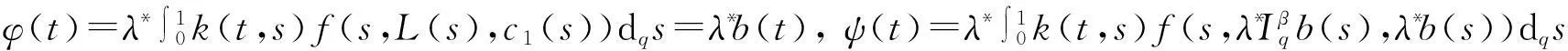
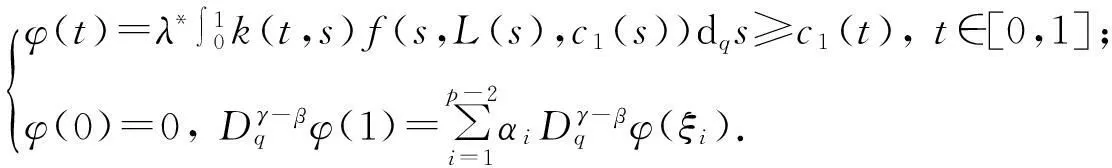
(21)

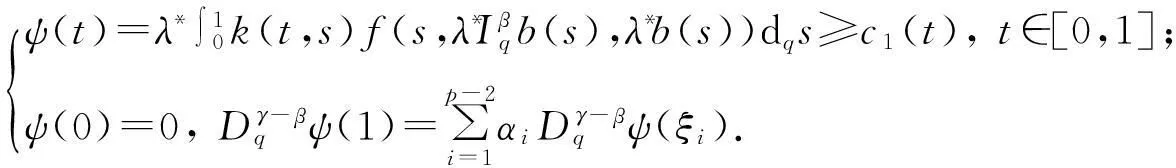
(22)

显然，φ(t),ψ(t)∈P，由式(21)和(22)有

c1(t)≤ψ(t)=(Γλ*φ)(t),c1(t)≤φ(t),t∈[0,1],

(23)

于是

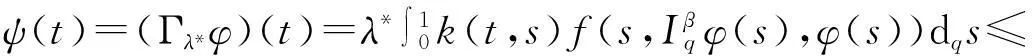
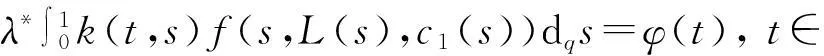
(24)

再由式(23)和(24)得

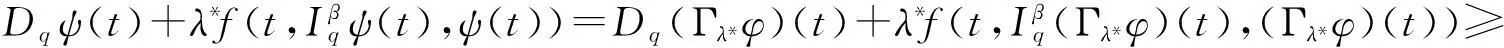
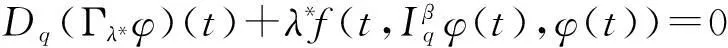
(25)

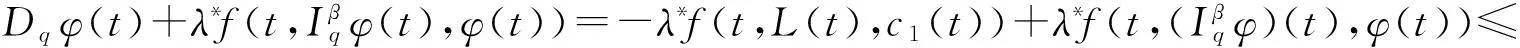
-λ*f(t,L(t),c1(t))+λ*f(t,L(t),c1(t))=0.

(26)

从式(22)及式(24)—(26)可知φ(t),ψ(t)分别是问题(5)的上下解，且φ(t),ψ(t)∈P.

在E中定义如下泛函F及算子Aλ*：

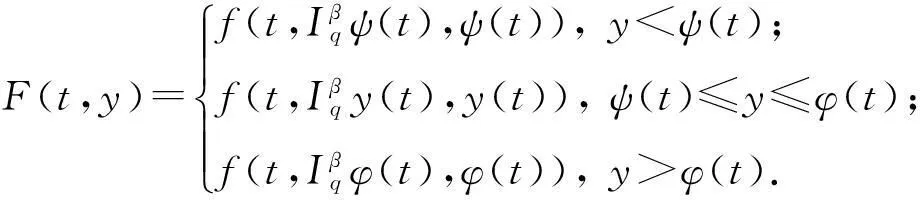
(27)

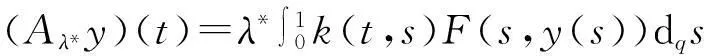
(28)

由(H1)知F∶(0，1)×[0,+∞)→[0,+∞)是连续的.考虑如下边值问题

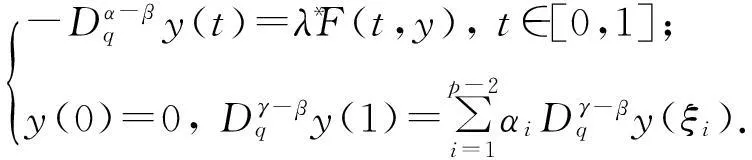
(29)

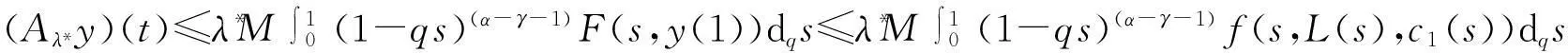
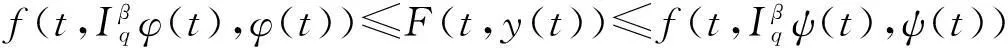
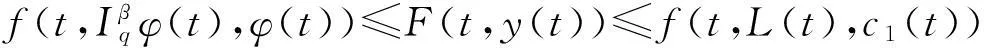
(30)

从式(24)和(26)，有

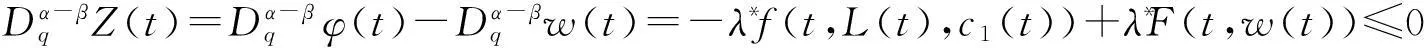
(31)

于是由引理11和式(30)—(31)，有Z(t)≥0，且w(t)≤φ(t).类似地可以推出w(t)≥ψ(t),t∈[0,1],故

ψ(t)≤w(t)≤φ(t),t∈[0,1].

(32)

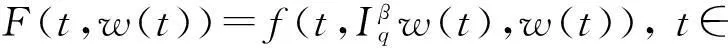
最后由式(32)有w(t)≥ψ(t)≥c1(t),于是

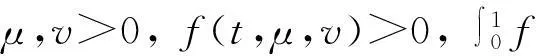
下面考虑f(t,u,v)在u,v=0或t=0,1没有奇异性的情况.给出下列假设条件：

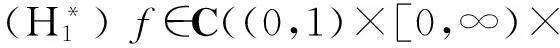
证明在定理1的证明中，用下列的P1来代替P：

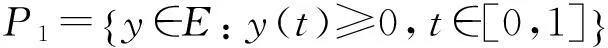
式(24)—(26)由0≤ψ(t)=Γλ0, 0≤φ(t)=(Γλψ)(t)≤ψ(t)代替,由于Γλ0,(Γλψ)(t)∈P，有:

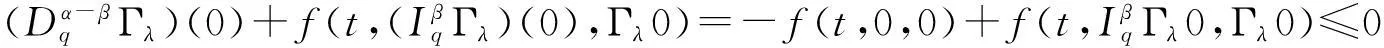
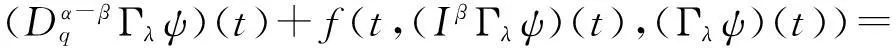
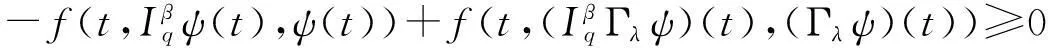
余下的证明类似于定理1，故略去.

推论3假设f(t,u,v)∶[0,1]×[0,∞)×[0,∞)→(0,∞)是连续的且关于u,v递减，则问题(1)至少有一个正解满足x(t)≥L(t),t∈[0,1].

例1考虑边值问题

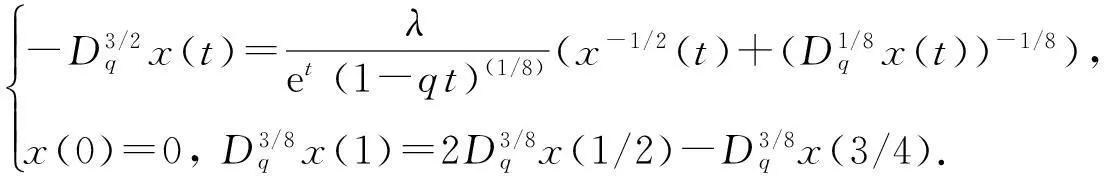
(33)

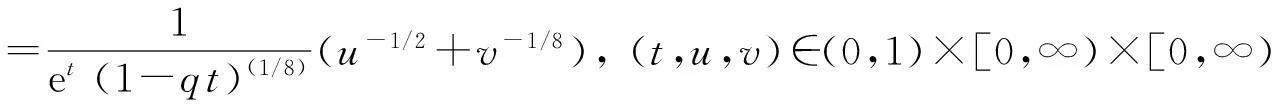
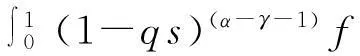
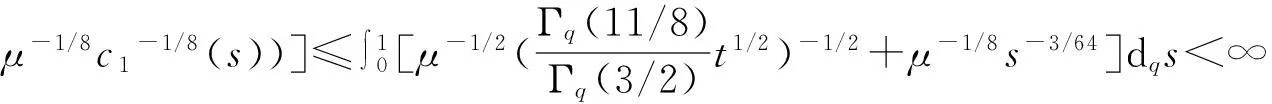
故(H2)成立.据定理1，存在常数λ*>0使得对任意的λ∈(λ*,+∞),问题(33)至少有一个正解满足

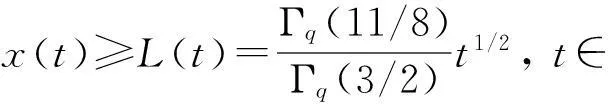
参考文献：

[1]JacksonFH.Onq-definiteintegrals,Quart[J].JPureApplMath, 1910,41:193-203.

[2]JacksonFH.q-differenceequationsAmer[J].JMath, 1910,32(4):305-314.

[3]Al-SalamWA.Somefractionalq-integralsandq-derivatives[J].ProcEdinbMathSoc, 1996,15(2):135-140.

[4]AgarwalRP.Certainfractionalq-integralsandq-derivatives[J].ProcCambridgePhilosSoc, 1996,66:365-370.

[5]EamatyA,YadollahzadehM,DarziR.Existenceofsolutionforanonlocalboundaryvalueproblemwithfractionalq-derivatives[J].JournalofFractionalCalculusandApplications, 2015,6(2):18-27.

[6]AhmadB,NietoJJ,AlsaediA,etal.Existenceofsolutionsfornonlinearfractionalq-differenceintegralequationswithtwofractionalordersandnonlocalfour-pointboundaryconditions[J].JournaloftheFranklinInstitute, 2014,351:2890-2909.

[7]YangWengui.Anti-periodicboundaryvalueproblemsinvolvingnonlinearfractionalq-differenceequations[J].MalayaJournalofMatematik, 2013,4(1):107-114.

[8]El-ShahedM,HassanHA.Positivesolutionsofq-differenceequation[J].ProcAmerMathSoc, 2010,138:1733-1738.

[9]AhmadB,NietoJJ,AlsaediA,etal.Existenceofsolutionsfornonlinearfractionalq-differenceintegralequationswithtwofractionalordersandnonlocalfour-pointboundaryconditions[J].JournaloftheFranklinInstitute, 2014,351:2890-2909.

[10]AnnabyMH，MansourZS.q-FractionalCalculusandEquations[M].BerlinHeidelberg:Springer-Verlag, 2012.

[11]FerreiraR.Positivesolutionsforaclassofboundaryvalueproblemswithfractionalq-differences[J].ComputMathAppl, 2011,61:367-373.

[12]MaD,YangX.Upperandlowersolutionmethodforfourth-orderfour-pointboundaryvalueproblems[J].JComputApplMath, 2009,223(2):543-551.

[13]MiaoF,LiangS.Uniquenessofpositivesolutionsforfractionalq-differenceboundary-valueproblemswithp-Laplacianoperator[J].ElectronJDifferEqu, 2013,174. 2013.

[14]YangW.Positivesolutionforfractionalq-differenceboundaryvalueproblemswithφ-Laplacianoperator[J].BullMalaysMathSoc, 2013,36(4):1195-1203.

[15]PredragMRajkovic,SladanaDMarinkovic,MiomorsStankovic.Fractionalintegralsandderivativesinq-Calculus[J].ApplicableAnalysisandDiscreteMathematics, 2007,1:311-323.