Alzette 的安全性分析*

许 峥， 李永强， 王明生

1. 中国科学院 信息工程研究所 信息安全国家重点实验室， 北京 100093

2. 中国科学院大学 网络空间安全学院， 北京 100049

1 引言

认证加密算法(authenticated-encryption， AE) 是指能同时实现数据加密和真实性认证功能的算法，是密码学家在研究加密算法和认证算法的基础之上， 根据现实应用需求提出的对称密码算法. 随着物联网的发展， 密码算法越来越多地被应用在资源受限的环境中. 由于现有的认证加密算法以及Hash 函数不适用于资源受限的环境中，美国国家标准与技术研究所(NIST)启动了一项进程，以征集、评估并标准化适用于资源受限环境中的带关联数据的认证加密(AEAD) 算法以及Hash 函数[1]. 2019 年4 月18 日， NIST共收到57 个算法， 其中的56 个被接收为第一轮候选算法. 经过公开反馈以及内部评定， NIST 于2019 年8 月30 日公布了32 个第二轮候选算法. 经过更加严格的安全性评估， 2021 年3 月29 日， NIST 公布了10 个决赛候选算法: ASCON、Elephant、GIFT-COFB、Grain-128AEAD、ISAP、PHOTON-Beetle、Romulus、SPARKLE、TinyJambu 以及Xoodyak. 在这10 个决赛候选算法之中， SPARKLE 算法由于使用了新的64 比特S 盒(Alzette) 而备受关注.

Alzette[2]是由Beierle 等人在2020 年美密会上提出的一种ARX (模加、循环移位、异或) 结构的64 比特S 盒. ARX 结构的安全性是通过分析其抗各种攻击的鲁棒性来评估的. 对于ARX 结构最成功的攻击之一是差分类攻击(差分攻击[3]和不可能差分攻击[4，5]). 由于Alzette 是SPARKLE 算法唯一的非线性来源， 而模加又是Alzette 唯一的非线性来源， 因此评估模加的差分性质对评估Alzette 以及SPARKLE 抗差分类分析的安全性是十分关键的.

模加的差分性质已经被研究了几十年. 在2001 年的FSE 会议上， Lipmaa 和Moriai 提出了一种计算具有两个可变输入的模加的差分概率的对数时间算法[6]. 在2010 年的SAC 会议上， Mouha 等人引入了S 函数的概念并利用S 函数来评估具有任意数量输入分支模加的差分概率[7]. 在2020 年的亚密会议上， Azimi 等人提出了一种针对具有一个常量输入的模加的比特向量差分模型[8]. 为了更好地评估分组密码抗差分分析的安全性， Lai 等人在1991 年的欧密会议上提出了Markov 密码的概念[9]. 在Markov 假设下， 一条差分路径的概率可以通过将每一轮的差分传播的概率相乘得到. 事实上， Markov 假设被用于几乎所有对分组密码的差分攻击以及不可能差分攻击中. 在近二十年中， 利用自动化工具搜索差分路径以及不可能差分区分器成为了一种新的趋势. 这些自动化工具主要分为三类: 利用Matsui 算法类的分支定界搜索算法[10-13]、利用混合整数线性规划(MILP) 模型[14，15]以及利用SAT/SMT 求解器[16-21]. 这些方法都是基于Markov 假设的. 在Markov 假设下， ARX 结构的差分路径的概率等于每一轮中的每个模加的差分概率的乘积. 然而， 由于Alzette 中没有任何的密钥注入， 利用基于Markov 假设的自动化搜索方法来搜索Alzette 的差分路径以及不可能差分区分器， 可能会将无效的差分路径识别为有效并遗漏一些有效的不可能差分区分器， 从而导致对Alzette 抗差分类分析的安全性评估不够准确. 因此， 提出一种能够更好地过滤无效的差分路径的方法是十分重要的.

为了更好地过滤无效差分路径， 密码学家研究了差分比特之间的关系并部分解决了上述问题. 在2005年的欧密会议和美密会议上， Wang 等人利用符号差分发现了MD4、MD5 和SHA-1 的碰撞[22-24]. 随后， Leurent 对于连续的异或差分比特提出了多比特限制的概念并提出了一种搜索有效差分路径的自动化工具: ARX Toolkit. 利用该工具， Leurent[25]发现了Yu 等人[26]只利用符号差分找到的一条Skein 算法的差分路径是无效的. 在2013 年， Mouha 等人[20]利用Lipmaa-Moriai 限制条件以及符号差分搜索3轮Salsa20 的最优差分路径. 他们发现了一条ARX Toolkit 无法过滤的差分路径， 证明Leurent 的自动化工具只能捕捉到连续比特之间的关系而无法捕捉非连续比特之间的关系， 因此该工具依然无法成功过滤部分无效的差分路径. 然而， Mouha 等人的方法是自动化与手动推导相结合的方法， 无法完全自动化地过滤无效的差分路径， 因此不适用于搜索不可能差分区分器.

本文研究了Alzette 抗差分类分析的安全性. 对于模加操作上的有效异或差分， 通过利用符号差分的概念， 本文给出了符号差分比特之间关系的比特向量表示. 通过将Lipmaa-Moriai 限制条件以及符号差分比特约束条件转化为可满足性模理论(satisfiability modulo theories， SMT) 问题， 本文提出了一种基于SAT/SMT 求解器的ARX 结构不可能差分区分器自动化搜索工具. 该自动化工具是首个利用Lipmaa-Moriai 限制条件以及符号差分搜索ARX 结构不可能差分区分器的自动化工具. 通过利用符号差分， 该自动化工具可以捕捉连续比特以及非连续比特之间的关系; 通过利用Lipmaa-Moriai 限制条件，该自动化工具可以有效地过滤仅满足符号差分比特约束条件而不满足Lipmaa-Moriai 限制条件的无效差分路径. 因此， 利用该自动化工具可以发现被传统搜索方法忽略的有效的不可能差分区分器. 将本文提出的自动化工具用于搜索具有常数c= 0xb7e15162 的Alzette (即A0xb7e15162) 的不可能差分区分器: 在输入差分汉明重量为1、输出差分汉明重量为1 的条件下， 我们发现了4096 个不可能差分区分器; 在输入差分汉明重量为2、输出差分汉明重量为1 的条件下， 我们发现了128 993 个不可能差分区分器. 然而，在输入差分汉明重量为2、输出差分汉明重量为1 的条件下， 利用传统方法搜索Alzette 的不可能差分区分器， 我们发现了128 767 个不可能差分区分器， 证明本文提出的自动化工具能够更好地过滤无效差分路径. 因此， 利用本文提出的方法， 密码分析者可以更好地评估ARX 结构抗不可能差分分析的安全性， 从而给出ARX 结构更加精确的安全性评估结果. 同时， 由于Alzette 是一个SPECK 类结构， 我们分别利用本文提出的自动化搜索工具以及传统方法搜索4 轮无密钥注入SPECK64[27]的不可能差分区分器. 在输入差分汉明重量为2、输出差分汉明重量为1 的条件下， 我们分别发现了128 976 个以及128 018 个不可能差分区分器.A0xb7e15162与4 轮无密钥注入SPECK64 的不可能差分区分器的数量如表1 所示. 据我们所知， 这是首次利用不可能差分性质评估Alzette 的安全性.

表1 一步A0xb7e15162 与4 轮无密钥注入SPECK64 不可能差分区分器的数量Table 1 Numbers of impossible differential characteristics for A0xb7e15162 and 4-round no-key SPECK64

本文结构安排如下: 第2 节简要介绍本文中所用到的符号、Lipmaa-Moriai 限制条件、符号差分、Alzette 的结构以及SPECK 算法等预备知识; 第3 节介绍如何利用Lipmaa-Moriai 限制条件以及符号差分比特约束条件， 构建基于SAT/SMT 求解器的ARX 结构不可能差分区分器自动化搜索工具; 第4 节将新的自动化工具以及传统的搜索方法应用于搜索Alzette 和4 轮SPECK64 的不可能差分区分器;第5 节总结本文工作.

2 符号、预备知识及算法简介

2.1 符号

本文中使用的符号如下所示:

2.2 预备知识

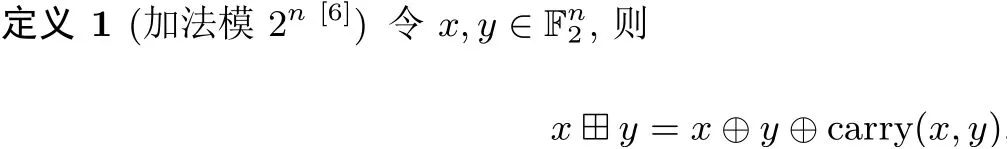
其中mask(n-1) 表示0‖1n-1. 在下文中， 称公式(1) 和公式(2) 为Lipmaa-Moriai 限制条件.

定义3 (符号差分[22-24]) 符号差分Δ±x可以将异或差分分为三种情况:

2.3 Alzette 简介

在2020 年美密会议上， Beierle 等人[2]提出了一种名为Alzette 的64 比特基于ARX 的S 盒. 它是一种具有两个分支的4 轮SPECK 类结构， 并且由一个任意的常数c ∈F322来参数化. Alzette 的描述如算法1、图1 所示.

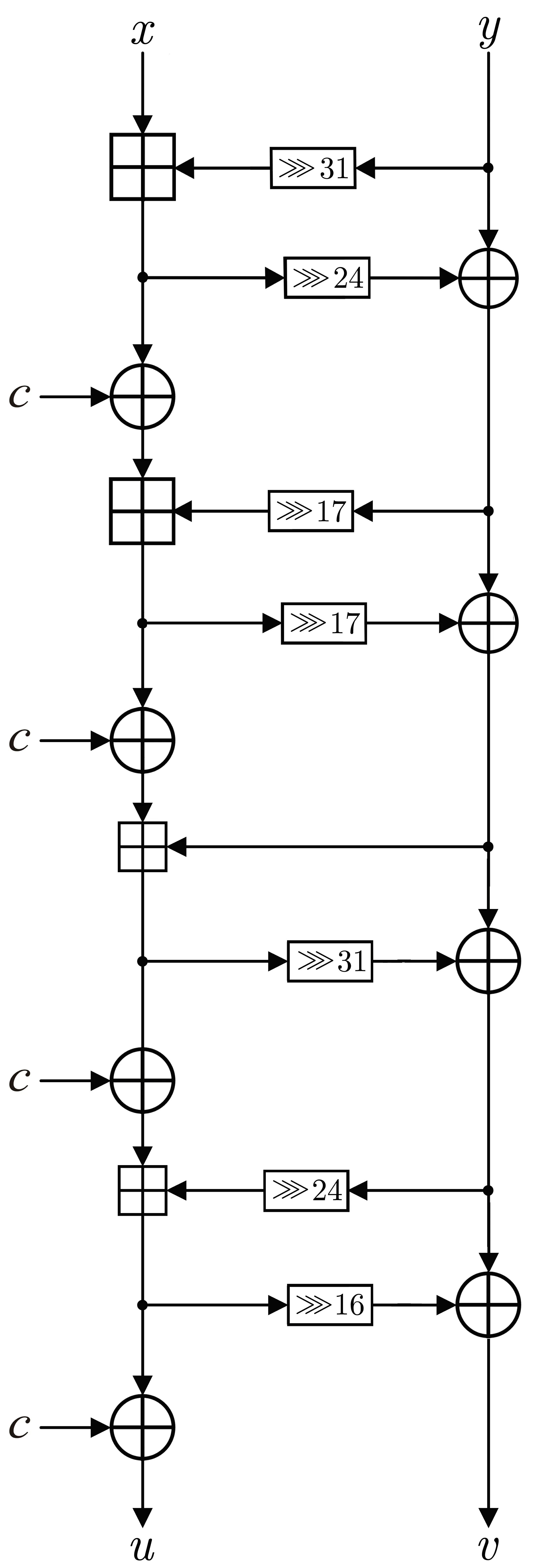
图1 Alzette 实例AcFigure 1 Alzette instance Ac

算法1 Alzette 实例Ac Input: (x，y) ∈F32 2 ×F322 Output: (u，v) ∈F322 ×F322 1 x ←x ⊞(y ≫31);2 y ←y ⊕(x ≫24);3 x ←x ⊕c;4 x ←x ⊞(y ≫17);5 y ←y ⊕(x ≫17);6 x ←x ⊕c;7 x ←x ⊞(y ≫0);8 y ←y ⊕(x ≫31);9 x ←x ⊕c;10 x ←x ⊞(y ≫24);11 v ←y ⊕(x ≫16);12 u ←x ⊕c;13 return (u，v);

2.4 SPECK 简介

美国国家安全局(NSA) 于2013 年发布了SPECK 族轻量分组密码算法[27]. 根据算法的分组长度(32、48、64、96 以及128 比特)，共包括5 类分组密码算法: SPECK32、SPECK48、SPECK64、SPECK96以及SPECK128. 通常， SPECK2n/mn表示具有2n比特分组长度以及mn比特密钥长度的SPECK 算法， 其中n ∈{16，24，32，48，64}、m ∈{2，3，4}且依赖于n的取值. 令(Li-1，Ri-1) 表示第i轮的输入，则第i轮的输出如下计算:

其中Ki表示轮密钥. 当分组长度是32 比特时， (α，β) = (7，2)， 否则(α，β) = (8，3). SPECK 的轮函数如图2 所示.

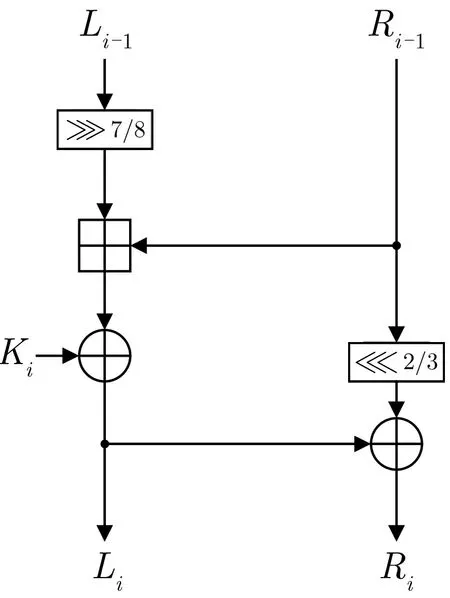
图2 SPECK 轮函数Figure 2 Round function of SPECK

3 基于SAT/SMT 求解器的ARX 结构不可能差分区分器自动化搜索工具

在本节中， 我们提出了一种新的基于SAT/SMT 求解器的ARX 结构不可能差分区分器自动化搜索工具. 由于该自动化工具不仅包含了传统搜索方法所包含的约束条件(Lipmaa-Moriai 限制条件)， 还包含了传统搜索方法未包含的约束条件(符号差分比特约束条件)， 因此， 该自动化工具能够更好地过滤无效的差分路径， 并找到被传统搜索方法所遗漏的有效的不可能差分区分器。

3.1 构建基于SAT/SMT 求解器的ARX 结构不可能差分区分器自动化搜索工具

在文献[20] 中， Mouha 等人利用SAT/SMT 求解器自动化搜索3 轮Salsa20 的最优差分路径. 尽管他们发现了一些差分路径是无效的， 但他们的搜索模型中仅包含了Lipmaa-Moriai 限制条件以及异或差分的传播， 这意味着他们的模型无法自动地过滤那些满足Lipmaa-Moriai 限制条件以及异或差分传播的无效差分路径.

为了自动地过滤这些特殊的差分路径， 本文提出的自动化搜索工具不仅包含了传统搜索方法所包含的约束条件， 还包含了符号差分的传播以在异或差分传播中添加值传播的信息.

本文将搜索不可能差分区分器的问题转化为布尔可满足性问题(Boolean satisfiability problem，SAT)， 然后利用SAT 求解器进行求解. 然而， ARX 结构所包含的都是n比特向量上的操作， 但是SAT问题仅能包含布尔变量以及与(AND)、或(OR)、非(NOT) 操作. 由于SMT 问题支持比特向量变量以及比特向量操作， 且SMT 问题是SAT 问题的推广， 因此本文使用SMT 问题来代替SAT 问题. 一旦一个SMT 问题被建立， SMT 求解器可将SMT 问题转化为SAT 问题， 并利用SAT 求解器进行求解. STP求解器[28]是一个典型的SMT 求解器， 我们利用STP 求解器求解本文中所有的SMT 问题.

对于一个变量分支与一个常数的异或操作的符号差分传播， 由于输出符号差分的取值依赖于常数， 本文用定理1 处理这种情况.

定理1 令x，x′，y，y′，z，z′∈Fn2. 对于z=x ⊕C以及z′=x′⊕C， 假设C是常数， 则有Δz=Δx以及如下符号差分比特之间的关系:

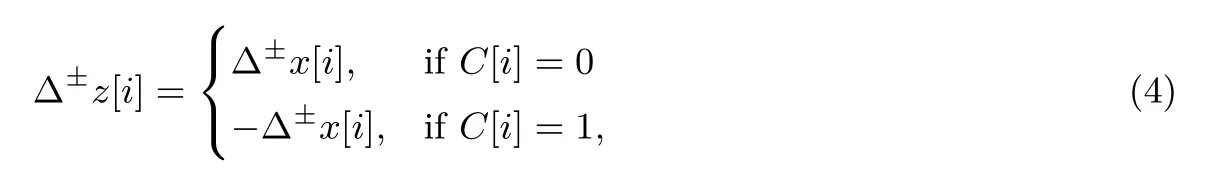
其中， 0≤i ≤n-1.

我们可以用公式(4) 来描述一个变量分支与一个常数的异或操作的符号差分传播.

使用上述方法， 可以构建一个描述Lipmaa-Moriai 限制条件、异或差分传播以及符号差分传播的SAT/SMT 求解模型. 如果对ARX 结构的输入差分(InD) 以及输出差分(OutD) 进行赋值， 则可以得到指定输入差分到指定输出差分是否是一个可能的映射， 即: InD ↮OutD 或者InD↔OutD. 通过在本文提出的搜索模型中添加以下两条命令， 即可完成该映射的可能性判断:

当STP 返回Valid 时， 则InD ↮OutD， 即找到一个不可能差分区分器; 当STP 返回一条差分路径时， 则InD↔OutD， 且该差分路径是有效的.

至此， 我们可以通过以上完整的架构来构建用于搜索ARX 结构不可能差分区分器的自动化工具. 该自动化工具可以有效地过滤不符合Lipmaa-Moriai 限制条件以及符号差分比特约束条件的无效差分路径.

4 自动化搜索Alzette 和无密钥注入的SPECK64 不可能差分区分器

在本节中， 我们将第3 节中提出的自动化工具用于搜索Alzette 和无密钥注入的SPECK64 不可能差分区分器， 并找到了被传统搜索方法忽略的不可能差分区分器.

在文献[2] 中， Alzette 的设计者宣称， Alzette 的设计安全性指标之一是两步Alzette (即8 轮) 的差分界与线性界要强于8 轮SPECK64. 在Alzette 以及SPARKLE 的设计文档中， 设计者仅通过搜索不同步数Alzette 的最优(或次优) 差分路径来评估其抗差分分析的安全性. 除了上述设计文档外， 唯一对Alzette 的安全性分析结果发表在2021 年欧密会议上[29]. 然而， 文献[29] 中的安全性分析是关于差分-线性密码分析的. 到目前为止， 还没有任何对Alzette 不可能差分区分器的公开分析结果. 由于Alzette 是一个S 盒， 因此最直接的分析其抗差分类分析安全性的方法是计算它的差分分布表(difference distribution table， DDT). 然而， 由于Alzette 是操作在64 比特上的S 盒， 计算其DDT 是无法实现的. 因此， 需通过间接的方法评估其差分的分布情况. 对于任意操作在n比特上的S 盒， 对于任意给定的输入差分， 有如下性质:

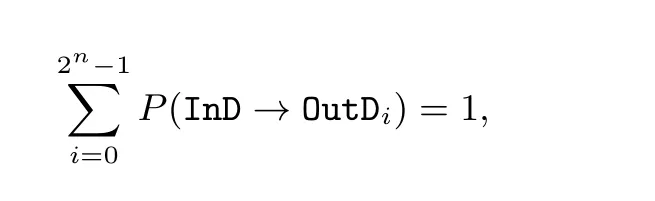
其中OutDi表示OutD =i. 因此， 若一个S 盒的DDT 中为0 的项越少， 该S 盒的差分呈现较为均匀分布的概率越高， 则该S 盒能够较好抗差分类分析的概率越高. 由此可见， 搜索Alzette 的不可能差分区分器对评估Alzette 抗差分类分析的安全性是十分有意义的.

由于Alzette 没有密钥注入， 为了更好地对比Alzette 与SPECK64 的安全性， 本文搜索无密钥注入的SPECK64 不可能差分区分器. 其次， 由于每一步Alzette 使用不同的常数进行实例化， 而无论几轮的无密钥注入SPECK64 都相当于使用全0 密钥进行实例化， 因此搜索一步Alzette 与4 轮SPECK64 的不可能差分区分器能够更好地对比Alzette 与SPECK64 的安全性.

4.1 自动化搜索Alzette 不可能差分区分器

在搜索一步Alzette 不可能差分区分器时， 本文选择常数c= 0xb7e15162 (SPARKLE 使用的8 个常数之一) 来实例化Alzette.

(1) 在wt(InD) = 1 且wt(OutD) = 1 的限制条件下， 利用本文提出的自动化工具， 我们找到了4096个不可能差分区分器; 利用传统搜索方法， 我们同样找到了4096 个不可能差分区分器.

(2) 在wt(InD) = 2 且wt(OutD) = 1 的限制条件下， 利用本文提出的自动化工具， 我们找到了128 993 个不可能差分区分器; 利用传统搜索方法， 我们仅找到128 767 个不可能差分区分器.

上述结果说明， 利用仅包含Lipmaa-Moriai 限制条件以及异或差分传播的传统方法搜索ARX 结构不可能差分区分器， 可能会遗漏一些有效的不可能差分区分器; 然而， 利用本文提出的自动化工具， 我们可以搜索到这些区分器.

4.2 自动化搜索无密钥注入SPECK64 不可能差分区分器

为了更好地对比Alzette 与SPECK64 的安全性， 本文搜索4 轮无密钥注入SPECK64 的不可能差分区分器.

在wt(InD)=2 且wt(OutD)=1 的限制条件下， 利用本文提出的自动化工具， 我们找到了128 976 个不可能差分区分器; 利用传统搜索方法， 我们仅找到128 018 个不可能差分区分器.

我们发现， 无论利用本文提出的自动化工具还是利用传统方法， 一步Alzette 不可能差分区分器的数量都多于4 轮无密钥注入SPECK64 不可能差分区分器的数量. 因此， 如果从搜索不可能差分区分器的角度来评估ARX 结构的差分分布， Alzette 抗差分分析的安全性可能弱于SPECK64， 这与Alzette 设计者的结论相反. 尽管Alzette 的设计者利用两步Alzette 最优差分路径的概率小于8 轮SPECK64 来证明Alzette 抗差分分析的安全性强于SPECK64， 但是由于Alzette 是一个S 盒， 因此， 只能通过差分的概率而不是差分路径的概率来评估其安全性. 然而， Alzette 与SPECK64 的差分概率之间的大小关系无法由最优差分路径概率之间的大小关系导出. 因此， Alzette 设计团队的安全性评估是不够全面的. 据我们所知， 这是首次利用不可能差分性质评估Alzette 的安全性.

5 结论

本文研究了Alzette 抗差分类分析的安全性. 对于模加操作上的有效异或差分， 通过利用符号差分的概念， 本文给出了符号差分比特之间关系的比特向量表示. 通过将Lipmaa-Moriai 限制条件以及符号差分比特约束条件转化为SMT 问题， 本文提出了一种基于SAT/SMT 求解器的ARX 结构不可能差分区分器自动化搜索工具. 该自动化工具是首个利用Lipmaa-Moriai 限制条件以及符号差分搜索ARX 结构不可能差分区分器的自动化工具. 利用该工具可以发现被传统搜索方法忽略的有效的不可能差分区分器. 利用上述自动化工具以及传统方法搜索Alzette 的不可能差分区分器， 我们发现， 该自动化工具能够发现更多的不可能差分区分器， 证明该自动化工具能够更好地过滤无效差分路径. 此外， 将该自动化搜索工具用于搜索4 轮无密钥注入SPECK64 不可能差分区分器， 我们发现4 轮无密钥注入SPECK64 不可能差分区分器的数量少于Alzette 不可能差分区分器的数量， 说明Alzette设计团队的安全性评估是不够全面的. 据我们所知， 这是首次利用不可能差分性质评估Alzette 的安全性. 我们希望本文提出的方法有助于评估ARX 结构抗差分类分析的安全性并有助于ARX 密码的设计.