序列型分数阶差分方程解的存在唯一性
2021-02-14李小敏惠小健
李小敏, 惠小健
(西京学院理学院, 西安 710123)
虽然分数阶与整数阶导数的概念几乎是同一时期出现的, 但是由于其复杂性及缺乏工程背景使得近三百年内分数阶微积分发展较为缓慢.随着计算机技术的迅猛发展及自然界中诸多分数维背景现象的显现,使得分数阶微积分理论引起了国内外学者的广泛关注[1-5],对分数阶差分方程的研究逐渐兴起,相关的理论也在不断完善[6-8],研究已取得了一些成果[9-10].相对于整数阶系统,分数阶系统能够更加真实地描述自然界中的某些现象, 尤其是对于具有记忆和遗传性的系统,使得分数阶系统在物理学、控制工程及生物工程等领域有非常广泛的应用[11-13].分数阶系统的研究是以分数阶微分及差分方程为理论基础,而差分方程解的重要性是不容被忽视的.大多数情况下,分数阶差分方程的解析解不易求得; 因此,研究解的存在唯一性理论显得尤为重要.近年来,许多学者对整数阶、分数阶差分方程解的存在性问题进行了研究,并取得了较好的研究成果,但对于序列型分数阶差分方程的研究较少.序列型分数阶差分的意义在于,可将差分算子Δσn的阶次σn(σn>1)分解成若干个阶次为αi(0≤αi≤1,i=1,2,…,n)的差分算子,无论是在Riemann-Liouville定义下还是Caputo定义下研究差分方程的理论性质,阶次介于0到1都比阶次大于1的差分方程简便得多.程金发[14]系统地提出了分数阶和分、差分的定义及分数阶差分方程的定义, 并证明了基于向后差分的Riemann-Liouville型分数阶差分方程、Caputo型分数阶差分方程及序列型分数阶差分方程解的存在唯一性.本文基于文献[14]给出的向后差分的定义,推导出基于向前分数阶差分的Z变换公式,并通过Z变换及离散Mittag-Leffler函数的性质, 证明基于向前差分的序列型分数阶线性及非线性差分方程解的存在唯一性.
1 分数阶差分与和序列型差分
1.1 向前差分与和分
定义1[14]设n∈N+,称x(n)=x(n)-x(n-1)为x(n)一阶向后差分, Δx(n)=x(n+1)-x(n)为x(n)一阶向前差分.定义Δkx(n)=ΔΔ(k-1)x(n)为x(n)的k阶向前差分, 其中k∈N+.
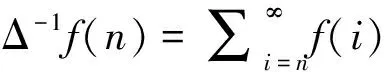
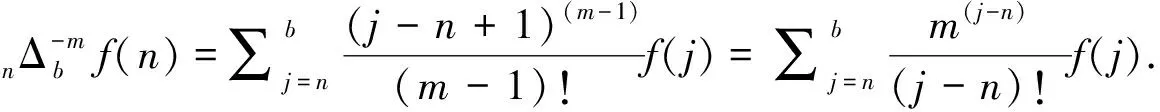
性质1当k1∈N+,k2∈Z时, 有Δk1Δk2x(n)=Δk1+k2x(n)成立.


应用前面的定义和性质,易证明下列结论.

1.2 序列型分数阶差分

2 分数阶差分及和分的Z变换公式
定义6[14]设f(n)为一序列, 其中-∞ (1) 定义7[14]序列型分数阶差分可定义为 首先考虑以下差分方程有关初值的问题 (2) 定理8满足初始问题(2)的解是存在唯一的. 唯一性.令y1(n),y2(n)为方程(1)的解, 则h(n)=y1(n)-y2(n)满足方程Δσmh(n)=0及初值条件, 那么h(n)的Z变换为H(z)=0, 故由逆Z变换得h(n)=0, 从而y1(n)=y2(n)成立.证毕. 考虑初值问题 (3) 则有下面基本定理. 定理9假设|f(n,y)|≤M≤∞,且满足|f(n,y2(n))-f(n,y1(n))|≤A|y2-y1|,其中A≤1,则初值问题(3)存在唯一解. 证明 初值问题(3)等价于 (4)
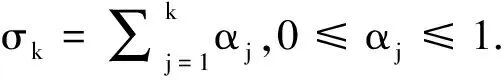

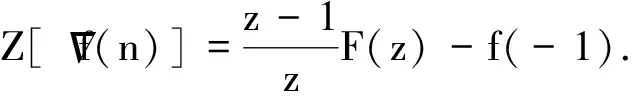
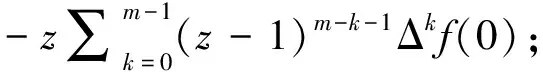



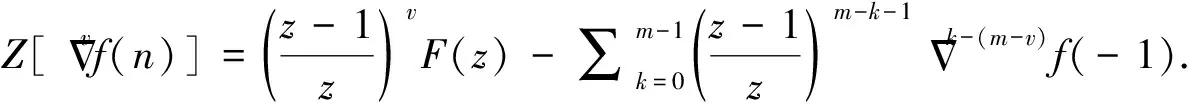

3 序列型分数阶差分方程解的存在唯一性
3.1 序列分数线性差分方程
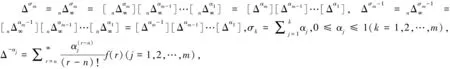
3.2 序列型分数阶非线性差分方程