一种适用于双基SAR的改进PGA方法

陈士超,刘 明,卢福刚,王 军,张 磊

(1.中国兵器工业第203研究所,陕西西安710065;2.陕西师范大学现代教学技术教育部重点实验室,陕西西安710119;3.陕西师范大学计算机科学学院,陕西西安710119;4.西安电子科技大学雷达信号处理国家重点实验室,陕西西安710071)

0 引言

双基合成孔径雷达(Bistatic Synthetic Aperture Radar,BiSAR)由于其在军事应用、资源调查、地壳形变监测等方面的广阔应用前景,受到了越来越多的关注[1-4]。然而相比于单基SAR而言,双基SAR系统的发射天线和接收天线安装在不同的平台上,构型更为复杂,因此较之单基SAR,无论是对成像算法的设计[5-7]还是对运动补偿算法的研究[8-9]都提出了更高的要求。

针对未配备高精度惯性导航系统(Inertial Navigation System,INS)的高分辨雷达成像,研究基于回波数据的运动补偿算法具有重要的应用价值[10-11]。现有的相位梯度自聚焦算法,如标准相位梯度自聚焦(Phase Gradient Autofocus,PGA)算法,对非空变的相位误差具有良好的估计效果,适用于运动误差较小情形的成像处理。针对运动误差较大产生包络偏移及相位误差具有较强空变性的情形,本文提出一种适用于双基SAR成像的改进PGA运动补偿方法。相比传统自聚焦算法,改进的PGA算法同时考虑了运动误差引入的空变相位误差和包络偏移,在具备现有自聚焦技术优点的同时,引入了局部极大似然-加权相位梯度自聚焦(Local Maximum Likelihood-Weighted PGA,LML-WPGA)算法的思想,能高效精确地估计空变的运动误差。实测数据验证了所提出的改进PGA运动补偿算法的有效性。

在诸多双基SAR构型中,一站固定构型是一种相对易于实现的方式。比如,将发射机安装于地球静止轨道卫星上,将接收机安装于机载平台上,这样可大幅度地提高机动飞行器的隐蔽性,同时可以获得更为丰富的目标散射信息,并且具备更高的反隐身能力。本文将一种改进的PGA算法应用到这种构型中,不仅考虑了空变的相位误差,而且也考虑了距离包络的位移偏差。所提算法获得了比传统自聚焦算法更好的误差估计结果,实现了高精度的空变相位误差补偿,获得了更好的双基SAR成像结果。

1 成像几何与信号模型

一站固定式双基SAR的几何构型如图1所示。发射机固定不动,接收机以速度v沿与X轴平行的直线飞行(图1中的理想航迹),接收平台和发射平台的高度分别为hR和hT,R0R和R0T分别表示场景中目标点到接收平台和发射平台的最近距离,RR(η)和RT(η)分别表示场景中任意一点P到接收平台和发射平台的瞬时斜距,η表示方位慢时间,L X和vη0分别表示接收平台和发射平台在成像中心时刻η0沿Z轴方向和X轴方向的最近距离。由于各种非理想因素的存在,发射机不可能完全按照理想的航迹保持严格的直线飞行,图1中的虚线为接收机的实际飞行航迹,不可避免的要产生非理想的运动误差。在η时刻,接收平台天线相位中心位置坐标可表示为[vη+ΔX(η),ΔY(η)+hR,ΔZ(η)],ΔX(η),ΔY(η)和 ΔZ(η)分别对应空间的三维运动误差。

图1 一站固定式的双基SAR几何构型

对于地面上的任意一个目标点P(x,y,z),其斜距历程RΣ(η)为目标点到发射平台和接收平台的斜距之和:

由于发射平台固定,RT(η)不随慢时间η发生变化,有

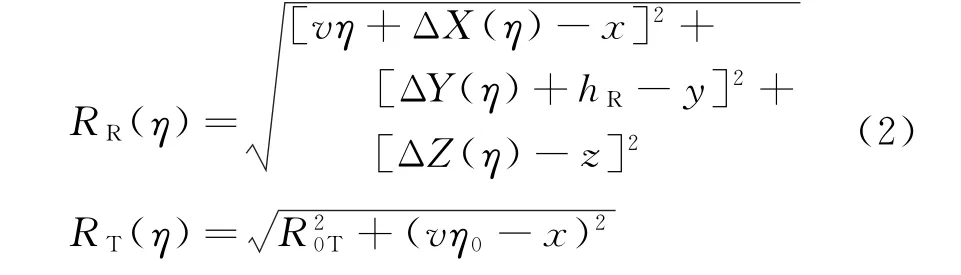
将接收平台对应的斜距RR(η)进行泰勒级数展开,则式(1)表示的斜距历程可表示为

式中:

可见,式(3)将斜距历程分解成两项,RΣ0表示理想条件下双基SAR对应的斜距历程,ΔR表示由于运动误差存在导致的斜距误差分量。式(5)中的第一项表示沿航向的运动误差,第二和第三项为垂直航向的运动误差。基于窄波束和场景为平地的假设[10-11],运动误差的空变性可近似为仅随距离空变,因此式(5)可近似为

2 基于改进PGA的双基SAR运动补偿算法

理想情况下,如前所述,数据录取过程中都假设平台沿严格的直线航迹飞行,所以成像算法仅能够校正理想条件下的距离单元徙动(Range Cell Migration,RCM),而由运动误差导致的非系统RCM(Non-systemic RCM,NsRCM)则需要在运动补偿中进行校正。对于运动误差不大的雷达成像系统而言,NsRCM近似为非空变,即在不同距离范围里,运动误差所引入的RCM可近似被认为是一致的[12]。所以NsRCM对应的包络误差可直接根据距离非空变的相位误差估计得到。假设^ϕec(η)表 示 通 过 相 位 加 权 估 计 PGA(Phase Weighted Estimation-Phase Gradient Autofocus,PWE-PGA)[13]得到的非空变的相位误差,则双基SAR对应的NsRCM为

式中,c表示光速,f表示发射信号的载频。对应的相位补偿函数为

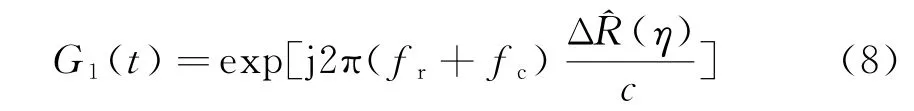
式中,fr表示距离频率。通过式(7)表示的NsRCM校正和相位误差补偿后,剩余的运动误差体现为空变的相位误差。空变的相位误差虽然比非空变部分要小很多,但在某些运动误差较大的成像条件下,有时候忽略空变相位误差的影响仍然足以导致散焦,下面讨论校正剩余空变相位误差的方法。

经过非空变的运动补偿后,双基SAR的剩余距离空变运动误差对应的斜距可表示为

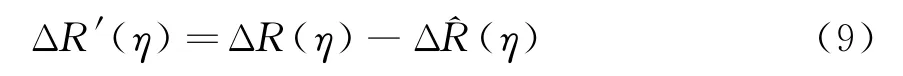
在窄波束和平地假设条件下[10-11],无论是航向的或是垂直航向内的运动误差都可简化为仅是距离空变。将剩余运动误差对应的斜距展开为距离的低阶多项式,有

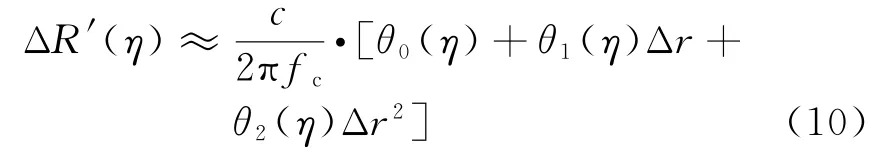
式中,Δr=r-rc,rc表示场景中心点对应的双基SAR斜距之和,θ0(η),θ1(η)和θ2(η)分别表示剩余空变运动误差对应的距离常数项、一次项和二次项系数。需要说明的是,式(10)所表示的运动误差是综合运动误差的距离空变性,自聚焦过程中可对所有误差一起进行估计,包括沿航向方向的运动误差和垂直航向方向的运动误差。通常而言,二阶多项式足以表达剩余运动误差的距离空变性。类比PWE-PGA的加权最小均方(Weighted Least Square,WLS)梯度估计思路,可构建的 WLS估计为

需要说明的是,如果直接采用式(11)进行相位误差梯度估计,将存在和PWE-PGA一样低精度和收敛慢的问题,因为单个距离单元的样本相位梯度估计很难保证高精度,PGA是通过对多样本的相干累加过程保证了其快速收敛性和估计的高精度。剩余相位误差的距离空变是较为缓慢的,在局部距离范围内,运动误差的空变性很小。考虑到相位误差的局部非空变性,对式(11)进行如下的改进,对经过粗补偿的子孔径双基SAR数据进行距离分块处理。假设共分成B块,每一距离块内可认为相位误差不具有空变性,利用第b个距离块中多个距离样本通过加权极大似然PGA(Weighted Maximum Likelihood Phase Gradient Autofocus,WML-PGA)[14]估计式中,G表示此距离块中的距离单元数,h=1,2,…,J表示任意一个方位位置,arg(·)表示取相位函数,conj(·)表示取共轭操作,m b,g表示此距离块中第g个样本单元s b(g,∶)对应的SCR权值。对应第b个距离块的权值w b为

第b个距离块对应的等效距离为

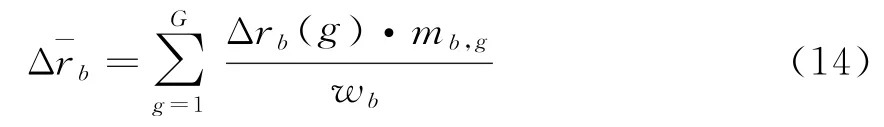
式中,Δr b(g)表示第b个距离块中第g个距离单元所对应的距离。此时多项式的相位梯度估计可更新为

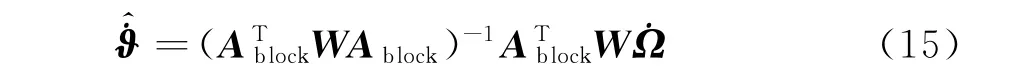
所提出的改进PGA方法可总结如下:首先利用相位误差的局部非空变性,通过WML-PGA得到距离子块内的高精度相位梯度估计,然后利用式(15)估计空变的多项式相位梯度,改进的PGA算法可以实现高精度、高效率的空变相位误差估计。

获得各个子孔径数据的相位误差估计后,进行相位误差拼接得到全孔径相位误差。虽然加权PGA和所提改进PGA中对样本都进行了循环移位,避免引入附加线性的相位,但相邻子孔径之间仍然会存在线性相位差异,全孔径拼接时需要对子孔径之间的线性相位差异进行滤除,相邻子孔径间的线性相位差异可通过子孔径的重叠部分进行估计。最后对全孔径数据进行运动补偿和高分辨双基SAR成像[15]处理。

3 实验结果

以国内某研究所录取的Ku波段一站固定式双基SAR实测数据验证本文所提出的改进PGA算法的有效性,发射机固定于高度约为300 m的山坡上,接收平台的飞行高度约为1 200 m,飞行速度为64.7 m/s,发射机工作状态为正侧视的条带模式。发射信号带宽为80MHz,信号脉宽为10μs,采样频率为100MHz,脉冲重复频率(PRF)为500 Hz。首先以一个子孔径为例,说明空变相位补偿的必要性。图2为实测数据中某一个子孔径数据采用传统的PGA算法估计出的相位误差。由图2可见,相位误差要大于π/4,如果不进行有效的运动误差补偿,直接进行双基SAR成像处理,运动误差将影响最终的成像结果。经过NsRCM校正和非空变的运动误差粗补偿后,运用文中所述的考虑空变运动误差的改进PGA算法,将此块数据沿距离向分成6块,估计此子孔径数据不同距离段数据的运动误差,误差结果如图3所示。由图3可见,粗补偿后,空变的运动误差仍然存在,且在某些距离段中幅度要大于π/4,需要进行空变的运动误差补偿。空变的运动误差补偿后,再次采用传统PGA算法估计此子孔径的运动误差,结果如图4所示。可见运动误差幅度较图2有了明显的减小,此时运动误差幅度的大小明显小于π/4。

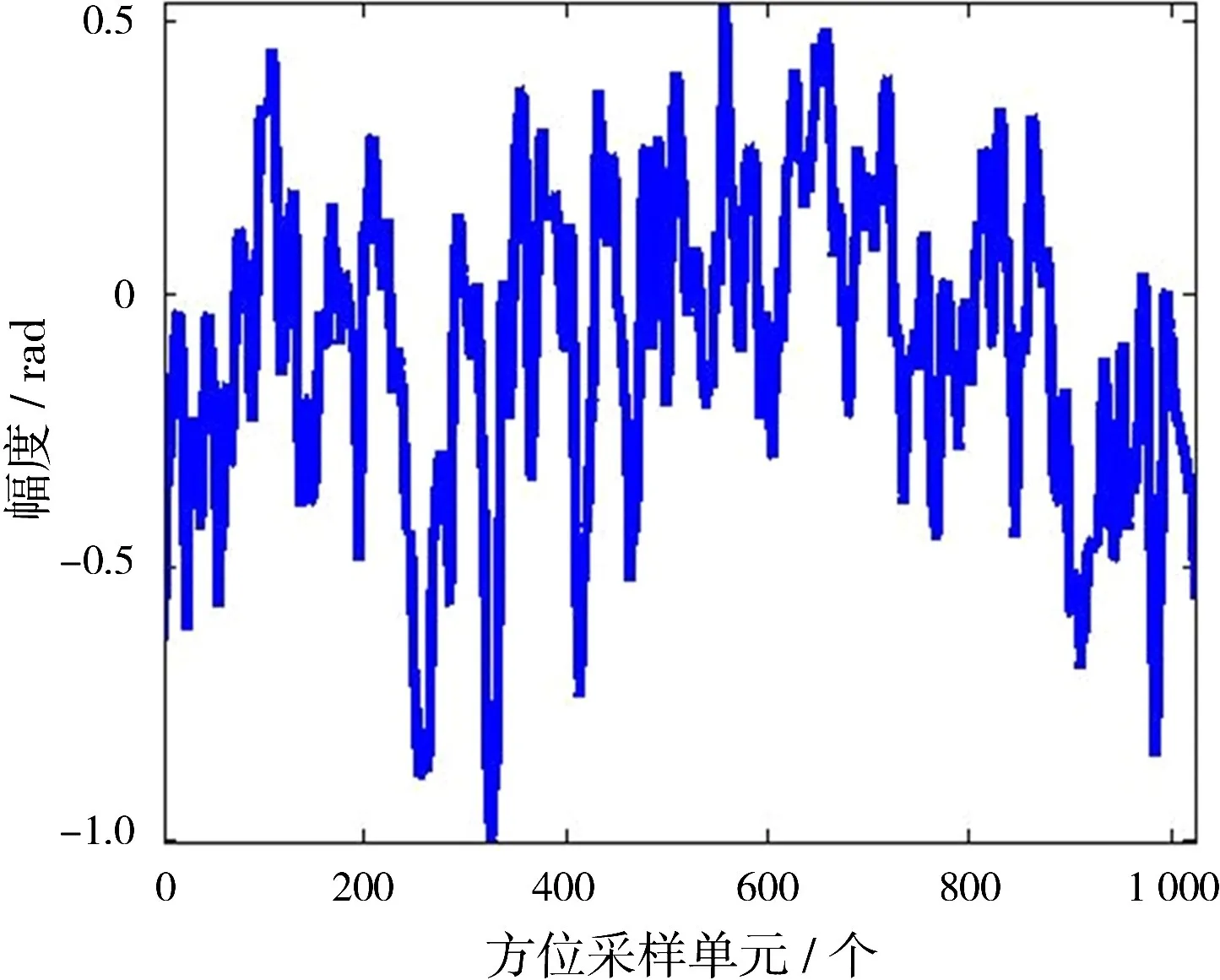
图2 采用PGA估计出的子孔径数据的相位误差

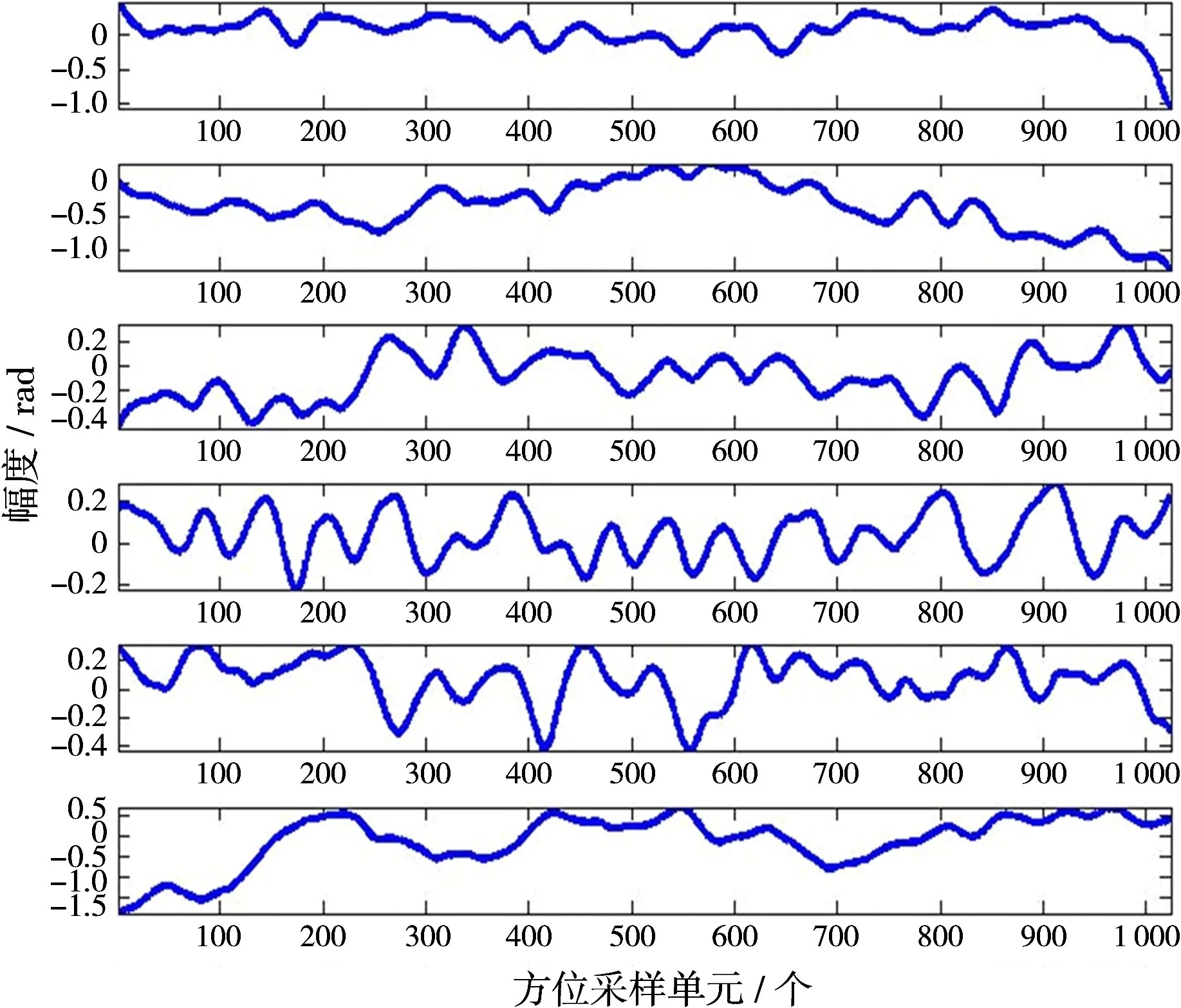
图3 改进PGA估计得到的子孔径不同距离段数据的剩余运动误差

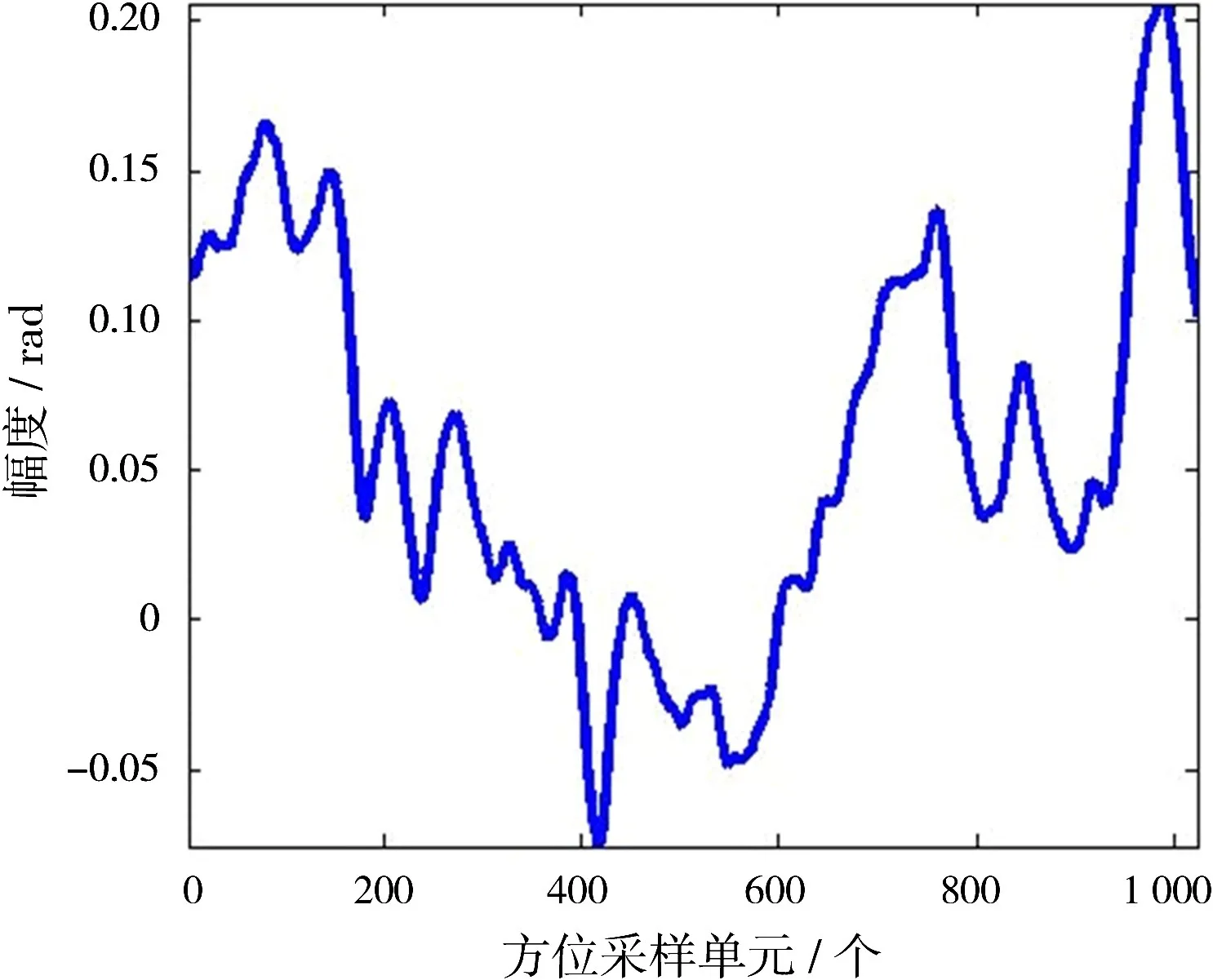
图4 PGA对经空变运动误差补偿后的子孔径数据的相位误差估计结果

需要说明的是,为了获得更好的成像结果,可以继续采用文中所提的改进PGA算法对空变的相位误差进行进一步的估计和补偿。图5为采用文中所提的改进PGA算法获得的大场景聚焦结果,横坐标方向为距离向,纵坐标方向为方位向,可见所提算法可以实现运动误差较大情形下的双基SAR成像。

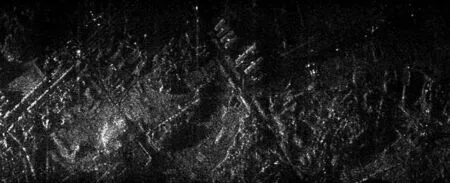
图5 采用改进PGA算法获得的大场景聚焦结果

4 结束语

在运动误差较大的情形下,传统的PGA算法无法获得满意的运动补偿效果。本文提出一种适用于双基SAR成像处理的改进PGA运动补偿算法,充分考虑了运动误差粗补偿后剩余运动误差的距离空变性,将局部似然估计的思想扩展到所提的改进PGA算法中,有效地提升了空变运动误差估计的效率,获得了满意的双基SAR成像结果。需要说明的是,文中仅以一站固定模式对所提改进PGA方法进行了讨论,但其可以推广到更为一般的双基SAR构型中。

[1]ZHAO Y,ZHANG M,ZHAO Y,et al.A Bistatic SAR Image Intensity Model for the Composite Ship-Ocean Scene[J].IEEE Trans on Geoscience and Remote Sensing,2015,53(8):4250-4258.

[2]LUO Y,SONG H,WANG R,et al.Arc FMCW SAR and Applications in Ground Monitoring[J].IEEE Trans on Geoscience and Remote Sensing,2014,52(9):5989-5998.

[3]孟自强,李亚超,邢孟道,等.基于级数反演的双基前视圆周SAR成像[J].雷达科学与技术,2015,13(3):275-283.MENG Ziqiang,LI Yachao,XING Mengdao,et al.Imaging for Bistatic Forward-Looking Circular SAR Based on Series Reversion Method[J].Radar Science and Technology,2015,13(3):275-283.(in Chinese)

[4]马彦恒,宋瑶,董健.空地双基地雷达空间同步研究[J].雷达科学与技术,2015,13(1):65-69.MA Yanheng,SONG Yao,DONG Jian.Research on Spatial Synchronization in Air-Ground Bistatic Radar[J].Radar Science and Technology,2015,13(1):65-69.(in Chinese)

[5]SUN Z,WU J,PEI J,et al.Inclined Geosynchronous Spaceborne-Airborne Bistatic SAR:Performance Analysis and Mission Design[J].IEEE Trans on Geoscience and Remote Sensing,2016,54(1):343-357.

[6]ZENG T,ZHU M,HU C,et al.Experimental Results and Algorithm Analysis of DEM Generation Using Bistatic SAR Interferometry with Stationary Receiver[J].IEEE Trans on Geoscience and Remote Sensing,2015,53(11):5835-5852.

[7]陈士超,邢孟道,保铮.一种同轨双基SAR的非线性CS成像算法[J].西安电子科技大学学报:自然科学版,2014,41(3):1-7.

[8]RIGLING B D,MOSES R L.Motion Measurement Errors and Autofocus in Bistatic SAR[J].IEEE Trans on Imaging Processing,2006,15(4):1008-1016.

[9]ZHOU S,XING M,XIA X,et al.An Azimuth-Dependent Phase Gradient Autofocus(APGA)Algorithm for Airborne/Stationary BiSAR Imagery[J].IEEE Geoscience and Remote Sensing Letters,2013,10(6):1290-1294.

[10]ZENG L,LIANG Y,XING M,et al.A Novel Motion Compensation Approach for Airborne Spotlight SAR of High-Resolution and High-Squint Mode[J].IEEE Geoscience and Remote Sensing Letters,2016,13(3):429-433.

[11]XING M,JIANG X,WU R,et al.Motion Compensation for UAV SAR Based on Raw Radar Data[J].IEEE Trans on Geoscience and Remote Sensing,2009,47(8):2870-2883.

[12]YANG L,XING M,WANG Y,et al.Compensation for the NsRCM and Phase Error After Polar Format Resampling for Airborne Spotlight SAR[J].IEEE Geoscience and Remote Sensing Letters,2013,10(1):165-169.

[13]THOMPSON D G,BATES J S,ARNOLD D V,et al.Extending the Phase Gradient Autofocus Algorithm for Low-Altitude Stripmap Mode SAR[C]∥IEEE International Geoscience and Remote Sensing Symposium,Hamburg:IEEE,1999:564-566.

[14]DE MACEDO K A,SCHEIBER R,MOREIRA A.An Autofocus Approach for Residual Motion Errors with Application to Airborne Repeated-Pass SAR Interferometry[J].IEEE Trans on Geoscience and Remote Sensing,2008,46(10):3151-3162.

[15]QIU X,HU D,DING C.An Improved NLCS Algorithm with Capability Analysis for One-Stationary BiSAR[J].IEEE Trans on Geoscience and Remote Sensing,2008,46(10):3179-3186.