基于小波与EMD级联的穿墙雷达动目标检测

付庆霞,张 晶

(1.中国电子科技集团公司第三十八研究所,安徽合肥230088;2.孔径阵列与空间探测安徽省重点实验室,安徽合肥230088)

0 引言

随着对公共安全考虑的日益增多,人们迫切需要一种可以对建筑物或掩体内的可疑目标进行外部非入侵式探测的装置,以期获得未知复杂场景内部情况信息。因此穿墙探测雷达应运而生,并在国防以及民用上逐步得到广泛应用,如灾难救援与反恐斗争[1-4]。由于墙体对电磁波的衰减作用,目标的反射回波很弱,提高信噪比是目标检测的途径。小波变换由于具有时频局部化、小波基选择灵活、计算速度快、适应性广等优点,成为信号去噪的一个强有力的工具,用小波去噪可以有效去除噪声而保留原始信号[5-6]。经验模式分解(Empirical Mode Decomposition,EMD)方法是由Huang提出的一种新的信号处理方法[7],该方法从本质上讲是对信号进行平稳化处理,将信号中不同尺度的波动或趋势逐级分解开来,对各个IMF(Intrinsic Mode Function)分量进行特征分析,可以更准确有效地掌握原数据的特征信息,从而重构出有用信息。因此,本文提出了小波变换与EMD联合滤波方法对超宽带穿墙雷达动目标进行检测。

1 信号模型

超宽带雷达接收机收到的信号表示如下:

式中,s(t)为运动目标的反射回波,c(t)为静止物体杂波,n(t)为测量及系统噪声。由于墙体对电磁波的衰减作用,目标的反射回波很弱;受发射功率限制信噪比通常很低,去除静止物体杂波、提高SNR是目标检测的途径。因此,本文提出了小波变换与EMD级联滤波方法对超宽带穿墙雷达动目标进行检测。

2 小波变换与EMD级联滤波检测方法

算法首先输入原始信号利用小波进行去噪,去除高频噪声;再利用EMD将信号依特征尺度分解成从高频到低频的一组固有模态,选出符合人体运动范围内的模态累加求和;最后进行运动目标检测,输出检测结果。算法流程图如图1所示。

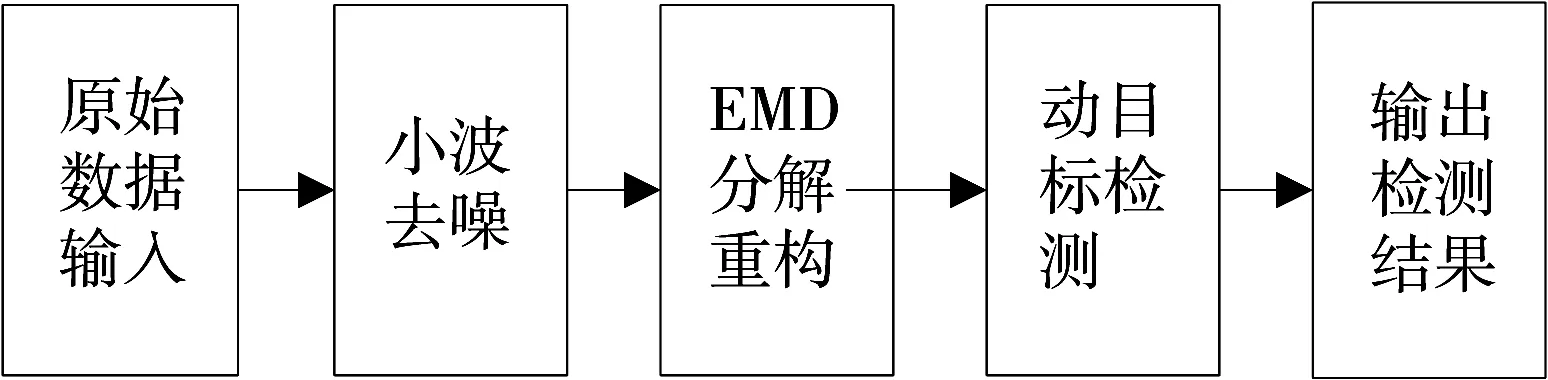
图1 动目标检测算法流程图

2.1 小波多尺度分析

小波分析是现代信号处理中时频分析的常用工具,使用了小波母函数平移和伸缩,小波分析实现了时频分析。母波函数是Ψ(t),伸缩和平移因子分别为a和b,小波基函数Ψa,b(t)定义为

式中,b∈R,a∈R-{0}。信号y(t)∈L2(R)的小波变换定义为

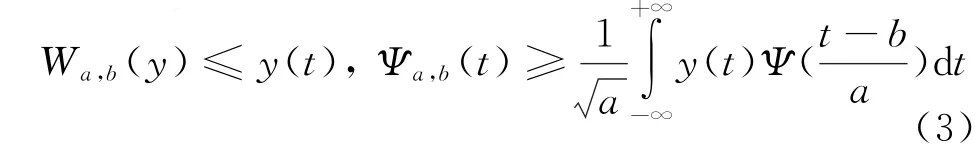
小波变换W a,b(y)就是信号y(t)在对应函数族Ψa,b(t)上的分解,W a,b(y)重构y(t)的小波逆变换定义为

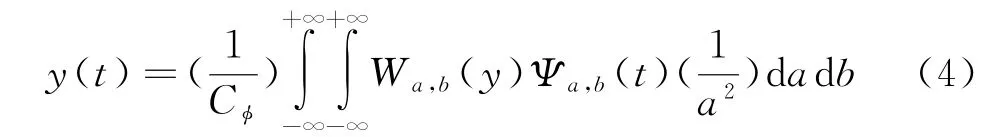
小波基的选择并不是唯一的,只要满足如上容许性条件即可定义所需某一特定信号的小波基。小波变换也可以表示为

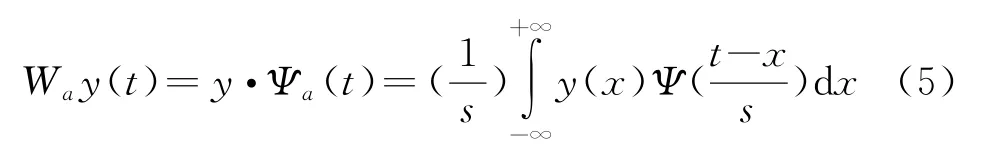
式中,s为尺度参数。在实际应用中,小波变换的尺度参数不必连续取值,而是按照某种方式把连续小波及其变换进行离散化处理。通常对尺度参数s进行二进制离散化,即取s=2j,j∈Z,则y(t)在尺度2j下的小波变换为

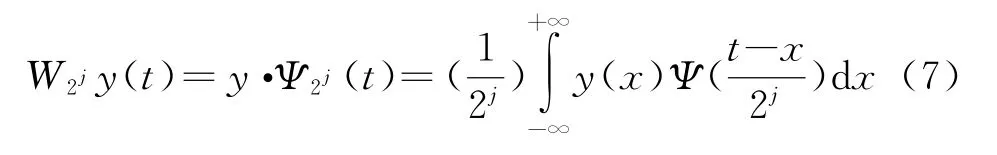
式(7)可以给出第j个倍频程的局部信息。

运动目标信号本质上是一个低频信号,经小波变换后,它的小波变换系数在某些尺度上具有较大的幅值。而噪声的频带大大宽于信号的频带。因此噪声在小波变换系数上的表现与信号相反。根据这种情况,本文利用某尺度下小波变换中的低频系数来重建信号,直接舍弃信号在其他尺度上的系数分量,可使得信号的噪声部分被削弱。

2.2 EMD分解

EMD是希尔伯特黄变换(Hilbert-Huang Transform,HHT)在时域部分的分析方法,这种处理基于波形自身的包络变换,最终能够将信号依特征尺度分解成从高频到低频的一组固有模态函数(或称为本征模态函数)和一个余量的和。分解所得的各个IMF分量反映组成原信号的不同特征尺度,具有准正弦和窄带的特性。这种分解突出了采样数据的局部特征,能够为下一步的分析提供更准确的细部信息。由于EMD是完备和非正交的,处理过程相当于微分运算,不受测不准原理的限制;并且分解过程非线性,所以在时频域上没有交叉项。

EMD的相关理论中指出,当对一个包含高斯白噪声的脉冲回波信号进行分解时,噪声会呈现高频特性[8]。根据算法滤波特性的分析,可以在对回波进行重构时,将前两次分解出来较小的时间尺度分量滤除,同时对其余的IMF分量求和,以达到二次滤除噪声的目的。

EMD方法利用一个迭代的筛分过程将一个给定的信号y(t)分解成L个IMF分量h i(t)和一个残余分量r L(t),每个IMF代表了信号y(t)在某个时间尺度或者频带上的细节。每个IMF要满足两个条件[9]:一是IMF中的极值点和过零点的数目最多相差1,二是上包络线和下包络线的局部均值为0。

筛分过程按照从高频到低频的顺序形成不同阶的IMF,最先得到的IMF(低阶IMF)具有最高的频率,最后得到的IMF(高阶)具有最低的频率。EMD的主要优点是筛分过程是数据驱动的,不需要预先构造基函数。

IMF的筛分过程是一个迭代的过程,每次迭代筛分出一个IMF分量,对于第j次迭代,r j-1(t)为当前残余分量,并且当j=1时,有r0(t)=y(t)。迭代过程如下:

(1)令h j,i(t)=r j-1(t),i=1;

(2)求h j,i(t)的极大值和极小值,并利用3次样条插值求得极大值确定的上包络线和极小值确定的下包络线;

(3)求上下包络线的均值m j,i(t);

(4)更新h j,i+1(t)=h j,i(t)-m j,i(t),t=i+1;

(5)判断h j,i(t)是否满足IMF的两个条件,若满足,则h j(t)=h j,i(t)为第j阶IMF分量,若不满足,重复步骤(2)～(4);

(6)更新残余值r j(t)=r j-1(t)-h j(t),j=j+1,如果r j(t)中的极值点少于两个,终止迭代,否则,从第(1)步开始继续迭代过程。

筛分过程结束后,原信号y(t)可以表示成分解得到的各阶IMFh j(t)和残余值r L(t)的组合:

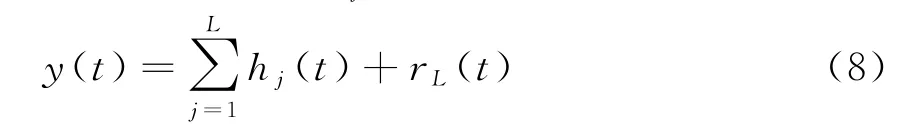
式中,h j(t)代表不同频段的信号分量,r L(t)代表信号整体的变化趋势。

2.3 目标检测算法

本文中目标检测算法应用了文献中的幅度排序点迹凝聚算法[10]。排序器首先对点迹幅度值进行了大小排序,再选择排序后的前m个点迹作为目标的一种估计,本文中m=30。该方法是在质量中心算法的基础上更加突出了幅度值大的点迹,主要是为了避免大量偏离中心的回波较小虚假点迹影响目标凝聚的效果。

3 实验结果与分析

为了检验本文提出方法对超宽带穿墙雷达的动目标检测效果,首先搭建了实验平台,试验场景如图2所示。电子设备包括1个发射天线(图2中位置用Tx表示)、1个接收天线(图2中位置用Rx表示)、1个发射机、多通道接收系统、电源等。穿墙动目标检测试验场景示意图如图2所示,墙体厚度为0.17 m,发射天线和接收天线靠墙并列放置,实验过程中人在墙后来回进行直线匀速运动,运动速度保持0.5 m/s左右。通过接收系统获得实测数据后进行分析。下面为实验获得的原始数据,如图3所示为雷达数据矩阵,横坐标为快时间,即距离维,纵坐标为慢时间,即时间维。对原始数据进行分析发现,除了运动人体回波信号以外,还存在严重的噪声和静物杂波,随着距离增大,运动目标的信噪比急剧下降,最后完全淹没在杂波和噪声之中,根本无法检测跟踪,因此提出了小波变换与EMD联合滤波方法去除噪声和静物杂波。

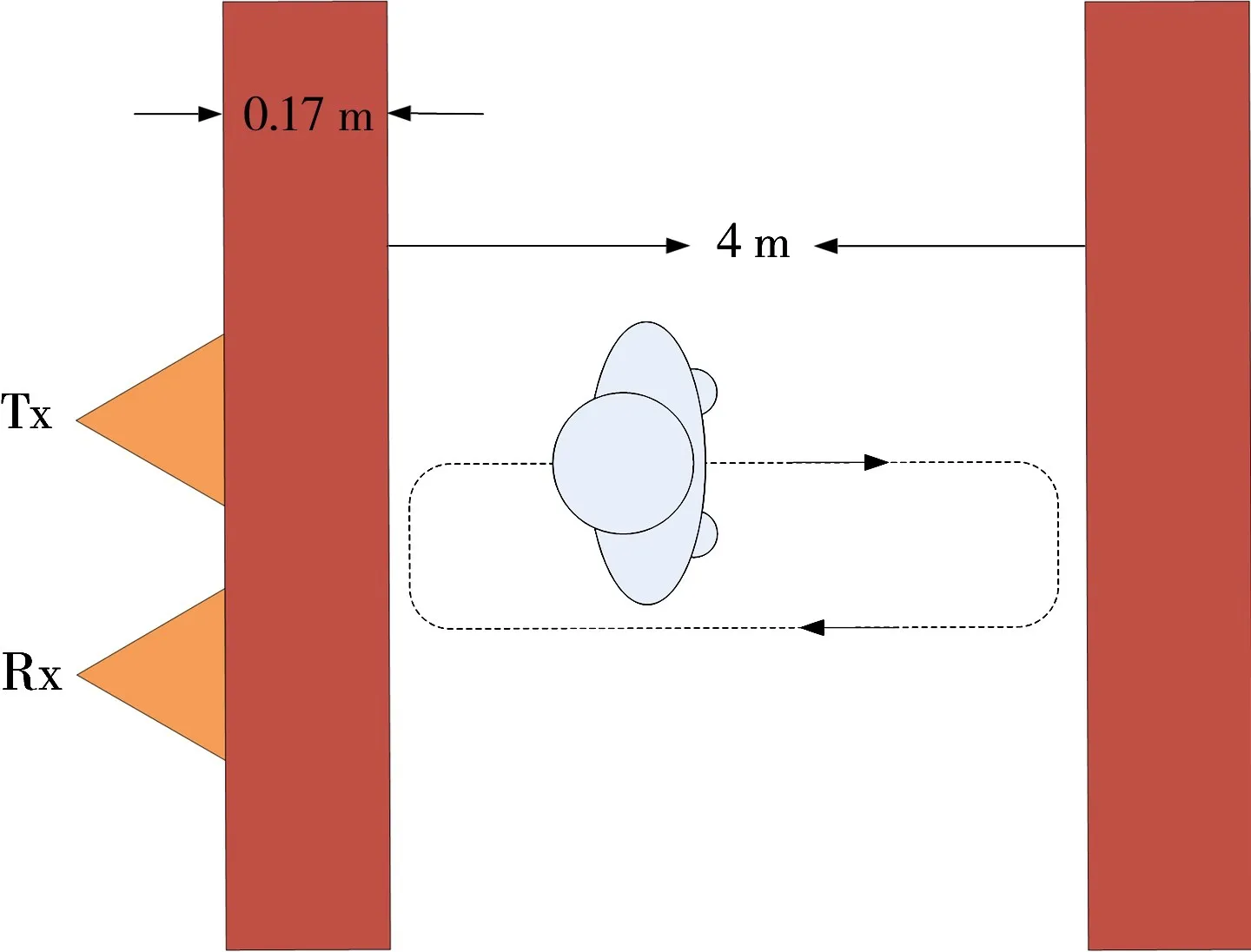
图2 穿墙动目标检测试验场景示意图

从图3可以看出锯齿纹路为人当前时刻所在的位置,图4中可以更清晰地看出提出的算法提高了信噪比。从图3(a)和图4(a)可以看出原始信号运动人体回波信号是淹没在严重的噪声当中的,因此引入了小波的方法进行去噪,从图3(b)和图4(b)可以明显地看出小波去噪以后的数据较原始数据信噪比明显提高了。图3(a)、(b)和图4(a)、(b)中的竖条纹路为静止物体回波,处理后的数据中仍然含有较严重的静止物体杂波,因此引入了EMD分解重构的方法去除杂波,从图3(c)和图4(c)可以明显地看出该方法不仅可以有效去除静物杂波,而且还有二次去噪的作用。

利用提出的小波变换与EMD联合滤波后的数据,进行幅度排序点迹凝聚算法进行目标检测,如图5所示,最终的检测概率为97.39%,获得了非常理想的检测结果。

图4 信号距离与强度关系图

图5 动目标检测结果

4 结束语

本文提出了一种小波变换与EMD联合滤波方法对超宽带穿墙雷达动目标进行检测。该算法首先利用小波去噪方法提高了信噪比;然后应用EMD分解重构的方法,不仅去除静止物体杂波,而且有二次去噪的效果;最后利用幅度排序点迹凝聚算法进行目标检测,本文应用实测数据证明了提出算法的有效性,得到了让人满意的检测结果,具有较好的工程实用意义。

[1]吴世有,丁一鹏,陈超,等.基于超宽带穿墙雷达的目标边界估计算法[J].电子与信息学报,2012,34(6):1277-1283.

[2]YOON Y S,AMIN M G.High Resolution Throughthe-Wall Radar Image Based on Beamspace Eigenstructure Subspace Methods[J].Proceedings of SPIE,2008,6947(1):1-11.

[3]SOLDOVIERI F,SOLIMENE R.Through-Wall Imaging via a Linear Inverse Scattering Algorithm[J].IEEE Geoscience and Remote Sensing Letters,2007,4(4):513-517.

[4]SONG Linping,YU Chun,LIU Qinghuo.Through-Wall Imaging(TWI)by Radar:2-D Tomographic Results and Analyses[J].IEEE Trans on Geoscience and Remote Sensing,2005,43(12):2793-2798.

[5]韦力强,谭阳红,贺迅宇,等.基于新阈值函数的小波阈去噪研究[J].计算技术与自动化,2006,25(4):189-192.

[6]陈小莉,郭静,田茂.小波分析在穿墙雷达回波奇异性检测的应用[J].武汉大学学报(理学版),2010,56(4):487-490.

[7]HUANG N E,SHEN Z,LONG S R.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J].Proceedings of the Royal Society of London A,1998,454(1):903-995.

[8]曹文琛,张顺生.基于EMD的无载波超宽带雷达目标检测算法[J].雷达科学与技术,2013,11(3):285-289.CAO Wenchen,ZHANG Shunsheng.A Target Detection Method Based on EMD for Carrier-Free UWB Radar[J].Radar Science and Technology,2013,11(3):285-289.(in Chinese)

[9]王海梁,熊华钢,吴庆,等.一种改进的基于EMD分解的超宽带信号消噪算法[J].电讯技术,2012,52(4):461-465.

[10]夏栋,夏奎,张伟,等.GPU加速下脉冲压缩雷达的点迹凝聚[J].火力与指挥控制,2013,38(3):81-85.