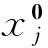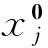基于协同学理论的虚拟企业合作伙伴选择研究

蒲宝山，高诚辉，黄彬

(福州大学，福建 福州 350108)



基于协同学理论的虚拟企业合作伙伴选择研究

蒲宝山，高诚辉，黄彬

(福州大学，福建 福州 350108)

摘要：为最大化虚拟企业项目中各任务间的协同程度，提出了一种基于协同学理论的虚拟企业伙伴选择方法。建立了以极大化系统协同度为优化目标的伙伴选择模型，该模型考虑了系统的交货时间、总费用和产品准时交货率等因素的协同度。此外，针对基本杂草算法在求解伙伴选择模型的过程中容易陷入局部极值的缺点，设计了一种嵌入混沌搜索行为的混合杂草算法来求解该模型。仿真结果表明了该方法的可行性及有效性。

关键词：虚拟企业；伙伴选择；协同度；协同学；混合杂草优化算法

0引言

合作伙伴的选择是虚拟企业构建最为重要的环节之一[1]。国内外学者对此做了大量的研究：Wang等人[2]以成本、交货期及子项目的时序关系为约束，设计了求解该问题的整数规划模型，并用遗传算法求解了该问题。Ip等人[3]考虑了失败风险和交货期等因素，设计了伙伴选择问题的整数规划模型以及求解该模型的遗传算法。Wu等人[4]提出了基于成本和交货期的伙伴选择优化问题，并通过一种两阶段求解方法求解。Zeng等人[5]从成本、工期及子项目时序关系角度考虑了伙伴选择的问题，将问题表示为一个非线性整数规划问题并设计了求解问题的分枝定界算法。Zhao等人[6]考虑了有时序关系的子项目及有交货期约束的伙伴选择问题，以总制造费用最小为优化目标，并设计了粒子群算法对问题进行求解。黄彬等人[7]考虑了模糊完工时间和模糊交货期的情况，基于满意度的概念建立了伙伴选择模型，并采用自适应遗传算法求解模型。Huang等人[8]考虑了满意度、交货期及任务的时序关系等因素，采用Vague集理论建立了伙伴选择模型，并设计了求解该模型的改进粒子群算法。

但是,上述研究均未涉及候选伙伴之间的协同程度。良好的协同程度能够使各个候选伙伴之间任务关系衔接得更加紧密，合作关系更加和谐。在产品的开发过程中，往往需要多个企业之间的相互配合，而盟员企业之间协调性利弊，对产品的开发有直接的影响。哈肯的协同学理论指出：复杂系统内部的不同子系统的各个指标和各个因素的性质对系统的影响是有差异，并且是不平衡的[9]。系统的整体效应是其内部各个复杂子系统协同合作，产生超出子系统自身单独的作用，即实现“1+1> 2”的效应[10,11]。因此，有必要从协同学的角度去定量分析求解虚拟企业的伙伴选择问题。

基于协同学理论，考虑了交货时间、总费用和产品准时交货率等因素，以极大化协同度值为目标，建立了虚拟企业合作伙伴选择的优化模型，并给出了嵌入混沌搜索行为的混合IWO算法。仿真结果表明了该方法的有效性和可行性。

1基于协同学理论的合作伙伴选择建模

1.1问题描述

一个企业接到订单后，由于受到自身生产能力及交货期等各方面因素的限制，其不能在有限的时间内独立完成订单，生产满足客户要求的产品。因此，该企业(盟主)可以将订单分解成若干个具有时序关系的子任务，并且通过竞标方式选择合适的合作伙伴从而组建虚拟企业，共同完成该订单。假设虚拟企业项目可分解为n个具有时序关系的子任务，可表示为V={V1,V2,…,Vn}。如果子任务j只能在子任务i完成之后才能够进行，称子任务i与子任务j为一组相关任务对,用(i,j)表示。其中,(i,j)∈Q,Q是所有相关任务对组成的集合。子任务i有mi个候选伙伴，且每项子任务只能由一个候选伙伴完成。在一定的优化目标要求下，需要选出一组最佳的伙伴组合。

德国理论物理学家哈肯(Haken H)于20世纪70年代创立了协同学，它的基本思想[9]是在开放系统内的生命及非生命的各个子系统，处在一定的条件下时，它们会通过非线性的相互作用，产生一种协同作用和相干成效，并在一定范围内涨落，当达到了临界点时，系统旧的结构就会自组织地在时间、空间及性质等方面发生改变，产生新的有序结构。协同学与虚拟企业合作伙伴选择有着密切的关系。虚拟企业项目可分解为若干个子任务，每个子任务可看作一个子系统，每项子任务均由一个候选伙伴单独完成，根据不同的候选伙伴所提供的竞标参数，每个子系统的有序程度也不尽相同，由此可以产生许多不同的合作伙伴选择的组合方案，因而虚拟企业合作伙伴选择的系统协同程度也不一样。

协同学中，子系统的序参量变量由若干个序参量分量组成，这些序参量分量是刻画子系统运行机制和运行状态的若干个评价指标。子系统的系统有序度刻画了该子系统中各个序参量分量对整个子系统的“总贡献”程度。系统协同度(XTD)是通过子系统的序参量有序度的变化反应整个系统的协同情况[12,13]。XTD∈[-1,1]，XTD值越大,表明该系统的协同发展越好，反之越差。

1.2合作伙伴选择的有序度模型

项目订单可分解为n个时序关系的子任务，子任务Vi由mi个候选伙伴来竞选。其中，n个子任务可看成n个任务子系统，可表示为X={X1,X2,…,Xn}，子系统的序参量ei均由交货时间、总费用及产品准时交货率3个序参量分量构成,ei=(ei1,ei2,ei3),i=1,2,…,n，交货时间包括产品的完工时间与运输时间;总费用则包括产品的制造费用和运输费用。通过对序参量分量——交货时间、总费用及产品准时交货率进行分析，交货时间和总费用是成本型指标，任务子系统的序参量分量的有序度模型表示为[12,13]：

(1)

而产品准时交货率为效益型指标,任务子系统的序参量分量的有序度模型表示为[12,13]：

(2)

其中，αik、βik分别指第i个任务子系统在第k个序参量分量所提供的上限值和下限值，u(eik)∈[0,1]。从总体上看，序参量变量ei对第i个任务子系统的有序程度总贡献可以通过对u(eik)的集成实现。称u(ei)为序参量变量ei子系统的系统有序度，具体模型表示为[12,13]：

(3)

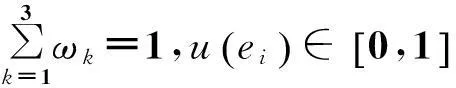
1.3合作伙伴选择的系统协同度模型

设对于给定初始时刻t0，某个任务子系统序参量的系统有序度为u0(ei),i=1,2,…,n,当系统演化到t1时刻，此时任务子系统序参量的系统有序度为u1(ei)，i=1,2,…,n。如果满足u1(ei)>u0(ei)恒成立，则称n个任务子系统构成的合作伙伴选择复合系统从t0到t1是协同发展的，由此定义合作伙伴选择的系统协同度模型为[12,13]：

(4)

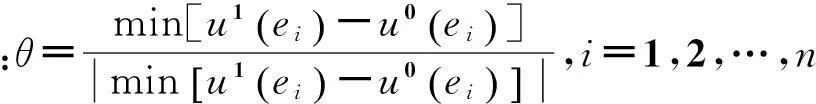
该模型刻画了各个任务子系统之间演化过程的和谐程度。协同度越高，表明了n个任务子系统间协同性越好，默契配合程度越高。

1.4合作伙伴选择的优化模型

以极大化系统协同度为优化目标的虚拟企业合作伙伴选择的模型描述如下：

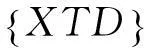
(5)

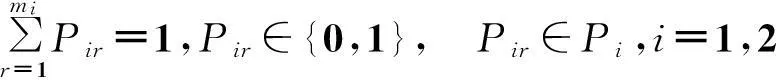
(6)

Sir≤Si

(7)

Fir+Tirjq≤Sjq

i=1,2,...,n;r=1,2,...,mi;q=1,2,...,mj,

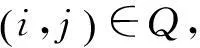
(8)

(9)

其中：Pir=1表明候选伙伴Pir被选中完成子任务Vi，Pir=0则表明候选伙伴Pir未被选中完成子任务Vi；Sir表示候选伙伴Pir计划完成子任务Vi的开工时间；Fir表示候选伙伴Pir计划完成子任务Vi的完工时间；Cir表示候选伙伴Pir完成子任务Vi需要的制造费用；Cirjq表示候选伙伴Pir完成的子任务送到Pjg所需的费用，∀(i,j)∈Q；Tirjq表示候选伙伴Pir完成的子任务送到Pjq所需的时间，∀(i,j)∈Q；Si表示项目要求的子任务Vi计划开工时间；C表示完成该项目的总成本预算；式(5)表示极大化系统协同度；式(6)表示每个子任务务必由相应的候选伙伴中选一个候选伙伴单独完成该子任务；式(7)保证满足子任务的计划开工时间约束；式(8)保证子任务的允许开工时间约束；式(9)保证满足整个项目总成本约束。

2混合IWO算法设计

2.1基本IWO算法

IWO算法由Mehrabian等人于2006首次提出[14]，它是一种模拟杂草入侵过程的群智能算法。IWO算法包含如下四个步骤：

1) 初始化种群：在搜索的范围内随机生成若干棵杂草，并计算出每一棵杂草的适应度值。

2) 生长繁殖：每棵杂草根据他们适应度值大小，按一定比例产生种子，繁衍后代。

3) 空间分布：以均值为0，方差(步长)为d，按一定规律减小的正态分布，在父代杂草个体周围的D维空间进行空间扩散。

4) 竞争生存：经过若干代的繁殖，当杂草总数超过该地所能承受的最大值，淘汰适应度值小的个体，从而满足种群中上限值要求。

IWO算法简单且具有一定的鲁棒性和自适应性，已经在自然科学及工程科学等领域得到了广泛应用。但基本IWO算法也存在算法搜索后期杂草多样性缺乏，局部搜索能力不足，容易出现早熟现象。

2.2嵌入混沌搜索行为的混合IWO算法

针对基本的IWO算法存在的不足，提出了一种嵌入混沌搜索行为的混合IWO算法，在基本IWO算法陷入局部最优解时，在其周围进行了混沌搜索，产生若干组新解，从而增加了搜索后期杂草的多样性，并提高了算法的局部搜索能力。

算法的编码方式采用自然数编码。构造适应度函数如下：

Fit=XTD-γ

(10)

式(10)右边第1项即为目标函数，第2项为惩罚项。其中，当杂草满足式(6)-式(9)所有的约束条件时，惩罚项γ=0；当杂草未满足约束条件时，惩罚项γ为足够大的正值。

2.2.1混沌映射模型

混沌序列是一种非线性的动力系统，它具有很高的伪随机特性，并且本身又是具有不确定性，对初始状态具有很高的敏感性。采用常用的Tent混沌序列[15]：

(11)

其中:r=0,1,2,...，时变参量a满足:0

根据Tent映射模型，在基本IWO算法中嵌入混沌局部搜索策略的具体操作步骤如下：

(12)

式中：[xmin,j,xmax,j]为第j维变量的取值范围，(j=1,2,…,n)。

3) 将上述得到的k个迭代序列的混沌变量按照式(13)映射为原决策变量:

(13)

2.2.2求解伙伴选择问题的混合IWO算法流程

求解伙伴选择问题的混合IWO算法流程见图1。

1) 初始化种群参数，包括初始种群大小N、求解问题维数D、最大迭代次数itermax、最大杂草数目p_size、最大种子数目seed_max、最小种子数目seed_min、非线性因子a、初始标准差si、最终标准差sf、自变量初始搜索空间的最小值及最大值，并根据初始化种群参数，随机产生N组初始解，令迭代的代数iter=1。

图1　求解伙伴选择问题的混合IWO算法流程图

2) 按式(10)计算每一棵杂草个体的适应度值，并根据公式：

(14)

分别计算相应杂草个体能够产生的种子数目。根据公式：

(15)

计算产生新种子的步长。其中，Smax、Smin分别为最大、最小产生的种子数目；Fg、Fw分别为杂草的最好适应度值和最差的适应度值；Fi为相应的第i棵杂草的适应度值。siter为第iter次迭代的标准差值；itermax为最大的迭代次数；a为非线性调和参数；si为起始的标准差值；sf为最终的标准差值。

3) 判断种群的规模是否达到预先设定的最大规模数p_size,若未达到，令iter←iter+1，返回2)。若达到，对上一代杂草父本及下一代的杂草按适应度值的大小进行降序排列，取出前p_size个个体，作为下一代杂草，令iter←iter+1，并选出一个最佳个体，作为当前代的最佳解，进入4)。

4) 判断是否达到最大的迭代代数itermax，若是，转到7)；否则进入5)。

5) 判断是否迭代过程中连续五代的适应度值保持不变，若是，进入6)；否则，转到2)。

6) 取出当前最佳解，并在最佳解的周围进行混沌搜索，搜索到若干组新解，并计算由混沌搜索产生的新解的适应度值，若能够找到一组更好解，则替代之前的最佳解，令其为当前代的最佳解p_best，并转到2)；否则，直接转到2)。

7) 将当前最大适应度值的个体作为最佳解输出，算法结束。

3实例分析及仿真结果分析

3.1实例分析

某制造企业项目可分解成8个子任务，各子任务之间的时序关系如图2所示。企业决定任务1由自己单独完成，其他子任务以投标方式选取候选合作伙伴来完成。经过初选后，子任务V2至子任务V8均有3个候选伙伴。各指标的权值分别为：ω1=0.3，ω2=0.4，ω3=0.3。伙伴选择投标时间数据、伙伴选择投标费用数据、伙伴选择投标的准时交货率情况及各个子任务计划开工时间数据分别如表1-表4所示，项目的成本预算C=65万元。

图2　任务之间的时序关系

任务候选伙伴开工时间/天完工时间/天运输时间/天V1P11S1=0F1=5V2P21S21=5F21=18T2161=4.0T2162=3.0T2163=5.0P22S22=6F22=19.5T2261=5.5T2262=4.0T2263=4.0P23S23=5.5F23=18T2361=2.0T2362=2.0T2363=3.0V3P31S31=6F31=14T3151=1.0T3152=2.0T3153=2.0P32S32=5.5F32=12T3251=2.0T3252=2.0T3253=1.0P33S33=5.5F33=12T3351=2.0T3352=1.5T3353=2.5V4P41S41=5.5F41=14.5T4151=1.0T4152=1.5T4153=2.0P42S42=6F42=12T4251=2.0T4252=1.5T4253=1.5P43S43=5.5F43=12T4351=2.0T4352=1.5T4353=1.0V5P51S51=14F51=21T5161=1.0T5162=1.0T5163=1.0P52S52=15F52=21T5261=1.5T5262=1.0T5263=2.0P53S53=15F53=20T5361=1.5T5362=1.0T5363=2.0V6P61S61=23F61=29T6171=1.0T6172=1.0T6173=0.5P62S62=22.5F62=27.5T6271=2.0T6272=0.5T6273=1.0P63S63=23F63=29T6371=2.0T6372=1.5T6373=1.0V7P71S71=30.5F71=33T7181=2.0T7182=1.5T7183=0.5P72S72=30.5F72=32T7281=1.0T7282=1.0T7283=1.5P73S73=30F73=31.5T7381=0.5T7382=1.0T7383=1.0V8P81S81=34F81=39P82S82=34.5F82=41P83S83=34F83=39.5

表2　候选伙伴投标的费用数据表

表3　候选伙伴投标的准时交货率表

表4　各个子任务计划开工时间数据表

3.2仿真结果及分析

应用以上设计的算法，进行最佳伙伴组合求解，算法中各个参数设置如表5所示。分别将基本IWO算法和混合IWO算法的100次寻优进程的结果进行统计，如表6所示，表明基本的IWO算法收敛于全局最优解的成功率只有88%,而嵌入混沌序列的混合IWO算法100%收敛于全局最佳解，求得协同度值最大的组合方案为[1 3 2 3 3 2 3 1]，即最佳合作伙伴组合为：{P11,P23,P32,P43,P53,P62,P73,P81}，最佳的组合方案下完成该项目的总费用为60.2万元。对两种算法100次运行的结果进行了平均寻优对比，并绘制平均寻优进程的对比曲线图，如图3所示。由图可知混合IWO算法收敛于全局最佳解的速度较快且混合IWO算法比基本IWO算法平均寻优结果高出4.63%。

表5　算法中参数设置

表6　算法收敛数据对比

图3　混合IWO算法、基本IWO算法的平均寻优进程对比

上述结果表明，基于协同学理论建立的合作伙伴选择的优化模型能够成功解决虚拟企业合作伙伴选择的问题，因此，该方法是确实可行的。

4结语

基于协同学理论，建立了虚拟企业合作伙伴选择的优化模型，并设计了嵌入混沌搜索行为的混合IWO算法进行问题求解。当基本IWO搜索陷入局部最优解时，能够在局部最优解的周围进行混沌搜索，提高了基本算法的局

部寻优能力，确保算法最终收敛于全局最优解，通过算例表明了该方法的可行性及有效性，为虚拟企业伙伴选择的研究提供了一种有效的方法。

参考文献:

[1] Talluri S, Baker R C. Quantitative Framework for Designing Efficient Business Process Alliance [C]. //Proceedings of 1996 International Conference on Engineering and Technology Management, Vancouver, BC, Canada, 1996:656-661.

[2] Wang D,Yung K L, Ip W H. A Heuristic Genetic Algorithm for Subcontractor Selection in a Global Manufacturing Environment[J]. IEEE Transactions on Systems Man and Cybernetics Part C- Applications and Reviews, 2001,(31)2,189-198.

[3] Ip W H,Huang M, Yung K L, et al. Genetic Algorithm Solution for a Risk-based Partner Selection Problem in a Virtual Enterprise[J]. Computers&Operations Research, 2003,30(2):213- 231.

[4] Wu N, Su P. Selection of Partners in Virtual Enterprise Paradigm [J]. Robotics and Cornputer intergrated Manufacturing, 2005,21(2):119-131.

[5] Zeng Z B, Li Y,Zhu W. Partner Selection with a Due Date Constraint in Virtual Enterprises[J]. Applied Mathematics and Computation, 2006,175(2):1353-1365.

[6] Zhao Q, Zhang X,Xiao R. Particle Swarm Optimization Algorithm for Partner Selection in Virtual Enterprise[J]. Progress in Natural Science,2008,18(11):1445-1452.

[7] 黄彬,高诚辉,陈亮. 模糊环境下虚拟企业伙伴选择的多目标优化[J]. 中国机械工程,2009,22 (23):2865-2870.

[8] Huang B,Gao C,Chen L. Partner Selection in a Virtual Enterprise under Uncertain Information about Candidates[J]. Expert Systems with Applications, 2011,38(9):11305-11310.

[9] Haken H. Synergetics. From pattern formation to pattern analysis and pattern recognition [J]. International Journal of Bifurcation and Chaos, 1994,4(5):1069-1083.

[10] Harrison J S,Hitt M A, Hosksson R E,et al.Resource Complementarity in Business Combinations: Extending the Logic to Organizational Alliances[J]. Journal of Management, 2001,27(6):679-690.

[11] 郑东,李建华,张欣伟. 汽车制造商与供应商供需系统的协同学分析[J]. 中国软科学, 2010，(3):52-160.

[12] 孟庆松, 韩文秀. 复合系统协调度模型研究[J]. 天津大学学报,2000,33(4):442-446.

[13] 刘志迎，谭敏. 纵向视角下中国技术转移系统演变的协同度研究——基于复合系统协同度模型的测度[J]. 科学学研究, 2012,30(4):534-542.

[14] Mehrabian A R, Lucas C. A Novel Numerical Optimization Algorithm Inspired from Weed Colonization [J]. Ecological Informatics, 2006,1(4):355-366.

[15] Tavazoei M S,Haeri M.Comparison of Different One-dimensional Maps as Chaotic Search Pattern in Chaos Optimization Algorithms [J]. Applied Mathematics and Computation, 2007, 187(2):1076-1085.

Partner Selection in a Virtual Enterprise Based on Synergetic Theory

PU Bao-shan,GAO Cheng-hui, HUANG Bin

(Fuzhou University, Fuzhou 350108, China)

Abstract:To maximize the degree of virtual enterprise synergism between the subtasks in a project, a virtual enterprise partner selection method is proposed based on synergetic theory in this paper. And then, in order to maximize the degree of system synergsim, the partner selection model of this optimization goal is developed, in this model, several factors of the system degree of synergsim are taken into account, such as the delivery time, all-in cost and product on-time delivery rate, etc. In addition, it is well known that, the basic invasive weed optimization algorithm in the process of solving partner selection easily falls in local optimal solution. To deal with this problem, the hybrid invasive weed optimization algorithm is come up with, that the chaos is embeded to solve this problem Finally, the simulation result indicates the feasibility and effectiveness of the proposed method.

Keywords:virtual enterprise; partner selection; degree of synergetic; synergism; hybrid invasive weed optimization algorithm

基金项目：2011年扬州市-扬州大学科技合作资金项目(YZ2011145); 2012年度扬州大学科技创新培育基金(2012CXJ024)

收稿日期：2014-11-22

中图分类号：TH166

文献标志码：A

文章编号：1671-5276(2015)03-0104-06

作者简介：蒲宝山(1986-)，男，福建漳州人，硕士研究生，研究方向为先进制造与敏捷制造。