基于比例风险模型的地铁车门可靠性评估方法研究

何广坚，任金宝，邢宗义

(1. 广州市地下铁道总公司，广东 广州 510030； 2. 南京理工大学，江苏 南京 210094)



基于比例风险模型的地铁车门可靠性评估方法研究

何广坚1，任金宝2，邢宗义2

(1. 广州市地下铁道总公司，广东 广州 510030； 2. 南京理工大学，江苏 南京 210094)

摘要：车门系统作为地铁车辆的关键系统，对车辆的安全性、舒适性有着重要的影响，故引入比例风险模型对车门系统的可靠性进行评估。对车门系统的历史检修数据进行筛选得到协变量因子；应用主成分分析法对协变量进行处理得到协变量矩阵；采用极大似然估计法和牛顿迭代法求取比例风险模型参数估计值；得到车门系统的比例风险模型。通过比例风险模型计算车门系统可靠度下降为0.95时，车门寿命为170天。比例风险模型所得结果与Weibull分布模型所得结果比较，可知比例风险模型所得结果更符合现场工程师经验。

关键词：车门可靠性；比例风险模型；似然估计；牛顿迭代

0引言

车门系统作为地铁车辆的关键系统，对车辆的安全性、舒适性、维护方便性以及整体美观性，有着重要的影响。根据国内外统计，在地铁车辆系统中车门系统的故障占车辆系统总故障的30%以上，对客车运行的安全性构成了严重的威胁[1]。因此对地铁车门系统进行可靠性分析研究，对保证地铁车辆运行安全具有重要的理论意义和实用价值。

针对车门系统这一高故障系统，国内外学者做了大量的可靠性分析研究。朱小娟等[2]采用故障树分析法对车门系统的可靠性进行了分析，得出导致车门故障的所有可能因素和薄弱环节；蔡国强等[3]将GO法的操作符特征量计算方法应用于城市轨道交通车辆车门系统可靠性分析，得出了车门系统的可靠度指标；Thierry Lecomte等[4]对车门控制系统进行可靠性分析，得出控制系统的薄弱环节，用来对控制系统提出改进建议。以上学者的研究为地铁车辆的安全运行做出了贡献，但没有分析车门系统中的日常检修对车门系统寿命的影响。

由于目前尚未检索到检修车门系统寿命预测的相关文献，现引入比例风险模型，将检修数据作为协变量，对车门系统进行可靠性分析研究。首先，将得到的车门系统检修数据进行初步筛选，得到协变量因子；其次，利用主成分分析法对协变量因子进行预处理得到协变量矩阵；然后，利用极大似然估计和牛顿迭代法得到比例风险模型中的参数估计量；最后，得出车门系统的生存函数，预测车门系统寿命。

1比例风险模型

比例风险模型PHM(proportional hazard model)是基于统计回归的寿命预测方法中的一种，最早由Cox在1972年提出[5]，之后很快成为一种统计数据分析工具，并逐步在生物医学领域得到广泛应用。在可靠性工程领域，比例风险模型主要应用于寿命预测和维修时序规划。使用比例风险模型进行设备的剩余寿命预测时，需要完成样本数据处理、参数估计、寿命预测3个基本步骤。首先介绍比例风险模型的基本形式，然后分别在样本数据、参数估计、寿命预测3个方面介绍比例风险模型进行寿命预测的过程。

1.1基本形式

一般地带时变协变量的比例风险模型的函数形式[6]：

(1)

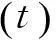
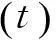
(2)

将式(2)代入式(1)，可得：

(3)

式(3)所示即为地铁车门系统所用的比例风险模型基本形式。

1.2样本数据处理

利用比例风险模型进行寿命预测需要从检修数据中得到以下数据：

a) 设备从开始运行至失效或截尾的时间；

b) 设备从开始运行至失效或截尾过程中的协变量矢量；

协办量是影响比例风险模型的重要因素，协变量选取的结果直接关系比例风险模型的寿命预测准确性，因此对协变量作如下处理。

1) 协变量的预处理

比例风险模型要求各协变量间的偏相关系数尽量小，主成分分析法是一种有效消除相关性的方法，所以可用主成分分析法得到车门系统相互独立的协变量参数。假设车门系统协变量为X1，X2，，Xm，则对协变量数据作标准化处理，得到相关系数矩阵[8]：

(4)

式中，矩阵元素rij(i,j=1,2,,m)为协变量Xi于Xj的相关系数。

利用主成分分析法得到协变量矩阵为：

(5)

2) 协变量综合

由于比例风险模型中的协变量参数有多个，应把原始数据中的多个协变量进行综合，综合协变量函数如式(6)。

(6)

对原始协变量进行线性回归拟合[12]，即：

(7)

可得协变量的综合值如式(8)。

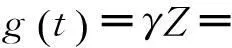
(8)

1.3模型参数估计

极大似然估计具有优良的统计性质和较好的近似分布，同时考虑样本数据中含有截尾数据，故采用极大似然方法来得到模型中各有关参数的估计值[8-12]。

设有n个样本数据，则模型的似然函数为：

lnL(β,η,γ)=

式中：q为失效的样本总数，p为协变量的总个数，k=1, …,p。

采用牛顿-拉夫森(N-R)迭代法求模型参数，假设X=[,,]=[,,1,2, …,m]，对式(9)分别求各参数的一阶偏导数、二阶偏导数和混合偏导数得到矩阵F(X)和矩阵G(X)。

把矩阵F(X)和矩阵G(X)作为迭代因子，利用牛顿迭代公式可得：

(10)

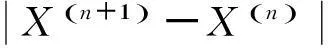
1.4寿命预测

由Weibull分布为基底函数的比例风险模型的失效率函数可得生存函数为：

(11)

由生存函数可得特定可靠度阈值下设备的无故障运行时间。

(12)

由式(11)和式(12)可计算车门系统运行到某一时间段的可靠度和在某一可靠度下车门无故障运行时间。

2实例分析

选取某地铁公司2号线的检修数据，假设年检或架修后则认为车门系统修复如新。通过分析2号线2011~2012年的检修数据，可知在车辆一次寿命周期内正线故障、车辆的维修次数是影响车辆寿命的主要因素，人为因素导致车门无法正常工作也是出现次数较多的因素，因此选取正线故障次数、车辆维修次数以及由于乘客导致的车门故障次数作为车门系统的协变量，如表1。

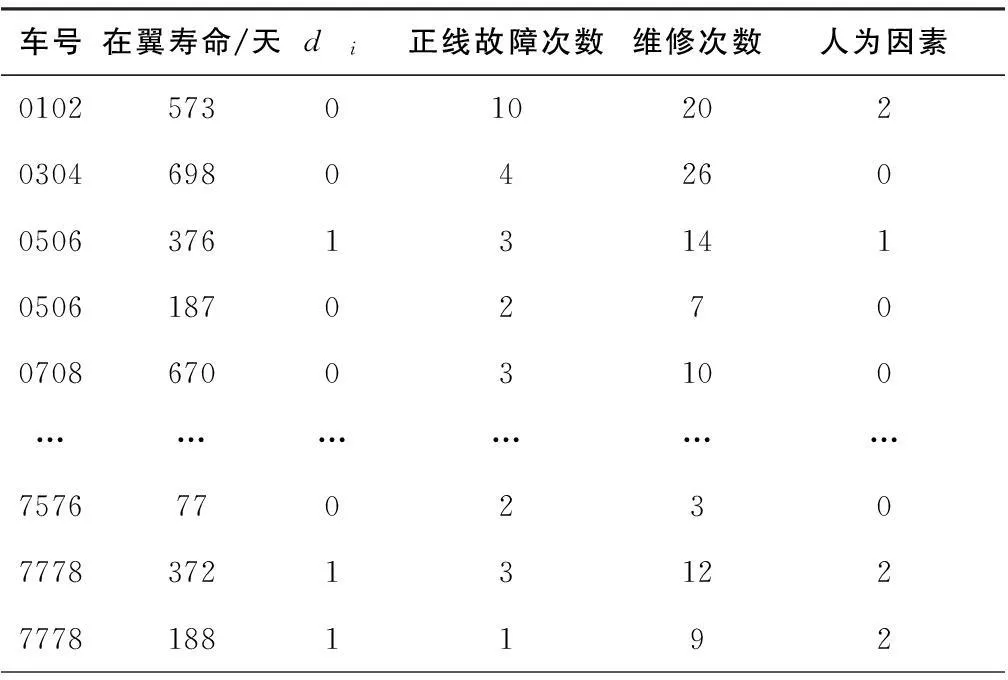
表1　车门系统检修历史记录

续表1

对表1中原始协变量数据进行标准化处理，得到相关系数矩阵

求出矩阵R的特征值和特征向量，得到协变量矩阵：

通过线性回归模型将多个协变量综合成综合协变量影响因子，得到协变量线性回归的拟合结果如表2。

表2　协变量参数的线性拟合结果

结合表1中的数据以及公式(6~10)，选择初始变量X(0)=[2.3，500，-0.12，-0.289，0.03]，可得比例风险模型的参数估计结果如表3。

表3　比例风险模型的参数估计结果

根据表2和表3中参数可得以weibull分布为基底函数的比例风险模型为:

根据失效率函数得到车门系统的生存函数为：

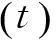
由车门系统的生存函数可得车门系统的可靠度函数图如图1。

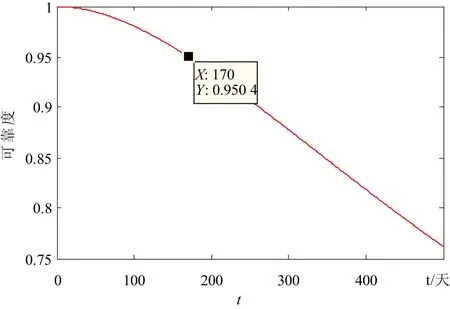
图1　车门系统的可靠度函数图

通过车门系统的可靠度函数计算其可靠度降为0.95时，可靠寿命为t0.95=170天。

对比weibull分布模型和比例风险模型所得车门系统的可靠度函数，可得图2。

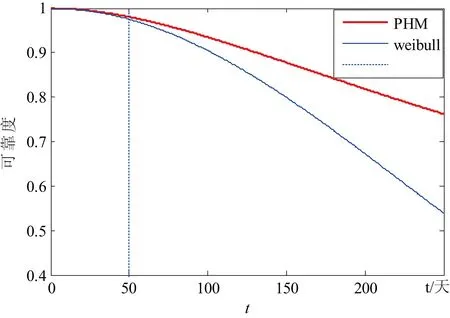
图2　PHM和weibull的可靠度函数图

由图2可知，在初始投入使用的阶段检修对可靠性的影响较小，但两个月后检修可延长车门系统的可靠寿命，所以比例风险模型预测车门系统的可靠寿命比weibull分布模型更加合理。

3结语

通过分析某地铁公司2号线车门系统检修历史数据，引入比例风险模型对数据进行处理，得到了车门系统的可靠寿命t0.95=170天。对比weibull分布可靠性函数模型可知，把检修记录引入可靠性性寿命预测，可使车门系统的寿命预测更符合现场实际，可为地铁维修部门提供技术和管理支持。

参考文献:

[1] 时旭. 地铁车门系统故障诊断与维修决策的方法研究[D]. 北京：北京交通大学,2009.

[2] 朱小娟,王建兵,印祯民. 上海地铁车辆客室车门可靠性技术研究[J]. 城市轨道交通研究,2006,03:31-34.

[3] 蔡国强,周莉茗,李熙,等. 基于GO法的城市轨道交通车门系统可靠性分析[J]. 西南交通大学学报,2011,02:264-270.

[4] Thierry Lecomte. Safe and reliable metro platform screen doors control/command systems[J]. Springer-Verlag, 2008: 430-434.

[5] Cox D R. Regression models and life-tables (with discussion) [J]. Journal of Royal Statistical Society. Series B (Methodological), 1972, 34(2), 187-220.

[6] Mendes, A.C.; Fard, N., Reliability modeling for appliances using the Proportional Hazard Model, Reliability and Maintainability Symposium (RAMS), 2013: 28-31.

[7] E.A.Elsayed. 可靠性工程[M]. 第二版. 北京:电子工业出版社, 2013.

[8] 戎翔. 民航发动机健康管理中的寿命预测与维修决策方法研究[D]. 南京：南京航空航天大学,2008.

[9] 张鹏. 基于主成分分析的综合评价研究[D]. 南京：南京理工大学,2004.

[10] 王文,孟光,刘芳,等. 基于比例风险模型的板级无铅焊点跌落寿命分析[J]. 振动与冲击,2011,(3).

[11] 徐弘博,冯虎田,欧屹. 滚动直线导轨副寿命试验方法[J]. 机械制造与自动化,2014,05:65-68.

[12] 洪东跑,马小兵,赵宇. 基于比例风险模型的可靠性综合评估[J]. 系统工程与电子技术,2010,(10).

欢迎投稿欢迎刊登广告欢迎订阅

Assessment Method of Metro Door Fault Criticality Based

on Proportional Hazard Model

HE Guang-jian1，REN Jin-bao2,XING Zong-yi2

(1. Guangzhou Metro Corporation, Guangzhou 510030,China;

2. Nanjing University of Science and Technology, Nanjing 210094, China)

Abstract:The reliability of Metro Door is directly related to the safety of passengers. The proportional hazard model (PHM) is proposed to evaluate metro door fault criticality. the proportional hazard model is introduced to the description of the relations between reliability and covariates. relevant historical failure data of metro door system, is sifted to obtain the function of the covariates of the model. the log-likelihood function is used to estimate the parameters in the PHM and the Newton-Raphson method is applied to calculating the parameters from the likelihood function. the reliability model is applied to evaluating the lifetime of the metro door. when R is 0.95, the reliable lifetime t0.95is 170. Compared with the Weibull distribution, the PHM is more adaptive and robust and the impact of many covariates is considered simultaneously.

Keywords:metro door reliability; proportional hazard model; likelihood function; newton-raphson

基金项目：苏州市科技发展 (SYG201258)

收稿日期：2015-03-16

中图分类号：U231

文献标志码：B

文章编号：1671-5276(2015)03-0187-04

作者简介：何广坚(1960-)，男，广东顺德人，副总工程师，研究方向：自动控制。