Wendt操作对纽结和链环影响的若干规律
2015-12-27谭秋月孙平安林姝妤
谭秋月,孙平安,林姝妤
(1.武夷学院数学与计算机系,福建武夷山354300;2.厦门大学数学科学学院,福建厦门361000)
Wendt操作对纽结和链环影响的若干规律
谭秋月1,孙平安1,林姝妤2
(1.武夷学院数学与计算机系,福建武夷山354300;2.厦门大学数学科学学院,福建厦门361000)
主要研究在纽结和链环投影图上做一次Wendt操作对纽结和链环的影响,以及其与解结数和交叉指标的关系.定义了与纽结解结数密切相关的一个概念—纽结投影图的拟解结数和2分支链环投影图的拟分拆数,分别计算了纽结表中交叉指标不超过9的纽结和交叉指标不超过8的2分支链环的拟解结数和拟分拆数,并总结了若干经验规律.
纽结;链环;Wendt操作;结数;交叉指标
1 Wendt操作说明
借助于计算机,有人已经对不超过16个交叉点的素纽结的投影图做了完整的同痕分类,对于纽结不计走向与镜像的差别,有下面的表1:

表1 素纽结交叉指标与个数关系
对于两个分支链环,有下面的表2:

表2 两个分支链环交叉指标与个数关系
笔者使用的纽结表和链环表出自Colin C.Adams主编的《The Knot Book》附录中的表.对素纽结表中的投影图做Wendt操作,首先在给定的纽结投影图K(c(K)=n)的交叉点标号,按交叉点个数标上1,2,…,n,然后依照标号依次做Wendt操作.如图1,我们给纽结表中纽结62投影图标上1,2,…,6,我们发现在标号1做Wendt操作,再经过一系列Reidemeister变化,纽结62将转变成31,同理,在标号2做Wendt操作和一系列Reidemeister变化,纽结62也将转变成31,而在标号3做Wendt操作和一系列Reidemeister变化,纽结62将转变成平凡纽结,在标号4,5,6做Wendt操作和一系列Reidemeister变化,纽结62将转变成41.
同样的,对两个分支链环投影图表中的投影图做Wendt操作,首先在给定的链环投影图=的交叉点标号,按交叉点个数标上1,2,…,然后依照标号依次做Wendt操作.如图2,我们给链环投影图的交叉点标上1,2,…,8,我们发现在标号1,2,4,5,6做Wendt操作,再经过一系列Reidemeister变化,链环将转变成,同理,在标号3,7做交叉点做Wendt操作和一系列Reidemeister变化,链环也将转变成,而在标号8做Wendt操作和一系列Reidemeister变化,链环将转变成
2 拟解结数和拟分拆数
定义1对纽结表中的投影图K,先选定其中一个交叉点做Wendt操作,接着做一系列初等变换得到纽结表中的一个新投影图K1,重复以上操作,直到得到平凡纽结投影图.将上述过程所需要的Wendt操作的个数的最小值称为的拟解结数,记为Qu(K)[1].
显然u(K)≤Qu(K).
例如:纽结62的拟解结数为1,因为只需要做一次Wendt操作就可以使纽结62转变成平凡纽结.
在表3,列出了交叉点数少于10的素纽结的解结数及拟解结数.发现交叉点数少于10的素纽结的解结数和拟解结数都相等[2].
一个纽结的解结数也不一定会在它的最少交叉点投影图上找到,下面是同一个纽结108的(图3)两个投影图,一个为最小投影图,另一个则不是,但是左图解结数为3,右图解结数为2.
定义2对2个分支的链环L,给定它的一个投影图,在其部分交叉点上做Wendt操作,总能使得到的新投影图成为L1(可能需要初等变换)分离的[3].考虑L的所有投影图,能实现上述目的的最少交叉点数称为L的分拆数,记为v(L).
类似纽结的拟解结数,对2分支链环定义拟分拆数.
定义3对链环表中有2个分支的投影图L,我们先选定其中一个交叉点做Wendt操作,接着做一系列初等变换得到链环表中的一个新投影图L1,重复以上操作,直到得到可分离的链环.将上述过程所需要的Wendt操作的个数的最小值称为L的拟分拆数,记为Qv(L)[4].
表4中列出了交叉点数少于9的两个分支链环的拟分拆数.
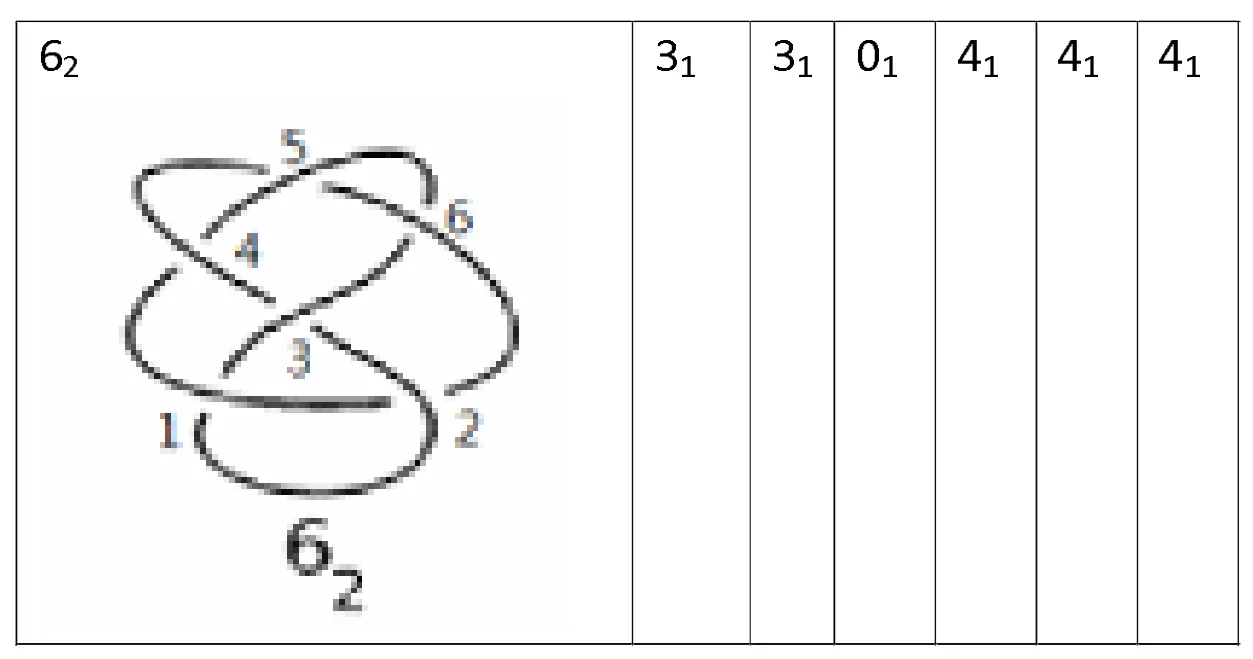
图1 纽结62每个交叉点经过一次Wendt操作的结果
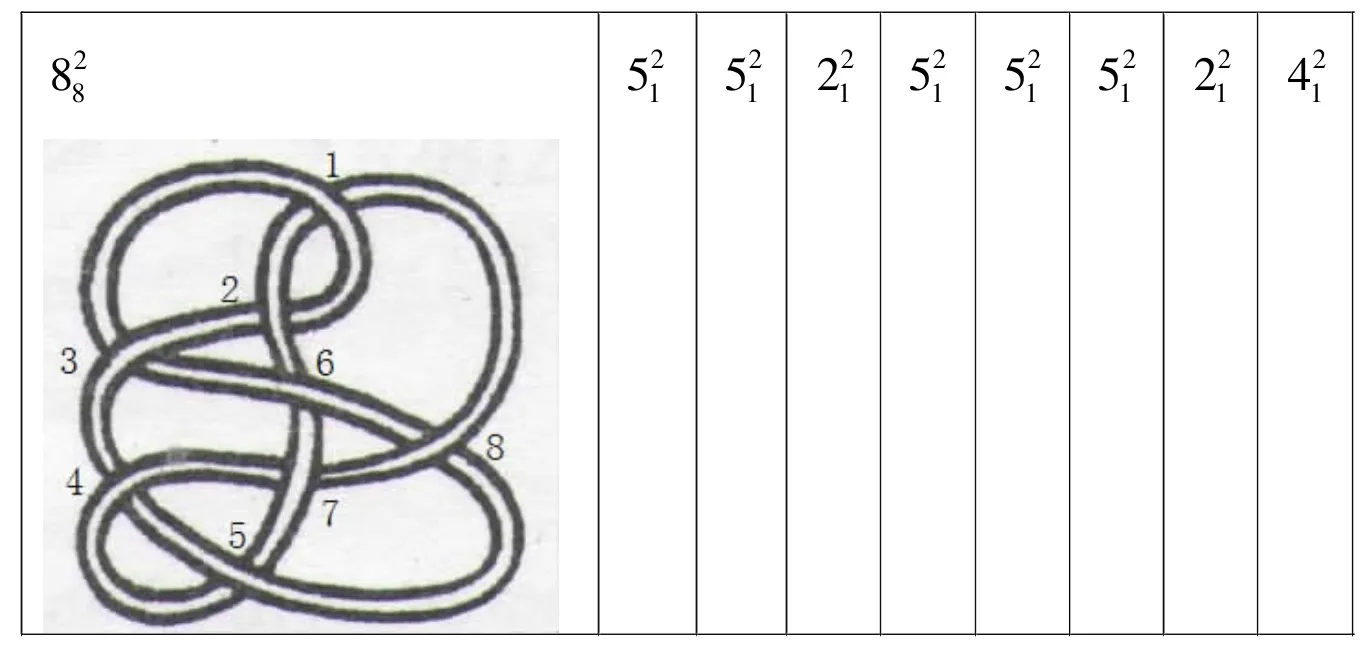
图2 链环每个交叉点经过一次Wendt操作的结果
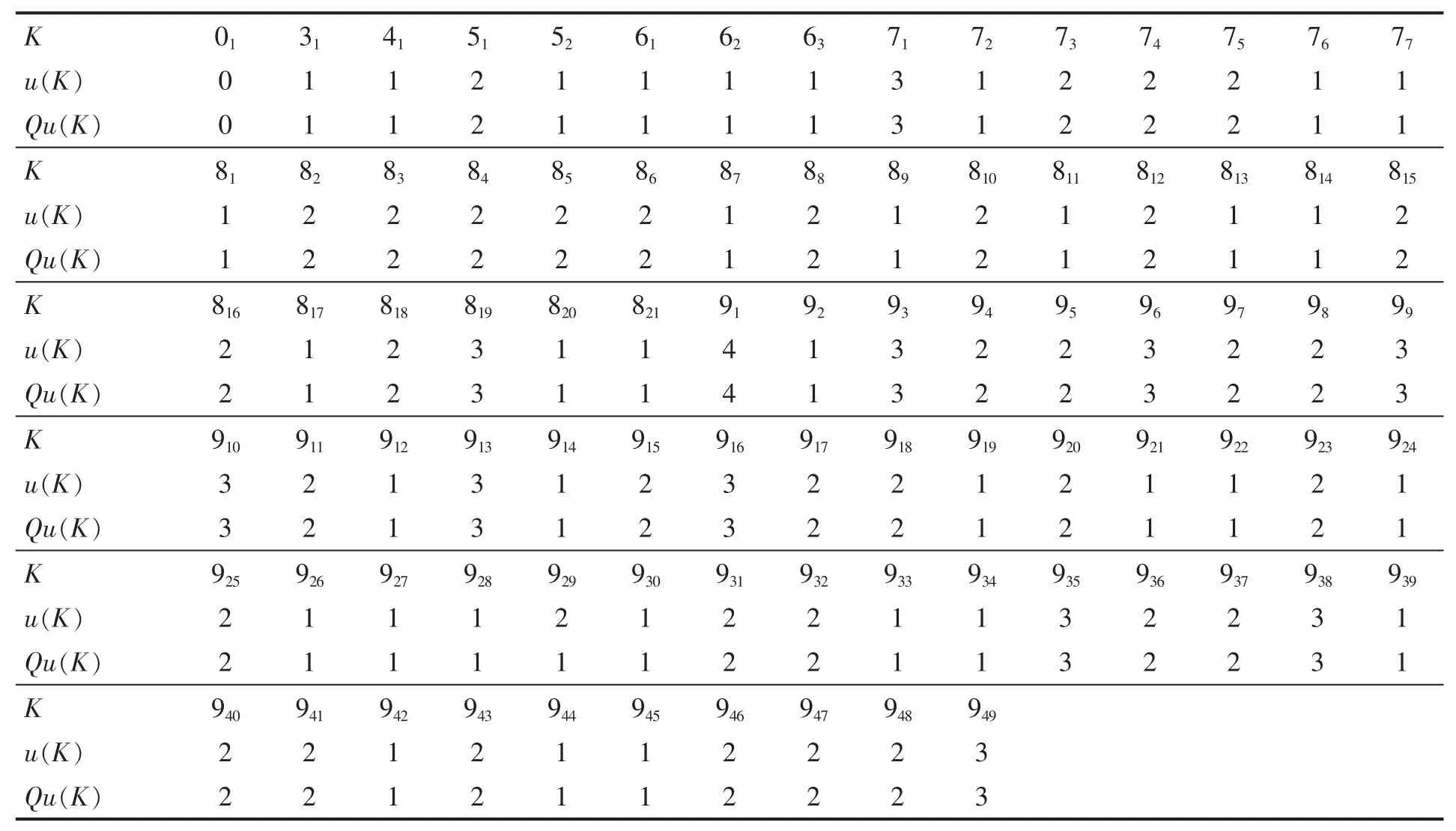
表3 纽结、纽结解结数及拟解结数

表4 链环和链环拟分拆数
以下是与拟分拆数有关的公开问题:
一个交错链环投影图,做一次Wendt操作,在什么条件下得到的投影图将是可分离的,见文献[5].
3 经验规律
规律1在交叉点数少于10的纽结中,我们发现:非交错纽结K的两个交叉点数相同的投影图的每个交叉点上做一次Wendt操作得到的纽结集合不见得会相同,但交错纽结的两个叉点数相同的投影图的每个交叉点上做一次Wendt操作得到的纽结集合则相同[6].
第一行表格与第二行表格分别是纽结943的两个不同投影图,只需做一次R3变化,其交叉点均为9,在9个交叉点上分别做一次Wendt操作,再经过一系列Reidemeister变化,得到的9个纽结是不同的.例如图4.
下面来说明下这两个纽结投影图(图6)是同痕的,注意到红色椭圆区域内tangle是一模一样的的,我们只需说明两个纽结投影图去掉红色区域剩下的部分可以在4条端点固定情况下互相转换即可[7].
把红色部分去掉所得的图7,将其形变为下图8:易看出以上2个只要沿水平线拧360度即可互相得到.由此可以这样说明因此两个814投影图是相同的纽结.
规律2在笔者采取的表中交叉点数少于10的交错纽结投影中,发现对其一个交叉点做Wendt操作,若得到的纽结仍然为交错纽结,则其交叉指标至少减少2.若不是,则不然.对交叉点数少于9的2个分支链环,此结论也成立.
若经过Wendt操作得到的纽结为非交错纽结,则存在减少1的情况.如图9.
规律3若纽结对应的Conway符号为m,n,其中m,n必有一个为偶数,m若为偶数,则其对应的解结数若,n均为偶数,则其对应的解结数如表5.
同样要证≤容易,但是要证明≥就比较难.

表5 Conway符号m,n与解结数之间关系

图4 非交错纽结943两个不同投影图每个交叉点经过一次Wendt操作的结果

图5 交错纽结814两个不同投影图每个交叉点经过一次Wendt操作转变结果
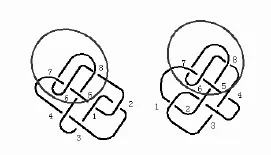
图6 纽结814的两个投影图

图7 纽结814的两个投影图

图8 纽结814的两个投影图

图9 交错纽结933每个交叉点经过一次Wendt操作的结果
[1]BOLLOBASB.ModernGraphTheory[M].Berlin:Springer,1998.
[2]KAWAMURAT.TheUnknottingNumberof10139and10152are4[J].OsakaJ.Math.,1998,(35):539-546.
[3]STOIMENOW A.Polynomial Values,the Linking form and Unknotting Numbers[J].Mathematical Research Letters,2004,32(4):139-141.
[4]JungHoonLee.CriticalHeegaardSurfacesObtainedbyAmalgamation[J].TopologyanditsApplications,2013,160(1):135-138.
[5]ADAMSCC.TheKnotBook[M].AmericanMathematicalSociety,2004:143.
[6]姜伯驹.绳圈的数学[M].长沙:湖南教育出版社,1991:5-24.
[7]REIDEMEISTERK.ElementareBegrundungderKnotentheorie[J].Abh.Math.Sem.Unic.Hamburg.,1926,(5):24-32.
(责任编辑 李健飞)
Some Results of the Unknotting Number and Crossing Number Based on Wendt Operation
TAN Qiu-yue1,SUN Ping-an1,LIN Shu-yu2
(1.Department of Mathematics&Computer,Wuyi College,Wuyishan,Fujian 354300,China;2.School of Mathematical Sciences,Xiamen University,Xiamen,Fujian 361000,China)
This paper studies the effect of a single Wendt's operation on knot and link diagrams and its relation with the unknotting number and the crossing number.It introduces two notions for link diagrams,namely Quasi-unknotting number and Quasi-splitting number,calculates these two numbers for knots with crossing number no more than 9 and 2-comonent links with crossing number no more than 8,respectively,and finds some empirical regularities.
knot link;Wendt's operation;unknotting number;crossing number
O157.5
:A
:1673-1972(2015)06-0061-06
2015-07-13
福建省青年教师专项(JA1551);福建省教育厅科技项目(JK2012056);武夷学院青年教师专项(xq201110)
谭秋月(1980-),女,陕西杨凌人,讲师,主要从事图论、离散数学研究.
