虚拟链环的Kauffman尖括号多项式的Maple计算

李美莲,邓青英

(1.厦门大学数学科学学院,福建厦门361005;2.龙岩学院数学与计算机科学学院,福建龙岩364000)

虚拟链环的Kauffman尖括号多项式的Maple计算

李美莲1,2*,邓青英2

(1.厦门大学数学科学学院,福建厦门361005;2.龙岩学院数学与计算机科学学院,福建龙岩364000)

将Itik和Banks对经典链环的Kauffman尖括号多项式的计算方法推广到虚拟链环,算法使用了圈置换的方法计算虚拟链环投影图的每一种状态下的圈的个数.所谓虚拟链环投影图的状态是指对投影图中每个经典交叉进行A-smoothing或B-smoothing操作,而对虚拟交叉点采用直走的两条小弧线代替后所得的结果.利用Maple软件编写出了该算法的程序,可以实现任意一个虚拟链环的Kauffman尖括号多项式的计算.

虚拟链环;Kauffman尖括号多项式;Maple程序

1 预备知识

文献[1-2]引进了虚拟纽结理论,它是经典纽结理论的推广.一个虚拟链环投影图本质上是一个带有标记为虚拟交叉点的链环投影图.一般地,一个虚拟链环投影图由n个分段线性的闭合平面曲线组成,在这些曲线中有有限个重点,并且在每个重点正好两段弧线交叉穿过.每个重点或者是一个经典的交叉结构(图1(a))或者是一个虚拟交叉结构(图1(b)).一个虚拟链环指的是虚拟链环投影图在广义Reidemeister变换下的等价类.

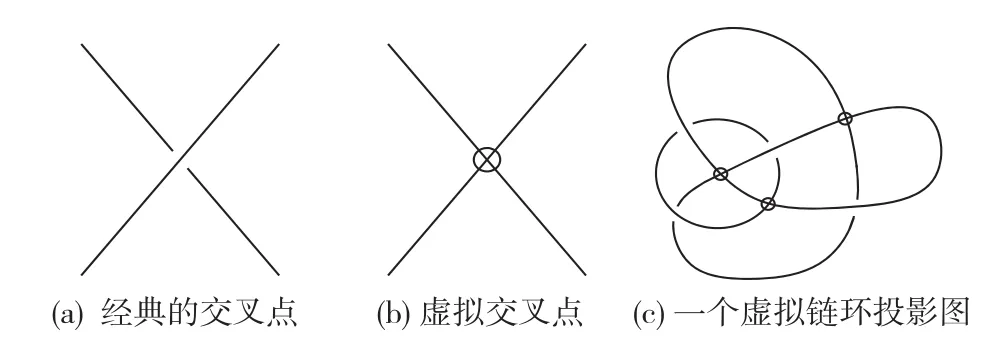
图1 虚拟链环投影图Fig.1 Virtual link diagrams

正如链环投影图一样,为了美观,把虚拟链环投影图画成光滑的(如图1(c)).需要强调的是虚拟交叉点没有上线,下线的交叉结构,这种交叉不是原投影图(投影到曲面上)本身结构的部分,而是将其画到平面上时产生的.

设L是一个虚拟链环投影图,令φ(L)为经典交叉点的集合,L的一个状态s是指一个φ(L)到{A,B}的函数,即给L的每个经典交叉点指定一个标记A或B.L的所有状态构成的集合记为ψ(L).

将投影图L中的一个经典交叉点邻近的4个区域分为两个A区域,两个B区域,其中上行线按逆时针方向转至下行线所扫过的两个区域为A区域,另两个区域为B区域(见图2(a)).

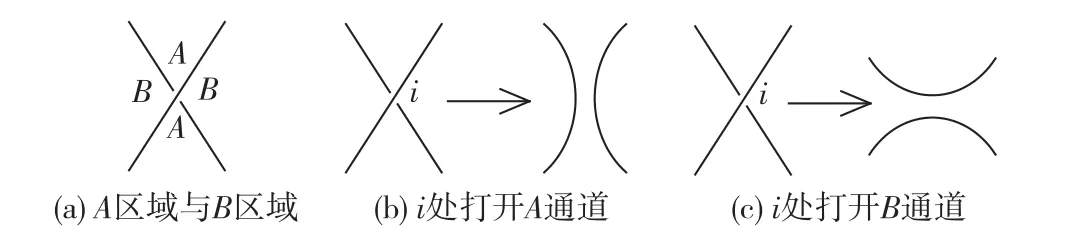
图2 A区域与B区域与打开Fig.2 A regions and B regions and openings

从投影图L按图2(b)所示方法得到投影图L′,称之为将L在交叉点i处打开A通道(即进行A-smoothing操作)而得到的投影图.从投影图L按图2 (c)所示方法得到投影图L′称之为在交叉点i处打开B通道(即进行B-smoothing操作)而得到的投影图.

对一个投影图L与一个状态s∈ψ(L),令L|s为将L在每个经典交叉点i处打开s(i)通道而得到的投影图(i∈φ(L)).注意,L|s是一组圆圈的分离并(从曲面上看).记c(s)为L|s的圈的个数,α(s),β(s)分别为s中标记为A,B的交叉点个数.

定义1 设L是一个虚拟链环投影图,定义L的Kauffman尖括号多项式〈L〉∈Z[A,A-1]为

Kauffman尖括号多项式是由Kauffman在文献[3]中对经典链环引入的一个多项式并在文献[1]中将其推广到虚拟链环.它是著名的Jones多项式的主要部分,也是计算Jones多项式的困难所在.

文献[4]提出了计算经典链环投影图的Kauffman尖括号多项式的一种新方法,即使用圈置换的方法来计算经典链环投影图的每一种状态下的圈数.本文注意到该方法可推广到虚拟链环,并用Maple软件编写出了计算程序.

2 方 法

考虑一个具有N个经典交叉点的虚拟链环投影图,在每个经典交叉点放置一个小圆圈,小圆圈里没有任何其他交叉点.对小圆圈与投影图弧段(经典交叉点之间的连线)的交点按如图3(a)从上线开始依顺时针方向递增进行标号.

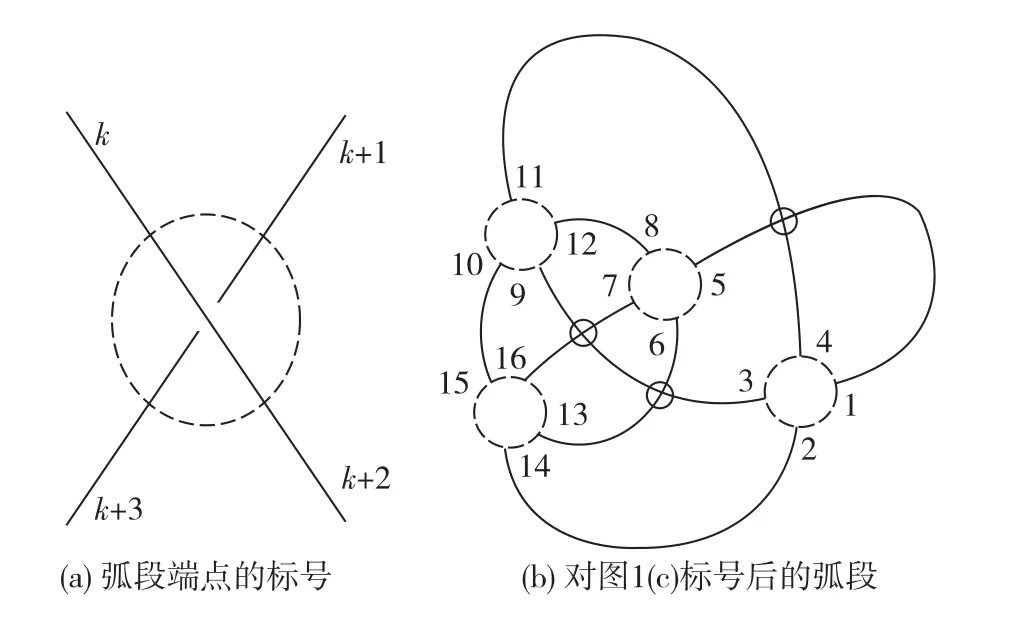
图3 弧段端点的标号与图1(c)标号后的弧段Fig.3 Numbering end points of arcs and numbered arcs from Fig.1(c)

由于假设有N个经典交叉点(或称为节点),所以链环投影图有2N条弧段且共有4N个弧段的端点,对这些端点1,2,3,…,4N进行标号.把集合{1,2,3,…4N}分成2N个子集{A1,A2,A3,…A2N},这里Ai={i1,i2},并且i1,i2是一条弧段的两个端点的标号,其中i2＞i1.把上述情况写成数组形式,记为P1

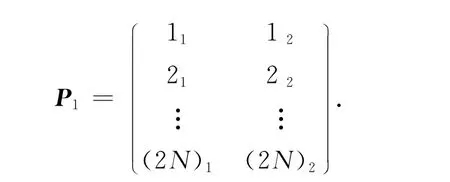
注意到这个数组中,每个数ij∈{1,2,3,…,4N},且这个集合里的每个数在这个数组中恰好出现一次.下面考虑一个具体例子.对图1(c)的虚拟链环投影图,若按图3(a)所示给它进行标号,则P1等于下列所示的数组.

另外,按顺时针的顺序从标号最小的上线开始标记逐个节点周围的端点,可以得到另外一个数组构成的2N×2阶矩阵,记为P2.

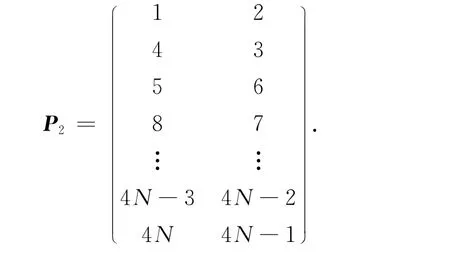
对应图3(b)的P2为下列所示的数组.

在数组P2中,1连接2,3连接4等等,按这种方式,P2对应的就是全A状态.如果对节点1选择B-smoothing操作,则需将P2变为P′2

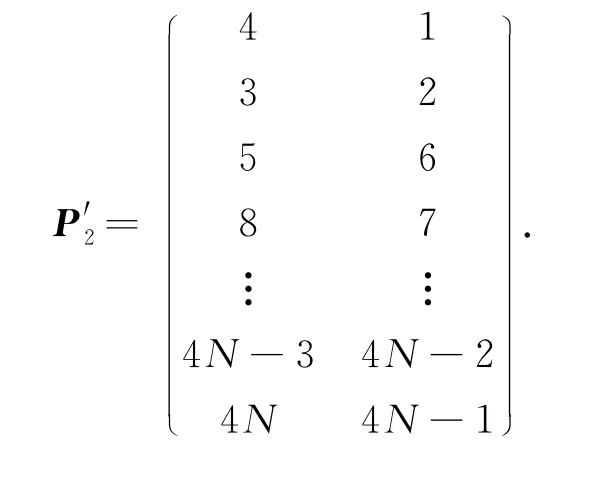
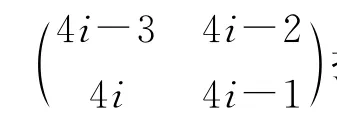
假定数组P1是固定的.给定一个对应某个状态s的P2,从P1开始选取11,令σ(11)=12,然后从P2中找到12,写σ(12)=l2.这里l2是P2中与l2同一行的另一个数.再回到P1,从P1中找到l2,写σ(l2)=k2,其中k2为P1中与l2同一行的另外一个数,如此一直下去,可以获得集合{1,2,3,…,4N}的一个置换σ,这个置换的每个圈对应于状态s下的一个圈,这个置换的圈数正好就是c(s).

例1 考虑虚拟链环投影图1(c)的BBAB状态,如图4.

图4 虚拟链环投影图1(c)的BBAB状态Fig.4 A state BBAB of the virtual link diagram Fig.1(c)

对应于图4的P2为:

与该链环投影图相关的置换为

即置换

(1 5 8 12 11 4)(2 14 15 10 9 3)

(6 13 16 7).

表1 图1(c)的圈置换Tab.1 Cyclic permutations for Fig.1(c)

3 程 序

通过将第2节中的求c(s)的方法转换成求图的分支数我们用Maple软件编写了计算虚拟链环的Kauffman尖括号多项式的程序.程序中输入的3个参数P,K,N的解释如下:数组P表示上文中的数组P1,矩阵K表示全A状态下的数组P2,N表示所有经典节点的数目.

程序中几个重要变量的解释如下:矩阵Q的初始值是2N×2阶零矩阵,通过将第i个经典节点的状态值赋给矩阵Q的4个元素Q[2i-1,1],Q[2i-1,2], Q[2i,1],Q[2i,2].若第i个经典节点的状态是A-smoothing,则将矩阵K相应的4个元素赋给矩阵Q的4个元素;若第i个经典节点的状态是B-smoothing,则先将矩阵K相应的4个元素顺时针旋转90°再赋给矩阵Q的4个元素;从而矩阵Q表示虚拟链环投影图的一种状态,即同上文中的数组P'2.程序中数组P的每一行看成图Gr P的一条边,矩阵Q的每一行表示在相应状态下小圆圈中的一段弧,将Q中的所有弧段当作边加入到图Gr P中得到的新图记做图Gr PQ,通过命令ConnectedComponents(Gr PQ)求出图Gr PQ中的连通分支Comp,即上文中由数组P1和P'2所得到的置换的圈分解.连通分支数记做c,即置换中圈的数目.根据Kauffman尖括号多项式的计算公式,对每个状态对应的的w·dc-1进行求和,其中b是第j(1≤j≤a)个状态中A-smoothing的数目,w=Ab·A-(N-b).

4 实 例

例2 根据Maple程序求图1(c)的虚拟链环投影图的Kauffman尖括号多项式.

输入 J 1∶=Virtual Link(Matrix([[1,5],[2,14],[3,9], [4,11],[6,13],[7,16],[8,12],[10,15]]),Matrix([[1,2], [4,3],[5,6],[8,7],[9,10],[12,11],[13,14],[16,15]]),4)

例3 根据Maple程序求图5(a)的虚拟链环投影图的Kauffman尖括号多项式,标号如图5(b).

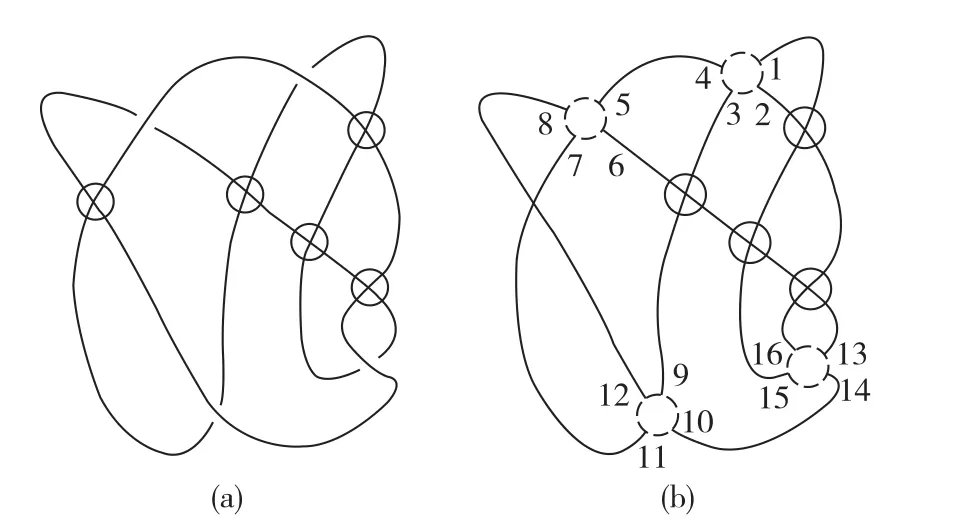
图5 纽结4.93[5]Fig.5 The knot 4.93[5]

输入 J 2∶=Virtual Link(Matrix([[1,15],[2,12],[3, 5],[4,14],[6,16],[7,10],[8,11],[9,13]]),Matrix([[1,2], [4,3],[5,6],[8,7],[9,10],[12,11],[13,14],[16,15]]),4)

例4 根据Maple程序求图6(a)的虚拟链环投影图的Kauffman尖括号多项式,标号如图6(b).

输入 J 3∶=Virtual Link(Matrix([[1,25],[2,5],[3, 16],[4,8],[6,27],[7,9],[10,22],[11,14],[12,13],[15, 17],[18,21],[19,24],[20,26],[23,28]]),Matrix([[1,2], [4,3],[5,6],[8,7],[9,10],[12,11],[13,14],[16,15],[17, 18],[20,19],[21,22],[24,23],[25,26],[28,27]]),7)

图6 虚拟链环投影图[6]Fig.6 The virtual link diagram[6]

[1] Kauffman L H.Virtual knot theory[J].Eur J Combin, 1999,20:663-691.

[2] Goussarov M,Polyak M,Viro O.Finite type invariants of classical and virtual knots[J].Topology,2000,39: 1045-1068.

[3] Itik M,Banks S P.On the calculation of the Kauffman bracket polynomial[J].Applied Mathematics and Computation,2010,216:655-661.

[4] Kauffman L H.State models and the Jones polynomial [J].Topology,1987,26:395-407.

[5] Dye H A,Kauffman L H.Virtual crossing number and the arrow polynomial[J].Journal of Knot Theory and Its Ramifications,2009,18:1335-1357.

[6] Miyazawa X.A multi-variable polynomial invariant for virtual knots and links[J].Journal of Knot Theory and Its Ramifications,2008,17:1311-1326.

Maple Calculation of the Kauffman Bracket Polynomial of Virtual Links

LI Mei-lian1*,DENG Qing-ying2
(1.School of Mathematical Science,Xiamen University,Xiamen 361005,China; 2.School of Mathematics and Computer Science,Longyan University,Longyan 364000,China)

We extend the computational method of the Kauffman bracket polynomial by Itik and Banks from classical links to virtual links.The algorithm uses cyclic permutations to count the number of circles of states obtained by the application of A-tybe or B-type smoothing to each classical crossing and the replacement of each virtual crossing with two arcs that they meet transversally.We show that our algorithm can be implemented easily by computer programs written in the Maple environment.

virtual links;Kauffman bracket polynomials;Maple program

10.6043/j.issn.0438-0479.2015.02.014

O 157.5

A

0438-0479(2015)02-0233-05

2014-07-14 录用日期:2014-10-23

国家自然科学基金(11271307);中央高校基本科研业务费专项(0020 ZK1012)

*通信作者:meilian201@163.com

李美莲,邓青英.虚拟链环的Kauffman尖括号多项式的Maple计算[J].厦门大学学报:自然科学版,2015,54(2): 233-237.

:Li Meilian,Deng Qingying.Maple calculation of the kauffman bracket polynomial of virtual links[J].Journal of Xiamen University:Natural Science,2015,54(2):233-237.(in Chinese)