基于非饱和流固耦合理论的某尾矿坝渗流与稳定性分析
2015-12-24胡井友吴龙梁闫茂林谢建斌
胡井友,吴龙梁,闫茂林,汤 卓,谢建斌
(1.西南交通大学 土木工程学院, 四川 成都 610000; 2.云南大学 城市建设与管理学院, 云南 昆明 650091)
基于非饱和流固耦合理论的某尾矿坝渗流与稳定性分析
胡井友1,吴龙梁2,闫茂林2,汤卓2,谢建斌2
(1.西南交通大学 土木工程学院, 四川 成都 610000; 2.云南大学 城市建设与管理学院, 云南 昆明 650091)
摘要:基于非饱和流固耦合理论,针对某尾矿坝,建立了流固耦合渗流有限元模型,通过对尾矿库的浸润线位置以及应力场分布规律的分析,验证了流固耦合数值模拟的有效性。并在此基础上,采用流固耦合—Morgenstern-Price法,获得了不同干滩面长时尾矿坝的稳定性安全系数,并将其与采用极限平衡法、流固耦合—强度折减法获得的计算结果进行了对比分析。结果表明:采用流固耦合—Morgenstern-Price法研究尾矿坝的稳定性是有效和可靠的。
关键词:流固耦合;渗流分析;强度折减法;极限平衡法;尾矿坝
尾矿库运行不当将会带来严重的环境和灾害问题。当前,国内外发生了大量因尾矿坝失稳而引发的重大灾害事故[1]。尾矿坝已成为严重威胁下游居民生命财产安全的重大危险源,开展尾矿坝稳定性研究工作尤显必要和迫切。尾矿库渗流问题是影响尾矿坝安全稳定性的关键因素[2]。目前,国内外学者针对渗流理论和尾矿坝渗流场分布规律等课题进行了大量的研究,并取得了丰硕成果[2-4]。然而,当前关于尾矿坝渗流问题的研究多数仅基于单纯的流体渗流理论,而忽略了流固耦合作用的影响,只得到了渗流问题的近似解。实际上,流固耦合效应对尾矿库的安全运行影响显著,不容忽视[5-7]。目前,关于尾矿坝稳定性的研究方法大体可归纳为两类,即有限元强度折减法和极限平衡法[8]。极限平衡法求解时,须对浸润线位置以及初始滑裂面做出假设,假设的合理性影响到求解结果的可靠性。强度折减法虽不需事先给定求解条件,但因受失稳判据难以正确选定等因素的影响而不易有效的实现[9-11]。因此,寻求有效且可靠的稳定性分析方法,有待进一步的研究与探讨。
本文针对云南省朵木得尾矿库,进行了流固耦合渗流分析。并在流固耦合渗流分析的基础上,尝试采用流固耦合—Morgenstern-Price法,得到了尾矿坝不同干滩面长度的安全稳定系数,并将计算结果与采用其他方法得到的计算结果进行了对比分析,验证了流固耦合—Morgenstern-Price法在尾矿坝稳定性研究方面的可靠性与适用性。
1流固耦合—Morgenstern-Price法
1.1 流固耦合理论
鉴于库内部分尾矿料处于非饱和状态,本文采用文献[7]提出的饱和-非饱和流固耦合理论。
其中,饱和-非饱和渗流有限元微分方程可表述为:
[K]{H}-[M]{H},t=0
(1)
式中:[M]=∫A(C{N}T{N})dA;[K]=∫A([B]T[K][B])dA
非饱和材料饱和度或体积含水率与基质吸力的函数关系可用如下方程表述:
Pnw-Pw=F(Sr,n,Sr0,n0)
(2)
式中:Sr为饱和度;Pw为孔隙水压力;Pnw为孔隙气压力;n为孔隙率;Sr0为体积含水率。
达西定律结合质量守恒方程可得到平衡微分方程:

(3)
式中:ρw为水的密度;Z为位置水头;Kw为水的渗透系数;其他符号—数值参数。
考虑孔隙水压力时,可推求应力场-渗流场耦合平衡方程:
div(D·ε(u))-χgrad(Pw)-(1-χ)grad(Pnw)+γ=0
(4)
式中:D为刚度矩阵;u为位移;χ为非饱和土参数;γ为密度。
1.2 极限平衡原理
极限平衡方程由两个安全系数方程组成,即力矩平衡安全系数方程与静力平衡安全系数方程[8]。其中,力矩平衡安全系数方程为:
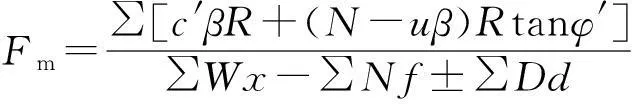
(5)
水平方向静力平衡安全系数方程为:

(6)
式中:c′为有效黏聚力;φ′为有效摩擦角;u为孔隙水压力;N为土条底部法向力;W为土条重量;D为集中荷载;β,R,f,d,ω为几何参数;α为土条地面倾角。
1965年Morgenstern和Price共同研究出了一种同时满足力矩平衡和力的平衡的土坡稳定性分析方法—Morgenstern-Price法,简称M-P法。与其他极限平衡法不同的是,M-P法考虑了多种形式的条间力函数。M-P法条间剪切力由如下式表述[8]:
X=Eλf(x)
(7)
式中:x为表示函数;E为条间法向力;λ为函数所用的百分数;f(x)表示函数。
2工程实例
朵木得尾矿库位于云南省富民县,距昆明市23km。地势南高北低,河谷和盆地面积占总面积的12.5%。尾矿坝初期坝最大坝高25m,坝底高程为1 760m,坝顶高程为1 785m,坝体内外坡比均为1∶1.75。堆积坝采用上游法堆积,终期堆积坝高程为95m,终期堆积坝顶高程为1 855m,终期堆积坝体内总坡比为1∶100。岩土种类较多且均匀性较差,尾矿库相关的材料数值计算参数如表1所示。
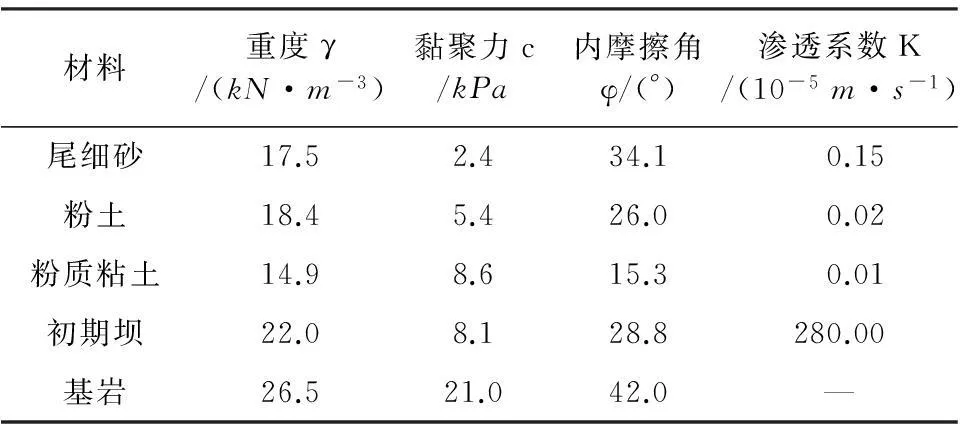
表1 尾矿库材料数值计算参数
3有限元数值模拟
将尾矿库剖面进行合理概化,采用Geo-Slope有限元分析软件建立流固耦合渗流有限元模型(图1)。

将尾矿料视为等效连续多孔介质材料,基于非饱和流固耦合原理,根据材料的级配数据,采用文献[12]建议的间接法估算初期坝和尾细砂的土水特征曲线(图2、图3),并利用VanGenachten拟合法推求渗透系数(图4、图5),从而计算得到渗透压力。将渗透压力与应力场进行叠加,使应力场得到更新,以完成一次耦合分析的循环,从而实现流固耦合渗流分析。在流固耦合渗流分析的基础上,采用Mohr-Coulomb弹塑性本构模型,进行尾矿坝稳定性分析。

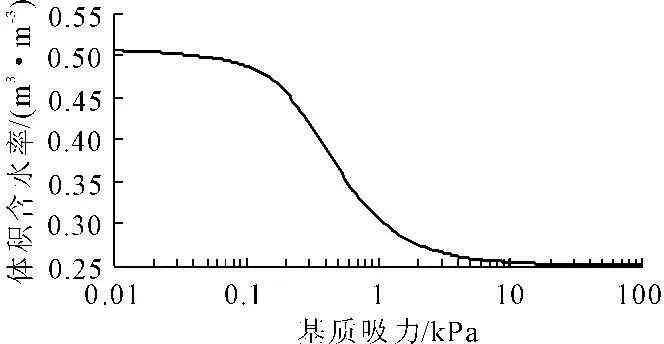
图2 初期坝土水特征曲线

图3 尾细砂土水特征曲线
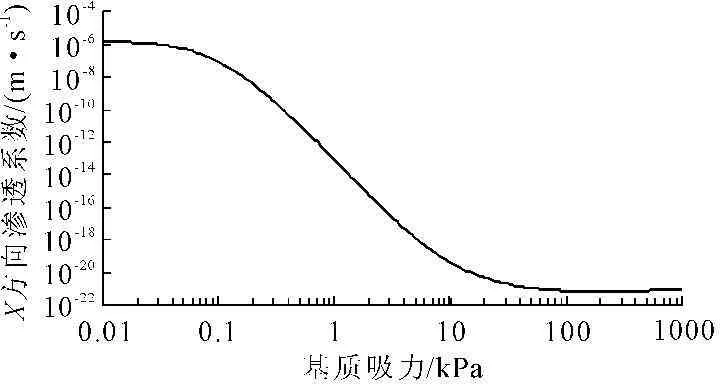
图4 初期坝渗透性函数
图5尾细砂渗透性函数
4计算结果及分析
利用Geo-Slope有限元软件中自带的Seep/W、Sigam/W模块进行耦合计算,从而实现了流固耦合效应的数值模拟,得到了尾矿坝在正常工况下尾矿库的浸润线及应力场的分布规律,为极限平衡法以及强度折减法的求解提供基础。计算结果如图6~图9所示。


图6 非流固耦合浸润线位置
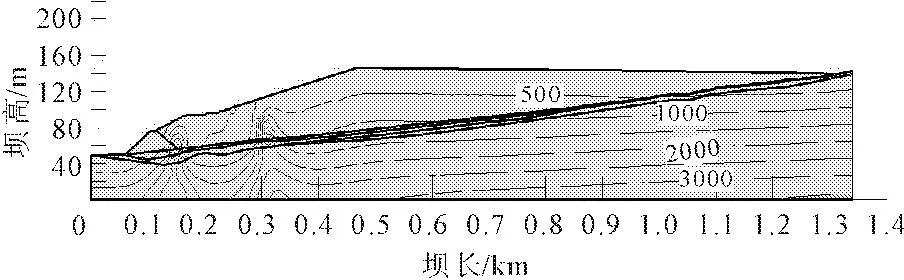
图7 流固耦合浸润线位置

图8 非流固耦合竖向应力(单位:kPa)
图9流固耦合竖向应力(单位:kPa)
由图6、图7可知,耦合计算浸润线埋深明显小于非耦合计算浸润线埋深。且耦合计算结果与实测数据吻合较好,验证了流固耦合数值模拟的有效性。由图8、图9可知,耦合计算竖向应力较非耦合计算竖向应力略有增大,应力扩大现象在基岩应力集中处表现更为明显。分析原因可知,考虑流固耦合效应时,一方面由于土(岩)体内地下水动水压力作用于土(岩)体骨架,改变了原有土体颗粒结构的排列[13]。当土体细微颗粒骨架受孔隙水压力挤压发生变形时,土(岩)体内部发生应力重分布。另一方面,由于土体细微颗粒骨架变形改变了水的运移路径,导致了水的渗透率变化,从而影响了土(岩)体内部的渗流状态[13]。本算例表现为尾矿库内应力受渗流的影响而增大。与此同时,应力场的改变反向影响了渗流,从而提高了浸润线的位置。
利用Geo-Slope有限元软件中自带的Slope/W模块,采用Mohr-Coulomb弹塑性本构模型,进行尾矿坝稳定性分析。分别利用流固耦合—Morgenstern-Price法、Morgenstern-Price法、流固耦合—强度折减法计算尾矿坝不同干滩面长度时的抗滑稳定性安全系数,计算结果如图10所示。其中,流固耦合—强度折减法的可靠性已得到了充分验证[5-7]。鉴于Mohr-Coulomb破坏准则考虑了黏聚力以及内摩擦角对土体屈服的影响,能够较好的反映工程实际。本文针对尾矿料的材料特性以及尾矿坝的实际情况,选用Mohr-Coulomb破坏准则作为强度折减法判断失稳的依据。
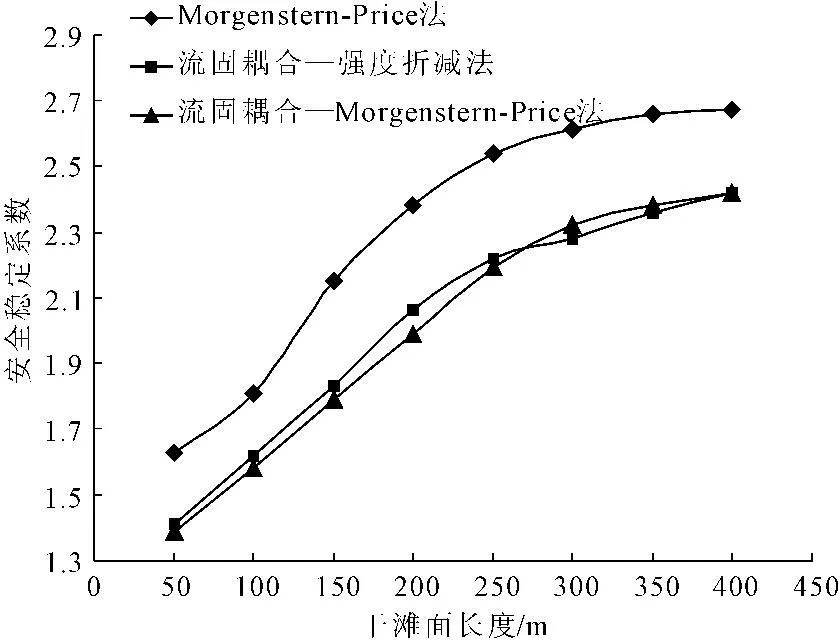
图10安全系数计算结果
分析图10中的数据可知,流固耦合—Morgenstern-Price法与流固耦合—强度折减法计算结果对比,最大相对误差为3.5%,证明了流固耦合—Morgenstern-Price法的可靠性。流固耦合—Morgenstern-Price法与Morgenstern-Price法计算结果对比,最大相对误差为17.8%,说明了流固耦合效应对稳定性计算结果影响显著。且Morgenstern-Price法的计算结果较可靠值偏大,而使得对尾矿库的安全稳定性评估偏高,不利于尾矿库的安全生产与控制。
实际上,能够考虑到各种重要的影响因素,并将其融合为一个整体体系进行耦合分析的方法才是最为理想的抗滑稳定性分析方法。而流固耦合—Morgenstern-Price法恰是一种将渗流分析、应力应变分析以及稳定性分析进行耦合分析与计算的方法。一方面,流固耦合—Morgenstern-Price法能够给定更准确的浸润线位置,并且可根据所求得的应力场分布规律假定更为合理的初始滑裂面位置以及形状。计算结果相比极限平衡分析法更为准确与可靠。另外一方面,流固耦合—Morgenstern-Price法不仅可得到与流固耦合—强度折减法同样可靠的求解结果,并且克服了强度折减法失稳判据选择困难等因素影响的问题,原理相对简明清晰。因此,流固耦合—Morgenstern-Price法是一种可行且有效的稳定性分析方法。
5结论
(1) 流固耦合渗流分析得到的浸润线位置与工程实际更为接近,比非流固耦合渗流分析得到的浸润线位置高25%左右。
(2) 流固耦合效应主要是通过影响尾矿库的渗流从而影响尾矿坝稳定性的,且对尾矿坝渗流与稳定性分析影响显著。
(3) 流固耦合—Morgenstern-Price法与流固耦合—强度折减法的计算结果相近,是一种可靠的分析方法,可应用于尾矿库抗滑稳定性分析。
参考文献:
[1]柴建设,王姝,门永生.尾矿库事故案例分析与事故预测[M].北京:化学工业出版社,2011.
[2]速宝玉,詹美礼,郭振世,等.金堆城栗西尾矿坝三维渗流控制研究[R].南京:河海大学,2006.
[3]XieJianbin,FanJing,WangZhiliang,etal.Numericalsimulationonthethree-dimensionalseepagefieldofZhelamuqingtailingsdam[J].AppliedMechanicsandMaterials, 2013,256-259:19-25.
[4]路美丽,崔莉.复杂地形尾矿坝的三维渗流分析[J].岩土力学,2006,27(7):1176-1180.
[5]韩建波,张力霆,李强,等.流固耦合—强度折减法在尾矿坝稳定性分析中的应用[J].金属矿山,2011(11):29-32.
[6]张延军,王恩志,王思敬.非饱和土中的流—固耦合研究[J].岩土力学,2004,25(6):999-1004.
[7]李强,张力霆,齐清兰,等.基于流固耦合理论某尾矿坝失稳特性及稳定性分析[J].岩土力学,2012,33(S2):243-250.
[8]邵龙潭,李红军.土工结构稳定分析—有限元极限平衡法及其应用[M].北京:科学出版社,2011.
[9]迟世春,关立军.应用强度折减有限元法分析土坡稳定的适应性[J].哈尔滨工业大学学报,2005(9):1298-1302.
[10]李红,宫必宁,陈琰.有限元强度折减法边坡失稳判据[J].水利与建筑工程学报,2007,5(1):79-82.
[11]郑文棠.基于FLAC3D的强度折减法和点安全系数法对比[J].水利与建筑工程学报,2010,8(4):54-57.
[12]刘建立,徐绍辉,刘慧.估计土壤水分特征曲线的间接方法研究进展[J].水利学报,2004,35(2):68-78.
[13]周维垣.高等岩石力学[M].北京:水利电力出版社,1990.
DOI:10.3969/j.issn.1672-1144.2015.04.025
收稿日期:2015-01-29修稿日期:2015-03-09
基金项目:国家自然科学基金资助项目(51264037);云南省应用基础研究计划面上项目(2011FB010)
作者简介:胡井友(1978—),男,四川遂宁人,高级工程师,主要从事流固耦合理论研究及其在尾矿坝中的应用。E-mail:ramlee@126.com 通信作者:谢建斌(1973—),男,浙江台州人,教授,主要从事岩土工程、防灾减灾工程研究。E-mail:377315928@qq.com
中图分类号:TV3
文献标识码:A
文章编号:1672—1144(2015)04—0126—04
Seepage and Stability Analysis of A Tailings Dam Based on Unsaturated Fluid-solid Coupling Theory
HU Jingyou1, WU Longliang2, YAN Maolin2, TANG Zhuo2, XIE Jianbin3
(1.SchoolofCivilEngineering,SouthwestJiaotongUniversity,Chengdu,Sichuan610000,China;2.SchoolofUrbanConstructionandManagement,YunnanUniversity,Kunming,Yunnan650091,China)
Abstract:Based on unsaturated fluid-solid coupling theory, a finite element model of fluid-solid coupling seepage was established. The effectiveness of the numerical simulation by this model was testified through the analysis of the location of the infiltration line and the distribution law of the water pressure. Further more, the safety index of the dam’s stability under the conditions of different dry beach lengths was obtained by using fluid-solid coupling-Morgenstern-Price method, and then compared with the caculation results of limit equilibrium method and fluid-solid coupling-strength reduction method. The comparsion results indicate that fluid-solid coupling-Morgenstern-Price method is effective and reliable in the application of stability research of tailings dams.
Keywords:fluid-solid coupling; seepage analysis; strength reduction method; limit equilibrium method; tailings dam
