基于蒙特卡罗法的挑流消能风险分析
2015-12-24尤嘉惠王长新
尤嘉惠,王长新
(1.乌鲁木齐水业建设投资有限公司, 新疆 乌鲁木齐 830049;2.新疆农业大学 水利与土木工程学院, 新疆 乌鲁木齐 830052)
基于蒙特卡罗法的挑流消能风险分析
尤嘉惠1,王长新2
(1.乌鲁木齐水业建设投资有限公司, 新疆 乌鲁木齐 830049;2.新疆农业大学 水利与土木工程学院, 新疆 乌鲁木齐 830052)
摘要:在现今实际的挑流工程中,既要保证挑流消能的局部冲刷不会影响坝身安全和岸坡稳定,同时又要求更经济的造价。为了在安全与经济之间取得平衡,综合考虑洪峰流量和洪水过程的不确定性,用蒙特卡罗方法对挑流消能进行了风险率计算,并分析了下泄流量、冲坑系数、洪峰消减系数等不确定性因素对风险的影响。结果表明在考虑洪水不确定性时,挑流消能的风险有所减小,下泄流量、冲坑系数和洪水过程不确定性对挑流消能风险的影响比较显著。
关键词:挑流消能;风险率;Matlab;蒙特卡罗;随机数
挑流消能是工程泄水消能方式中常见的衔接消能方式,泄水建筑物在下泄洪水时,势能转化成动能,水舌在鼻坎挑出过程中消耗的能量一般不超过10%~20%[1],下游河床承受绝大多数的能量。因此,挑流消能要求下游河床基岩要有较高的抗冲能力,使下游的局部冲刷不会危及坝身安全和岸坡稳定。一般要求挑流挑距应不小于最大冲坑深度的3~4倍,这样才能保证工程的安全[2]。但为了节省工程投资,还有工程布置的要求,建筑物需要尽可能减小泄流宽度,以至于增加了单宽流量。为了工程在安全与经济之间取得平衡,本文运用蒙特卡罗法对挑流消能进行风险分析。
1影响挑流消能风险的不确定性因素
挑流消能系统中影响挑流局部冲刷的因素较多,诸如:工程布置、下泄流量、挑坎尺寸、冲坑后下游水深、地质条件和运行情况等,这些因素都具有不确定性。
正因为存在着这些不确定性因素,风险才会产生。我们将挑流消能的风险不确定性大致分为以下两种:水文不确定性、水力不确定性[3]。
1.1 水文不确定性
1.1.1洪峰流量不确定性[4]
由于自然因素(地貌、气温、暴雨时间和区域等)的随机性引起洪峰流量的不确定性,使得天然河道的实际来流量及水位超过设计值[5]。
洪峰流量的不确定性在挑流消能风险的分析计算中是相当重要的。根据资料,我国最大洪峰流量服从的是P-Ⅲ型分布[3]。其概率密度函数为:
(1)
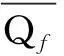
1.1.2洪水过程不确定性
在进行挑流消能风险分析与计算时,洪水过程不确定性对它是有影响的,所以必须要考虑到。这是因为:实际发生的洪水过程与进行设计时调洪演算后得到的洪水过程不可能完全一致,这就使洪水在调洪后所得的最大下泄流量以及最高水位与设计值不一致。为了描述水库调洪的作用,我们引入洪峰消减系数η这个概念:
(2)
式中:Q0为经过水库调蓄作用后能够下泄的最大出库流量;Qf为河道中洪水的洪峰流量。
1.2 水力不确定性
1.2.1过流结构不确定性
在工程施工过程中,由于各个方面的原因,如施工技术、工艺、施工人员以及工程管理等,使得建筑物的实际过流结构尺寸与设计时的过流结构尺寸存在一定的误差,从而工程实际的下泄流量也与设计下泄量不一致。这在工程上是允许的。根据误差理论,对于过流结构尺寸的不确定性进行研究,认为结构尺寸是服从正态分布,将其设计值作为均值,而标准差按下式进行估算[7]:
σ=1.25θ
(3)
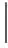
(4)
1.2.2水位不确定性
由于洪峰流量具有不确定性,洪水过程及工程运行情况也具有不确定性,这就导致了水位不确定性的产生。

(5)
1.2.3水力计算模型的不确定性
在对泄水建筑物进行设计时所运用到的水力学方面计算公式也存在不确定性,可通过一个不确定性系数λ来表示,规定其均值为1,可适当的酌情选择其标准差。
在用到的水力学计算公式中,选取相关变量及各种参数时也存在着不确定性,如:流速系数及糙率等。由中心极限定理可知,可以将这些参数当作是服从正态分布的,其设计值定为均值,在可变范围内根据式(3)和式(4)来估算其标准差[8]。
2挑流消能风险计算模式
综合以上各不确定性因素,本文主要从挑流消能冲刷坑对挑流(泄水)建筑物影响的角度来分析计算挑流消能的风险。
将挑流消能的风险定义为:在正常运行情况下,挑坎末端至冲刷坑最深点的平均坡度大于最大临界坡度的概率。计算模式为
R=P(ik (6) 用极限状态方程表示为 Z*=ik-i (7) ts=Kq0.5Z0.25-ht (8) 式中:K为冲坑系数;q为下泄单宽流量;Z为上下游水位差;ht为下游水深。 (9) (10) 式中:T为冲刷坑深度(从下游水位起算的),T=Kq0.5Z0.25;β为挑流射出水舌的外缘与下游水面间的夹角; (11) 将以上的各因素带入功能函数,即: (12) 3蒙特卡罗法(Monte Carlo Method法) 蒙特卡罗法是从目标函数对应的分布中,人为的生成一个含有特殊随机变量的系列,然后对其进行模拟与计算,最终的风险是对得到的计算结果通过检验估算出来的[11]。具体步骤如下: 利用伪随机数生成的方法,抽样生成一组随机数样本值,然后将其转化为服从各变量概率分布的随机数组,再将其代入到极限状态方程(Z*=R-S)中,得到大量的Z*值,统计Z*值小于0的次数,最后小于0的次数与总抽样次数的比被当作该系统的风险值。 (2) 根据Qf所属的分布,代入相应数据,生成Qf的随机数(用舍选法); (3) 模拟生成挑流消能计算中不确定因素(Qf、η、K、a、B、R、θ)的随机数; (4) 根据水力学公式,计算出平均坡度i,即冲刷坑深度与挑流射程的比值; (5) 将(4)中求得的最大临界坡度ik与平均坡度i相减,得到Z值。若Z大于0,则失效次数N=N+1,重复步骤(3)至(5),当N等于M时结束重复; Matlab软件其自身配备一些随机数的发生器,它能够直接产生服从某些特定分布的随机数,如均匀分布、正态分布等[8]。但是,与本文计算相关的P-Ⅲ型分布和极值Ⅰ型分布,在软件中没有能直接产生其随机数的发生器。 (1) P-Ⅲ型分布 前文已经说明,洪峰流量Qf服从的是P-Ⅲ型分布,其对应的概率密度函数已知。根据舍选抽样法[13-14],并利用Matlab软件编制相关程序来产生该不确定性因素的随机数。 (2) 极值Ⅰ型分布 求解极值Ⅰ型分布时,必须首先对x=F-1(r)进行求解,则服从该分布的随机数x即可得到。文献[15]已经提供了产生该分布随机数的相关公式。如下: xi=μx-0.45σx-0.7797σxln(-lnui) (13) 式中:ui为服从均匀分布的随机数;xi为服从该极值Ⅰ型分布的随机数。 本文计算中所涉及到的洪峰消减系数η经过假设检验后,认为服从极值Ⅰ型分布。 4算例 一水利工程主要由挡水建筑物大坝、泄水建筑物溢流坝及底孔组成。溢流坝段位于原河槽部位,两侧为非溢流坝段。设计洪水重现期为500 a一遇,相应洪峰流量为4 318.75 m3/s,校核洪水重现期为5 000 a一遇,相应洪峰流量为5 640.64 m3/s。从水文站给出的实测资料中可以看出,最大的洪峰流量为Q=3 040 m3/s。通过对历史洪水资料进行频率分析,得到的洪水特征参数及频率结果见表1。经过调洪验算后的成果表见表2。 表1 洪水洪峰流量统计特征参数及频率 表2 调洪计算成果表 重力坝高140.33 m,泄流段总长约为116 m,堰顶高程为594 m。溢流段采用鼻坎挑流消能,鼻坎高程494 m,反弧半径17.3 m,挑角33°。 (1) 建立极限状态方程:Z=ik-i(Qf、η、K、a、B、R、θ),其中7个不确定性因素的取值见表3。 表3 各随机变量取值表 (13) (2) 分别产生服从P-Ⅲ型分布的下泄流量Qf的随机数,服从极值Ⅰ型分布的洪峰消减系数η的随机数,服从正态分布的挑坎尺寸(坎高a、坎宽B、反弧半径R、挑角θ)和冲坑系数K的随机数,将以上随机数代入到极限状态方程中,最后统计ik 表4 风险计算成果表 (4) 对比考虑洪水过程不确定性因素与否对风险的影响,见表5。 表5 洪水过程不确定性对风险的影响对比表 表6 灵敏度分析表 图1 各不确定性因素对风险的影响(100000次) 图2各不确定性因素对风险的影响(1000000次) (1) 由表4可知,考虑了洪峰流量和洪水过程不确定性后,挑流建筑物风险率平均为0.00214。 (2) 由表4可知,挑流消能的风险随着模拟次数的改变而变化。模拟次数由1万次逐渐增加到1000万次时,挑流风险值是逐渐向实际风险值趋近的,但是实际值现阶段还是未知的,这就需要今后对此进行大量的实验或分析大量的样本来得到。 (3) 由表5可知,考虑洪水过程不确定性时的风险小于不考虑它时的风险,风险减小了33.75%。由此可知,在分析计算挑流消能风险时,有必要考虑洪水过程(洪峰消减系数η)的不确定性。 (4) 由表6、图1及图2可知,下泄流量Qf(风险率平均为0.00204)、洪峰消减系数η(风险率平均为0.001915)和冲坑系数K(风险率平均为0.00145)相对来说,对挑流风险的影响较大;挑坎尺寸(坎高、坎宽、反弧半径、挑角)对挑流风险影响较小。 (5) 通过Matlab软件计算风险,模拟次数为1000万时,耗时为1 179 s,提高了蒙特卡罗方法的效率。 5结论 (1) 用蒙特卡罗法计算挑流风险率的关键是产生服从已知分布的随机数,这项工作的计算量是庞大的,而通过Matlab软件能快速得到,解决了这一问题。 (2) 通过灵敏度分析可知,下泄流量、洪峰消减系数和冲坑系数对挑流风险的影响较大。 (3) 本文利用Matlab软件进行编程,成功解决了软件不能直接生成P-Ⅲ型分布及极值Ⅰ型分布的随机数的这一问题。 (4) Matlab软件直接运算矩阵的功能,能够使编程不再用非常繁琐的If语句,从而使编程工作得到大大的简化,提高了效率。 (5) 本文只是利用Matlab软件计算了挑流风险率,对于挑流如何优化和系数的选取等问题还需要研究。 参考文献: [1]李亮.基于混凝土大坝的泄洪建筑物风险指标体系及泄洪风险研究[D].西安:西安理工大学,2007. [2]徐祖信,郭子中.二滩大坝表孔跌流中孔挑流的冲刷风险分析[J].水动力学研究与进展,1990,5(3):102-109. [3]徐祖信,郭子中.混凝土高坝泄洪可靠度研究[J].河海大学学报,1990,18(2):76-82. [4]王长新.施工导流风险分析与计算[J].八一农学院学报,1994,12(17):11-15. [5]陈凤兰,王长新.施工导流风险分析与计算[J].水科学进展,1996,7(4):361-366. [6]赵经华.泄洪风险计算软件包的研究及其在工程风险计算中的应用[D].乌鲁木齐:新疆农业大学,2005. [7]杨惠莲,张涛.误差理论与数据处理[M].天津:天津大学出版社,1992. [8]张虎.新疆某水利枢纽工程施工导流风险分析和导流方案多目标决策[D].乌鲁木齐:新疆农业大学,2013. [9]邱秀云.水力学[M].乌鲁木齐:新疆电子出版社,2004. [10]李炜.水力计算手册[M].北京:中国水利水电出版社,2006. [11]吴世伟.结构可靠度[M].北京:人民交通出版社,1990. [12]王丽学,林凤伟,汪可欣,等.基于蒙特卡洛模拟的泄洪风险率计算[J].人民长江,2008,39(19):20-22. [13]丛树铮.水文学的概率统计基础[M].北京:水利出版社,1981. [14]王长新,王惠民,徐祖信,等.泄洪风险计算方法的比较[J].水力发电,1996,12(1):13-16. [15]吕满英.考虑洪水过程不确定性的泄洪风险分析[D].乌鲁木齐:新疆农业大学,2002. DOI:10.3969/j.issn.1672-1144.2015.04.029 收稿日期:2015-03-01修稿日期:2015-04-18 作者简介:尤嘉惠(1990—),女,河南项城人,硕士,研究方向为水力可靠度理论。E-mail:873560879@qq.com 通讯作者:王长新(1957—),男,辽宁抚顺人,教授,博士生导师,主要从事水工水力学、河流泥沙和水力可靠度理论方面的研究和教学工作。E-mail: 420273169@qq.com 中图分类号:TV135.2+3 文献标识码: A 文章编号: 1672—1144(2015)04—0146—05 The Risk Analysis of the Trajectory Energy Dissipation Based on Monte Carlo Method YOU Jiahui1, WANG Changxin2 (1.UrumqiWaterIndustryConstructionInvestmentCo.,Ltd.,Urumqi,Xinjiang830049,China;2.CollegeofHydraulicandCivilEngineering,XinjiangAgriculturalUniversity,Urumqi,Xinjiang830052,China) Abstract:In actual hydraulic projects, it is required that the local scour of the trajectory energy dissipation should not affect the safety of the dam body and the stability of the slope, meanwhile a satisfactory low cost should be upheld. In order to achieve the balance between safety and economy, the risk of the trajectory energy dissipation was calculated using Monte Carlo method, with the consideration of the uncertainties of flood peak discharge and flood process. And then the effects of uncertainty factors on the risk of trajectory energy dissipation were analyzed, such as the discharge, the scour coefficient, the peak attenuation coefficient and etc. The results showed that the risk decreased when the flood process uncertainty was in consideration and the discharge, the scour coefficient and the flood process uncertainty significantly influenced the risk of the trajectory energy dissipation. Keywords:trajectory energy dissipation; risk rate; Matlab; Monte Carlo method; random number2.1 冲刷坑深度ts[10]
2.2 挑流鼻坎至下游水面间的挑流距离,即空中挑距L0
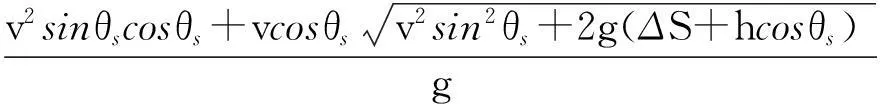
2.3 水下射程(水面以下水舌长度水平投影)L1

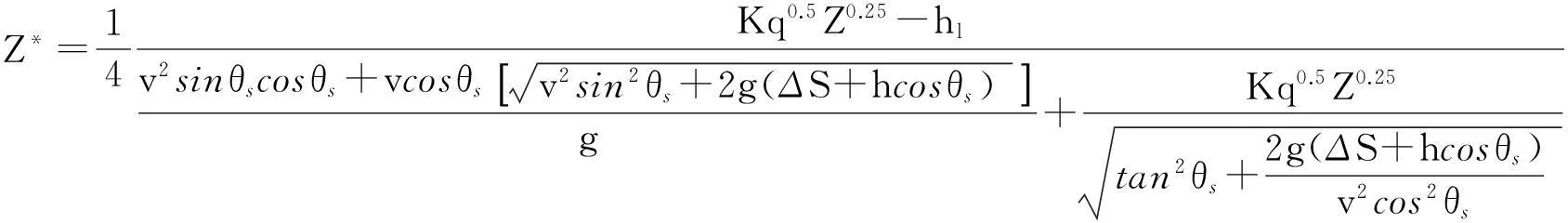
3.1 计算步骤[12]
3.2 随机数抽样
3.3 P-Ⅲ型分布与极值Ⅰ型分布的随机数抽样
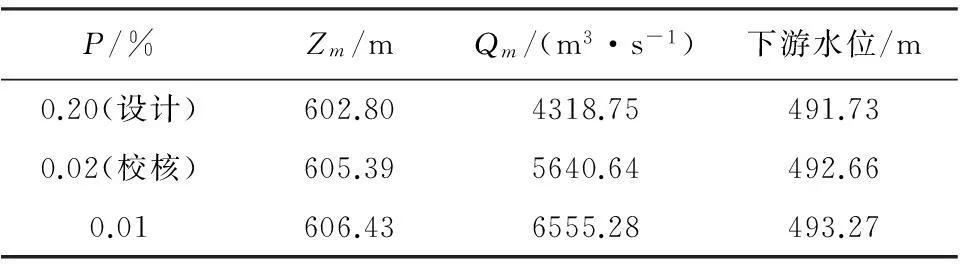
4.1 工程概况

4.2 挑流风险计算





4.3 灵敏度分析


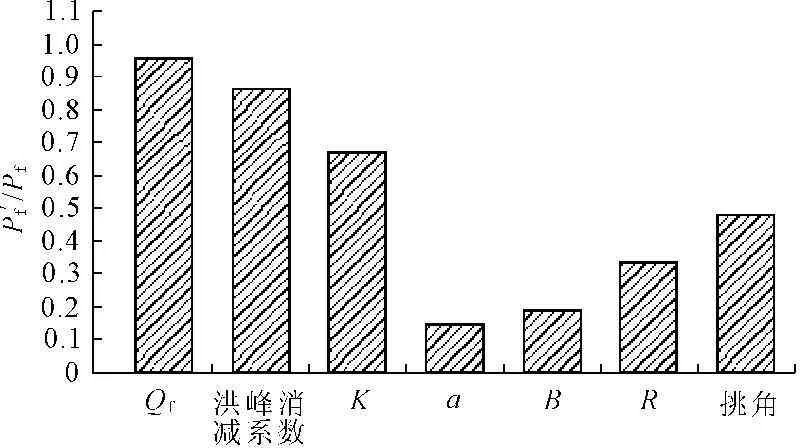

4.4 计算结果
