热膨胀过程中流固耦合应力分析的等效方法

王泽宝+赵鹏+冯能莲+丁能根

摘要： 密闭容器内的液体受热膨胀后，会挤压容器并使其受力变形直至破裂，而传统的流固耦合分析方法难以解决这种流固耦合场、应力场和温度场等多场耦合的问题.利用等效表面载荷的方法来模拟膨胀的液体与固体之间的相互作用，可分析在温度升高过程中内部充满液体的某个容器的受力情况.通过本方法对容器进行动态应力分析，可等效得到容器某个部分结构失效时，容器内壁所受载荷的具体大小及其容积的变化，并可对应得到某处结构失效时刻的准确温度.该方法可有效解决多场耦合的问题，并且省去液体模型，提高分析和计算速度.结合电池冷却箱受热膨胀的算例进一步阐释该方法.

关键词： 密闭容器； 热膨胀； 结构失效； 应力； 流固耦合； 多场耦合； 等效方法

中图分类号： TB115文献标志码： B

Abstract： While the liquid in an airtight container is being heated， the container will be deformed and even fractured. It can hardly be solved by traditional fluidsolid coupling analysis method， because it is a multifield coupling problem， which includes fluidsolid coupling field， stress field， temperature field， and so on. A method of equivalent surface load is proposed to simulate the fluidsolid interaction in the process of thermal expansion， which can be used for stress analysis on the force of a container filled with liquid in the process of temperature increase. With the dynamic stress analysis of the container using the method， the specific load on the container inner wall and the volume change can be obtained when the structural failure appears， and the accurate temperature of the failure part at the failure time can be obtained. The method can effectively solve the multifield coupling problem， and the speed of analysis and calculation can be improved while the liquid model is omitted. The method is further explained by the thermal expansion example of a battery cooling tank.

Key words： airtight container； thermal expansion； structural failure； stress； fluidsolid coupling； multifield coupling； equivalent method

0引言

若密闭固体容器内充满某种液体，当温度升高时，由于液体受热膨胀明显比固体要大，所以液体会挤压容器内壁，造成其变形甚至破裂.为确认容器破裂时的准确温度，应对固体容器进行多场分析，包括流固耦合场、应力场和温度场等的分析，但是传统的流固耦合方法难以完成多场分析[1].同时，某些容器内表面构型比较复杂，若对液体模型划分网格，计算量过大.为解决这些问题，考虑省去液体模型，通过在容器内表面施加均匀压力模拟液体与容器之间的作用，在有限元软件中提取容器变形前与变形后的节点坐标，借用ImageWare将节点拟合成闭合的曲面[2]，并在SolidWorks中由闭合曲面构成实体后得到其体积[3]，此体积即为等效液体的体积，利用液体温度、压强和体积之间的关系即PTV特性，对应得到此时等效液体的温度.

1液体等效方法

连通的液体在同一高度的压强处处相等.因为大部分容器内液体高度差较小，在液体热膨胀过程中，抵抗容器内壁压缩的压力远大于因高度差造成的压力，所以可以假设温度升高过程中液体对容器内壁作用的压力处处相等.在其弹性变形内，容器内表面受力大小决定容器变形大小，因此可将液体模型省去，通过在容器内表面施加均匀压力模拟液体与容器之间的作用，并通过逐步加大压力来模拟液体受热膨胀过程中对容器内表面的挤压过程.

2等效液体的PVT特性

2.1液体的体积模量

假设在压强P0作用下，一定量液体的体积为V0，当压强变化为dp时的体积变化量为dv，则液体的体积模量[4]K=-dPd（V/V0） （1）普通液体的体积模量在不同温度、不同壓力下变化不大，可视为固定值.大部分液体的体积模量可查，比如水的体积模量为2.18 GPa左右；若需得到某种特定液体的体积模量，可用迈克尔逊干涉仪等方式进行测量.[5]

2.2冷却液体积与温度和压强的关系

随着温度的升高，液体的密度减小，常用液体的密度表可查阅相关手册[6]，而特定液体不同温度下的密度（不考虑相变）可用密度仪测得[7].在一定压强作用下，假设液体20 ℃时体积为V0，密度为ρ0，若温度增加到T时，液体的密度为ρT，在液体所受压强不变的情况下，可知此时冷却液的体积只与温度有关，即VT=V0×ρ0ρT （2）假设温度T下液体所受压强增加P，根据体积模量K的定义可知，此时冷却液体积会相对缩小，缩小的体积占原总体积的P/K，因此，此时冷却液体积V（T，P）=V0×ρ0ρT×1-PK （3）密闭容器内的液体在受热膨胀挤压容器内壁的过程中，当温度T升高时，液体作用于壳体的压强P随之增加.同时，容器内腔的体积也逐渐增大.假设温度升高到T1后变形达到平衡时的液体压强为P1，冷却液体积变为V1，根据式（1）可得此时冷却液体积V1与压强P1和温度T1之间的关系为V1=V0×ρ0ρT1×1-P1K （4）在等效方法中，已知液体的体积模量K与初始温度下液体的密度ρ0，在容器内壁施加垂直于内壁表面且处处相等的压力P1之后，根据变形前的节点坐标和变形后的节点坐标，在ImageWare软件中分别构造变形前和变形后的封闭曲面，并导入到SolidWorks中生成实体模型，计算变形前和变形后的体积V0与V1，可以得到在温度变化之后等效液体的密度ρT，查看液体不同温度下的密度表，可得到此时等效液体的温度T1.

3算例及结果

以某电动车电池冷却箱冷却液的热膨胀受力过程为例进行实例计算.冷却箱的进、出液口因火焰或其他外部环境影响而堵塞，整个冷却箱成为一个密闭的容器，冷却液充满在整个冷却箱中.利用本文的等效方法求解箱体某个部位结构失效时的准确温度.

整个电池箱分为上下盖板和侧围板，其中在下盖板上开有V型槽，使得箱体更容易在下方破裂.冷却箱的计算模型见图1.冷却液为50%乙二醇水溶液，其密度表[8]见表1.整个箱体为6061T4铝合金材料，其主要材料属性[9]见表2.对冷却箱侧围板与车架固连的6个位置对应的节点施加全约束，在冷却箱内表面依次施加0.2，0.4，0.6，0.8和1.0 MPa的压强，有限元模型求解完成后分别提取各载荷步下冷却箱模型内表面上所有节点的位移并与变形前相应节点坐标叠加[10]，通过ImageWare将节点逆向拟合为曲面，导入SolidWorks中生成实体模型并计算内表面围成的体积，可以得到等效冷却液的体积，见表3.

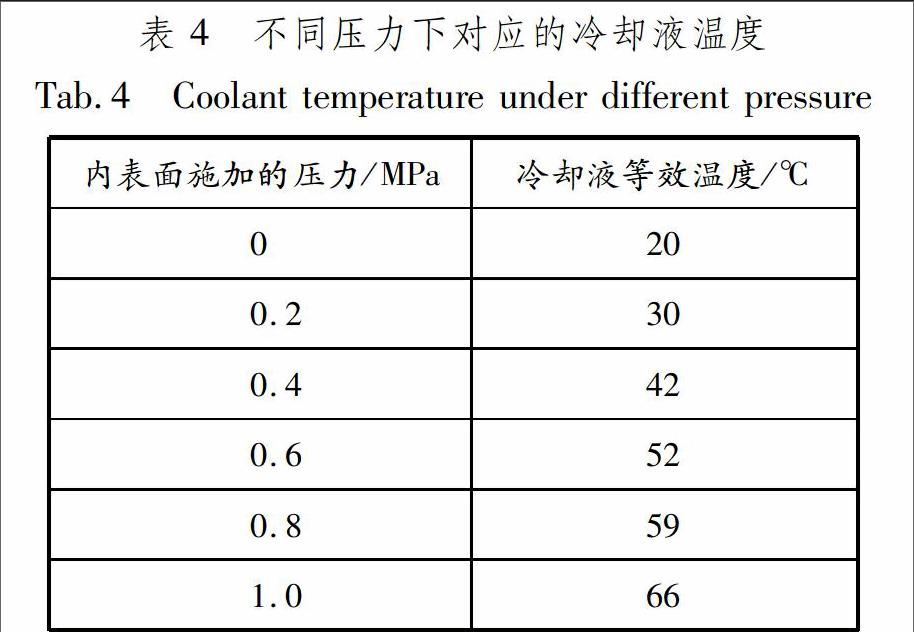
按照式（4），通过计算和查表得到不同冷却液压力下的冷却液等效温度，见表4.与材料的最大许用应力进行对比，经过分析发现整个冷却箱最大应力出现在V型槽处，且当内表面施加的压力为0.85 MPa时，V型槽处的应力达到材料的屈服强度.对应表4可知，在等效冷却液温度升高到大约61 ℃时，冷却箱会发生结构失效.

4结束语

针对热膨胀过程中的流固耦合应力分析，提出一种等效分析方法.该方法采用等效液体模型，省去液体建模及其网格划分的工作，使有限元分析工作量减少，提高分析与计算速度；综合考虑流固耦合场、应力场和温度场，可有效解决热膨胀过程中的流固耦合应力分析问题.参考文献：

[1]宋学官， 蔡林， 张华. ANSYS流固耦合分析与工程实例[M]. 北京： 中国水利水电出版社， 2012： 113.

[2]单岩， 李兆飞， 彭伟. ImageWare逆向造型基础教程[M]. 2版. 北京： 清华大学出版社， 2013： 5094.

[3]辛文彤， 李志尊. SolidWorks 2012中文版从入门到精通[M]. 北京： 人民邮电出版社， 2012： 5458.

[4]林建忠， 阮晓东， 陈邦， 等. 流体力学[M]. 2版. 北京： 清华大学出版社， 2013： 1089.

[5]张凤兰， 计新. 液体的体积弹性模量测定[J]. 延边大学学报（自然科学版）， 2002， 28（3）： 168170. DOI： 10.3969/j.issn.10044353.2002.03.004.

ZHANG F L， JI X. Measurement of liquid bulk modulus of elasticity[J]. Journal of Yanbian University（Natural Science）， 2002， 28（3）： 168170. DOI： 10.3969/j.issn.10044353.2002.03.004.

[6]張向宇. 实用化学手册[M]. 2版. 北京： 国防工业出版社， 2011： 743782.

[7]实验室振动式液体密度仪： JJG 1058—2010[S].

[8]程能林. 溶剂手册[M]. 5版. 北京： 化学工业出版社， 2015： 230280.

[9]一般工业用铝及铝合金板、带材： 第2部分： 力学性能： GB/T 3880.2—2012[S].

[10]刘浩. ANSYS 15.0有限元分析从入门到精通[M]. 北京： 机械工业出版社， 2014： 95107.（编辑武晓英）