分组量子遗传算法在混凝土重力坝坝体综合弹性模量反演中的应用

贾春兰，朱　凯

(1.新疆维吾尔自治区水利水电勘测设计研究院，新疆 乌鲁木齐 830000；2.河海大学 水利水电学院， 江苏 南京 210098)

分组量子遗传算法在混凝土重力坝坝体综合弹性模量反演中的应用

贾春兰1，朱凯2

(1.新疆维吾尔自治区水利水电勘测设计研究院，新疆 乌鲁木齐 830000；2.河海大学 水利水电学院， 江苏 南京 210098)

摘要：通过编程建立Matlab与有限元软件命令调用接口，建立基于分组量子遗传算法的混凝土重力坝坝体材料力学参数有限元反演模型。利用工程实测值与有限元模型计算值建立适应度函数，通过分组量子遗传算法智能寻优，实现混凝土重力坝力学参数反演。以某混凝土重力坝为例对其各分区综合弹性模量进行反演，并与传统遗传算法反演结果进行对比，结果表明本方法反演精度及运行速度较均高于传统遗传算法。

关键词：分组量子遗传算法；混凝土重力坝；有限元；适应度函数

水工结构设计以及工程结构的应力应变、裂缝形成机理分析很大程度上取决于岩土工程介质的物理力学参数，参数的选取可以用来反馈和检验水工结构的设计和施工。混凝土重力坝由于其运行条件复杂，运行工况多样等特点导致其结构物理力学参数往往随着时间的增长而发生变异，及时更新这些参数对于混凝土重力坝安全监控具有十分重要的意义。传统智能优化算法寻优结果依赖于初始参数的选取，并且具有寻优效率低、精度差的缺点[1-2]。反演分析是一个典型的复杂非线性函数优化问题，理想的智能优化求解途径是各种理论经验丰富的全局优化算法。Friswell采用遗传算法对结构损伤问题进行了判定[3]，Sankar采用遗传算法对地球物理力学参数进行智能寻优[4]，李守巨等提出了基于遗传算法的岩体初始应力场反演方法，并对相应岩石和混凝土材料参数进行反演分析[4-5]。

本文通过引入分组量子遗传算法，实现理想目标函数的智能优化寻优，利用Abaqus高效内核求解器，建立基于有限元法计算结果的分组量子遗传算法反演模型，以有限元计算值与实测值建立适应度函数，通过Matlab编程，反演水工建筑物结构物理力学参数。并以某混凝土重力坝例对其坝体各分区混凝土综合弹性模量进行反演，通过与工程实测应力、变形值以及传统遗传算法计算结果对比，表明本文算法具有更高的计算精度。

1量子遗传算法与有限元联合反演模型

1.1　分组量子遗传算法

量子遗传算法(quantum genetic algorithm，QGA)以量子理论为基础，采用量子位概率编码表示染色体，通过不断更新量子旋转门的作用来更新和优化种群，达到搜索的目的[6-10]。本文采用分组量子遗传算法，通过将个体分层、分组，并将每层按类进行不同的量子计算，对解空间进行多方寻优，增加染色体多样性，从而保证了解的多样性。

一个量子位可以处于0态、1态、以及|0〉和|1〉之间的任意叠加态。可以表示为：

(1)

(2)

(3)

在分组量子遗传算法中，量子旋转门可以表示为:

(4)

量子门更新过程可以表示为:

(5)

(6)

所以，可以得出：

(7)

因此可以看出，通过采用不同的量子叠加态形式，分组量子遗传算法可以保持染色体及相应种群的多样性[11]，相应算法流程图如图1。

图1分组量子遗传算法流程图

1.2　量子遗传算法与有限元联合反演模型

商业有限元软件Abaqus具有高效内核求解器，通过二次开发可以建立Abaqus与Matlab程序的用户接口，从而极大提高反演效率。基于有限元计算结果，本文建立量子遗传算法反演模型，以工程实测值与有限元计算值差值建立适应度函数，通过Matlab编程实现了水工结构材料力学参数的反演，具体步骤如下：

(1) 利用Matlab建立Abaqus有限元程序调用接口，通过System命令调用Abaqus模型INP文件和材料本构Fortran子程序文件，并利用Abaqus有限元高效内核进行求解。

(2) 在步骤(1)编辑完成INP文件后，利用Elprint命令，将Abaqus有限元计算结果文件特征单元变形信息输出。通过Matlab中Fopen命令调用并计算特征单元误差适应度函数。

(3) 编写分组量子遗传算法子程序，并对步骤(2)中特征单元适应度函数进行寻优计算。

(4) 利用Matlab语言中Num2str命令修正命令流文件中的反演参数，并实现量子门旋转更新，得到下一代种群。

(5) 重复步骤(1)到(4)，直至目标函数达到要求的精度值Eps。

分组量子遗传算法与有限元联合反演模型计算流程图见图2。

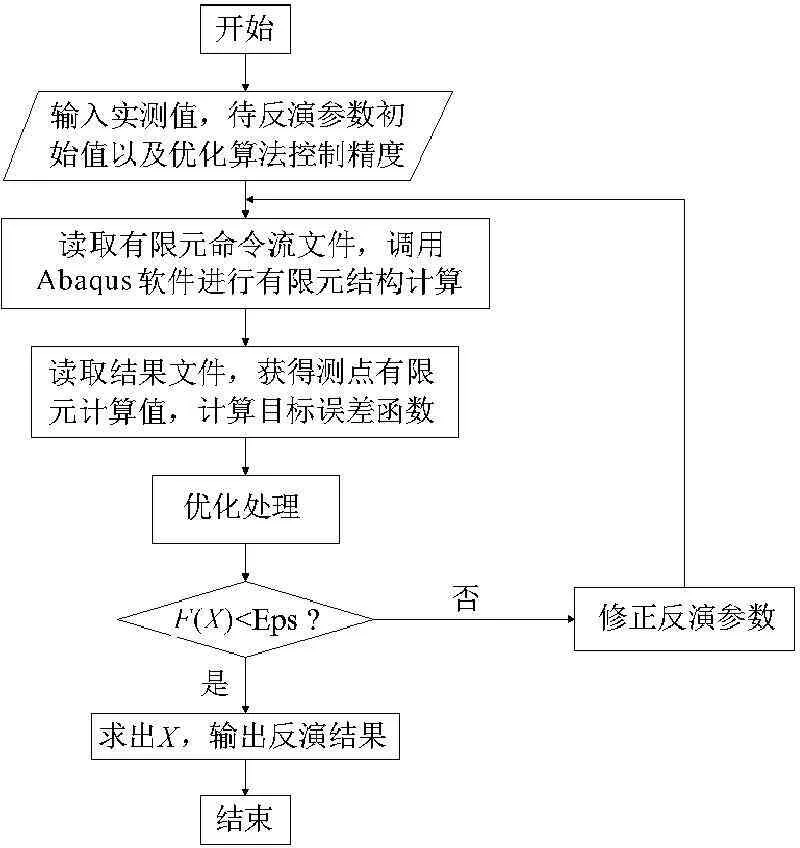
图2分组量子遗传算法与有限元联合反演模型流程图

2工程实例

2.1　工程简介

某水电站枢纽位于云南省丽江市境内，左岸是永胜县，右岸是古城区。枢纽主要由碾压混凝土重力坝、溢流表孔、泄槽及消力池、右岸泄洪(冲沙)底孔、左岸冲沙底孔、坝后厂房及进厂交通洞等永久建筑物及导流隧洞、围堰等临时建筑物组成。混凝土重力坝最大坝高160 m，总库容9.13×108m3，装机容量为2 400 MW。碾压混凝土重力坝下游效果图见图3。本文选取重力坝左岸挡水6#坝段利用坝体原型监测资料对坝体各分区混凝土综合弹性模量进行反演分析。

图3　坝体下游效果图

6#坝段坝体混凝土分区图见图4，坝体三维有限元模型见图5，模型由43 565个单元组成，其中顺河向方向自坝踵向上游延伸2倍坝高，自坝址向下游延伸3倍坝高，横河向方向取整个坝段宽度作为模型范围。有限元计算过程中三维有限元模型约束底部三个方向位移，上下游及左右岸立面均约束法向位移。

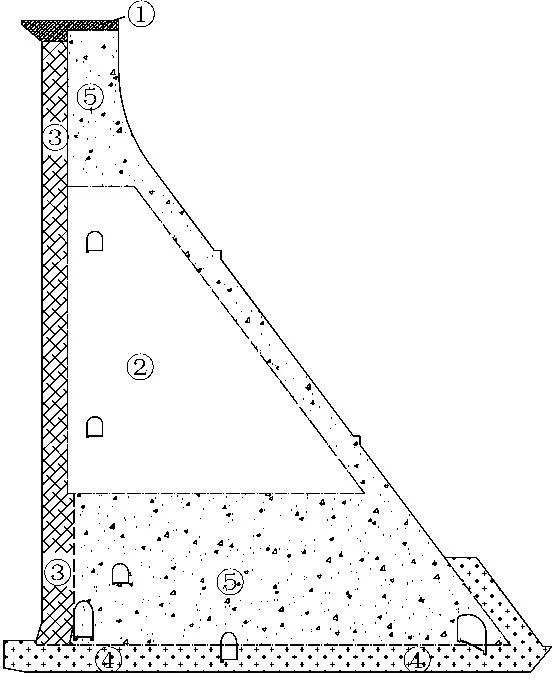
图4　6#坝段坝体混凝土分区图

图56#坝段三维有限元模型

2.2　参数反演结果分析

本文对6#坝段混凝土各分区综合弹性模量进行反演分析，选取正常蓄水位工况(坝前水位123 m，坝后水位15 m)，以6#坝段正倒垂线(见图6)各测点所测坝体水平位移与有限元模型计算结果中相应测点水平位移差值建立误差适应度函数，并利用分组量子遗传算法进行参数反演。预先设定的各分区坝体弹模取值范围为12 GPa～32 GPa。

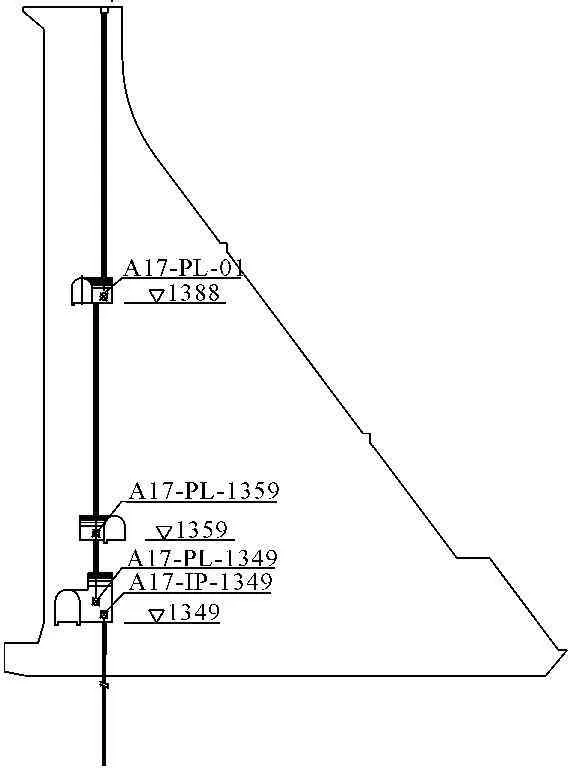
表1　两优化算法反演模型计算结果与比较

(1) 分组量子遗传算法搜索最佳值精度更高，较传统遗传算法GA更逼近各分区坝体弹模实测值。

(2) 由于分组量子遗传算法采用量子概率编码增强了种群多样性，导致分组量子遗传算法搜索平均值略差于GA平均值，但分组量子遗传算法能够有效避免GA方法出现局部极小值的缺陷。

(3) 就反演平均拟合值与最佳拟合值来说，分组量子遗传算法均优于GA方法。就优化算法计算效率来说，两种方法寻优计算的最快搜索时间相差不大，但分组量子遗传算法平均搜索时间更短，大大提高了运行效率。

利用反演计算的坝体各分区混凝土综合弹性模量对该混凝土重力坝进行结构正分析，并将两种算法反演计算值与相应坝体应力计测点实测值对比分析，结果见表2。

表2　测点应力实测值与反演计算值对比

由表2知，基于分组量子遗传算法反演的坝体混凝土力学参数进行结构正分析所得特征节点的应力计算值更接近实测值，具有更高的计算精度。对两种算法分别进行20次独立搜索，分组量子遗传算法算法精度和计算效率具有更大的优势，能更快的搜索到较优个体，且不依赖初始种群，具有全局收敛特性，大大提高了反演分析进程。

为了反映分组量子遗传算法在坝体分区弹模反演中的有效性，本文将分组量子遗传算法与传统遗传算法两种算法反演的坝体各分区综合弹性模量反演结果(搜索最佳值)分别代入有限元模型中，选取2002年1月28日—2002年2月15日大坝蓄水期间10组工况，进行有限元结构计算，并与PP5测点坝顶水平位移水压分离分量进行对比分析，见图7。由图7可知，分组量子遗传算法反演出的坝体分区弹模应用到有限元中的计算结果与实测坝体位移规律一致，并且相比传统遗传算法具有更高的计算精度。

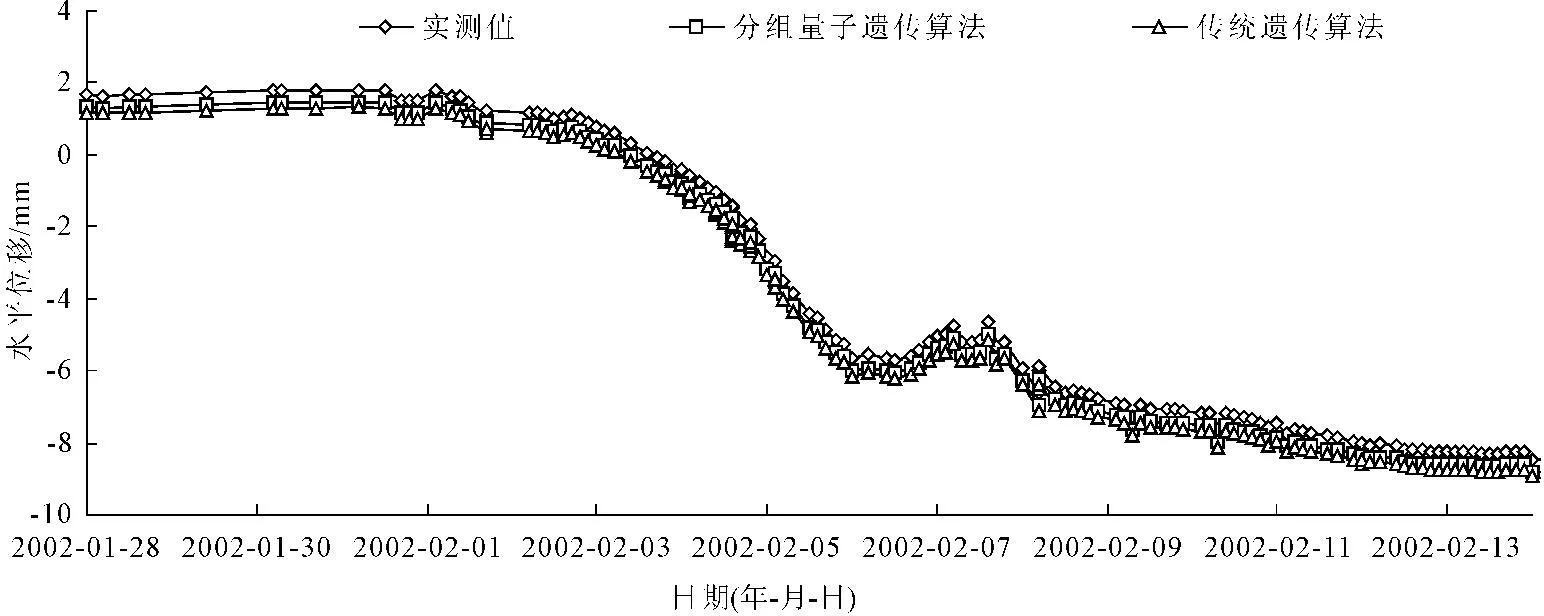
图7PP5测点坝体水平位移分布曲线

3结论

本文通过构建Abaqus有限元软件与Matlab程序调用接口，建立基于有限元计算结果的分组量子遗传算法反演模型，通过与坝体应力、变形实测值以及传统遗传算法反演结果进行对比分析，可以得出以下结论：

(1)分组量子遗传算法通过对量子信息进行分层、分组表示，并对解空间进行多方寻优，增加染色体多样性，从而确保算法收敛于全局最优解，具有收敛速度快、收敛精度高的特点；

(2)应用分组量子遗传算法与有限元联合反演法，以实测值与有限元计算值差值建立适应度函数，反演了某混凝土重力坝各分区的综合弹性模量，反演结果较传统遗传算法精度更高，效率更快；

(3)将分组量子遗传算法反演的坝体弹模应用到坝体三维有限元计算中，并与坝体应力、变形实测值进行对比分析，结果表明反演结果能够代表坝体各分区综合弹性模量水平，具有一定实践应用价值。

参考文献：

[1]向衍，郑东健，何旭升，等.基于MSC.Marc的物理力学参数反演[J].水电能源科学,2003,21(4):7-10.

[2]李波，徐宝松，武金坤，等.基于最小二乘支持向量机的大坝力学参数反演[J].岩土工程学报,2008(11):1722-1725.

[3]Friswell M I, Penny J E T, Garvey S D. A combined genetic and eigensensitivity algorithm for the location of damage in structures[J]. Computers & Structures, 1998,69(5):547-556.

[4]李守巨，刘迎曦，王登刚.基于模拟退火算法的含水层参数非线性反演[J].西安交通大学学报,2001,35(5):546-548.

[5]李守巨，刘迎曦，王登刚.基于遗传算法的岩体初始应力场反演[J].煤炭学报,2001,26(1):13-17.

[6]梁昌勇，柏桦，蔡美菊，等.量子遗传算法研究进展[J].计算机应用研究,2012,29(7):2401-2405.

[7]孙伟，何蕴龙.基于改进遗传算法的垫层区混凝土热学参数反演和早期裂缝成因分析[J].武汉大学学报：工学版,2014(2):193-200.

[8]陆梓端，高茂庭.基于改进遗传算法的支持向量机参数优化[J].网络新媒体技术,2010,31(5):11-15.

[9]杨杰，杨丽，李建伟，等.基于改进遗传算法-偏最小二乘回归的大坝变形监测模型[J].西北农林科技大学学报:自然科学版,2010,38(2):206-210.

[10]董起广，周维博，李云排，等.改进遗传算法在泾惠渠灌区水文地质参数求解中的应用[J].中国农村水利水电,2014(5):27-30.

[11]郭海燕，金炜东，李丽，等.分组量子遗传算法及其应用[J].西南科技大学学报:自然科学版,2004,19(1):18-21.

DOI:10.3969/j.issn.1672-1144.2015.04.018

收稿日期：2015-03-17修稿日期：2015-04-27

基金项目：国家自然科学基金重点项目(41323001；51139001)；水利部公益性行业科研专项经费项目(201201038；201301061)

作者简介：贾春兰(1987—)，女，重庆万州人，硕士，主要从事工程渗流方面的研究工作。E-mail：544960676@qq.com

中图分类号：TV642.3

文献标识码：A

文章编号：1672—1144(2015)04—0091—05

The Application of Classified Quantum Genetic Algorithm in the Reversion Calculation of Comprehensive Elastic Modulus of Concrete Gravity Dams

JIA Chunlan1, ZHU Kai2

(1.XinjiangSurveyandDesignInstituteofWaterResourcesandHydropower,Urumqi,Xinjiang830000,China;2.CollegeofWaterConservancyandHydropowerEngineering,HohaiUniversity,Nanjing,Jiangsu210098,China)

Abstract：The calling interface was established between MATLAB and the finite element software ABAQUS and the finite element inversion model based on the classified quantum genetic algorithm was further established to calculate the mechanical parameters of the concrete material. And then the fitness function was determined by the calculation of the finite element calculated value and the measured value as well as the optimization of the classified quantum genetic algorithm At last, a certain concrete dam was taken as an example to calculate the comprehensive elastic modulus of each section and the results were compared with that of the conventional genetic algorithm. It is verified that both the accuracy of inversion calculation and running speed of the above method are better than those of the conventional genetic algorithm.

Keywords:classified quantum genetic algorithm; concrete gravity dam; finite element; fitness function