基于蒙特卡洛方法的压力钢管水锤风险分析

张　静，王长新

(新疆农业大学 水利与土木工程学院， 新疆 乌鲁木齐 830052)

基于蒙特卡洛方法的压力钢管水锤风险分析

张静，王长新

(新疆农业大学 水利与土木工程学院， 新疆 乌鲁木齐 830052)

摘要：水电工程中压力钢管的结构安全对整个电站的安全运行有着重要的影响,而水锤对管道的安全性影响非常大，因而以特吾勒水电站回填式压力钢管为例，建立了计算水锤压力风险的功能函数，利用蒙特卡洛方法计算了考虑和不考虑轴向应力两种情况下的水锤压力风险值，并具体计算分析了各随机变量对综合风险的影响，结果表明利用第四强度理论计算水锤压力风险更加符合实际，为压力钢管的设计提供了依据。

关键词：随机变量;蒙特卡洛法;回填钢管;风险值

压力钢管是水电工程中输水建筑物的重要组成部分,它的结构安全对整个电站的安全运行有着重要的影响[1]，而影响管道安全的重要因素为水锤压力。因而在以往研究压力钢管的风险时，主要集中在水锤压力的计算方法[2-4]、水锤及其他随机变量的概率分布和统计特征[5-8]以及风险计算方法上 ，但并未系统的计算水电站压力钢管的水锤风险率。本文在国内外研究学者的研究基础上，结合乌苏市特吾勒水电站回填式压力钢管，利用蒙特卡洛法并借助MATLAB软件计算了压力钢管在考虑和不考虑轴向应力两种情况下的水锤压力风险值，并具体分析计算了各随机变量对综合风险的影响，为设计和评估压力钢管的可靠安全方面提供依据。

1蒙特卡洛法

1.1　蒙特卡洛法

到目前为止，计算风险的方法主要有：直接积分法、一次二阶矩法、蒙特卡洛法、梯度优化法和响应面法。蒙特卡罗法随着模拟次数的增加，其计算结果将逐渐趋近于精确解，因此被认为是一种精确的计算方法，因而选择蒙特卡洛方法。蒙特卡洛法又称为随机抽样法，其基本方法是通过某种算法从相应的概率分布中人为生成一组特殊随机变量值，再进行大量模拟运算，通过检验模拟运算的结果来估算风险。蒙特卡洛方法的精确性依赖于模拟次数，蒙特卡洛法的关键是产生大量已知分布的随机数，而Matlab软件它能快速的产生服从某些分布的随机数并且在短时间内进行大量的模拟运算，这为蒙特卡洛法的运用提供了便利。

1.2　蒙特卡洛法计算步骤

2建立压力钢管风险计算的功能函数

影响结构状态的基本变量x1，x2,…,xn，按其属性，可归为两个基本变量，即强度随机变量R和应力随机变量S，于是有：

(1)

其中，xRi是与结构强度有关的量；xSj是与应力有关的量，例如力、力矩、温度等。经过这样的处理将对多个随机变量的问题转换为两个随机变量的问题，便于分析计算，由此结构的功能函数可简写为：

Z=g(R,S)

(2)

对于公式(2)，可以根据不同的情况取不同的具体形式[9]；对于水电站压钢管，将功能函数取为：

Z=R-S

(3)

这里，压力钢管的强度随机变量R是由R=R(σs,φ)构成，其中σs为钢材的屈服强度，φ为焊缝系数；而对于压力钢管的应力随机变量S，由于其工作状态处于三维应力状态，但因剪应力τ和径向应力σr对折算应力的影响较小，忽略不计[10]，并且当地形坡度小于20°时，不考虑轴向应力的影响，因而应力随机变量S=σθ，根据《给水排水工程管道结构设计规范》[11](GB50332-2002)建立其功能函数:

Z=R-S=0.55φσs-σθ

(4)

式中：σθ为钢管管壁的最大环向应力。

当地形坡度大于20°时，轴向应力应当加以考虑，因而压力钢管的应力随机变量S=S(σx,σθ)构成，按第四强度理论，建立其功能函数：

(5)

式中：σx为轴向应力。

3随机变量的分布特征与统计特征值

本文在考虑了影响钢管结构安全的主要随机变量的同时，把一些钢材性能参数也看作随机变量加以考虑，如：钢的弹性模量、泊松比、线膨胀系数。其中焊缝系数φ、前池水头Hj、水击压力Hc这3个随机变量可通过相对量获得统计特征值[12]：

(6)

式中： Hmax为钢管的最大水头； Hd为设计水头；Hc为钢管中心水锤实测值；Hwh为水锤设计值；φs为焊缝系数实测值；φg为规范限定值。

统计研究表明[13]，相对量ζj、ζφ和钢材强度σs服从正态分布，其均值，标准差见表1，相对量ζc服从极值Ⅰ型[14]，其均值μζc=1.065，方差为σζc=0.218。

影响钢材性能参数的因素较多，很难确定何种因素起主要作用，且无相关数据进行数理统计分析，根据误差理论、中心极限定理[15]和王长新[16]等人的研究，这里将它们视为正态分布,其均值为设计值，标准差按均值的5%选取。 随机变量的分布特性与统计特征值见表1。

表1　随机变量的概率分布与统计特征值

4回填式压力钢管风险计算实例

4.1　工程概况

特吾勒水库灌区骨干工程配套消能一级电站,电站装机容量为13MW,压力管道引水流量2.34 m3/s,设计发电流量为2.2 m3/s,根据《水利水电工程等级划分及洪水标准》[17](SL252-2000)的规定,属小(1)型Ⅳ等工程,主要建筑物应为4级,次要建筑物应为5级,本工程利用灌溉水发电,按《小型水力发电站设计规范》[18](GB50071-2002)规定,本工程发电厂房等主要建筑物防洪标准为20 a一遇设计。电站引水系统由特吾勒水库放水洞、前池、压力钢管等主要建筑物组成,其中压力管道采用回填式，地埋管管沟采用机械开挖,底宽2.6 m,边坡1∶1，底部设30 cm中粗砂垫层,管顶覆土1.8 m,钢管总长6.91 km,管道纵坡为0.34%～8.413%，管材选用Q235C和X60型螺旋卷焊钢管，管径1.4 m、1.2 m,壁厚为10 mm～16 mm, 静水头362.34 m,最大设计内压水头447.34 m, 属高水头、长距离的水电站压力钢管。

4.2　回填式压力钢管风险计算的功能函数

本工程为满足地形和环境的要求，压力钢管为回填式。由于我国现行的电力行业标准和水利行业标准暂无回填管的计算依据,因此在对回填管的设计和强度检验时所采用的公式主要依据日本的 《压力钢管设计技术标准》,同时参考《给水排水工程埋地钢管管道结构设计规程》[19](CECS141:2002)，采用规范[19]计算理论及水电站压力钢管设计规范中的荷载和材料参数对回填管进行计算，荷载不考虑分项系数。

4.2.1　不考虑轴向应力

本工程管道纵坡为0.34%～8.41%，轴向应力忽略不计，根据公式(4)，此时的环向应力σθ由内水压力和土压力产生[20]，因而建立其功能函数：

(7)

(8)

(9)

式中：W为土压力；rm为管壁半径；ΔX为水平挠度；K为管底支承角相关的系数；e为被动土压力系数;Ep钢的弹性模量；I为单位长度钢管管壁惯性矩。

4.2.2考虑轴向应力，参照第四强度理论建立的功能函数

为了定量的研究轴向应力对风险率的影响，根据式(5)，考虑轴向应力，此时的轴向应力由温度荷载产生，建立功能函数：

(10)

(11)

(12)

式中：α为钢的线膨胀系数;ΔT为温度变化。

4.3　计算成果及分析

经过计算，管道末端承受的内水压力最大，因此本工程选取回填压力钢管的末端截面作为计算点进行风险计算与分析。参照表1各个随机变量的概率分布和统计特征值,使用蒙特卡洛方法并借助Matlab软件计算出回填式压力钢管的风险率Pf，见表2、表3。由表2可以看出，特吾勒水电站的回填式压力钢管的综合风险为0.0015236，虽然用两种功能函数计算出的风险率均满足要求，但是在不考虑轴向应力情况下计算的风险值是用第四强度理论计算出来的11倍。从表3可以看出，在模拟次数为1000万次时相对于将钢的弹性模量、泊松比和线膨胀系数这些参数作为常量时，将钢的弹性模量、泊松比和线膨胀系数这些参数作为变量时，风险只增加0.59%，因而可知是否将其作为随机变量对压力钢管水锤风险的影响很小；而当σ=1.5σj时计算得到的风险率是当σ=σj时的16倍，说明各个随机变量标准差的选取对计算压力钢管风险的影响重大。

表2　回填式压力钢管的综合风险

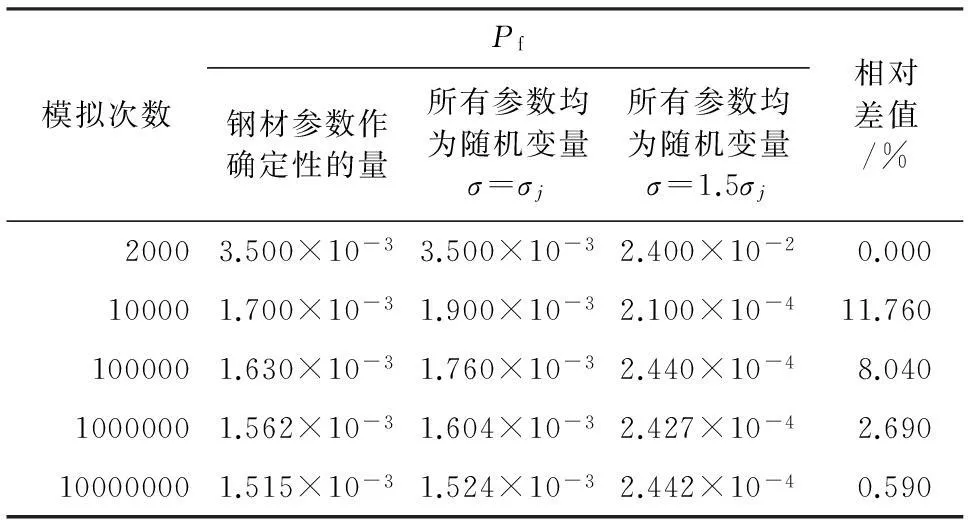
表3　考虑钢材性能参数与否的风险值对比计算结果

为了得到某一随机变量对回填压力钢管的综合风险的影响，单独改变某一个变量的标准差σ，其他随机变量的标准差为设计值σj，σj的取值参照表1，标准差的变化范围为0.5σj～1.5σj，计算其风险率，计算成果见表4和图1～图3,由表4的最后一行得，水锤压力的不确定性对风险的影响最大，其风险变化可达到1.12×10-2。根据图1曲线可知随着实际值与设计值比值的增加风险率也随着增加，两者风险率的增长速度近似，从而可得钢材强度和焊缝系数的不确定性对风险的影响效果几近相同；图2中三条线接近水平，说明钢的弹性模量、泊松比和线膨胀系数的不确定对压力钢管的水锤风险的影响是很小的，其引起的风险变化最大的也只有1.27×10-5,从而在设计中我们完全可以把材料性能参数看做是确定量;由图3曲线可知水锤压力的不确定性对风险的影响可分为两部分，当实际标准差小于设计值时风险率的增长速度较小，当大于时风险率的增长速度明显加大，可见如果选择不当将会带来较大的风险。

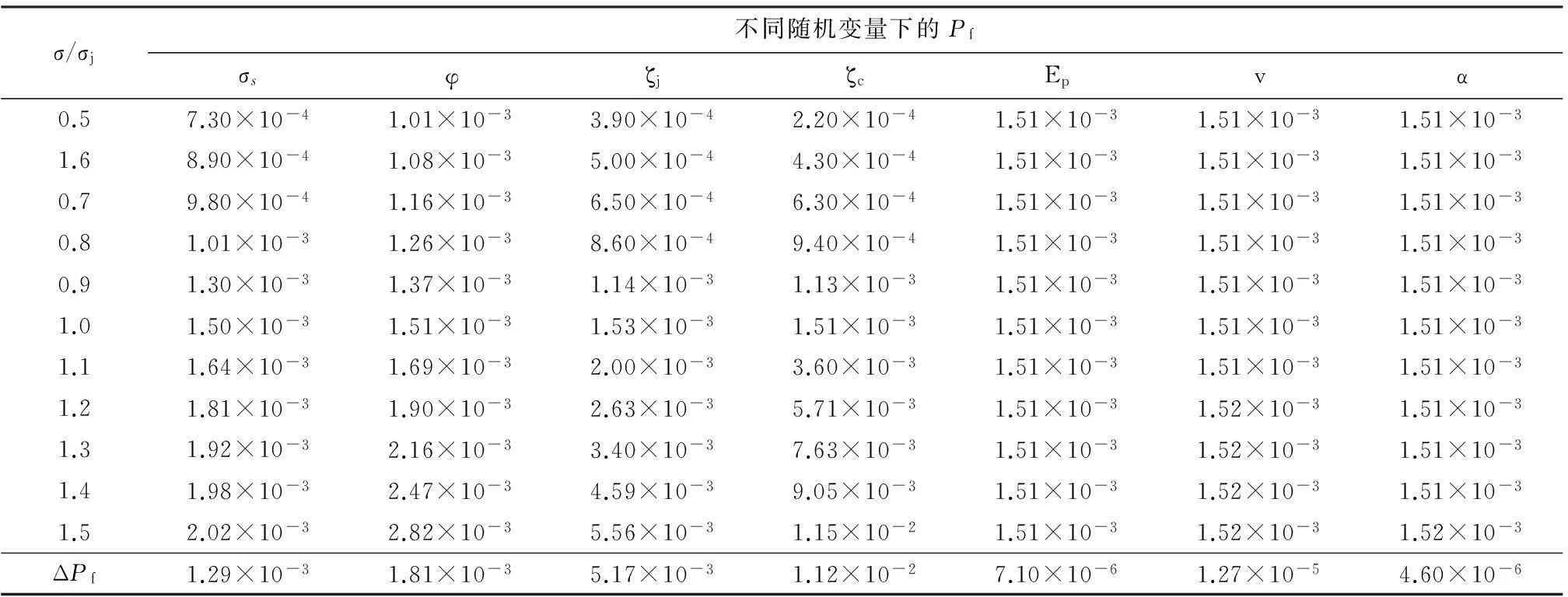
表4　各随机变量的不确定性对风险Pf的影响

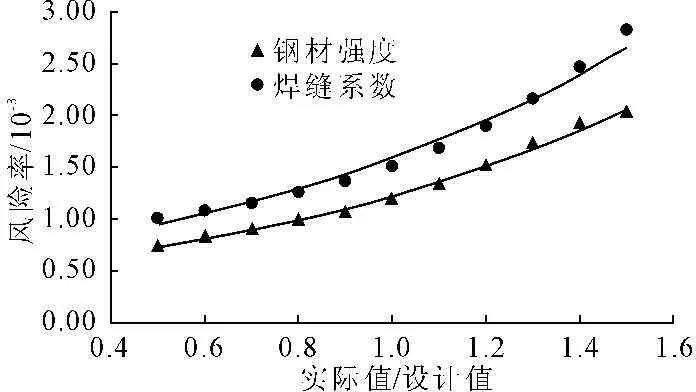
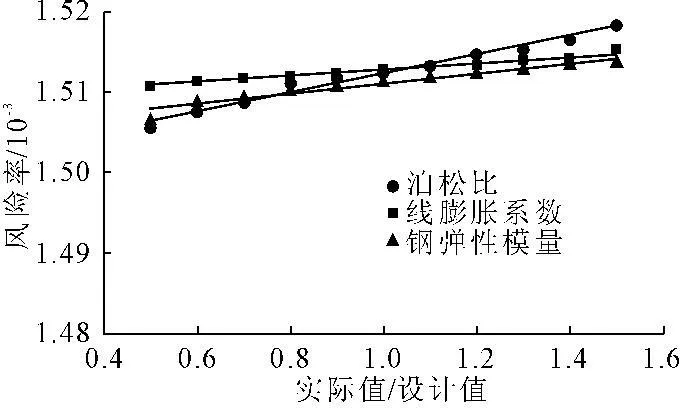
图1　钢材强度σs和焊缝系数φ的不确定性与风险的关系

图2钢的弹性模量、泊松比和线膨胀系数 的不确定与风险的关系

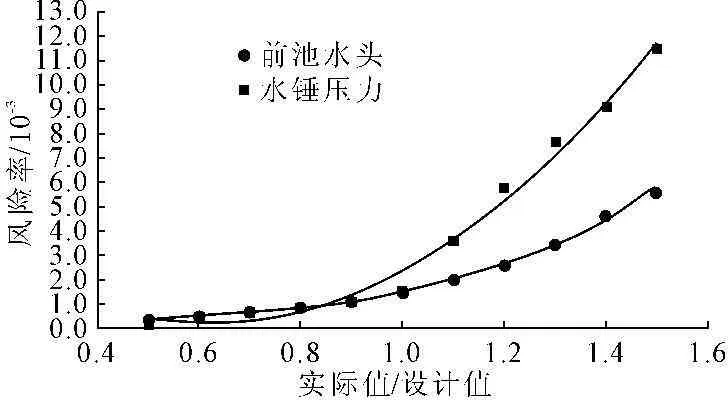
图3静水压力与水锤压力系数的不确定性与风险的关系

5结论

(1) 在设计压力钢管时，我们应采用第四强度理论对钢管进行设计和校核，若采用单一方向的应力，可能导致风险率偏大，对该结构设计过于保守，加大经济的投入。

(2) 材料参数的不确定性对钢管的风险影响很小，所以在压力钢管设计中，我们可以忽略其不确定性的影响，以便简化计算；钢材强度、焊缝系数、前池水头的不确定性对风险的影响虽然没有水锤压力的大，但与材料参数相比要大的多，设计计算时应当考虑。

(3) 对各随机变量风险的影响作了定量的分析，水击压力的不确定性对风险的影响最大，其风险变化可达到1.12×10-2，因而在设计当中我们应当选取合适的水锤计算方法与标准差。水锤压力计算的过小，压力钢管达不到强度要求，计算的过大，造成经济上的浪费。

参考文献：

[1]温婧.水电站埋管结构优化设计与有限元分析[D].邯郸：河北工程大学,2013.

[2]熊水应,王建国,张凯,等.水锤计算分析软件的开发与应用[J].给水排水,2014(11):104-108.

[3]黄兴,王云莉.水电站压力管道系统非恒定流现状及发展动态[J].水科学与工程技术,2014,30(4):28-32.

[4]王川江.新疆准东五彩湾供水工程停泵水锤计算[J].中国给水排水,2014(11):55-57,61.

[5]何英明,侯建国,安旭文.地下埋管可靠度校准分析[J].武汉水利电力大学学报,1999(5):64-68.

[6]袁子厚,陈明祥,何英明.水电站中明管可靠度校准分析[J].重庆建筑大学学报,2007,29(3):75-77,82.

[7]杨绿峰,张伟,韩晓凤.水电站压力钢管整体安全评估方法研究[J].水力发电学报,2011,30(5):149-156,169.

[8]侯建国,李春霞,安旭文，等.水电站地下埋管围岩内压分担率的统计特征研究[J].岩石力学与工程学报,2003,22(8):1334-1338.

[9]何水清,王善.结构可靠度分析与设计[M].北京:国防工业出版社,1993.

[10]刘启钊.水电站[M].北京：中国水利水电出版社，2010.

[11]中华人民共和国建设部，国家质量监督检验检疫总局.GB50332-2002给水排水工程管道结构设计规范[S].北京:中国建筑工业出版社,2002.

[12]何英明,侯建国,张健，等.压力钢管可靠度分析基本变量的统计特性[J].武汉水利电力大学学报,2000,35(5):5-10.

[13]吴世伟,张思俊,余强.坝上游水位变化规律及统计量[J].华东水利学院报,1984(4):66-74.

[14]侯建国,安旭文,李春霞,等.水电站压力钢管水锤压力的统计特征研究[J].长江科学院院报,2004,21(1):4-7.

[15]杨惠莲,张涛.误差理论与数据处理[M].天津:天津大学出版社,1992.

[16]王长新.施工导流风险分析及计算[D].南京:河海大学,1995.

[17]中华人民共和国水利部.SL252-2000水利水电工程等级划分及洪水标准[S].北京：中国水利水电出版社，2000.

[18]中华人民共和国国家质量监督检验检疫总局，中华人民共和国建设部.GB50071-2002小型水力发电站设计规范[S].北京：中国计划出版社，2002.

[19]中国工程建设标准化协会.CECS141:2002给水排水工程埋地钢管管道结构设计规程[S].北京：中国建筑工业出版社，2002.

[20]石长征,伍鹤皋,袁文娜.柔性回填钢管的设计方法与实例分析[C]//第八届全国水电站压力管道学术会议论文集,2014.

DOI:10.3969/j.issn.1672-1144.2015.04.042

收稿日期：2015-02-11修稿日期：2015-03-09

作者简介：张静(1990—)，女，四川安岳人，硕士研究生，研究方向为水力可靠度理论。E-mail:18099175425@163.com 通讯作者：王长新(1957—)，男，辽宁抚顺人，教授，博士生导师，主要从事水工水力学、河流泥沙和水力可靠度理论方面的研究和教学工作。E-mail:wangcx@xjau.edu.cn

中图分类号：TV732.4+1 文献标识码： A 文章编号： 1672—1144(2015)04—0210—05

Risk Analysis of Water Hammer in Steel Penstocks Based on Monte Carlo Method

ZHANG Jing, WANG Changxin

(CollegeofHydraulicandCivilEngineering,XinjiangAgriculturalUniversity,Urumqi,Xinjiang830052,China)

Abstract：The safety of steel penstock structure in hydropower projects has an important influence on the safe operation of the whole power plant, and the water hammer has a great impact on the safety of the pentocks. Based on this, a performance function was developed to calculate the risk caused by water hammer in the backfill penstock of Tewule hydropower station. Monte Carlo method was adopted to calculate the risk caused by water hammer with or without the consideration of axial stress, and the effect of random variables on the comprehensive risks were analyzed. The results indicate that the fourth strength theorem is more suitable for the risk calculation. This will provide the theoretical basis for the design of steel penstocks.

Keywords:random variables; Monte Carlo method; backfill penstock; risk value