小展弦比翼大攻角水动力数值计算方法

周广礼，姚朝帮

(海军工程大学 舰船工程系，湖北 武汉430033)

0 引 言

小展弦比三维舵翼的水动力预报是船舶操纵性预报的前提和基础，在以往进行舵初步设计时主要采用相关翼型已有的试验资料进行展弦比换算［1］或基于势流理论的方法来得到翼的水动力性能［2］，然而采用展弦比换算方法所得计算结果误差较大，基于势流理论的方法并不能准确预估大攻角翼的水动力性能而且无法对几何形状较为复杂的舵(如半悬挂舵、襟翼舵)的水动力进行预估。

随着CFD 技术的快速发展和计算机性能的不断提高，采用商用软件来预报小展弦比翼水动力性能成为翼水动力预估的重要手段。文献［3-4］表明采用定常计算方式结合N -S 方程(RANS 方法)及现有湍流模型能够较为准确的得到小攻角下翼的升阻性能，然而对于大攻角下翼尾端出现非定常分离流动后采用RANS 方法还不能合理预报翼的水动力性能，黄少峰［5］的研究结果指出，采用考虑和不考虑物面剪切应力的方法均不能准确预报大攻角翼升力系数，而对这2 种方法的计算结果取平均可作为翼升力系数的参考值;李锋［6］等则通过在N-S 方程中添加自定义粘性项得到了适用于预报特定Mach 数翼型大攻角周期性绕流的方法。在不考虑计算量的情况下，能否通过采用非定常计算方式结合N -S 方程(URANS 方法)来精确捕捉翼尾端的分离流动及如何通过细化网格来提高宏观力预报精度还有待进一步研究。

另一方面，近年来计算机性能的快速提高使得应用LES 和DES 等方法预报翼水动力性能成为可能，陈江涛［7］等应用基于S -A 湍流模型的DES 方法模拟了3.5 ×106＜Re ＜8.4 ×106时的圆柱绕流，并较为准确的得到了流场信息;Breuer M［8］等应用RANS、DES 与LES 方法模拟了高雷诺数下大攻角(18°)平板绕流，结果表明DES 方法与LES 方法得到的流场信息更为相似;Huang B［9］等应用DES 方法较为准确模拟了水翼表面的非定常空化流动。然而对于水翼尾端的分离流动能否通过DES 方法来准确模拟及方法的适用条件还有待进一步探讨。

本文应用Fluent 商用软件以NACA0018 小展弦比翼为研究对象，重点探讨了不同雷诺数下计算模型适用性及不同模型下网格离散对大攻角翼水动力计算结果的影响规律，并对翼失速后尾端产生的非定常分离涡进行模拟和探究。

1 控制方程及适用条件

本文以纳维-斯托克斯方程(N -S 方程)作为求解不可压缩牛顿流体运动的基础方程。RANS方程是对N - S 方程进行时均化得到，RANS 与URANS 方法分别基于RANS 方程采用定常与非定常的计算方式进行数值求解。LES 模型是从三维非定常N-S 方程出发，通过滤波计算将小于某一格子尺度的小涡诸量过滤掉从而只针对大涡运动进行模拟的数值计算方法，其中RANS 和LES 方程可以表达为同一种形式:

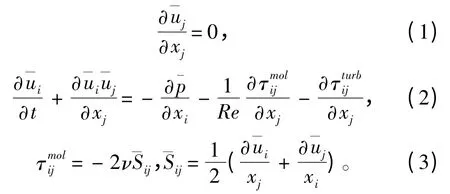
式中:p 为静压;μ 为流体粘度;ui和uj为速度分量。Re 为特征长度雷诺数;表征由分子运动引起的动量传输，其具体表达见式(3)。在RANS 与LES 方程中(·)项分别代表大尺度涡的计算项和时均项，为了更好地模拟由湍流运动引起的动量传输，在LES 与RANS 的动量方程(2)中增加非线性对流项

在应用LES 模型时对计算空间网格的离散有较高的要求，具体如下:1)近壁面第1 层网格处y +值小于1;2)各方向上的网格尺度扩展比率在1.15左右;3)各方向上的网格尺度相差不大。

如果在整个计算域中均按此原则进行网格划分必然使得网格数量急剧增多，为减小网格数量Spalart［10］提出了DES 方法，该方法结合了RANS 和LES 方法的优点，应用DES 方法进行计算时，物体近壁面采用基于RANS 方程的湍流模型进行求解而针对远离物面的的分离区域则采用LES 模型进行求解，其在分离涡计算方面的精度要高于RANS、URANS 方法而所需网格数量要远小于LES 方法。

本文计算中涉及RNG k －ε、SST k －ω 和SA 三种湍流模型，详细推导过程和参数的取值可参考文献［11］。

2 计算对象与网格划分

2.1 计算对象

文中以NACA0018 小展弦比翼作为计算对象，翼平面形状为矩形，模型主尺度见表1。

表1 计算模型主尺度Tab.1 Main dimensions of computational model

2.2 边界条件及网格划分

由于计算对象关于过展长中点剖面对称，为减小计算量，设置过展长中点剖面为对称面取1/2 翼进行计算，计算域以及边界条件(见图1)设置如下:

1)入口:入口距离翼导边4 倍弦长，边界条件设置为速度入口;

2)出口:出口距离翼随边7 倍弦长，边界条件设置为压力出口，压力为未扰动时边界压力;

3)流域的外边界距翼的纵向中心线四倍弦长，边界条件设置为速度入口，速度大小方向与入口相同;

4)在翼表面定义无滑移、不可穿透边界条件。

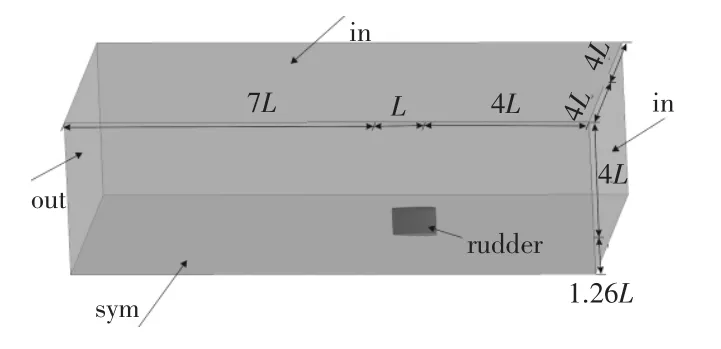
图1 计算域Fig.1 Computational domain

图2 翼表面网格划分Fig.2 Grid partition on hydrofoil

为更好的控制各方向上的网格尺度扩展比率和提高网格质量，在翼型外围采用多块分梯度加密的方法并在翼顶部与外围进行O 型拓扑处理，翼表面网格划分如图2 所示。

3 数值计算分析

3.1 计算模型适用性

在应用CFD 进行预报时，计算条件尤其是雷诺数的大小是计算模型选取的重要依据，试验资料［12］表明当雷诺数大于1.2 ×105时仅失速角随雷诺数的增大而增大，在失速角范围内一定攻角下雷诺数的增大不会引起翼升阻系数的变化，由于试验测得的升力系数可靠性较高(误差3%以内)，本节以Re=2.7 ×105时的升力试验结果作为不同雷诺数下宏观力预报准确性的评判依据来探讨不同雷诺数下翼未失速时计算模型的适用性。

3.1.1 Re ＜106时计算模型适用性

为考察Re ＜106时计算模型适用性并减小由网格离散与计算方式带来的影响，以极细网格(满足DES 方法要求，网格数320 万，y + ～1)为基础，采用非定常计算方式(时间步长取0.0001s)，开展了Re=2.7 ×105、不同模型下10°、15°及18°攻角翼升阻系数的数值预报并与试验值进行对比(见表2)。计算结果表明:当Re ＜106时，采用URANS 方法的预报精度较高，其中以RNG k－ε 湍流模型的预报结果与试验值吻合最好，DES SST 与DES SA 模型计算所得升力系数较试验值偏差较大。

翼尾端流动分离位置和分离范围的准确模拟是准确预报宏观力的关键，由不同湍流模型计算结果与所得的流场信息(见图3)可知，在Re ＜106时，采用DES 方法得到的流动分离位置明显靠前，其模拟得到的流动分离现象与实际流动偏差较大。

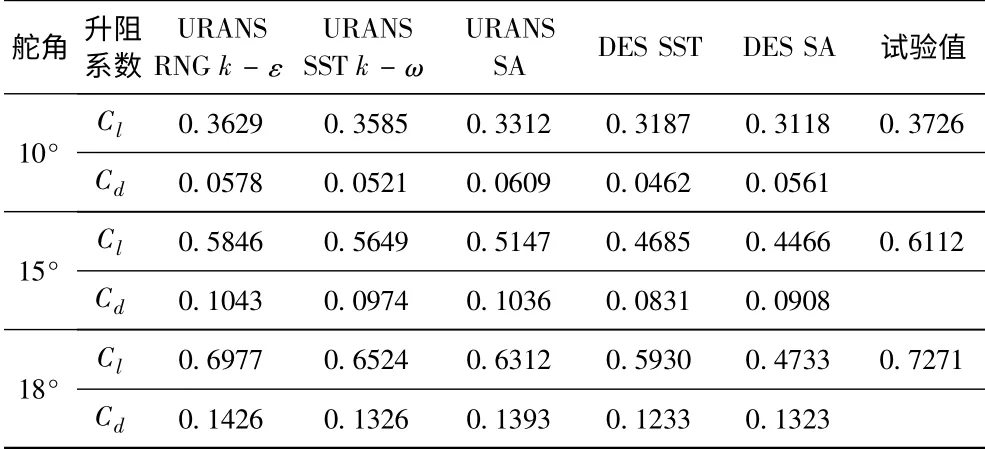
表2 Re=2.7 ×105 时不同计算模型翼升阻系数计算结果Tab.2 Lift and drag coefficients calculated by different models at Re=2.7 ×105

图3 18°攻角下不同模型计算所得展长中点剖面处流场信息Fig.3 Flow fields of mid-elongation section calculated by different models at 18° incidence

3.1.2 高雷诺数下计算模型适用性

为探讨高雷诺数下计算模型适用性，文中对比了1.35 ×106＜Re ＜2.7 ×107时翼升阻系数的计算结果 (见表3)，由表3 可知，在高雷诺数下URANS 方法的预报精度均较低，而当Re ＞2.7 ×106时，DES 方法的计算结果与试验值吻合较好。

表3 高雷诺数时不同计算模型下翼升阻系数对比Tab.3 Comparison of lift and drag coefficients calculated by different models at high Re

3.2 网格离散的影响

在应用Fluent 软件进行水动力预报时，不同湍流模型采用的壁面处理方式存在差异而且对第1 层网格y+值的要求有一定的参考范围［13］。由表3 可知，在采用加强型壁面函数进行壁面处理时5 种湍流模型对近壁面y+要求较高，在网格不够细(y +＞30)的情况下可以应用RNG k － ε 湍流模型并在近壁面处施加壁面函数进行处理，在处理复杂几何流场计算问题时此模型更适用。

表4 不同湍流模型壁面处理方式及壁面y+参考值Tab.4 Reference value of y+ based on different wall treatment methods

为了研究壁面y +值及网格离散密度对翼水动力计算结果的影响，文中对比了18°攻角下5 套不同网格宏观力系数的计算结果(见表5)，为满足DES 模型的网格离散要求将网格进行细化(fine-1、fine-2)，在应用URANS 和DES 方法时分别取计算雷诺数Re=2.7 ×105和2.7 ×107。由表5 可看出，在同一模型下壁面y +值的选取对计算结果的影响较大，当y + 在30 ～110 范围内时，采用URANS RNG k －ε 模型结合壁面函数的方法较其他模型所得结果相对较为合理但误差仍较大，当y + 在3 ～30范围时，除URANS RNG k － ε 模型计算结果相对较为可信外，其余模型误差均较大，因此在计算大攻角翼水动力性能时，有必要将壁面y +增强至1 左右。通过对比相同y +下粗网格与细网格的计算结果可知在满足y+ ～1 的条件下，增加网格密度可提高计算精度，如果模型较为复杂(如船后半悬挂舵、襟翼舵)时网格离散很难达到y+ ～1 的条件此时建议采用URANS RNG k － ε 模型并对计算结果进行适当修正。

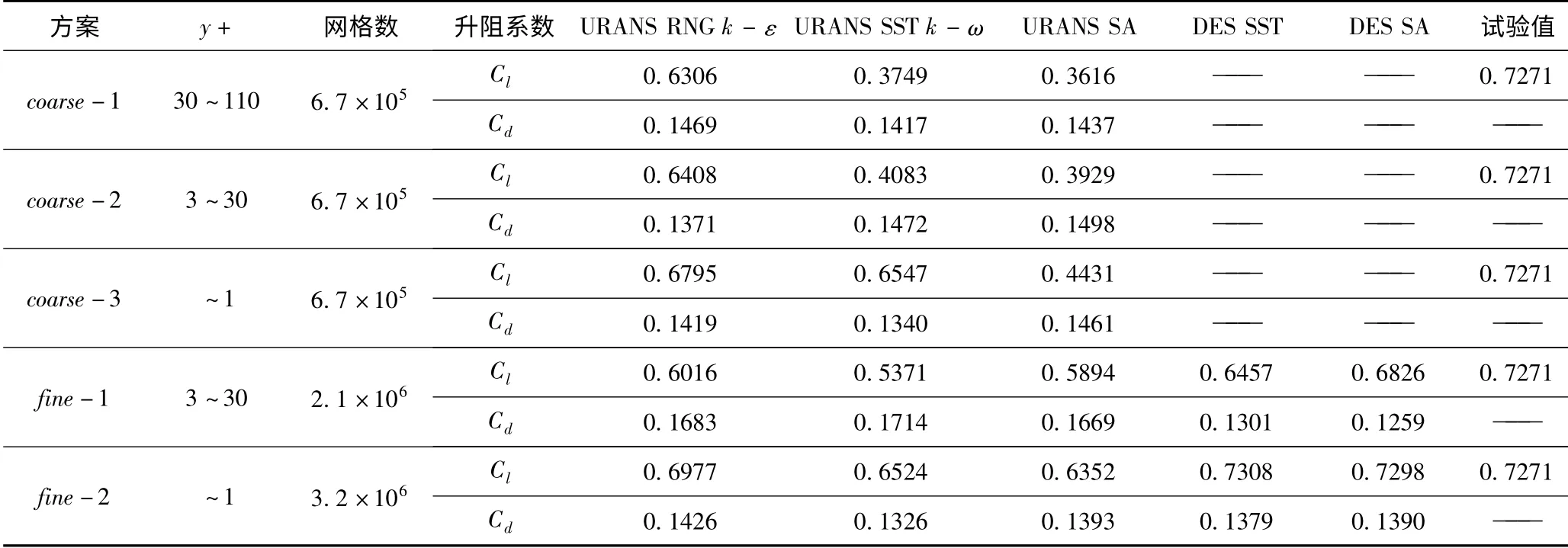
表5 18°攻角不同网格方案下翼升阻系数计算结果Tab.5 Lift and drag coefficients based on different grid partitions at 18° incidence

3.3 翼失速后的流动分离模拟

前面应用非定常计算方式讨论了湍流模型及网格离散对计算结果的影响，然而在工程应用中采用定常计算方式(RANS 方法)可大大减少工程周期，本节探讨了定常计算方式的适用性及其预报不同攻角下翼宏观力的可行性并应用不同方法对翼尾端分离流动进行模拟对比。经计算可知，当计算攻角小于失速角时翼尾端分离范围较小，采用基于RNG k －ε、SST k －ω与SA 湍流模型的RANS 与URANS 方法所得计算结果相差不大且流场信息也基本相同，然而在实际工程应用中RANS 方法预报的失速角存在很大偏差，有必要对翼失速前后采用RANS 与URANS 方法预报结果的偏差进行讨论。如表所示，当计算攻角大于失速角(失速角为21°)时，采用RANS 与URANS 方法所得的升阻系数差别较大。由图4 也可看出，翼失速后采用RANS 与URANS 方法捕捉得到的分离区大小和涡核位置存在较大差异，因此在大攻角下不宜采用RANS 方法进行预报。从计算结果的对比可知，在未知失速角情况下可以通过比较RANS 与URANS 方法的计算结果大致估计攻角是否小于失速角。

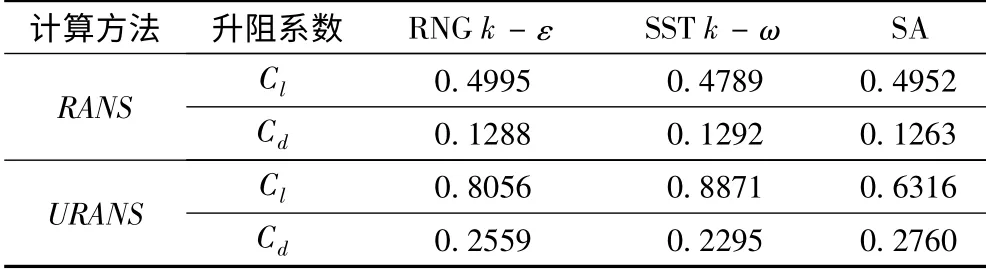
表6 翼失速后(24°攻角)不同计算模型所得升阻系数Tab.6 Lift and drag coefficients based on different turbulence models when hydrofoil stalls

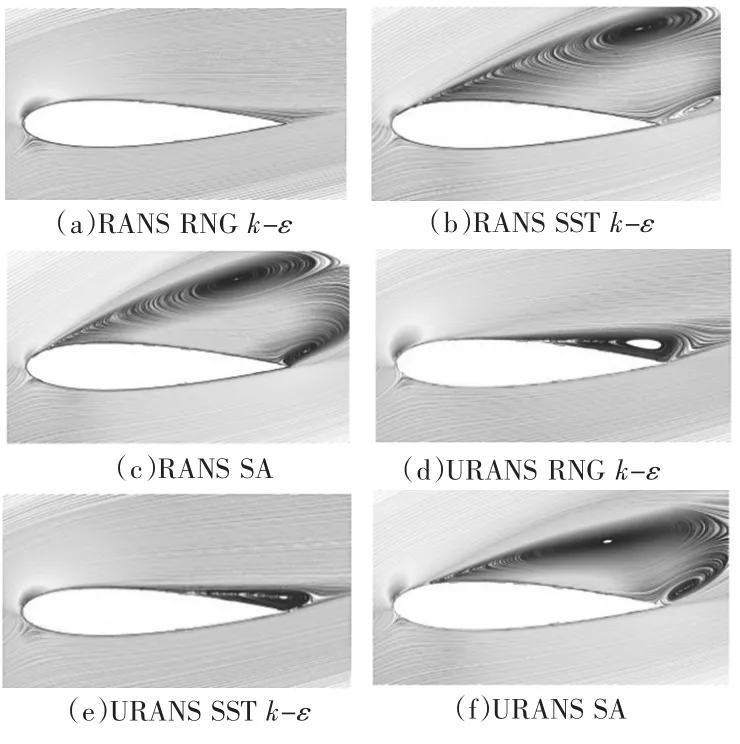
图4 翼失速后(24°攻角)不同计算模型所得展长中剖面流线图Fig.4 Flow fields of mid-elongation section calculated by different models when hydrofoil stalls (24° incidence)

虽然翼失速后采用URANS 方法模拟得到的分离涡与RANS 有较大不同，但URANS 方法所得涡核位置及分离区范围均不随时间发生变化，翼的升阻系数不具有时历波动性。为探究DES 方法对于分离涡的捕捉能力，结合DES 方法的雷诺数适用范围，取Re=2.7×107，攻角35°作为翼迎流条件开展计算，结果表明DES SST 与DES SA 模型计算所得宏观力均表现时历波动性，观察到的分离涡随时间的生成与脱落(见图5)与实际物理现象一致，但其模拟的准确度还需试验验证，DES 模型的优化有待进一步研究。

图5 35°攻角下DES SST 模型计算所得展长中剖面流线图Fig.5 Flow fields of mid-elongation section calculated by DES SST model at 35° incidence

4 结 语

通过对比分析不同计算条件下基于不同湍流模型的RANS、URANS 与DES 方法在大攻角翼型水动力预报中的宏观力计算结果与流场信息可以得出以下结论:

1)计算方法和湍流模型的选取对翼水动力预报精度影响最大且与雷诺数相关;当Re ＜106时，URANS 方法的预报精度较高，其中以RNG k － ε 湍流模型的预报结果吻合最好，而DES 方法的精度较低，当Re ＞107时，采用DES 方法能够得到较为可靠的预报结果;

2)壁面y +对翼型水动力预报精度有重要影响，确保y+ ～1 的同时适当加密网格数量可提高计算精度，在无法满足壁面y+要求时可采用URANS RNG k －ε 模型进行预报并对计算结果进行适当修正;

3)翼型失速后，RANS 与URANS 方法计算所得升阻系数差别较大，这2 种方法均不能捕捉分离涡的时历特性，DES 方法能够观察到与物理现象一致的漩涡结构。905 -909.

［1］梅琴生.船用舵［M］.北京:人民交通出版社，1981.

［2］陈材侃，刘华.解三维水翼绕流的下潜涡环栅格法［J］.船舶力学，2005，9(2):41 -45.CHEN Cai-kan，LIU Hua.A submerged vortex lattice method for calculation of the flow around a three-dimension hydrofoil［J］.Journal of Ship Mechanics，2005，9(2):41-45.

［3］PARK K，LEE J. Influence of endplate on aerodynamic characteristics of low-aspect-ratio wing in ground effect［J］.Journal of Mechanical Science，2008，22(12):2578-2589.

［4］GIM O S，LEE G W. Flow characteristics and tip vortex formation around a NACA 0018 foil with an endplate［J］.Ocean Engineering，2013，60:28 -38.

［5］黄少锋，刘登成，张志荣.基于精细流场分析的大攻角翼型的数值计算与试验研究［C］//2013 年船舶水动力学学术会议，2013:365 -370.

［6］李锋，汪翼云，崔尔杰.翼型大攻角绕流的数值模拟［J］.航空学报，1992.LI Feng，WANG Yi-yun，CUI Er-jie.The numerical simulation of compressible flow around an airfoil at high angle of attack［J］.Acta Aeronautica et Astronautica Sinica，1992.

［7］陈江涛，张培红，周乃春，等. 基于SA 湍流模型的DES方法应用［J］. 北京航空航天大学学报，2012，38(7):CHEN Jiang-tao，ZHANG Pei-hong，ZHOU Nai-chun，et al.Application of detached-eddy simulation based on spalartallmaras turbulence model［J］.Journal of Beijing University of Aeronautics and Astronautics，2012，38(7):905 -909.

［8］BREUER M，JOVIN，MAZAEV K. Comparison of DES，RANS and LES for the separated flow around a flat plate at high incidence［J］. International Journal for Numerical Methods in Fluids，2003，41(4):357 -388.

［9］HUANG B，WANG G，YU Z，et al. Detached-eddy simulation for time-dependent turbulent cavitating flows［J］.Chinese Journal of Mechanical Engineering，2012，25(3):484 -490.

［10］SPALART P R，JOU W H，STRELETS M，et al. Comments on the feasibility of LES for wings，and on a hybrid RANS/LES approach［J］.Advances in DNS/LES，1997，1:4 -8.

［11］张兆顺，崔桂香，许春晓.湍流理论与模拟［M］.北京:清华大学出版社有限公司，2005.

［12］陆惠生，朱文蔚，费乃振，等.敞水舵的试验研究［J］.上海交通大学学报，1981(2):001.LU Hui-sheng，ZHU Wen-wei，FEI Nai-zhen，et al.Experiment study on open rudders［J］.Journal of Shanghai Jiaotong University，1981(2):001.

［13］ANSYS A F.14.0 Theory Guide［J］.ANSYS inc，2011.