基于消费效用无差别的风险性技术创新投资定价

张蕊家陶祥兴胡贵宾（.宁波大学，浙江宁波35；.浙江科技学院，浙江杭州3003）



基于消费效用无差别的风险性技术创新投资定价

张蕊家1陶祥兴2胡贵宾1
（1.宁波大学，浙江宁波315211；2.浙江科技学院，浙江杭州310023）

摘要：随着我国期权市场的开放，新型期权的研究引起关注。在不完备市场下，利用消费效用无差别定价原理对基础资产不可交易的企业技术创新投资进行定价。通过研究三类可投资资本，即债券类、流动性风险类、存在交易损失的非流动性风险类，引入CARA效用函数，建立基于投资效用最大化原则模型，构建满足Bellman方程的投资最优目标函数，得到技术创新投资机会的隐含价值满足的微分方程，并将结果与仅有债券类、或仅有债券类和流动性风险两类投资资产进行对比，讨论和分析非流动性风险类资产及交易损失对技术创新投资定价的影响。

关键词：隐含价值；流动性风险；非流动性风险；交易损失；伊藤公式；技术创新成果评价

一、综述

（一）技术创新投资决策的研究

20世纪50年代，伴随工业社会和经济发展，人们逐渐不满足于加工水平的低效率产生的利润，更加追求高额利润。技术创新带来高效率、高额利润的同时，降低了人工成本。为此，人们更加关注技术创新的来源、加工内部效应与流程等研究。在熊彼特[1]提出的技术创新理论基础上，技术创新的研究迎来复兴阶段。从1970年开始的十年间，Scherer等[2-4]吸取相关理论对技术创新进行拓展性研究。接下来，Lee等[5-7]在已有理论研究基础上，对于系统化、综合化、实用化的追求更深入。技术创新来源于企业对超额利润追求的需要，是将技术层面理论概念的改进与革新进行开发与实践，提高机械工作效率进而降低成本带来经济效益的过程[8]。一些文献从产品和工艺两方面划分创新，产品创新固然会带来一定的超额收益，但易受大量模仿者的冲击而失去优势。相对而言，工艺创新则更易巩固获取边际收益的地位。两者均会受到所在经济市场上其他投资的对冲风险影响。投资的定义[9]包含时间和风险两部分，投资是为获取未来预期回报，而投资一旦发生，成本将具有不可逆性，回报也不确定，为此技术创新投资是具有风险的。由于技术创新具有连续性，则投资的回报可分为一次性回报和现金流回报。技术创新的动态不确定性更需投资决策的灵活性降低投资风险，提高投资回报。特别是伴随着知识爆炸式的发展，技术创新成为“创造与毁灭”的动态变化过程，其不确定性使传统投资决策难以把握变化，获得较好回报。

（二）传统投资NPV研究

传统技术创新投资决策模型往往以离散型函数对回报与投资时间进行刻画，难以满足市场上不同资产投资对冲的动态不确定性与投入生产过程的连续性要求。另外，传统技术创新投资决策模型由于受离散影响，其理论往往基于传统的NPV原理，选择单一——投资（NPV>0）或永不投资（反之）——致使投资缺乏市场实践性，忽略了机动运营价值，从而降低回报收益。NPV的值来源于对预期净现金收入和投资成本的适当贴现并比较两者的差值，其关于投资计划永不变的假设不满足实际企业投资决策。若明知因为外界因素致使投资回报为零，理性经济人不会按原方案进行投资。或者市场出现较高收益低风险的资产投资，理性经济人也不会不选择对冲现有技术创新投资，这对现有投资与时间均有影响。

（三）实物期权的概念及应用

Myers[10]将风险投资机会抽象为一种期权，提出将期权定价理论适用于不确定环境下风险投资的定价思想，将潜在风险的投资机会作为实物期权，以完善传统技术创新投资决策模型的贴现缺乏对灵活性价值的评估。实物期权[11]是对具体投资的选择，其标的资产是某个具体的投资项目，比如技术创新。投资者有权选择对该项目进行实施或放弃，并且可以选择多种投资组合以对冲风险，获得潜在投资价值，因此将期权定价理论应用与不确定风险投资定价结合具有重要意义。针对投资的不同环境需求，实物期权形式也有不同，比如OTA。企业根据实际运营状况，选择放弃投资，将资产变现，项目资产的通用性也在一定程度上决定企业转产的速度与成本。

技术创新投资具有灵活性、不可逆性，并且技术创新投资不单单是流动性资产的投入，还有对于未成型技术实际应用的非流动性固有资产投资。其不确定性不仅仅在于技术的开发与创新，市场的接纳与产品应用也在一定程度上提高了不确定性的程度，特别是宏观市场大环境的波动起主导作用。比如：随着中国加入WTO组织，市场变得更加开放，激发“互联网+”的高速发展，电子商务对实体店铺的冲击，虚拟金融迅猛发展（影子银行）对传统银行运营的影响等。为此，把握技术创新的不确定性创造超额回报不能单单考虑收入与成本的计算方式或者离散的强行贴现，还应将不确定性技术创新抽象为实物期权概念，将其视为投资项目，进行风险对冲，从企业的角度间接获得对于投资时刻与各投资资产分配的把握。这样更符合技术创新的特点，可满足对灵活性价值的评估。本文通过对宏观市场进行分类，从而获得对市场的相对整体把握，针对技术创新研究流动性风险及非流动的成本投入，细化对市场投资的分类。

企业对技术创新的投资关系到企业发展和变革，投资机会的衡量则在经济决策中具有积极指导意义，量化投资机会的隐含价值有助于企业的有效决策。例如某企业拥有对一技术创新的投资机会，该技术创新的提供与采纳需要投资成本，但其风险收益不容忽视。投资实践中，由于该风险收益受到具体市场的影响，企业采用该技术创新的决策和时机均与量化该投资机会的隐含价值有关。正如Myers将风险投资机会抽象为一种期权，提出将期权定价理论适用于不确定环境下风险投资的定价思想，Brennan等[12-14]则将该思想推广运用。本文将技术创新的投资机会作为交易对象，则交易过程可抽象为一种期权交易。

实际上，由于投资者的风险厌恶程度对其消费行为及期权价格也有一定影响，难以满足传统投资机会期权定价中风险中性的投资者假设。为此Follmer等[15-16]将最优等价鞅应用于投资机会期权的定价，而运用投资者主观风险厌恶度的效用无差别定价思想完善了鞅定价理论框架缺乏具体结论的状况。其定价原理是在期初用一定资金换取投资者的投资机会，使得投资者的最大期望效用在期末与原来相等，该资金为投资机会的效用无差别价格，即隐含价值。Kyle认为，做市商对交易市场的管理与操控需要一定资金保障。为此，本文在交易非流动性资产规避投资风险时考虑保障交易的资本损耗。而对于该类资金储备一般采用交易耗时与价格让步（Price concession）测量。目前学术界（如Stoll，Einarsson和Marquis等）通常采用后者进行资金损耗度量，即按照做市商报价差额测定，为此本文采用收益的（1-θ）倍近似作为非流动性资产收益。

二、模型的建立

本研究认为在时间连续情形下，投资收益是一次性回报的，选取投资消费过程与时间Iτ，τ使消费效用期望的最大化如下：

其中投资者的效用函数为U（It），效用关于时间的贴现系数为β。投资过程中，投资者可在任意时刻投资且不可撤销，投资成本固定，设为M，初始资产则为常数a。采用绝对风险厌恶系数λ衡量投资者对风险厌恶程度，并选择CARA效用函数，

（一）市场仅可交易债券类无风险资产

其中μh，σh>0，Ht可取负值，表示技术创新收益处于亏损状态。为方便运算，采用算数布朗运动，则技术创新投资收益Ht变化如下：

dHt=μhdt+σhdZt（2）

若无风险资产利率为r，设{Atϑt>0}代表投资者在t时刻的资产，则投资者的资产变化为：

dAt=(rAt-It)dt（3）

定理1[17]在仅有债券类投资资产的非完备市场中，基于消费效用无差别的投资技术创新机会隐含价值F(h)满足如下微分方程及其条件：

其中-h为投资发生时刻的回报，投资后最优消费与最优目标函数分别是；投资前则是：i =r(a+F(h))，。

（二）市场存在债券类与流动性风险类资产

该风险资产的价格变动与技术创新收益变动部分相关。投资者可以通过交易以上两类资产规避和对冲风险，则投资收益服从下列过程：

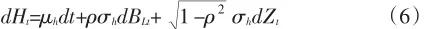
dAt=[rAt+α（tμL-r）-It]dt+αtσLdBLt（7）

定理2[18]在仅有债券类和流动性风险两类投资资产的非完备市场中，基于消费效用无差别的技术创新投资机会隐含价值F(h)满足如下微分方程及其条件：

F(-h)=-h-MFh(-h)=1（9）

其中-h为投资发生时刻的回报，投资后最优投资目标、最优消费与风险资产[18]分别是：

投资前最优投资目标、最优消费与风险资产分别是：

（三）投资资产分为具有流动性风险与非流动性风险且存在交易损失两大类

本文将投资资产分为具有流动性风险与非流动性风险两大类，且这两类资产价格变动与技术创新收益变动具有部分相关性，其中非流动性风险类考虑交易损失存在的情况。投资者不仅可通过购买的无风险资产规避投资风险，而且通过交易市场组合与有交易损失的股票规避技术创新收益风险。通过投资以下三类资产对冲投资风险：

债券类收益是在资金市场中以连续固定利率r指数增长，其收益服从如下过程：

dBt=rBtdt（10）

流动性风险类（比如S&P），其中μL，σL>0为常数，BLt是一维标准布朗运动且与Zt不相关，则其价格过程为：

非流动性风险类（比如新兴的市场投资证券组合），考虑到交易损失费用，其收益近似为市场收益的（1-θ）倍，其中μI，σI为常数，BIt是一维标准布朗运动且与BLt、Zt均不相关，则其市场收益的价格满足：

在以上非完备市场中，r，ρ1，ρ2，ρ3∈（0，1）是常数且，表示各风险资产价格与技术创新收益的相关系数，即数值越接近1，表示投资风险中各市场风险所占比例越高。则此时技术创新投资收益Ht如下：

dHt=μhdt+ρ1σhdZt+ρ2σhdBLt+ρ3σhdBIt（13）

设{Atϑt>0}代表投资者的资产L变化，αt，βt分别是t时刻投资者的流动性与非流动性风险资产分配。则其变化过程：

dAt=[rAt+αt(μL-r)+βt(1-θ)μI-rβt-It]dt+αtσLdBLt+ βt(1-θ)σIdBIt（14）

1.投资发生后的最优问题。假设V0(a)代表在投资发生后投资者的最优目标函数：

其中，At如（14）所示，且条件期望的初始资产A0=a。为便于计算，采用β=r，r是无风险利率。通过推导，得出Bellman方程如下：

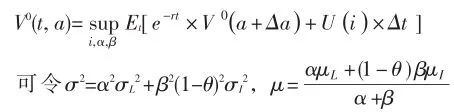
则由伊藤公式展开化简以上Bellman方程得到（15）。其中dBLtdBLt=ρdt，dtdt=0，dZtdBLt=dBLtdZt=0，ηL=分别代表各风险资产的市场价格。

2.投资发生前的最优问题。条件期望不仅仅与初始资产有关，还与投资预期带来的回报相关，同上述伊藤公式化简，最优问题获得的Bellman方程（16）如下：

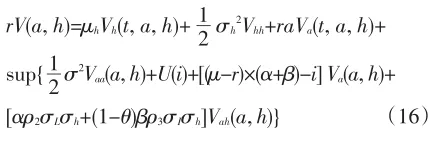
当h无穷小时，即回报为负无穷。作为理性投资人，投资者会选择不进行风险资产投资，则hl→im-∞V(a, h)=V0(a)；设τ为最优投资时刻且满足{τ|hτ= h͂}。从投资前后效用的关系入手分析，投资前比投资后多的投资机会应该有价值F(h)。从经济学角度来说，若该投资机会进行转让交易，其最低转让价格F(h)称为技术创新投资的隐含价值[19]。选择不同的投资组合，搭配不同的风险资产，其资产的隐含价值不同。则投资发生前的最优目标函数可设为：。

整理归纳以上讨论，得到下述定理：

定理3存在以上对冲交易的非完备市场中，基于消费效用无差别的技术创新投资机会的隐含价值F(x)满足如下微分方程及其条件：

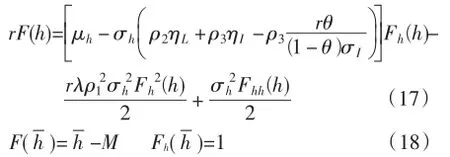
h为投资发生时刻的回报，投资后最优消费、最优目标函数分别是:

最优投资分配：

投资前最优目标函数、最优消费分别为：

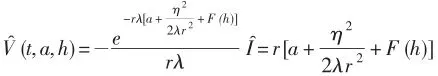
最优投资分配为：

证明：首先由Bellman（16）方程可得关于i，α，β的一阶条件：Ui(i)=V̂a(t,a, h)

其中，ηL=，分别代表流动性与非流动性风险资产的夏普比率，即流动性与非流动性风险的市场价格。将与代入（19）中可推导投资前的最优投资及投资分配。将V̂(a,h), Î,α̂,β̂代入化简投资前的最优目标函数即推导得证（17），其中（18）证明同定理1。

三、总结

通过最优消费、最优投资分配、最优目标函数以及投资前后的改变比较三个定理，可以推得如下内容：

首先，分别对比定理1与定理3在投资前后所得的最优消费，后者总比第一个多出消费部分η2/2rλ。这体现了该资产通过交易流动性与非流动性风险资产规避部分技术创新收益中存在的风险，多获得η2/2rλ消费。

其次，比较定理3投资前后由流动性与非流动性风险组成的最优投资分配组合，投资前比投资后分别多两项。这既与风险资产价格与技术创新收益的相关系数有关，也与风险资产相对无风险资产波动有关。随着ρ2，ρ3的增大而分别增大卖空流动性与非流动性风险资产的交易。受交易损失的影响，非流动性风险的卖空交易会随θ增大而增加。另外，投资前具有与技术创新本质风险ρiσh（i=2，3）相关的项，而投资后的分配则没有，说明决策者需要利用风险资产交易对冲部分市场风险。

第三，对比定理1与3所得的微分方程。Fh(h)项系数，后者因为进行风险资产交易对冲部分市场风险，减少了。受交易损失的影响，交易非流动风险资产对市场风险对冲作用减弱。而余下不能规避的市场风险部分即为本质风险，该部分具有的市场回报率为：，同样该部分随交易损失增加。项系数，后者比前者多减少了倍的，即本质风险贴水[20]，既受投资者对风险的厌恶系数λ影响，也受本质风险部分波动率的影响。由方程条件可知：最优投资触发水平随着F(h)递减，投资者对风险的厌恶系数λ与本质风险部分波动率和最优投资触发水平负相关。而传统实物期权[20]的最优投资触发水平不仅未考虑投资者的风险厌恶系数，而且会随着风险波动率增加而增大。

第四，对比定理2与定理3的最优目标函数、消费、投资分配与隐含价值，考虑当市场交易中增加一类具有交易损失的非流动性资产而引发的主要变化。一方面体现在η2的表达式，由单一的η2=细化为流动性风险资产的夏普比率（市场价格）η2L和与非流动性风险资产的夏普比率（市场价格）、交易损失及波动相关的两部分。另一方面则体现在将风险资产的对冲交易细化为流动性和具有交易损失的非流动性两类，投资后最优投资分配由单一的细化为分别与流动性和非流动性相关的两部分：和。而投资前同样由单一的细化为两部分：

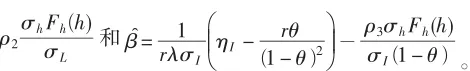
四、结论

本文首先阐述仅有债券类、仅有债券类与流动性风险类资产的投资对冲模型。由于技术创新投资的不确定性，从企业角度通过对冲间接推导最优投资回报、投资时间与投资分配。在非完备市场中，技术创新具有不确定性风险，通过流动性风险投资对冲风险，流动性与非流动性风险对冲并存，且由于非流动性较流动的差异，考虑了交易损失的存在。当市场中存在三类可投资资本：债券类、流动性风险类、存在交易损失的非流动性风险类，建立投资对冲模型，在理论上推导出相对简约的定理公式，一定程度上可为企业投资提供参考。鉴于行业规则与数据收集的真实性，未作数据代入。企业可以通过获取对应行业的基本收益回报水平μ与波动σ，流动性与非流动性及债券类的资产价格与项目收益的相关系数ρ1，ρ2，ρ3，各风险资产的市场价格η与风险厌恶系数λ、无风险利率r等相关数据，参照定理公式进行投资决策参考。

对比以上三种模型，讨论结果表明：

第一，通过交易流动性与非流动性风险资产，可对冲部分技术创新收益中存在的风险，多获得η2/2rλ消费。第二，风险厌恶型投资者的本质风险部分波动率ρ12σh2与最优投资触发水平负相关。这与传统投资定价结论相反[21]。第三，由于交易损失的影响，交易非流动风险资产对市场风险对冲作用减弱；而非流动性风险的卖空交易则与θ正相关。第四，增加一类具有交易损失的非流动性资产引发的变化，主要体现在η2和最优投资分配分别细化为两部分。

此外，技术创新投资交易区别于其他投资交易，在于其完善的评价体系。技术创新成果要有公认的度量衡，构建科学的创新成果评价体系，不仅有利于科学诊断和分析技术创新成果转化的障碍和前景，更有利于提振投资者信心，降低投资风险，确保投资收益。

参考文献:

［1］约瑟夫·熊彼特.经济发展理论[M].波士顿:哈佛大学出版社, 1926.

［2］Scherer F M. Research and Development Resource Allocation under Rivalry[J]. Quarterly Journal of Economics, 1967, 71(3).

［3］Scherer F M. Industrial Market Structure and Economics Performance[M]. Chicago: Rand McNally, 1980.

［4］Barzel Y. Optimal Timing of Innovations[J]. Review of Economic and Statistcs, 1968, 50(3).

［5］Loury G C. Market Structure and Innovation[J]. Quarterly Journal of Economics, 1979, 93(3).

［6］Lee T, Wild L L. Market Structure and Innovation: A Reformulation[J]. Quarterly Journal of Economics, 1980, 94(2).

［7］Reinganum J F. The Timing of Innovation: Research, Development and Diffusion[M]. North-Holland: Elsevier Science Publishers B. V, 1989.

［8］吴贵生.技术创新管理[M].北京:清华大学出版社, 2000.

［9］Dixit A K, Pindyck R S. Investment under Uncertainty[M]. NJ: Princeton University Press, 1994.

［10］Myers S C. Determinants of Corporate Borrowing[J]. Journal of Financial Economics, 1977, 10(1).

［11］Ross S A. A Simple Approach to the Valuation of Risky Income Streams[J]. Journal for Business, 1978, 5(3).

［12］Brennan M J, Schwartz E S. Evaluating Natural Resource Investments[J]. Journal of Business, 1985, 58(2).

［13］McDonald R, Siegel D R. The Value of Waiting to Invest[J]. Quarterly Journal of Economics,1986, 101(4).

［14］Zhaojun Yang, Hai Zhang. Optimal Capital Structure with an Equity-for-guarantee Swap[J]. Economics Letters, 2013(2).

［15］Follmer H, Schweizer M. Hedging of Contingent Claims under Incomplete Information[J]. Applied Stochastics Analysis, 1991(5).

［16］Choulli T, Stricker C. Minimal Entropy-hellinger Martingale Measure in Incomplete Markets[J]. Mathematical Finance, 2005, 15(3).

［17］R C Merton. Optimum Consumption and Portfolio Rules in a Continuous Time Model[J]. Journal of Economic Theory, 1971, 3(4).

［18］Yingcong Lan, Neng Wang, Jinqiang Yang. The Economics of Hedge Funds[J]. Journal of Financial Economics, 2013(2).

［19］Dixit A, Pindyck R. Investment under Uncertainty[M]. NJ: Prince⁃ton University Press, 1994.

［20］Miao J J, Wang N. Investment, Consumption and Hedging under Incomplete Markets[J].Journalof Financial Economics,2007,86(3).

［21］Stewart C M. Determinants of Corporate Borrowing[J]. Journal of Financial Economics, 1977, 5(2).

作者简介：张蕊家（1989-），女，宁波大学理学院硕士研究生，研究方向为金融数学。

基金项目：国家自然科学基金项目“调和分析及在偏微分方程中若干交叉问题的研究”（11171306）；浙江省自然科学基金项目“金融期权模型和分形随机方程的若干问题研究”（LY12A01024）

收稿日期：2015-02-04

文章编号：1672-3805(2015)02-0030-06

文献标识码：A

中图分类号：F830.59