二种求算晶体平面间距d(hkl)的数学方法*

于峰 温祖标

(江西师范大学化学化工学院 江西南昌 330022)

学生园地

二种求算晶体平面间距d(hkl)的数学方法*

于峰 温祖标**

(江西师范大学化学化工学院 江西南昌 330022)

用数学方法推导出结构化学晶体学中晶面间距的一般通式，并在此基础上推导出其他晶系的晶面间距(d(hkl)) 的计算表达式。

结构化学 数学方法 平面间距 晶胞参数 晶面指标

在高等学校的结构化学[1]教材中，对于晶体平面间距几乎都是仅给出了最后的计算公式，而没有给出严格的数学推导过程，这对于教师和学生而言，自然增加了相应的教与学的难度。广西师范学院范建春等[2]运用解析几何的思想来建立数学模型，并进行分析、推导、演算，推导了晶体二面间距，本文除了运用解析几何的方法还结合了空间平面方程，以及两向量的向量积和三阶行列式的展开等计算方法，使得在解析的过程中避免了对一些情况的分类讨论，同时也使得计算量大大减少，成功地推导出一般晶体的平面间距通式，并在此基础上推导出其他6种晶系的平面间距表达式。

不同种类的晶系，其空间构型也不同，其中最具有一般代表性的晶系为三斜晶系；而同种晶系由于划分点阵方法不同导致晶面间距也不同。因此，引入了晶面指标(hkl)，当平面指标确立之后，则平面间距也随之确定。

1 建立数学模型

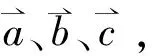
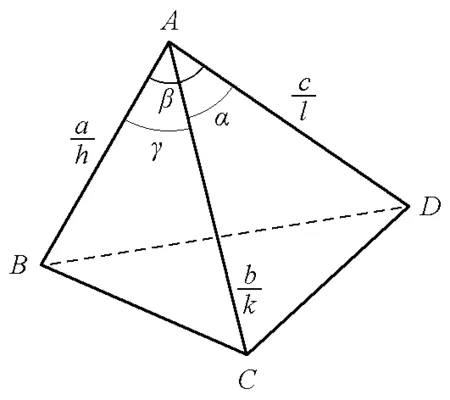
图1 晶体二面间距的示意图

对于指标为(hkl)的晶体，晶面两个平面间距离即等于原点到最近晶面的距离d(hkl)。这时存在如下关系:

2 d(hkl)的求解

2.1 建立空间直角坐标系

坐标设置自洽，符合数学模型。

图2 晶体二面间距的空间直角坐标系模型

2.2 求d(hkl)2.2.1 方法一

在ΔABD和ΔABC中，根据余弦定理,有:

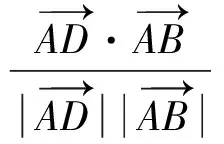
(1)

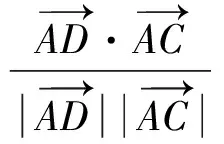
(2)

由式(1)和式(2)两式可得：

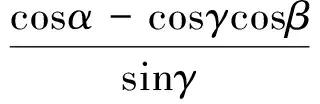
(3)

根据VD-ABC=VA-BCD,有：

① 求VD-ABC

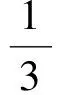
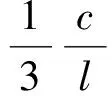
(4)

② 求VA-BCD

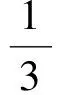
其中d(hkl)为晶面间距。

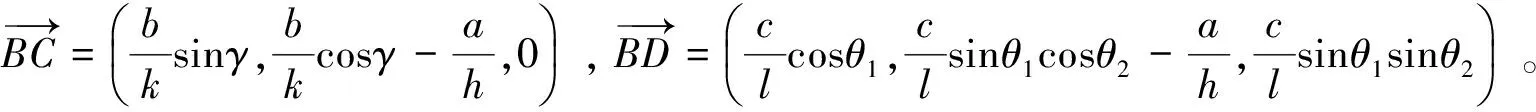
(5)

其中

i，j，k分别为x，y，z轴方向的单位向量[3-4]，则有：

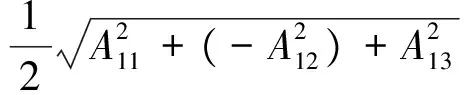
(6)

由式(1)、式(3)、式(6)可消去θ1、θ2，得：

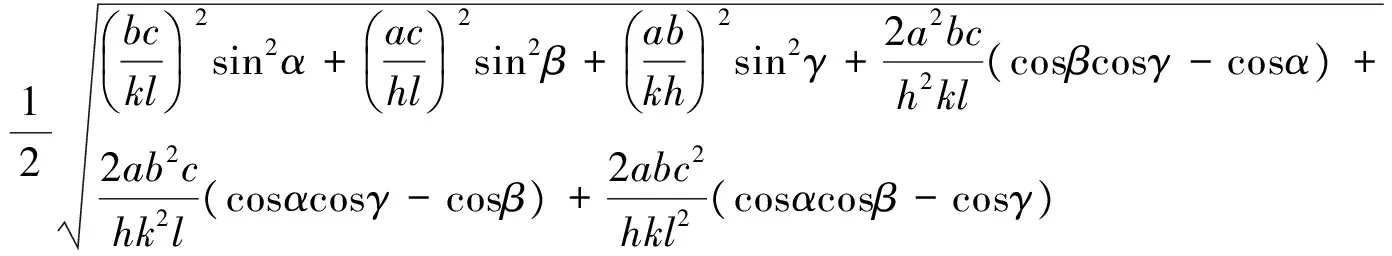
(7)

联立式(1)、式(3)、式(4)、式(5)、式(7)可得：

(8)

式(8)即晶面间距的计算公式。

2.2.2 方法二

化简可得:

则有：

(9)

3 不同晶系晶面间距d(hkl)的计算公式

根据不同晶系晶胞的特征参数，结合晶面间距的计算通式，可推导出相应的计算表达式。不同晶系晶面间距d(hkl)的计算公式列于表1。

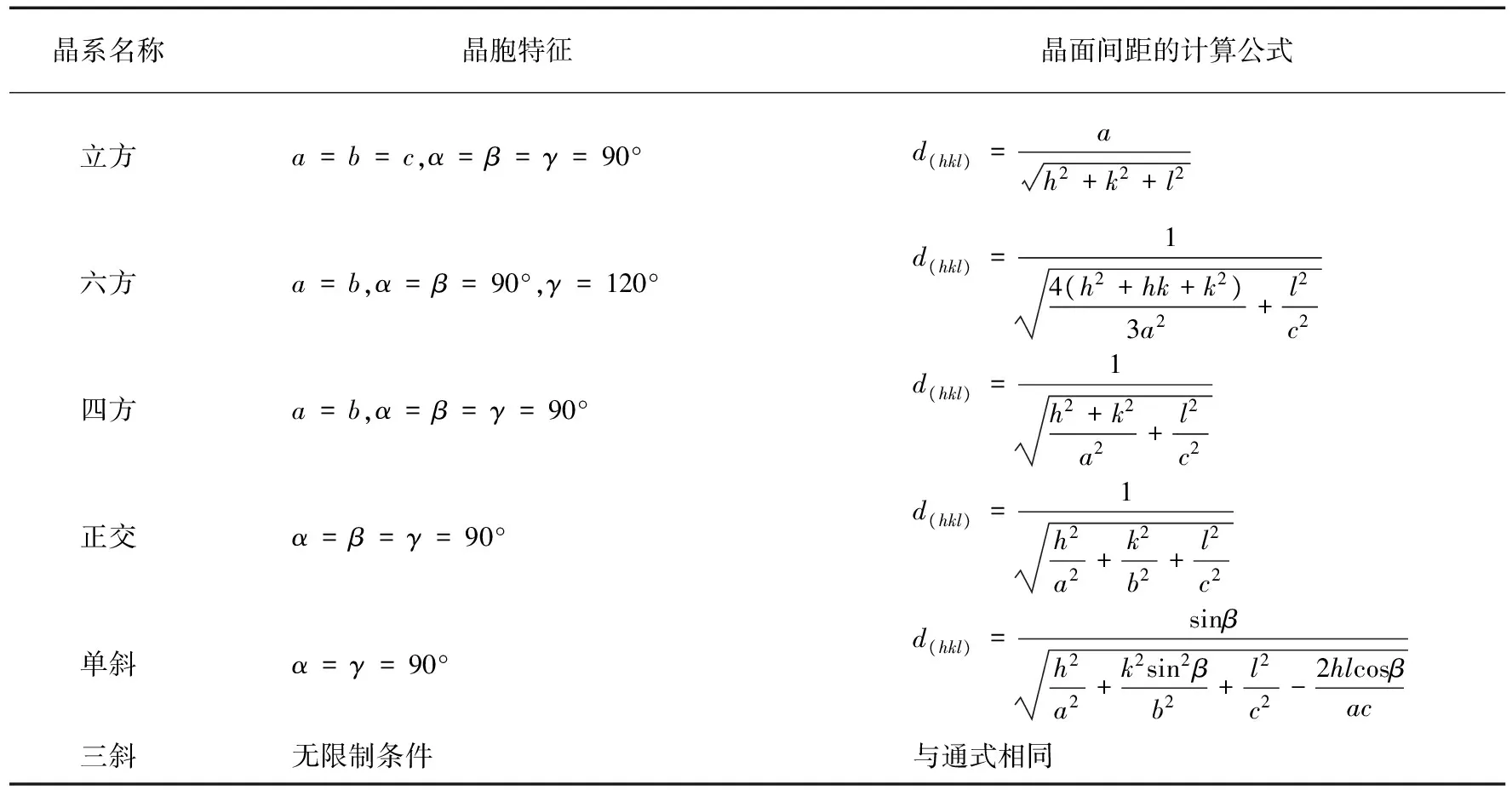
表1 不同晶系晶面间距d(hkl)的计算公式

[1] 周公度,段连运.结构化学基础.第3版.北京:北京大学出版社,2002

[2] 范建春,李丽琳,陈超球.广西师范学院学报,1999,16(1):92

[3] 钱逸泰.结晶化学导论.第3版.合肥:中国科学技术大学出版社,2005

[4] 同济大学数学系.高等数学.第6版.北京:高等教育出版社,2007

[5] 居余马.线性代数.第2版.北京:清华大学出版社,2002

TwoMathematicalSolutionstotheCrystalPlaneDistance*

Yu Feng Wen Zubiao* *

(CollegeofChemistryandChemicalEngineer,JiangxiNormalUniversity,Nanchang330022,Jiangxi,China)

A universal formula of crystal plane distance (d(hkl)) was obtained by using two different mathematical methods, and the formulaed(hkl)for other lattice systems were deduced based on the proposed method.

Structure chemistry; Mathematical method; Crystal plane distance; Space unit parameter; Indices of crystal face

10.3866/pku.DXHX20150486

博士启动基金(No.201061002)

**通讯联系人,E-mail:zbwen@jxnu.edu.cn

O6；G64