复杂氧化还原滴定曲线方程的Origin解析和曲线绘制*

孙晓波 王进平

(青岛农业大学化学与药学院 山东青岛 266109)

复杂氧化还原滴定曲线方程的Origin解析和曲线绘制*

孙晓波 王进平**

(青岛农业大学化学与药学院 山东青岛 266109)

本文首先利用物料平衡和林邦副反应思想分别推导出n1=n2和n1≠n2两种情况时的氧化还原滴定曲线方程，然后应用Origin软件对所推导的不同曲线方程进行解析，建立起以溶液电势E为因变量，滴定分数a为自变量的函数关系，并绘制其滴定曲线。

氧化还原滴定 滴定曲线 Origin

氧化还原滴定是化学分析的重要组成部分，而氧化还原滴定曲线的绘制对于理解氧化还原滴定的原理和过程具有重要作用[1]。已有文献利用物料平衡和林邦副反应思想分别推导出统一的氧化还原滴定曲线方程[2-4]，但鲜有文献对曲线方程进行解析，建立起以溶液电势为因变量，滴定分数为自变量的函数关系，从而绘制滴定曲线。即使有文献利用滴定曲线方程绘制滴定曲线，也主要集中在n1=n2的情况[5]。由于n1≠n2时，根据物料平衡推导出的氧化还原滴定曲线方程是一元多次方程，解析非常困难。虽然利用林邦副反应思想很容易建立起金属离子浓度与滴定分数的一元二次方程，但是由于滴定过程中离子浓度变化的复杂性，很难建立起统一的以溶液电势为因变量，滴定分数为自变量的函数关系。

本文以Ce4++Fe2+= Ce3++Fe3+及2Fe3++Sn2+=2Fe2++Sn4+为例，利用OriginPro8.5软件，根据物料平衡和林邦副反应思想，分别推导出n1=n2和n1≠n2两种情况时的氧化还原滴定曲线方程，同时建立起以溶液电势为因变量，滴定分数为自变量的函数关系，并绘制它们的滴定曲线。

1 n1=n2时的氧化还原滴定

1.1 物料平衡法

1.1.1 滴定曲线方程的推导

由文献[1]，根据物料平衡，氧化还原滴定曲线方程可以推导为：

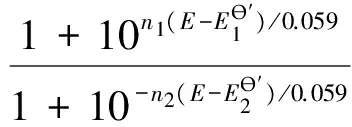
其中a为滴定分数，E为溶液电势。

当n1=n2时，滴定曲线方程可变换为：

设10nE/0.059=x,则上式变为：

方程解为：

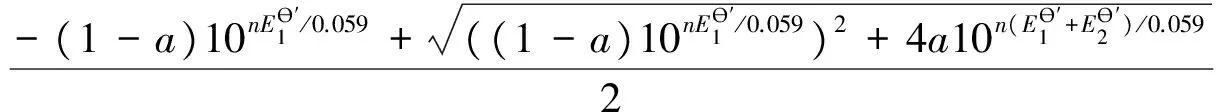
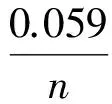
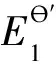
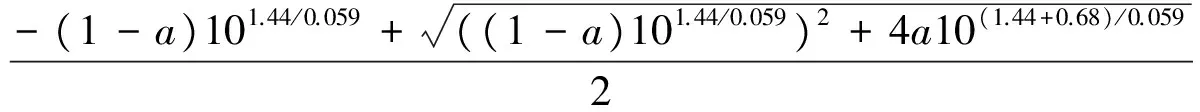
E=0.059lgx

由上述一元二次方程的解及x与溶液电势E的对数关系，可以建立起E为因变量，a为自变量的函数关系。

1.1.2 Origin软件解析曲线方程并绘制滴定曲线

在OriginPro8.5的worksheet中设Col(A)=a, 滴定分数a以0.001为步长，在0.000到2.000之间取值。

利用Set Column Values功能赋值：

-(1-a)101.44/0.059的值为：

Col(B)= (Col(A)-1)*10^(1.44/0.059)

((1-a)101.44/0.059)2+4a10(1.44+0.68)/0.059的值为：

Col(C)=sqrt(Col(B)^2+4*Col(A)*10^((1.44+0.68)/0.059))

Col(D)=(Col(B)+Col(C))/2

溶液的电势E为：

Col(E)=0.059*log(Col(D))

再利用worksheet中的set as功能，设Col(A)为x轴，Col(E)为y轴，利用OriginPro8.5的plot功能绘制Ce4+滴定Fe2+的滴定曲线如图1。由图1可以看出滴定的突跃范围为0.86～1.27V，与使用能斯特公式推导出的滴定突跃范围一致[1]。

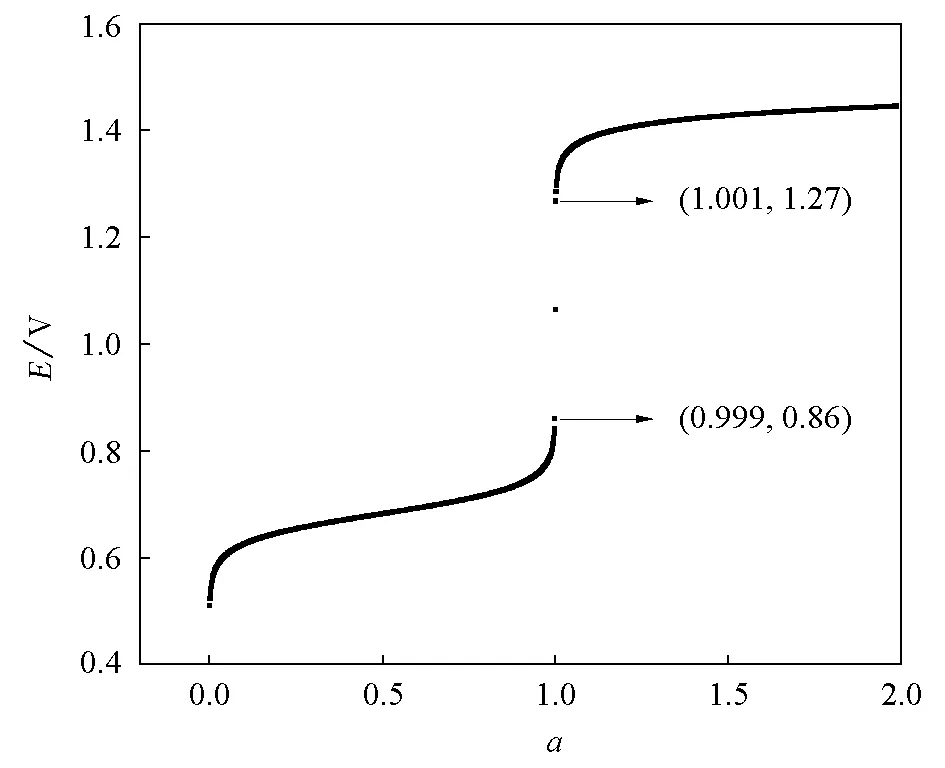
图1 物料平衡法推导并绘制的Ce4+滴定Fe2+的滴定曲线

1.2 林邦副反应思想

1.2.1 滴定曲线方程的推导

对于氧化还原反应Ce4++Fe2+=Ce3++Fe3+，采用林邦副反应思想，把一个半反应看作是另一个半反应的副反应。

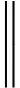
主反应常数为：

Kt=10EӨ(Ce4+/Ce3+)/0.059

不考虑副反应时，滴定曲线方程为：

Kt[Ce4+]2+(Ktc(Ce4+)(a-1)+1)[Ce4+]-c(Ce4+)=0

考虑副反应时，有：

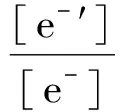
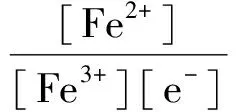
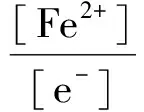
αe=1+KFe[Fe3+]

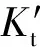
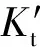
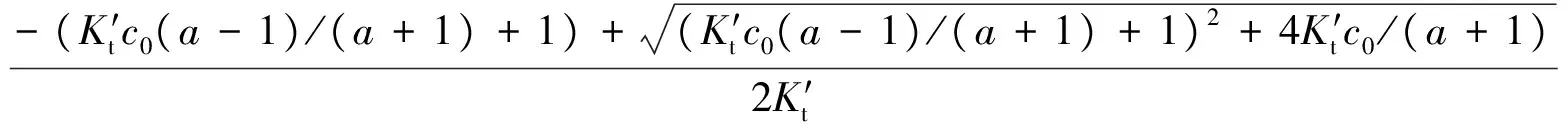
通过以上方程推导和解析，可以建立以金属离子浓度[Ce4+]为因变量，滴定分数a为自变量的函数关系。

1.2.2 Origin软件解析曲线方程并绘制滴定曲线

在OriginPro8.5的worksheet中，设Col(A)=a, 滴定分数a以0.001为步长，在0.000到2.000之间取值。且在本文中c0均为0.1000mol/L。

Col(B)=10^(1.44/0.059)/(1+(10^(0.68/0.059))*0.1*Col(A)/(1+Col(A)))

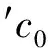
Col(C)=1+Col(B)*0.1*(Col(A)-1)/(Col(A)+1)

[Ce4+]为：

Col(D)=(-Col(C)+sqrt(Col(C)^2+4*Col(B)*0.1/(Col(A)+1)))/(2*Col(B))

当Fe2+滴定Ce4+时，溶液中的电势E为：

Col(E)=1.44+0.059*log(Col(D)/(0.1*Col(A)/(1+Col(A))-Col(D)))

绘制的Fe2+滴定Ce4+的氧化还原滴定曲线如图2。

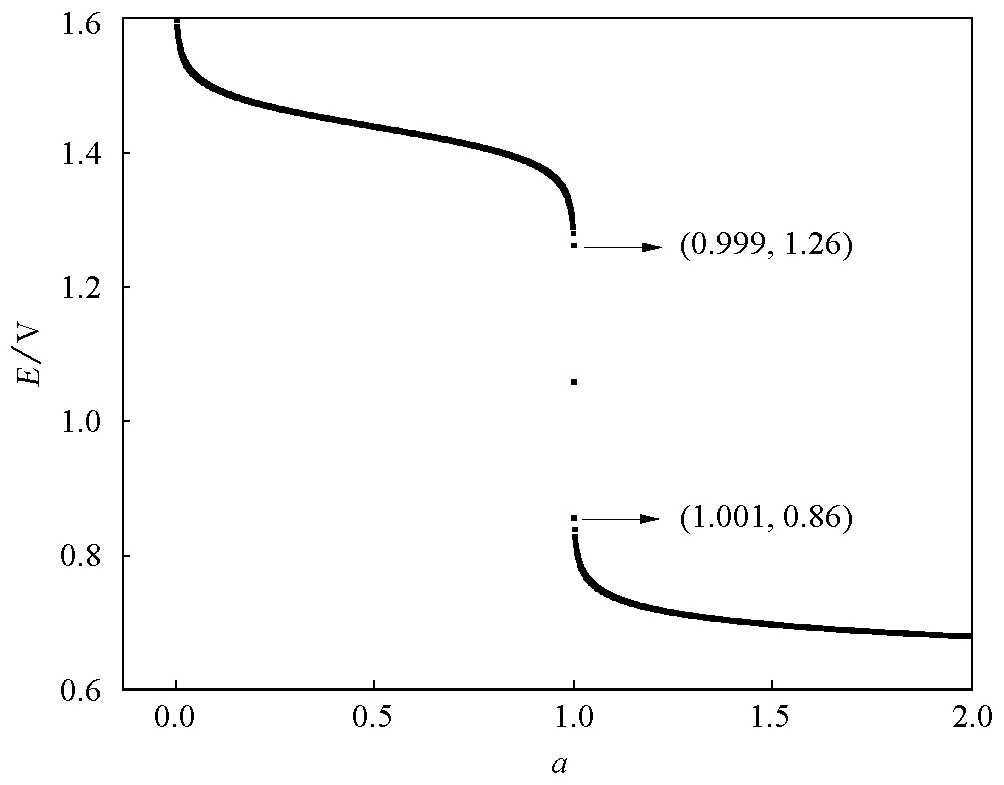
图2 林邦副反应法推导并绘制的Fe2+滴定Ce4+的滴定曲线

当Ce4+滴定Fe2+时，溶液中的电势E为：

Col(F)=0.68+0.059*log((0.1*Col(A)/(1+Col(A))-Col(D))/Col(D))

绘制的Ce4+滴定Fe2+的氧化还原滴定曲线如图3。

对物料平衡法和林邦副反应法所得滴定曲线进行对比发现，两种方法所绘制Ce4+滴定Fe2+的滴定曲线几乎完全重合，从曲线读出的滴定突跃范围与能斯特公式推导出的突跃范围一致[1]。

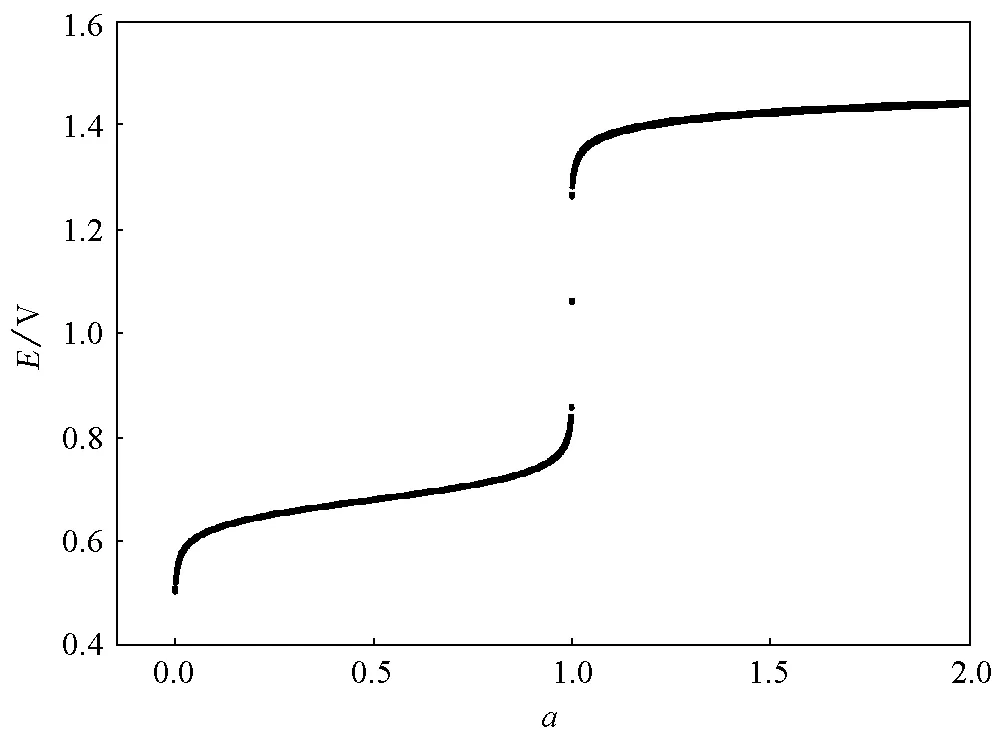
图3 物料平衡法和林邦副反应法推导并绘制的Ce4+滴定Fe2+的滴定曲线

2 n1≠n2时的氧化还原滴定

2.1 由物料平衡推导出的氧化还原滴定曲线方程

以氧化还原滴定2Fe3++Sn2+=2Fe2++Sn4+为例, 根据物料平衡，其滴定曲线方程为[1]：

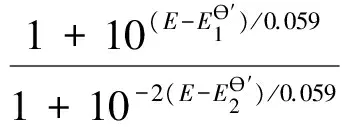
可以变换为：

设：10E/0.059=x,则上式变为：

上述方程为一元三次方程，经过Origin解析，难以建立起以电势E为因变量，滴定分数a为自变量的关系，故难以利用Origin绘制滴定曲线。

2.2 林邦副反应思想

2.2.1 Sn2+滴定Fe3+的滴定曲线方程推导

在1mol·L-1HCl介质中，有：

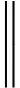
主反应常数为：

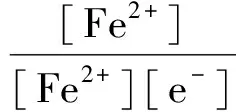
若不考虑副反应，则滴定曲线方程为：

Kt[Fe3+]2+(Ktc(Fe3+)(a-1)+1)[Fe3+]-c(Fe3+)=0

若考虑副反应，有：

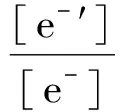
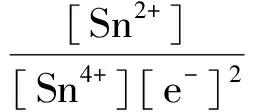
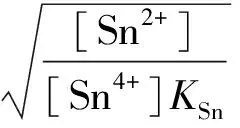
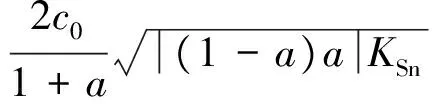
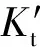
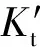
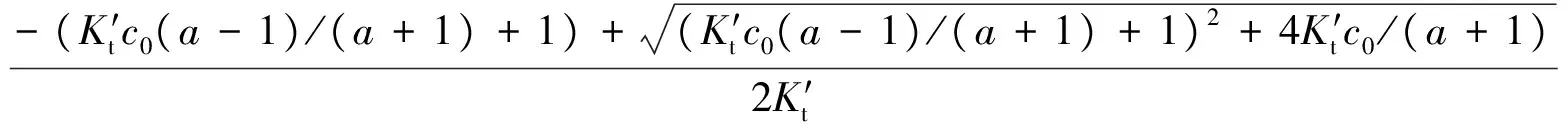
通过对以上方程的推导和解析，可以建立以[Fe3+]为因变量，滴定分数a为自变量的函数关系。

2.2.2 Origin软件解析曲线方程并绘制Sn2+滴定Fe3+的滴定曲线。

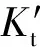
[Fe3+]为：

Col(D)=(-Col(C)+sqrt(Col(C)^2+4*Col(B)*0.1/(Col(A)+1)))/(2*Col(B))

溶液中的电势E为：

Col(E)=0.70+0.059*log(Col(D)/(0.1*Col(A)/(1+Col(A))-Col(D)))

绘制的Sn2+滴定Fe3+的氧化还原滴定曲线如图4。

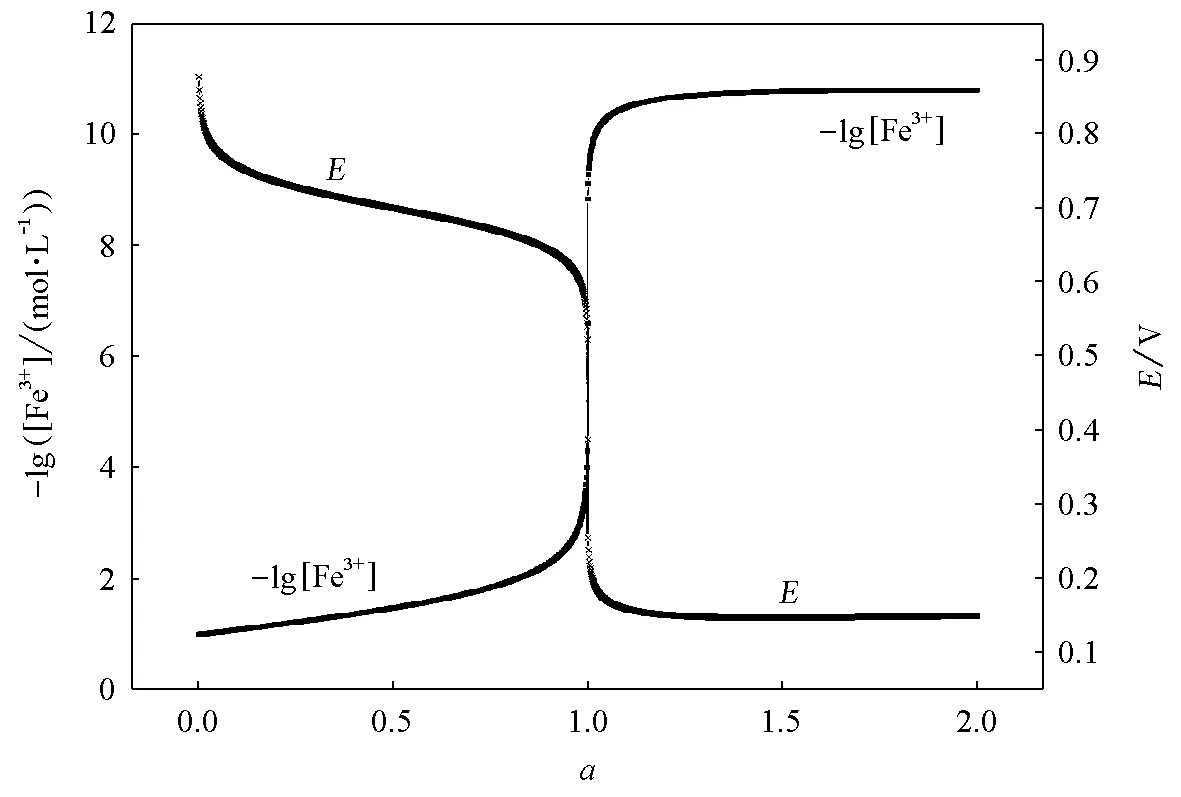
图4 用林邦副反应法推导并绘制Sn2+滴定Fe3+的滴定曲线

2.2.3 Fe3+滴定Sn2+的滴定曲线方程推导

在1mol·L-1HCl介质中，有：

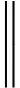
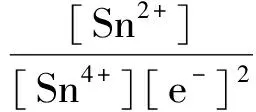
若不考虑副反应，滴定曲线方程为：

Kt[Sn4+]2+(Ktc(Sn4+)(a-1)+1)[Sn4+]-c(Sn4+)=0

若考虑副反应，有：

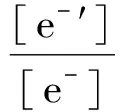
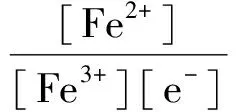
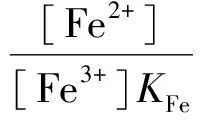
αe=1+[Fe3+]KFe

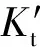
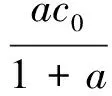
当求滴定过程中[Sn2+]时，滴定曲线方程可以写为：

通过对以上方程推导和解析，可以建立以[Sn2+]为因变量，滴定分数a为自变量的函数关系。

2.2.4 Origin软件解析曲线方程并绘制Fe3+滴定Sn2+的滴定曲线

同1.2.2，Col(A)放置滴定分数a的数值，a以0.001为步长，在0.000到2.000之间取值。

[Sn2+]为：

Col(D)=(-Col(C)+sqrt(Col(C)^2+4*Col(B)*0.1/(Col(A)+1)))/(2*Col(B))

溶液中的电势E为：

Col(E)= 0.14+0.059*0.5*log((0.1*Col(A)/(1+Col(A))-Col(D))/(Col(D)))

绘制的Fe3+滴定Sn2+的氧化还原滴定曲线如图5。由图5读出的滴定突跃范围(0.23～0.57V)与能斯特公式推导出的突跃范围一致[1]。这进一步表明，此方法可以很好地绘制包括n1≠n2在内的氧化还原滴定曲线。

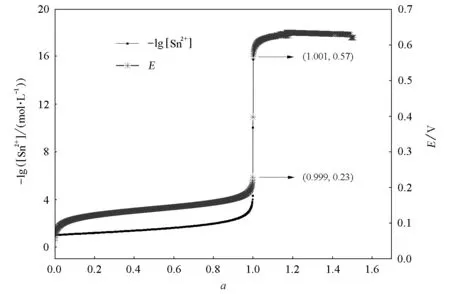
图5 用林邦副反应法推导并绘制的Fe3+滴定Sn2+的滴定曲线

[1] 武汉大学.分析化学.第5版.北京:高等教育出版社,2006

[2] 乔成立,李文新,马秀芳.高师理科学刊,2008,28(5):78

[3] 孟凡昌,杨代菱.大学化学,2001,16(2):31

[4] 徐卫河,牛安妮,李亚萍.郑州大学学报(自然科学版),28(2):101

[5] 何妮,吕瑞芳,周颖华.四川教育学院学报,2010,26(9):110

ApplicationofOriginSoftwaretoRedoxTitrationCurvePlotting*

Sun Xiaobo Wang Jinping* *

(CollegeofChemistryandPharmaceuticalSciences,QingdaoAgriculturalUniversity,Qingdao266109,Shandong,China)

In this paper, redox titration functions were derived by mass balance theory and Ringbom′s side reaction approach. Origin software was used to solve the functions and plot redox titration curves.

Redox titration; Titration curve; Origin

10.3866/pku.DXHX20150478

山东省高等学校精品课程(No.2013BK205);山东省高等教育应用型人才培养特色名校建设项目

**通讯联系人，E-mail:jpwang@qau.edu.cn

O6；G64