Debye-Hückel离子互吸理论的改进*

刘国杰 黑恩成

(华东理工大学化学系 上海 200237)

Debye-Hückel离子互吸理论的改进*

刘国杰 黑恩成

(华东理工大学化学系 上海 200237)

根据强电解质水溶液形成的热力学设想，修正了Debye-Hückel离子互吸理论，检验结果表明，它能满意地关联各种价型的强电解质水溶液的离子平均活度因子，使适用的浓度范围扩大到了6mol·kg-1。

Debye-Hückel离子互吸理论 强电解质水溶液 离子平均活度因子

在电化学的热力学研究中，电解质溶液的离子平均活度因子是不可缺少的，虽然有许多测定的方法，但要在理论上计算它，迄今依然十分困难。最成功的理论莫过于Debye-Hückel离子互吸理论，几乎在所有物理化学教科书上，都对其有所介绍。然而，该理论仅适用于质量摩尔浓度不超过0.1mol·kg-1的强电解质稀溶液。虽然Pitzer[1]用半经验方法发展了一个强电解质水溶液离子平均活度因子方程，使适用范围扩大到了6mol·kg-1左右，但该方程中含有3个可调参数，而且需要较高深的统计力学知识，并非一般物理化学教科书所能介绍。本文试图通过一种简单的热力学方法来修正Debye-Hückel离子互吸理论，期待能够达到同样的目的。

1 离子互吸理论简述

Debye和Hückel认为，在电解质溶液中，有两个相互制约的因素决定着离子的运动。一是离子的热运动，它要使正、负离子随机地分布；另一是正、负离子间的静电作用，它要使离子规则地排列。正是这两个因素决定了强电解质溶液具有这样的结构：每一个正离子犹如被一层离子氛所包围，统计地说，这个离子氛是带负电的，且其电荷值与正离子的相等。同样，每一个负离子的周围也有一个离子氛，它统计地带有正电，电荷值与负离子的相等。故每个离子既是某个离子氛的中心离子，又是其他离子的离子氛中的一员。这个结构处在动态平衡之中。

按照上述模型，Debye和Hückel作了如下5点假设[2]：

① 电解质在溶液中是完全电离的；

② 离子可视为带电的刚球，它的电场是球形对称的；

③ 离子间只存在库仑力，其他作用可以忽略不计；

④ 离子间的相互作用能远小于其热运动能；

⑤ 溶液的介电常数与纯溶剂的介电常数没有区别。

于是，由正、负离子的活度定义式，可得：

(1)

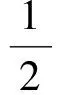
(2)

式中E为某个中心离子与其离子氛间的静电作用能，L为Avogadro常量，式中的1/2是为了避免重复计算。

Debye和Hückel根据静电场中离子的能量遵守Boltzmann分布定律和离子的电荷密度与电势间关系可由Poisson方程表示，解得了E的表示式，从而得到:

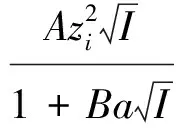
(3)

(4)

式(4)便是用离子互吸理论得到的正、负离子平均活度因子表示式。式中z+和z-分别为正、负离子的电荷数；a为正、负离子半径之和；I为离子强度，其定义式为：

(5)

式中A和B为两个仅与纯溶剂性质有关的参数，其中

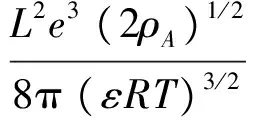
(6)

式中e为基本电荷，L为Avogadro常量，ρA为溶剂的密度，ε为介电常数。25℃时，对于电解质水溶液，A=1.171mol-1/2·kg1/2，B=0.3282×1010mol-1/2·kg1/2·m-1。

2 离子互吸理论的改进

按照热力学观点，强电解质水溶液的形成可设想由如下两步完成：

第Ⅰ步为水与电解质混合，变成体积可加的混合物；在这一步中设想电解质是以分子态存在于混合物中。第Ⅱ步为电解质分子在水中电离成正、负离子，从而变成摩尔体积为Vm的电解质水溶液。据此不难看出，Debye-Hückel离子互吸理论仅仅适用于其中的第Ⅱ步。

根据这个设想，可得强电解质水溶液的混合Gibbs自由能为：

ΔmixG=ΔG(Ⅰ)+ΔG(Ⅱ)

(7)

将式(7)等号两边同时减去理想混合物的混合Gibbs自由能，可得：

GE=GE(Ⅰ)+ΔG(Ⅱ)

(8)

若在T、p、n1保持不变的条件下，将式(8)对n2求偏导，则由热力学关系(∂GE/∂n2)T,p,n1=RTlnγ2和(∂ΔG/∂n2)T,p,n1=Δμ可得:

RTlnγ2=RTlnγ2(Ⅰ)+Δμj(Ⅱ)

(9)

式中γ2为水溶液中电解质的活度因子，γ2(Ⅰ)为第Ⅰ步混合物中分子态电解质的活度因子，Δμj(Ⅱ)为第Ⅱ步水溶液中电解质离子j的化学势与无限稀释时(理想稀溶液中)离子j的化学势之差。式(9)也可表示为:

lnγ±=lnγ2(Ⅰ)+lnγ±(Ⅱ)

(10)

式中代入了式(2)，即Δμj=RTlnγj。由于水溶液中强电解质离解出的正、负离子总是共存的，并且离子的活度因子可以正、负离子的平均活度因子表示，故式 (9)可表示成式(10)。再将式(4)代入式(10)，得：

(11)

由此可见，只要得到第Ⅰ步混合物中分子态电解质的活度因子表示式，便可求得改进后的强电解质水溶液的离子平均活度因子。

3 lnγ2(Ⅰ)表示式

鉴于第Ⅰ步不涉及离子，lnγ2(Ⅰ)可由非电解质溶液理论来解决。用类似于前文[3]的方法，第Ⅰ步的超额焓可表示为:

这里，需要假定混合物的内压力与组分的内压力间存在如下关系：

(13)

并令：

(14)

其中l12是一个修正几何平均假设的参数，引入这个参数是基于水与电解质的混合物是一个有缔合组分的系统，前文[3]所得的修正Scatchard-Hildebrand正规溶液理论是不适用的。将式(14)代入式(13)，则得：

λ2=(φ1λ1+φ2λ2)2-2φ1φ2λ1λ2l12

(15)

式中φ1=x1Vm,1/(x1Vm,1+x2Vm,2)和φ2=x2Vm,2/(x1Vm,1+x2Vm,2)分别为混合物中水和电解质的体积分数。

同样，混合物的m与组分的m1和m2间也需引入一个假定。为了简单起见，保留前文[3]中假定的形式，即：

m=φ1m1+φ2m2

(16)

这里应该指出，式中m1和m2已非它们纯态时的值。由于混合时水会解缔和电解质会水化，故m1和m2都只能说是两个表观值。

将式(15)和式(16)代入式(12)，经整理，得：

(17)

第Ⅰ步的超额熵则可由前文[4]得到的修正的无热溶液理论表示为：

SE(Ⅰ)=nRln(1-Λx1)-n1Rln(1-Λ)

(18)

式中Λ也是一个可调参数。因此，第Ⅰ步的超额Gibbs自由能为：

(19)

于是，由热力学关系RTlnγi=(∂GE/∂ni)T,p,nj≠i，不难得到，第Ⅰ步电解质的活度因子为：

(20)

将式(20)代入式(11)，得：

(21)

这就是本文得到的强电解质水溶液的离子平均活度因子方程。式中有3个参数，即α、β和Λ，它们是方程的3个可调参数。不难看到，当这些参数都等于0时，式(21)便变成式(4)。

4 式(21)的检验

图1～图3是对不同价型的若干强电解质水溶液的离子平均活度因子关联结果，它们的最高质量摩尔浓度达6mol·kg-1。

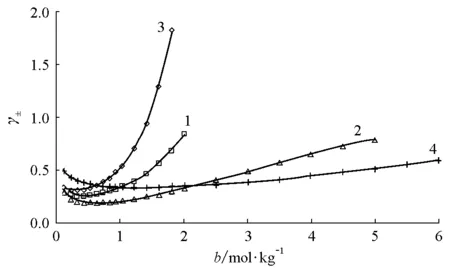
图1 离子平均活度因子与质量摩尔浓度的关系(298.15K) 1 CeCl3,2 Th(NO3)4,3 AlCl3,4 Ca(NO3)2,以上为实验值[5]；曲线为式(21)计算值

图2 离子平均活度因子与质量摩尔浓度的关系(298.15K) 1 CaCl2,2 MgCl2,3 Pb(ClO4)2,4 CaBr2,以上为实验值[5];曲线为式(21)计算值

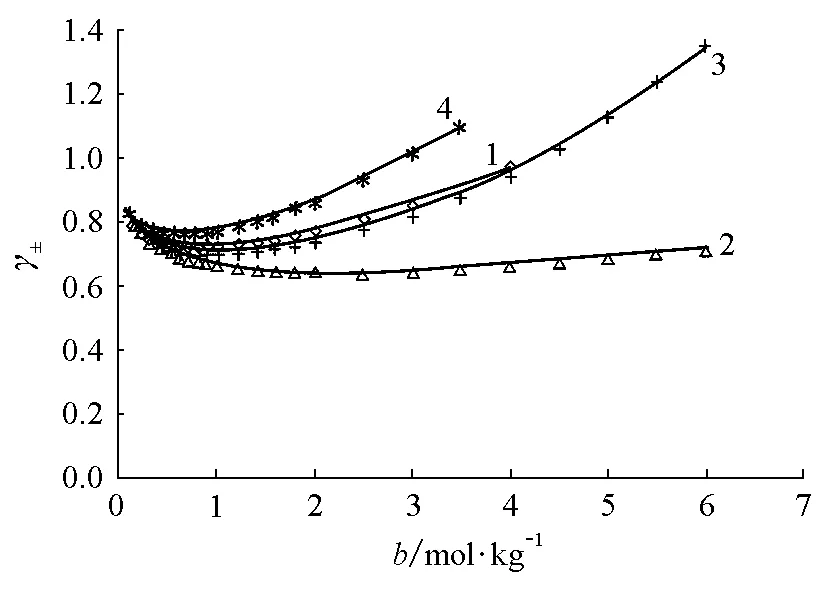
图3 离子平均活度因子与质量摩尔浓度的关系(298.15K) 1 NaBr,2 Na(ClO4),3 NaOH,4 NaI,以上为实验值[5];曲线为式(21)计算值

由图1～图3可见，对各种价型的强电解质水溶液，γ±计算值与实验值间的一致性是很满意的。表1列出了关联所得的α、β和Λ参数值，以及lnγ±计算的标准偏差σ，它的定义为：

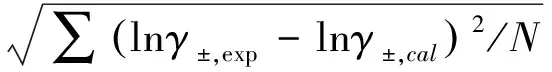
(22)

其中N为实验点数目。

表1中的a为正、负离子的半径之和，由于离子的水化，其值是不确定的，本工作没有考虑水化层厚度，就取正离子和负离子的晶体半径之和，其值取自文献[6]。

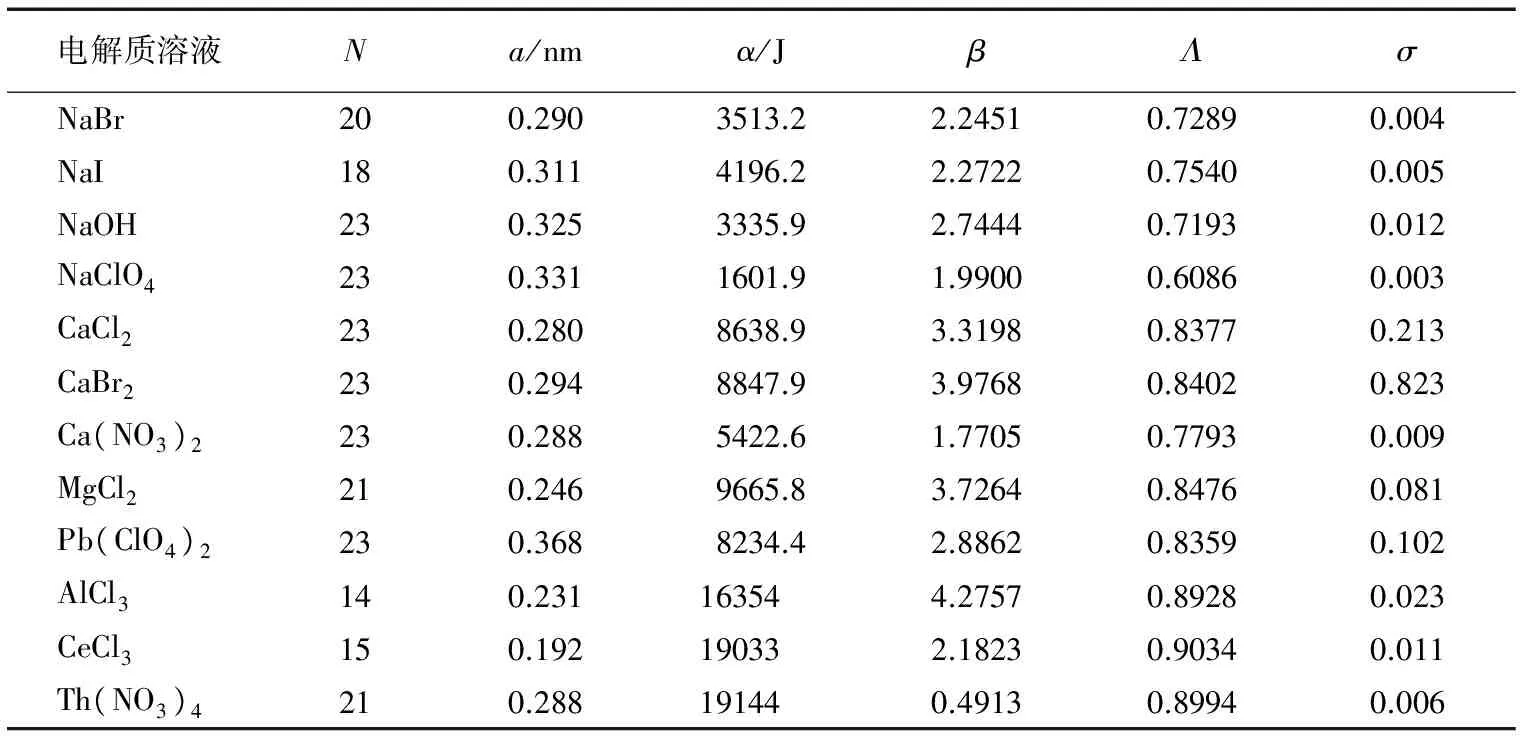
表1 298.15K时若干强电解质水溶液的离子平均活度因子计算结果及参数值

表1中CaBr2的标准偏差σ较大些，这是因为它的γ±值随浓度增高而迅速增大，浓度较高时，γ±值远比其他强电解质水溶液的大，在6mol·kg-1时，它的γ±值高达55.7(图2中没有画出)，这便使标准偏差σ要比其他强电解质水溶液大，为0.823。其实，如果用平均相对误差来表示，仅为2.2%。

由此可见，对于本工作得到的三参数关联式，虽然其3个参数为半经验的可调参数，但能满意地关联质量摩尔浓度小于6mol·kg-1的各种强电解质水溶液的离子平均活度因子，相比于原始的Debye-Hückel离子互吸理论，适用的浓度范围有了很大扩展。

[1] Pitzer K S.JPhysChem,1973,77:268

[2] 黄子卿.电解质溶液理论导论.修订版.北京:科学出版社,1983

[3] 刘国杰,黑恩成.大学化学,2007,22(5):59

[4] 黑恩成,刘国杰.大学化学,2008,23(1):67

[5] Robinson R A,Stokes R H.Electrolyte Solutions.2nd ed.London:Butterworths Scientific Publications,1959

[6] Marcus,Y.Introduction to Liquid State Chemistry.London:John Wiley & sons,1977

ModificationofDebye-HückelTheory*

Liu Guojie Hei Encheng

(SchoolofChemistry,EastChinaUniversityofScienceandTechnology,Shanghai200237,China)

Based on the thermodynamic properties of ions in solution, we modified the Debye-Hückel expression. The modified expression could be well correlated with the mean activity coefficients of different strong electrolyte aqueous solutions with various ionic charges, and the applicable concentration range is extended to 6mol·kg-1.

Debye-Hückel theory; Strong electrolyte aqueous solution; Mean activity coefficients

10.3866/pku.DXHX20150468

华东理工大学网络教育教改项目(No.WJY2014006);教育部教育质量工程建设项目(No.YJ0136102);国家精品资源共享课建设项目(No.YJ0125206)。

O6；G64