气体节流膨胀过程的热力学分析*

胡新根林娟娟

(温州大学化学与材料工程学院 浙江温州 325035)

气体节流膨胀过程的热力学分析*

胡新根**林娟娟

(温州大学化学与材料工程学院 浙江温州 325035)

探讨气体节流膨胀过程中的熵(S)的变化，指出任何气体的节流膨胀都是熵增过程，并且是不可逆的。在此基础上，讨论和总结了节流膨胀过程的全部热力学特征。

气体 节流膨胀 焦耳-汤姆逊效应 熵 热力学特征

气体节流膨胀(throttling expansion)是一种很重要的热力学过程[1]，在各种经典的物理化学、热物理或热力学教程中都占重要的位置[2-6]。在物理化学教学实践中，讲授好节流膨胀的有关内容对培养学生发现问题、分析问题和解决问题的能力具有重要意义。在国内，主流的物理化学教材[7-11]大多把这一内容安排在热力学第一定律的有关章节中，强调节流膨胀是一个等焓过程(isoenthalpic process)，实际气体发生节流膨胀后温度可能升高也可能降低，并引入焦耳-汤姆逊(温度)系数(Joule-Thomson coefficient，μJ-T=(∂T/∂p)H)来表征这一效应，然后进一步分析影响μJ-T大小的决定因素，见式(1)。

(1)

1 节流膨胀过程的熵变化

下面分析气体发生节流膨胀时系统和环境的熵(S)分别如何变化这个问题。

因为节流膨胀是在绝热(adiabatic)条件下发生的，即δQ系统=-δQ环境=0，所以环境的熵变为：

(2)

即节流膨胀时环境的熵保持不变。那么，系统(所研究的那部分气体)的熵会如何变化呢？

根据热力学第二定律的克劳修斯不等式(Clausius inequality)，对于在一个热力学系统中发生的任意过程(A→B)，有：

(3)

式中等号表示可逆过程，不等号表示不可逆过程。由于节流膨胀过程δQ系统=0，因此有：

(4)

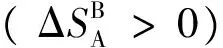
我们已经知道，气体节流膨胀是一个等焓、降压过程，即dH=0，dp<0。实际气体经节流膨胀后温度可能升高，也可能降低，也可能保持不变，这要视气体的种类和原始状态而定。我们常用焦耳-汤姆逊系数(μJ-T)来表征这一性质：

(5)

对于式(5)中的(a)、(b)、(c) 3种情况，虽然我们知道气体的温度是如何变化的，但还不清楚气体的熵S是如何变化的。为此，我们来探讨下面这个偏微分：

(6)

式中的系数τJ-T表示在等焓情况下，系统的熵S随压力p的变化率，下面将其称为焦耳-汤姆逊熵系数(Joule-Thomson entropic coefficient)。

如果根据热力学基本方程dH=TdS+Vdp，再令dH=0(因节流膨胀过程等焓)，则：

TdS+Vdp=0

(7)

即：

(8)

式(8)表明，在任何气体节流膨胀过程(dp<0)，系统的熵总是增加的(dS>0)，因此必然是一个不可逆过程(绝热系统熵增原理)，并且熵的变化与温度的变化不一定同调。由式(8)可得节流膨胀系统熵变的计算公式：

(9)

进一步可得焦耳-汤姆逊熵系数(τJ-T)与焦耳-汤姆逊(温度)系数(μJ-T)之间的关系：

(10)

即:

(11)

式(11)表明，在实际气体节流膨胀过程(dT≠0，μJ-T≠0)，系统的温度T随熵S的变化率(∂T/∂S)H等于μJ-T与τJ-T之比。当μJ-T与τJ-T异号时，T随S增大而降低；当μJ-T与τJ-T同号时，T随S增大而升高。

另外，由于节流膨胀过程是绝热的，环境的熵变为0(ΔS环境=0)，因此有：

ΔS隔离=ΔS系统+ΔS环境>0

(12)

由于整个隔离系统的熵变大于0，因此节流膨胀过程是不可逆的。

2 节流膨胀过程的其他热力学特征

在上述熵函数分析的基础上，我们对气体节流膨胀过程的其他热力学特征进行了系统的讨论和总结。

① 节流膨胀是绝热(Q=0)、等焓(ΔH=0)和压降(Δp<0)过程。理想气体节流膨胀时温度保持不变。实际气体节流膨胀后的温度变化有3种可能：降低(μJ-T>0)、不变(μJ-T=0)和升高(μJ-T<0)；温度变化的方向及幅度与实际操作条件有关，降低终态压力有利于提高变温幅度。

② 节流膨胀的功(W)和内能(热力学能，U)的变化为：

W=ΔU-Q=ΔU=ΔH-Δ(pV)=-Δ(pV)=pAVA-pBVB

(13)

该式说明，气体进行节流膨胀时，若消耗了内能(ΔU<0)，则必定完全用于对外作功(W<0，Δ(pV)>0)；若增加了内能(ΔU>0)，则是得到了环境对它所作的功(W>0，Δ(pV)<0)。这也可以从下式看出：

(14)

该式表明，在气体节流膨胀过程，内能变化与复合状态函数(pV)的变化密切相关。若Δ(pV)>0，则ΔU<0，即内能降低；若Δ(pV)<0，则ΔU>0，即内能增高；若Δ(pV)=0，则ΔU=0，即内能不变，如理想气体的情况。

另外，根据热力学基本方程dU=TdS-pdV，有：

(15)

式中υJ-T称为焦耳-汤姆逊体积系数。可见，节流膨胀过程中气体内能U是否与温度T同调变化，与TτJ-T和pυJ-T之差密切相关。

若是理想气体(pV=nRT)的节流膨胀，则因过程等焓(ΔH=0)且等温(ΔT=0)，故必定内能不变(ΔU=0)且不作功(W=0)。

③ Helmholtz自由能(A)的变化为：

ΔA=ΔU-Δ(TS)=W-Δ(TS)=-Δ(pV)-Δ(TS)=-Δ(pV+TS)

(16)

可见，节流膨胀过程气体的Helmholtz自由能的变化(ΔA)等于复合状态函数(pV+TS)变化的负值。若是理想气体，则：

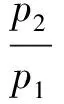
(17)

④ Gibbs自由能(G)的变化为：

ΔG=ΔH-Δ(TS)=-Δ(TS)

(18)

即气体节流膨胀过程Gibbs自由能的变化(ΔG)等于复合状态函数(TS)的变化。若是理想气体，则：

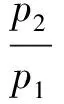
(19)

3 结论

通过以上分析和讨论可知，不论是实际气体还是理想气体，节流膨胀过程都是熵增的(ΔS>0)，与系统的温度T、压力p、焓H、内能U、Helmholtz自由能A、Gibbs自由能G等的变化不一定同调。在热力学第一定律和第二定律的教学实践中，若能充分利用气体节流膨胀这一典型热力学过程，开展探究式教学或案例教学，通过全面分析其热力学特征，弄清各热力学函数之间的联系，就可以让学生充分体验热力学研究方法的特点，从而激发学生对相关内容的学习热情，并取得理想的教学效果。

[1] Reif F.Fundamentals of Statistical and Thermal Physics.Boston:McGraw-Hill,1965

[2] Adamson A W.A Textbook of Physical Chemistry.New York:Academic Press,1973

[3] Castellan G W.Physical Chemistry.2nd ed.Massachusetts:Addison-Wesley,1971

[4] Roy B N.Fundamentals of Classical and Statistical Thermodynamics.New York:John Wiley & Sons,2002

[5] Moran M J,Shapiro H N.Fundamentals of Engineering Thermodynamics.5th ed.New York:John Wiley & Sons,2003

[6] Atkins P,Julio de P.Atkin′s Physical Chemistry.Oxford:Oxford University Press,2006

[7] 傅献彩,沈文霞,姚天扬,等.物理化学.第5版.高等教育出版社,2005

[8] 韩德刚,高执棣,高盘良.物理化学,第2版.高等教育出版社,2009

[9] 天津大学物理化学教研室.物理化学,第5版.高等教育出版社,2011

[10] 万洪文,詹正坤.物理化学.第2版.高等教育出版社,2010

[11] 胡英,吕瑞东,刘国杰,等.物理化学,第5版.高等教育出版社,2007

ThermodynamicAnalysisonThrottlingExpansionofGases*

Hu Xingen* *Lin Juanjuan

(CollegeofChemistryandMaterialsEngineering,WenzhouUniversity,Wenzhou325035,Zhejiang,China)

In this paper, the change of entropy function (S) in the process of gas throttling expansion has been explored. It has been pointed out that the entropy change associated with the throttling expansions of any gases is always positive, and that the process is irreversible. The total thermodynamic characteristics of throttling expansions have been systematically discussed and summarized. The content involved is of importance in the teaching practice for students to gain better insights into the characteristics of the irreversible process, the function of entropy and the principle of entropy increase, as well as the relationships among all thermodynamic functions.

Gas; Throttling expansion; Joule-Thomson coefficient; Entropy; Thermodynamic characteristics

10.3866/pku.DXHX20150474

浙江省精品课程建设项目

**通讯联系人，E-mail:hxgwzu@126.com

O6；G64