稀溶液中化学势的计算以及渗透压公式的推导*
2015-12-07陈飞武韦美菊叶亚平袁文霞
陈飞武韦美菊 叶亚平 袁文霞
(北京科技大学化学与生物工程学院 北京 100083)
稀溶液中化学势的计算以及渗透压公式的推导*
陈飞武**韦美菊 叶亚平 袁文霞
(北京科技大学化学与生物工程学院 北京 100083)
将溶液中某组分化学势的计算方式归纳为两种:(1)利用气液平衡时,溶液中某组分的化学势和气相中该组分的化学势相等这一关系来计算;(2)利用溶液中某组分化学势的全微分表达式直接积分来计算。在此基础上,给出了渗透压公式的一种新推导方式,并指出部分物理化学教材关于渗透压定义(Π=p2-p1)的不合理性以及推导渗透压时存在的不妥之处。
化学势 渗透压 溶液 化学势
1 问题的提出
稀溶液中溶剂的蒸气压下降、凝固点降低(析出固体纯溶剂)、沸点升高(溶质不挥发)和渗透现象是稀溶液的4个重要性质,并只与溶液中溶质的数量有关,而与溶质本身的性质无关,因此称之为稀溶液的依数性。范霍夫(van′t Hoff)首先发现了稀溶液的渗透现象,并提出了渗透压公式。因为这一成就,范霍夫获得了1901年Nobel化学奖。
尽管对稀溶液的渗透现象和渗透压的研究有着悠久的历史,我们还是发现目前国内部分物理化学教材对渗透压的定义及其推导过程存在不妥之处。鉴于渗透压在物理化学中的重要性,我们不揣冒昧在本文中将其指出来,希望引起读者的重视和思考, 也希望有关教材再版时加以纠正。
下面将首先介绍溶液中化学势的计算,接着是对渗透现象的分析和渗透压公式的推导及详细的讨论。
2 溶液中的化学势
对多组分溶液体系, 吉布斯自由能G不仅是温度和压力的函数,而且还是各组分物质的量的函数。吉布斯自由能G的全微分形式如下[1-7]:
(1)
式中S、T、V和p分别表示体系的熵、温度、体积和压力。nB和μB分别表示组分B的物质的量和化学势。从式(1)可以推导出化学势对温度和压力的偏导数有如下关系[1-3]:
(2)
式中SB,m和VB,m分别表示组分B的偏摩尔熵和偏摩尔体积。从式(2)得到化学势的微分式:
dμB=-SB,mdT+VB,mdp
(3)
从式(3)可看出, 在保持温度不变的情况下,如果组分B的偏摩尔体积大于0,则它的化学势将随着压力的增加而增加。这一点在推导渗透压时将用到。在多组分体系中,有了式(3),处理问题时就和单组分体系一样。
在多组分溶液体系中,等温下化学势的计算方式有两种:(a)利用气液平衡时气相中组分B的化学势和溶液中该组分的化学势相等,得到溶液中B组分的化学势;(b)利用式(3)直接积分计算。下面分别加以讨论。在某一溶液中,设气相为理想气体,B组分的分压为pB,则温度T时气相中B组分的化学势为:

(4)


(5)
式中μB(T,pB,aq)表示溶液中B组分的化学势;aq是水溶液英文单词的缩写,这里用以表示所有的溶液体系。假设溶液中B组分的蒸气压pB服从拉乌尔定律,即:
(6)
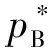

(7)
如果式(7)中xB等于1,则溶液变为纯组分B的液体,其化学势可表示为:
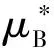
(8)
式中l表示纯组分B的液体,以与溶液(aq)区别。比较式(7)和式(8),μB(T,pB,aq)还可表示为:
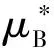
(9)
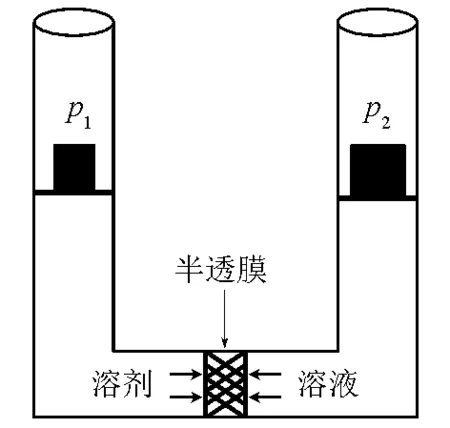
由于溶液中组分B的物质的量分数0 (10) 即: (11) 从式(11)可看出,如果组分B的偏摩尔体积VB,m大于0,则组分B的化学势随着压力的增加而增加,这与式(3)得出的结论是一致的。式(5)、式(7)、式(9)和式(11)都可以用来计算溶液中B组分的化学势。如果溶液中B组分的蒸气压pB服从亨利定律,其化学势的计算公式可采用上述方法得到。这里限于篇幅,不再赘述。 图1是稀溶液中溶剂往溶液中渗透的示意图。图中溶液和溶剂之间有半透膜,半透膜不允许溶质通过,只允许溶剂通过。但是,溶剂是从左边往右边渗透,还是从右边往左边渗透呢?这可以通过热力学知识来分析。将图1中左边的溶剂和右边的溶液看成一个体系,在等温等压情况下,式(1)可简化为: (12) 由于半透膜不允许溶质通过,式(12)中右边只需要考虑溶剂的贡献。这样,式(12)进一步简化为: (13) (14) 从上面的讨论可看出,为了阻止溶剂的渗透,必须增加溶液中溶剂的化学势。从前面对式(3)和式(11)的讨论中可以看出,如果溶液中溶剂的偏摩尔体积VA,m大于0,则溶液中溶剂的化学势将随着压力的增加而增加。在稀溶液中,溶剂的偏摩尔体积是大于0的,因此,对溶液加压将增加溶液中溶剂的化学势。如果溶液中溶剂的化学势等于纯溶剂的化学势,则纯溶剂停止向溶液渗透;如果溶液中溶剂的化学势大于纯溶剂的化学势,则溶液中的溶剂将向纯溶剂渗透。这种反渗透现象已用于海水淡化。 图1 纯溶剂向溶液渗透示意图 图2 稀溶液渗透平衡示意图 (15) (16) (17) 根据式(9),溶液中溶剂的化学势可表示如下: (18) 式中xA表示溶液中溶剂的物质的量分数。将式(18)代入式(17),整理后得: (19) 国内部分物理化学教材将渗透压定义为[4-7]: Π′=p2-p1 (20) 从式(19)可看出,要推导出渗透压的公式,不做近似是不可能的。要做的近似有如下两个: (21) (22) (23) 其中 Π=p2-pA (24) 在式(23)的推导过程中,假定溶液的压缩系数很小,VA,m近似为常数。式(23)就是物理化学教材中渗透压的计算公式。渗透压的定义式(式(24))有明确的物理意义。由于图2右边溶液中溶剂的化学势比纯溶剂的化学势低,因此,必须对溶液加压以增加它的化学势,当压力从其饱和蒸气压pA增至p2时,纯溶剂的化学势和溶液中溶剂的化学势相等,这时p2和pA之差称之为渗透压。用式(23)和式(24)计算得到的渗透压不仅是唯一的,而且是一致的。 国内部分物理化学教材推导渗透压公式通常采用下式[4,6-7]: (25) 式(25)的问题出在式右边的积分下限p1。p2是图2中右边溶液承受的压力,对溶液中溶剂的化学势有直接影响;但p1却是图2中左边纯溶剂承受的压力,既与溶液中溶剂的化学势无关,也与溶液中溶剂的偏摩尔体积VA,m没有任何直接的联系。因此,将p1作为对VA,m积分的下限是错误的。正确的积分下限应是pA。故式(25)应更改为: (26) 式(26)右边实际上就是在等温时对式(3)积分的结果。式(26)的物理图像很清楚,即为了增加溶液中溶剂的化学势以达到渗透平衡,溶液承受的压力从pA增到p2。对式(26)右边进行积分得到的结果与式(23)是一样的。这也从另一个角度说明渗透压的定义应该是式(24)而不是式(20)。 多组分体系中最重要的热力学概念就是化学势。有两种计算化学势的方式:一种是利用气液平衡时气液两相中同一组分的化学势相等这一关系来计算,由气相中某组分的化学势直接得到液相中该组分的化学势;另一种方式,就是对化学势的全微分形式积分来计算,利用吉布斯自由能可以解释溶液中的渗透现象,利用化学势可以推导出渗透压的计算公式。在推导过程中,我们发现目前国内部分物理化学教材对渗透压的定义不合理,没有唯一性,且与用式(23)计算出来的渗透压不一致。另外,这些教材有关渗透压的推导过程也存在不合理的地方。鉴于渗透现象和渗透压在物理化学教学中的重要性,我们在此将这些不当之处指出来,以引起广大教师和学生的重视和思考,也希望有关教材再版时加以纠正。 [1] 韩德刚,高执棣,高盘良.物理化学.第2版.北京:高等教育出版社,2009 [2] 天津大学物理化学教研室.物理化学.北京:高等教育出版社,2010 [3] 王淑兰,梁英教.物理化学.第3版.北京:冶金工业出版社,2008 [4] 傅献彩,沈文霞,姚天扬,等.物理化学.第5版.北京: 高等教育出版社,2009 [5] 印永嘉,奚正楷,张树永.物理化学简明教程.北京:高等教育出版社,2007 [6] 朱传征,褚蓉,徐海涵.物理化学.北京:科学出版社,2008 [7] 柴炳新.基础物理化学.第5版.北京:科学出版社,2006 CalculationofChemicalPotentialinDiluteSolutionandDerivationoftheOsmoticPressureEquation* Chen Feiwu* *Wei Meiju Ye Yaping Yuan Wenxia (SchoolofChemistryandBiologicalEngineering,UniversityofScienceandTechnologyBeijing,Beijing100083,China) There are two ways to calculate the chemical potential of a component in solution. One is that, in the gas-liquid phase equilibrium, the chemical potential of a component in solution is equal to its corresponding chemical potential in the gas phase; thus, the chemical potential of the component in solution can be easily obtained through the gas-liquid equilibrium once its chemical potential in gas phase is known. Another way is to integrate directly the total differential of the chemical potential of the component in solution. Based on this, a new way to derive the osmotic pressure equation is presented in this article. It is also pointed out that the definitions about the osmotic pressure in some domestic physical chemistry textbooks are not reasonable and the derivation of the osmotic pressure equation is not valid. Chemical potential; Osmotic pressure; Solution; Chemical potential 10.3866/pku.DXHX20150463 *北京科技大学研究型示范教学项目;北京科技大学教育教学改革项目(Nos.JG2011Z09,JG2013M41) **通信联系人,E-mail:chenfeiwu@ustb.edu.cn O6;G64
3 稀溶液的渗透压
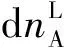
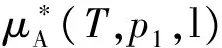



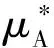
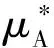

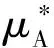
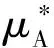
4 结论
