活动板类角反射器的RCS计算

吴春光，何四华，潘玉纯

（92941部队，葫芦岛 125000）

传统的角反射器由于其在较宽的角度范围内具有很强的后向RCS而被广泛用作RCS增强器和定标体。可是，在进行目标特性设计时，不仅希望作为靶标单元的角反射器具有很强的RCS，同时还希望能调节靶标单元后向RCS的主瓣宽度和主瓣方向，为此，本文研究带有活动板一类角反射器的RCS计算问题。

尽管二面角和三面角反射器的高频RCS计算不是一个新问题［1-7］，但是，对带有活动板一类角反射器的RCS计算却很少见公开报道。本文利用几何光学（GO）和物理光学（PO）的方法，即中间反射过程采用GO法，最后一次散射采用PO法计算带有活动板一类角反射器的高频散射，虽然与Knott［2］和Anderson［4］在求解非正交二面角反射器的后向RCS时采用的方法类似，但是本文工作更侧重于针对多次反射的一般性考虑，以使本文计算方法具有通用性。

1 计算方法

利用GO+PO方法计算带有活动板类角反射器的RCS，关键问题是如何处理任意面元对之间的多次反射和遮挡判断问题。基于一般性，考虑图1所示由多块平板构成的腔体目标的多次反射问题。多次反射中电磁波可以照射到的面称为照射面，位于入射照明区的照射面称为可见面，位于入射阴影区的照射面称为不可见面。一束平面波照射该目标，两条虚线中间的区域表示腔体内部的入射照明区，照明区内一条射线入射到腔体发生多次反射，其中二次反射和三次反射的照射面位于入射阴影区，对目标后向散射无贡献。可以看出，在入射波的四次反射中，仅第一次反射和第四次反射的照射区域对目标的后向散射有贡献，并且贡献最强的是第四次反射照射区域的散射贡献。因此，在多次反射分析中，不仅要考虑可见面的反射，还应该考虑不可见面的反射。

图1 平板腔体目标多次反射示意图

从图中还可以看出，二次反射的照射面位于入射阴影区，其二次反射对目标后向散射无贡献。当仅考虑到二次反射时，也就是忽略三次以及三次以上多次反射贡献时，对不可见面元进行二次反射面元对的判断是无意义的。考虑三次以及三次以上多次反射时，由于不可见面的多次反射不能忽略，应该在整个区域对所有面片进行多次反射面元对的判断。通过上面的讨论，可以得到以下结论：

（1）反射到可见面上的多次反射对目标后向散射产生贡献；

（2）与目标不相交的反射线将不会再产生多次反射；

（3）在复杂目标的多次反射中，每次反射都需要进行多次反射的遮挡处理、多次反射面元对的判断以及多次反射照射面的确定；

（4）多次反射照射面需要进行可见和不可见的判断，对于部分可见的多次反射照射面应当进行裁剪以获得照射面中的可见部分。

1.1 多次反射的计算流程

对于给定的目标，首先根据入射波方向对目标进行遮挡处理，处理后得到的面片分类成一次入射的可见面和不可见面。每一个面与一次入射可见面之间发生的多次反射对后向散射有贡献，与一次入射不可见面之间发生的多次反射对后向散射无贡献。因此，这样就不必进行多次反射照射面的可见和不可见的判断，同时也不存在部分可见面的情况。采用可见面和不可见面表示原始模型，虽然表示模型的平面数会有所增加，但问题的处理大大简化。

在计算第M次反射贡献时需要根据第M-1次反射中的照射面和几何光学反射场方向确定发生第M次反射的照射面，并将照射面分为第M次反射可见面和不可见面。对所有第M次反射可见面进行物理光学积分可以得到第M次反射的后向散射贡献。在计算第M次反射时，第M次反射照射面的判断是比较复杂的过程，其步骤如下：

（1）选择第M-1次反射照射面中一个照射面O，根据平面O的多边形形状、位置以及第M-1次几何光学反射方向确定与一次可见面可以发生第M次反射的所有面Pi(i=1,2,…,p)；

（3）确定面O反射场在面Qi(i=1,2,…,q)中的照射区域，得到第M次反射的照射面Ri(i=1,2,…,r)；

（4）对所有的M-1次反射照射面重复以上操作得到所有M次反射照射面中的可见面；

（5）对所有M-1次反射照射面和一次不可见面进行类似于上面的判断，可以得到所有M次反射照射面中的不可见面。

当不存在多次反射照射面或多次反射的次数已达到预先设定的最大多次反射次数时停止运算。整个计算过程中需要反复进行的就是多次反射遮挡处理和多次反射照射面的确定。多次反射的遮挡处理同一次入射的遮挡处理方法类似，不同的仅仅是入射波方向的选取。遮挡处理包括多边形的相交判断和多边形平面的裁剪运算两部分［8］。

1.2 多次反射场的物理光学计算

对尺寸与入射波波长相比较大的目标，可以利用PO近似计算目标的远区散射场。略去时谐因子为ejωt，物理光学目标远区散射场为：

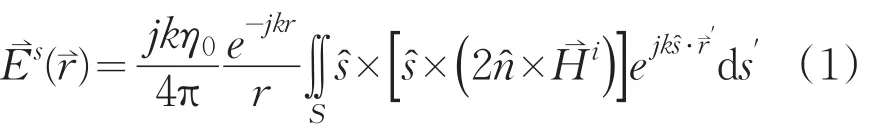
若设入射电场具有幅度E0和极化矢量，选择入射波在坐标原点处相位为零相位，则入射场可以表示为：

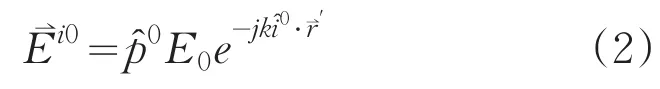
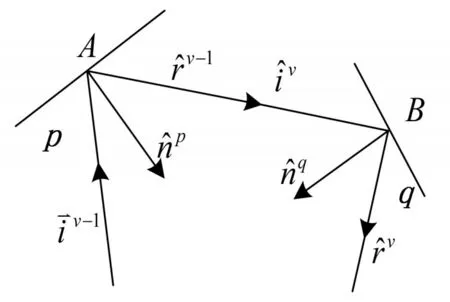
图2 多次反射示意图

如图2所示，p板和q板之间发生多次反射，入射波在p板发生第v-1次反射，p板上的反射场在q板上发生第 p次反射。可以看出，第 p次反射的入射场恰好是第 p-1 次反射场，即 E⇀iv=E⇀r(v-1)，iv=rv-1(v=1,2,…,N)，其中 N 表示给定最大的多次反射次数。对一次反射，E⇀i1=E⇀i0，i1=i0。则第v次几何光学反射场可以表示为：

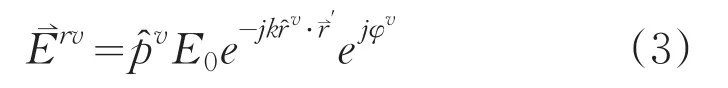
式中，rv表示第 p次反射方向的单位矢量，Pv表示反射场极化方向单位矢量，φv表示参考相位。

当第v次反射的平面位于照明区时，将产生第v次反射的入射场代入（1）可得第v次反射照射区域的远区散射场。对给定的散射方向，s是常量，而入射场随着多次反射的发生不断变化。单站情况下，则第 v 次反射照射区域的远区后向散射场为：

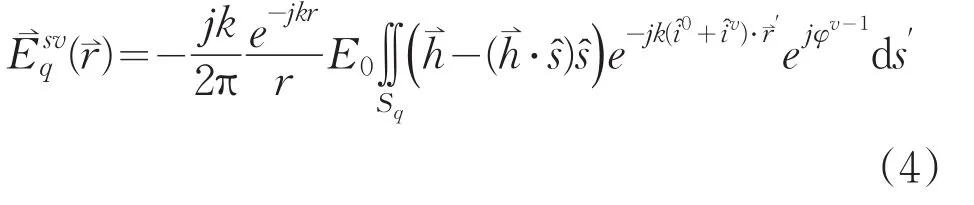
最后，目标的RCS为：

式中，N表示所计算的多次散射的次数，num（v）表示第v次散射中的可见面的数目，Pr表示雷达接收极化方向，对于同极化接收，Pr=P0。由于所有面元都采用凸多边形平面单元，因此公式（4）的计算可以采用Gordon［9］的方法将面元积分简化为顶点求和的运算。

2 计算实例

以常规正方形三面角反射器和两种带活动板的三面角反射器为例，利用上述方法进行数值计算，如图3所示，（a）为常规正方形三面角反射器，三个反射面由三个边长为lm的正方形导体板相互垂直拼接而成；（b）为侧翻板型三面角反射器，在常规三面角反射器两侧增加两个边长为lm的正方形侧翻板，两板都与底板垂直，两个侧翻板与垂直板之间夹角为δ，并且夹角可调整；（c）为在常规三面角反射器上方增加一个边长为lm的正方形板，其中上翻板和角反射器一个角点在上顶点固定，翻板仰角为β，且仰角可调节。

三类角反射器边长均为lm=50cm；对侧翻板型角反射器，侧板夹角δ=135°；对上翻板型角反射器，翻板仰角 β=35.26°；入射波频率 f=15GHz，极化为VV。

为了验证本文计算方法的正确性，图4给出了俯仰角θ=62°时，图3（b）所示侧翻板型三面角反射器在方位角内的后向RCS计算值和测量值。可以看出计算值和测量值吻合的非常好，从而验证了本文方法在计算多次反射中的有效性和正确性。

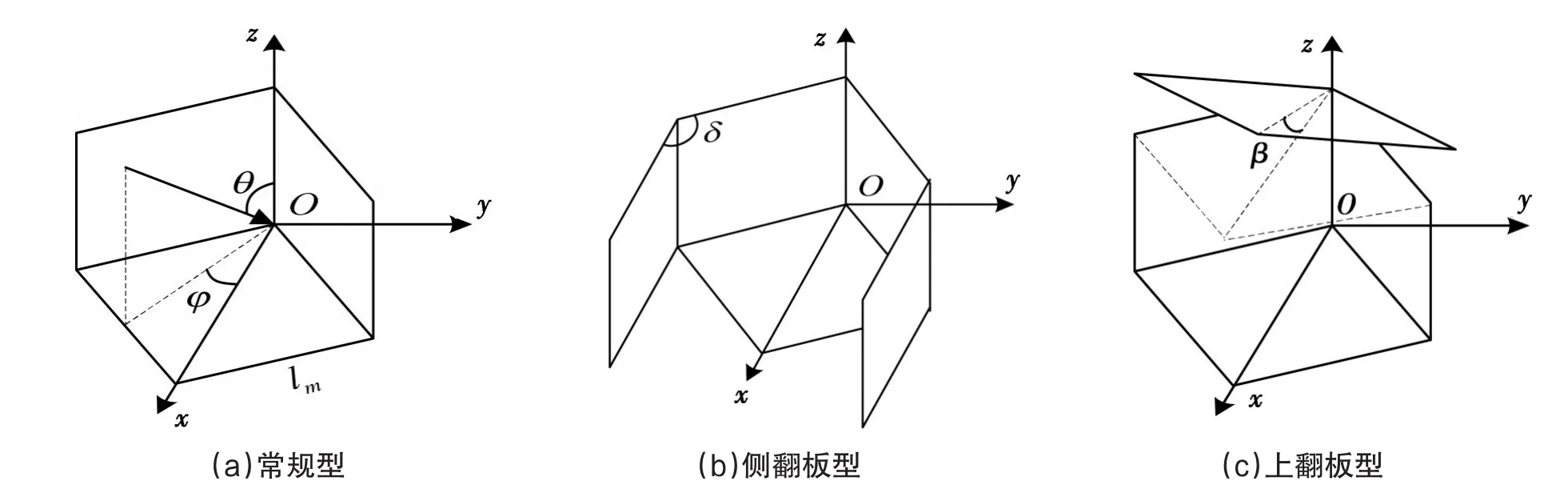
图3 三面角反射器的几何结构

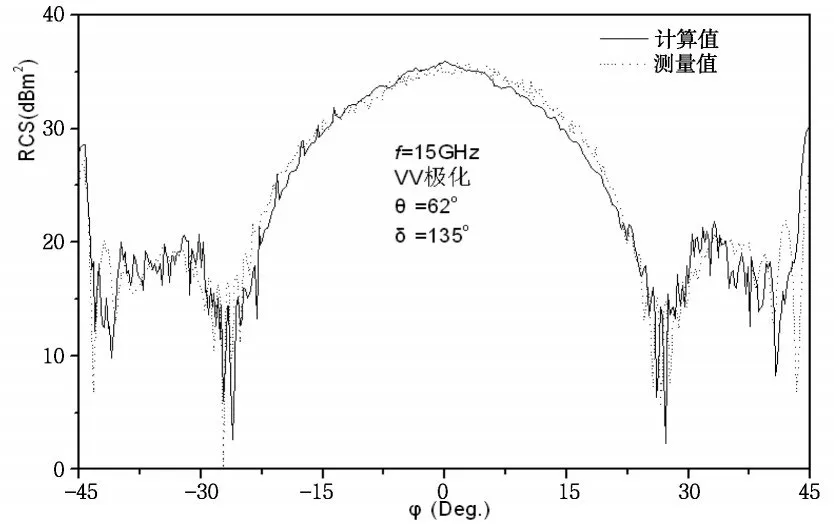
图4 带侧板型角反射器后向RCS

为了验证带有活动板三面角反射器对三面角反射器后向散射波束角度范围的调节作用，需要分别比较常规型角反射器同侧翻板型角反射器以及常规型角反射器同上翻板型角反射器的后向RCS。图5给出了图3（a）所示常规型角反射器和图3（b）所示侧翻板型角反射器在俯仰角θ=54.74°时的后向RCS。通过比较可知，常规型角反射器加上侧翻板后，对相同的俯仰角沿方位向的后向散射主瓣宽度变窄。因此，通过适当调整侧翻板夹角可以调整沿方位角方向的后向散射主瓣宽度。

图5 常规三面角反射器的后向RCS

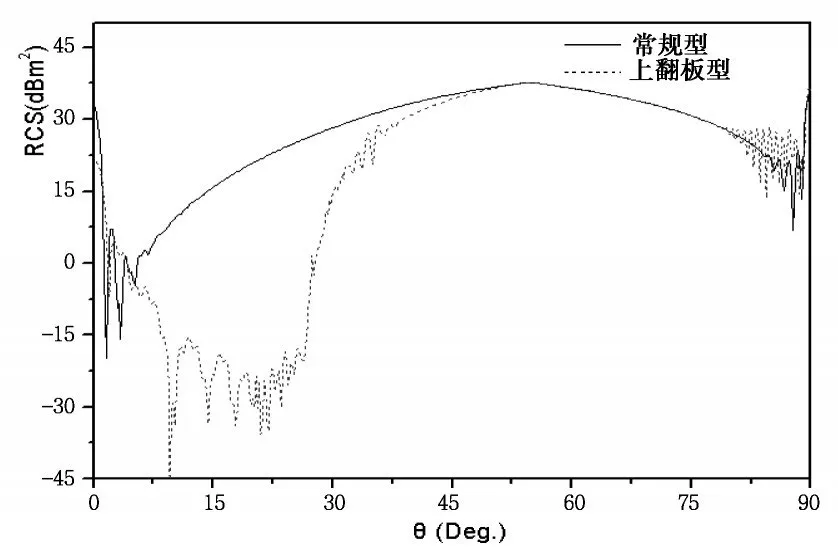
图6 带侧翻板型三面角反射器的后向RCS

图6给出了方位角φ=0°时图3（a）所示常规三面角和图3（c）所示上翻板型三面角反射器后向RCS。比较两条曲线可以看出，通过增加上翻板，在相同的方位角上沿俯仰方向的后向散射主瓣宽度在低俯仰区域压缩变窄，高俯仰区域散射基本不发生变化。因此，通过调整上翻板的俯仰角可以调整沿俯仰方向低俯仰角区域的后向散射主瓣宽度。

3 结论

本文利用几何光学（PO）+物理光学（PO）的方法计算带有活动板的角反射器的高频散射，给出了用于计算由任意平板构成的复杂目标多次反射的通用方法，可以准确地完成平板目标内可能存在的多达上百次的多次反射计算。对带侧翻板型和带上翻板型的两种三面角反射器的RCS计算结果获得与测量结果较好的一致性。

研究表明，带侧翻板和上翻板的角反射器对常规三面角反射器后向散射主瓣宽度具有较好的调节作用，即侧翻板调节沿方位角的后向散射主瓣宽度，上翻板调节沿俯仰角的后向散射主瓣宽度。利用本文的计算方法，可以完成反射器的优化设计，对给定的极化和频率，在预定的一些空间姿态角上获得所希望的RCS方向图。

［1］Andrsde L A，Nohara E L.Backscattering analysis of flat plate and dihedral corner reflectors using PO and comparison with RCS measurements in anechoic chamber［J］.IEEE MTT-S IMOC，2003：719-724.

［2］Knott E F.RCS reduction of dihedral corners［J］.IEEE Trans.Antennas and Propagat，1977，25（3）：406-409.

［3］Xia Dongyu，Qin Kaibing，Pan Yingfeng.An improved hybrid technique for computing the RCS of dihedral corner reflector with a protrusion［J］.IEEE Microwave，Antenna，Propagation and EMC Technologies for Wireless Communications，2009：900-902.

［4］Anderson W C.Consequences of nonorthogonality on the scattering properties ofdihedralreflectors［J］.IEEE Trans.Antennas and Propagat，1987，35（10）：1154-1159.

［5］Balanis C A，Polka L A，Polycarpou A C.High-frequency Techniques for RCS prediction of plate geometries and a physicaloptics/equivalentcurrents model for the rcs of trihedral corner reflectors［R］.NASA-CR-195140 NO：TRC-EM-CAB-9402，1994.

［6］Ferrara G，Mattia F，Posa F.Backscattering study on non-orthogonaltrihedralcorner reflectors［J］.IEEE Porp.-Microw.，Antennas Propagat.，1995，142（6）：441-446.

［7］Li Chengfan，Zhao Junjuan.Analysis of RCS characteristic of dihedral corner and triangular trihedral corner reflectors［J］.IEEE Computer Science and Education（ICCSE），2010：40-43.

［8］孙家广.计算机图形学［M］.北京：清华大学出版社，1998.

［9］Gordon W B.Far-Field Approximation to the Kirchoff-helmholtz Representation ofscattered Field［J］.IEEE Transaction on Antennas and Propagate，1975，23（7）：590-592.