多波段激光合束镜温度适应性分析

孙毅，高云国，邵帅

（1.中国科学院长春光学精密机械与物理研究所，长春 130033；2.中国科学院大学，北京 100039）

随着激光应用的发展，将不同波段激光进行非相干合束，获得多波段、大功率输出效果对于高能激光应用、远距离激光传输等方面有着重大的意义。

ZnSe是综合性能较好的合束镜材料。对0.67～14μm波长光束有着超过60%的本征透过率，有良好的机械物理性能［1］。本文利用透长波激光反短波激光的合光模式将10.6μm红外激光以及0.808μm可见光激光进行非相干合成。

在激光合束过程中，合束镜由于表面膜层以及基体材料的吸收，部分光能转化为热能，使得面形、基体材料折射率产生畸变，对激光质量产生影响。ZnSe相较其他材料热导系数较小，短时间内温度在局部区域积累更为明显。研究其热畸变对输出激光质量的影响很有必要。在实际应用过程中，在近场很难测量合束镜对通过的高功率激光光束质量，远场测量所需设备庞大，干扰因素较多，对数据采集也有一定困难。所以利用有限元手段，在设计之初对合束镜的温度场、位移场、远场光强等进行模拟仿真很有必要［2］，对红外激光合束镜的温度适应性分析提供了数据支撑和分析方法。

本文结合工程上实际应用，对高能激光系统红外材料ZnSe平面镜建立有限元模型，分析了环境温度对合束镜出光质量的影响，并结合远场理论建立了从材料选择到实际应用的一整套分析方法。用远场光束质量作为评价激光透射镜受环境条件影响的指标，使得环境因素更加透明具体。该套方法也同样可以应用到激光窗口、平面反射镜等激光应用中。

1 合束镜瞬态温度场分析

合束激光中激光长波激光通光口径为100mm，短波激光口径为40mm，入射角度为45°，由于长波激光在镜面上光斑呈现椭圆形（椭圆长轴141mm，短轴100mm），所以镜体尺寸设计为200mm×140mm×20mm。激光合束示意图如图1所示。为方便后文叙述，将长波激光入射面设为表面1，短波激光反射面设为表面2。

图1 激光合束示意图

激光辐照镜体表面时，膜层以及基体吸收部分激光能量，将光能量转换为热能量，镜体温度分布不均匀使得内部及表面产生热传导过程，工程上常利用有限元方法分析这种边界条件复杂的三维瞬态热传导问题。在激光辐照过程中，瞬态热平衡方程为：

式中[KT]为传导矩阵，包含导热系数和对流系数；为比热矩阵；{T }为节点温度向量；为温度对时间导数；{}Q 为热源产生温度载荷。将热流作为热载荷，给予分析模型外部初始温度条件以及热对流条件。通过有限元分析软件即可求得瞬态温度场。合束镜经过镀膜后可以大幅提高透射率以及反射率。因透射镜基底热扩散径向长度远大于膜层总厚度，所以只考虑基底材料内热传导方程，将膜层热吸收作为边界条件。根据膜层吸热率计算，净吸收功率为50W。

对热分析做如下说明（1）吸收的功率作为热流密度均匀分布于光照区；（2）由于大尺寸合束镜没有温度调节措施，对流换热系数根据经验选择为14W·m-2·℃［3］；（3）镜子初始温度设为与环境温度一致；（4）由于激光作用时间较短，镜体通过基座热传导对温度场变化作用较小，忽略基座与镜体热交换；材料属性如表1所示。计算激光辐照90s后的瞬态温度场。在这里本文以与实验室环境（20℃）温差最大的-40℃作为典型分析。

表1 材料的主要参数

图2所示为-40℃时ZnSe材料的温度场分布。由图可以看出，在90s辐照后热量在辐照区域集中，温度上升11℃，镜体内部出现不均匀温度场分布，产生径向温差与轴向温差。取镜面X方向对称轴，并取两对称轴中心点绘制径向以及轴向温差随时间变化曲线如图3所示。径向温差主要影响面型的变化，轴向温差对折射率的变化产生影响。可以清楚的看出ZnSe材料径向温差随时间逐渐增大，最大达到8.5℃，并没有明显的收敛趋势。这说明吸收的热能量大于对流散热所失去的能量。轴向温差在20s时逐渐达到稳定状态。其轴向温差始终保持在2.2℃范围内。

图2 ZnSe-40℃温度场分布

图3 随时间变化的温差（-40℃）

温度场的分布同时也带来了折射率的改变，在轴向方向形成“热透镜”效应，折射率的计算公式为：

其中，n0为材料在20℃时的相对折射率，α为材料的热光系数。在温度t=20℃，λ=10.6μm时，折射率为2.4028，α =6.1×10-5。

提取有限元节点温度数据并带入到编制的Matlab程序中，将温度转换为折射率的函数。计算出各节点折射率并将折射率变化产生的光程差影响带入到后续计算中。

2 合束镜的热变形分析

合束镜采用三点压块式夹持，其结构如图4所示。

图4 合束镜结构图

通过研磨调整凸台等手段，在实验室利用干涉仪装调可以显著降低装调应力所带来的面形畸变。因此在有限元分析中，剥离刚体平移造成的变形，只考虑Z轴方向的变形。非均匀的温度场导致非均匀的热膨胀。热应力-应变之间关系为：

式中，D为弹性矩阵，ε0=α(T-T0)[111000]T为初应变，根据弹性力学虚位移原理，进行数学处理即可得到节点位移矩阵方程：

式中，KC为结构刚度矩阵，PC为结构载荷矩阵，是体积载荷PV、表面载荷PF、温度载荷PZ之和。对上式进行求解，即可得到镜体的位移场以及应力场结果。将计算出来的温度场作为空间场加载到有限元模型上，约束条件为两个压块分布在镜体上部斜边，另一个压块约束镜体底边平行于X轴，压块上表面与底部凸台限制UZ方向自由度，压块接触镜体部分约束UX、UY方向自由度。约束位置以及有限元模型如图5所示。计算在各个温度环境下的Z轴方向变形。

图5 约束条件以及静力分析有限元模型

图6是在环境温度和激光热效应耦合作用下的90s时刻合束镜变形云图。

图6 不同温度条件下的变形云图

可以看到在环境温度和激光辐照热效应的耦合热冲击下，合束镜的变形量分布极不规则，镜面畸变使得镜面变为球面。对于这种红外合束镜来说，面型畸变只是造成光束质量下降的一部分因素，不能简单的以变形量或变形方向去衡量［4］。离散的有限元数据需要通过数学计算拟合形成完整的波面数据。Zernike多项式结构和光学之间良好的接口，利用Zernike多项式拟合其变形后的面型数据和折射率畸变同时利用衍射理论计算远场光束质量。

3 光束质量分析

3.1 Zernike拟合合束镜波前畸变

Zernike多项式是光学和结构之间良好的接口软件。直角坐标系下的N项Zernike多项式为：

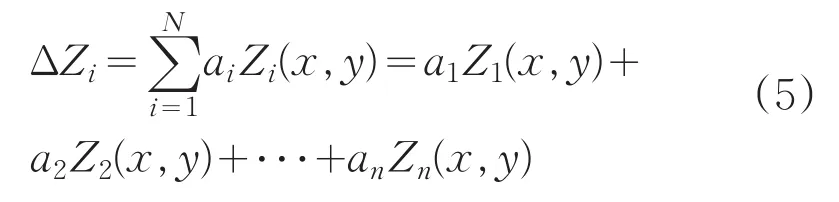
式中，ai为Zernike第i项系数；zi(x,y)为Zernike多项式第i项；x,y为有限元输出的节点坐标［5］。将多项式表示为矩阵形式后，通过Householder对矩阵进行正交三角化后利用最小二乘法即可解出各项系数，即可求得拟合后的面型。

图7为一束平面波光束沿Z轴传播，Z1和Z2为入射光一侧以及出射光一侧参考面。

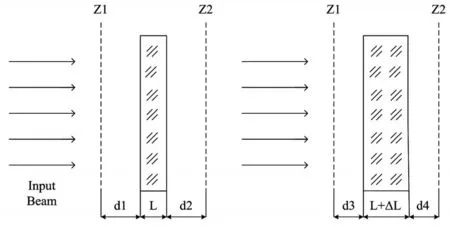
图7 热效应模型

忽略应力双折射产生的光程差［6］，则可以得到总光程差为：

当光束以θ角度入射时，其光程差［7］公式为：

式中，ΔDΔL为镜面畸变产生的光程差，ΔDΔt为折射率变化带来的光程差，ΔL为Z轴方向厚度的变化量。

具体计算方式为：（1）利用Zernike多项式拟合上表面U1(x1,y1)和下表面面U2(x2,y2)；（2）有限元网格将Z轴划分为15层，计算每层节点折射率变化所带来的光程差改变［8］，将累计的光程差保存为矩阵KOPD。累加后的光程差作为Z轴，以下表面横纵坐标为x，y再次利用最小二乘法将光程差拟合为U3(x3,y3)；将两部分叠加形成UOPD(x,y)。

3.2 光束质量分析

将拟合后的波前畸变带入到计算激光传播的夫琅禾费公式，即可求得光束远场光强的分布。其公式［9］为：

式中，λ为波长，z=UOPD(x,y)温度导致的波前畸变，为波数，编制相应的Matlab程序，将有限元数据导入计算远场光强分布［10］。

对于强激光发射系统，衍射极限倍数β和环围功率比BQ是比较理想的光束质量参数。为了量化热畸变对远场光束影响，使用环围能量86.5%能量光斑半径之比计算光束质量β系数以及BQ［11］。如图8（a）所示，在-40℃条件下，光束经过畸变的合束镜后，光强最大值依然在光斑中心，但是在光斑周围出现较为明显的衍射环，峰值光强相对理想传播下降近20%。波前畸变WPV=0.59λ（λ=10.6μm）；β =1.761，BQ=1.175。图8（b）所示为在50℃条件下的远场分布，光斑形状保持较好，峰值光强相对理想状态下降10%，衍射环虽然已经出现，但与理想传播相比，光斑撕裂现象不是很明显，环境温度对整体光束质量影响较小，WPV=0.56 λ，β =1.465，BQ=1.050；虽然相对于20℃的温度条件（WPV=0.27λ，β=1.062，BQ=1.025），β系数下降38%和65%，但依然满足设计要求β＜2.5。光强峰值和桶中功率保持较好，在-40℃～+50℃温度范围内计算的β系数以及BQ如表2所示。

图8 10.6μm远场光强分布

短波激光以反射方式参与合束，对光束质量影响的主要因素是表面2的面型畸变。根据夫琅禾费理论，衍射现象扩散程度与孔径成反比，这就意味着短波长激光对热畸变更加敏感。表2中显示了在不同温度条件下短波激光在不同温度条件下的的β系数以及BQ，可以看出环境温度热冲击对0.808μm产生的影响可以忽略不计。这是因为短波激光口径小，辐照局部区域畸变相对整个镜面区域畸变较小，在局部镜面型可类似于平面镜状态，所以光束传播未受影响，接近衍射极限。

表2 不同温度下的β、BQ参数

4 结论

本文对多波段红外ZnSe材料透镜进行了温度适应性的光-机-热耦合分析。针对实际使用温度条件，以-40℃作为典型分析，将环境温度对光束质量的影响作出定量分析。研究结果表明：针对波长为10.6μm激光，在-40℃～+50℃环境温度范围内。激光光束质量保持较好，β最大值为1.761，BQ最大值为1.175；针对短波激光，由于其口径较小，使得辐照区域热畸变分布均匀，光束接近衍射极限，β最大值为1.072。在使用温度范围内，两种波长激光均满足合束镜温度设计要求。相关分析过程可以运用到大功率红外材料透镜以及激光窗口等问题中。

［1］么艳平，刘景和.ZnSe红外窗口材料的性能及其制备［J］.人工晶体学报，2006，35（1）：183-184.

［2］贾勇，高云国，邵帅.热载荷下扩束系统的光机优化设计［J］.中国激光，2014，41（1）：0116003-2-0116003-6.

［3］冯树龙.地基望远镜力学、温度场特性对光学性能影响研究［D］.长春：中国科学院长春光学精密机械与物理研究所，2005：76-84.

［4］石进峰，吴清文，张建萍，等.高空高速航空相机光学窗口 的 热 光 学 分 析［J］.光 学 学 报 ，2012，32（4）：042004-02-042004-08.

［5］杨佳文，黄巧林，韩友民.Zernike多项式在拟合光学表面面型中的应用与仿真［J］.航天返回与遥感，2010，31（5）：49-55.

［6］孙峰，程祖海，张耀宁，等.在波长1.315μm下几种激光器窗口热效应比较研究［J］.中国激光，2004，31（4）：412-416.

［7］裴正平，唐淳，涂波，等.Nd：YAG薄片激光器热致波前畸变［J］.强激光与粒子束，2006，18（10）：1615-1618.

［8］赵立新.空间太阳望远镜的热设计和热光学分析［J］.航天返回与遥感，2010，31（5）：49-55.

［9］吕乃光.傅里叶光学［M］.北京：机械工业出版社，2007：93-94.

［10］Jason D Schmidt.Numerical Simulation of Optical Wave Propagation［M］.Washington：SPIE Press，2012：55-58，65-75.

［11］高卫，王云萍，李斌.强激光光束质量评价和测量方法研究［J］.红外与激光工程，2003，32（1）：62-64.