周视红外搜索系统对空中目标的搜索模型

贾庆莲

（中国科学院长春光学精密机械与物理研究所，长春 130033）

周视红外搜索系统又称周视预警系统，用以在方位360°范围内，对目标进行搜索、探测并提供预警信号［1-3］。该系统可以应用在陆地、飞机、舰艇等多种场合，是现代化多层次、多方位战争中不可缺少的重要军用光电系统之一［4，5］。

搜索［6-8］是指面对的大多是未知目标，且有时间严格限定的任务。目标的运动特性一般情况下是未知的，因此，目标运动和目标位置的所有参数，或某些参数相对搜索来说都可以看成是随机的、相互独立的参数。

目标与搜索设备的相对位置和相对速度都可以用已知的运动特性的概率密度来说明。而组织搜索的搜索设备的运动规律是已知的，这种情况下，最常遇到的问题是目标可能位置的分布问题，是均匀分布还是正态分布。

从工作方式上看，周视搜索系统的方位搜索多采用扫描头360°旋转扫描，旋转速度为0.2～3r/s，俯仰搜索采用螺旋式或步进式来覆盖。

本文建立了一个周视扫描模型［9］，分析了固定载体周视扫描模型及动载体周视扫描模型，并在此基础上分析了针对空中目标的搜索模型。

1 周视扫描模型

1.1 固定载体周视扫描

假设目标在方位0～2π范围内是均匀分布的，其活动面积S为已知，且目标在其中的位置为均匀分布，而目标的运动方向在(0～2π)范围内均匀分布，但位置未知。

图1 搜索者为匀速圆周运动目标为直线运动模型图

目标相对搜索者的运动如图1所示。搜索者做绕M点的匀速圆周运动，搜索设备第一次发现目标时，即目标出现在系统瞬时视场α×β（方位角α，俯仰角β）内，在一次搜索扫描周期内目标相对搜索设备转动的最大角度为qt，qt应满足以下关系。

图2 目标在一次扫描周期内的运动

设目标速度Vg，搜索设备方位扫描周期为ts，搜索者与目标间距离rt，目标指示误差为δα，如图2所示，则

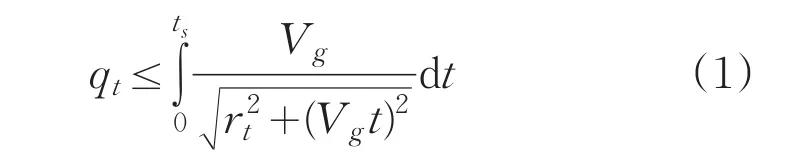
在三角形ΔMG0Gt

在不了解目标航速的情况下，一般认为目标有一个最大航速Vmax，这种情况下认为目标航速大小的分布密度为等概率规律，其分布密度为

设搜索设备的起始点为M0，视轴指向为M0KM，目标刚进入设备作用距离的初始点在T0，目标跑出作用距离的终止点为T4，航向T0T4，搜索设备距目标初始距离为r0。设在整个过程中，目标与设备相遇4次，在ΔM0T4T0中作∠M0T4T0的四等分线交直线T4T0分别于T1、T2、T3、T4点，则有目标与搜索者的相遇关系如图3所示。

图3 目标与匀速圆周运动搜索者的相遇关系图

在图3所示关系中，

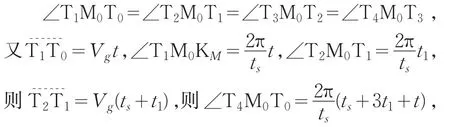
1.2 动载体周视扫描

设在大地坐标系中，搜索者的运动方程为

式中αM为搜索航向方位角，βM搜索航向俯仰角，如图4所示。目标相对搜索者的运动方程为，如图5所示。

图4 目标与搜索者都为匀速直线运动图

图5 目标与搜索者运动速度图

由余弦定理得

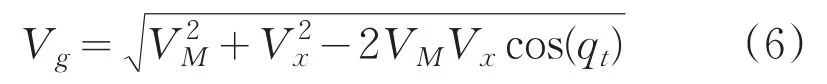
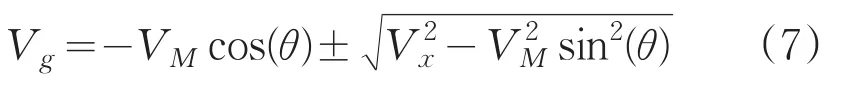
设搜索设备的起始点为M0，视轴指向为M0KM，目标初始点在T0，航向T0G3，搜索设备距目标初始距离为r0。在ΔM0G3T0中作∠M0G3T0的二等分线交直线M0T0于G1点，作∠KMG3T0的二等分线交直线M0T0于G2，则有目标与搜索者的相遇关系如图6所示。

由图5所示关系得，

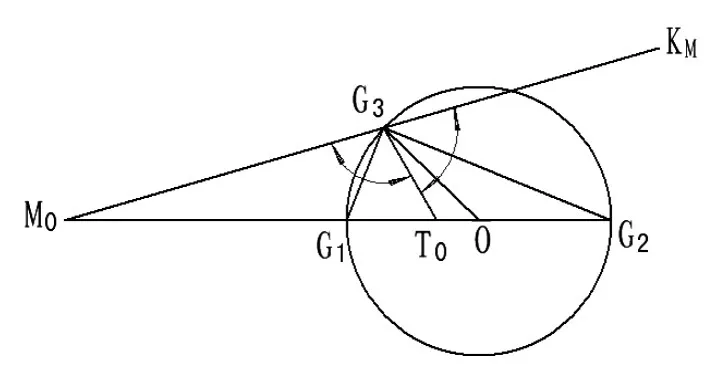
图6 目标与直线运动搜索者的相遇关系图

2 仿真分析

2.1 时间配准

当完成搜索任务的各个系统中探测器分布范围很大，取得的目标位置数据往往是异步状态的，它既包括时间的不同步，也包括目标在空间上的偏差。如果要取得较好的定位精度，必须在定位之间将各个探测器的方位数据进行同步，如何实现数据的同步，如何在无法消除测量误差的情况下，利用同步的方位数据，来对观测目标进行有效的定位，将是一个需要研究的问题。

在相同设备相同采用频率的前提下，时间不同步方面的主要原因有：由于线阵探测器在周视扫描过程中，一次扫描可能只能获得一次或几次采样，同步扫描的线阵探测器无法在空间有一个重叠范围；在采样过程中，来自不同设备的观测数据通常不是在同一时刻得到的，存在着观测数据的时间差。对于相同的几台传感器，由于观测到目标的时间不同，或者在观测时间内某台传感器丢失目标，要通过交会处理完成获取目标信息，必须选取一台传感器的时间为基准，然后将其它传感器上的时间向其配准。

几台同步扫描的采样周期相同的设备由于在同一个扫描周期内时间相差Δti-j，0≤Δti-j≤T0，当采用时间对齐技术，每个时刻以采样周期T进行预测时，所需要的预测步数Δti-j/T较多，因此要求预测算法的实时性要好。

采用自适应α-β滤波来预测下一时刻的目标数据，再结合同一目标已有的估计值，采用插值法获得较高的精度，理论上可以既保证实时性又保证精度。

将M站时间外推以配准到K站的测量时刻的具体过程如下：

（1）对第 M(M=1,2,…,N,M≠K)传感器，设初时，传感器测量的α 和m,jmTi作为，由此确定

（2）在搜索站传感器M的数据处理中，把当前观测值和上一时刻对当前时刻的预测值代入方程，计算残差，并结合前N-1个残差，计算方差σ2k(k)；然后计算目标机动指数r；并计算自适应系数αz(k)，βz(k)；

（4）计算t1时刻的量测值：Zm,1；（5）按公式计算，转计算步骤（2），直至计算得

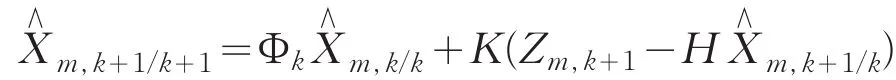
（6）交会中心从带搜索站K的数据中提取同一目标的需要配准的时间点t，t=tK,i,j，从M估计值数据中提取最近两点的时间tk-1、tk和预测点的时间tk+1；

依此将K站以外的几余各站的时间全部配准到第K站，然后进行空间交会处理计算。

2.2 仿真试验

通过给定目标的运动航迹，采用红外探测器作为周视搜索设备，分析了本文模型算法的航迹拟合结果。设搜索系统的测角误差为σα=0.4mard,σβ=0.4mard 。

设目标运动航迹（1）为方向向量为（1 1-0.2）的空间直线，起始位置为（2000-2000 5000），起始速度为0m/s，中间加速度为56m/s2，目标在40s内作匀加速运动，40s以后匀速运动。则三维空间中的目标角度航迹如图7所示，其方位角、俯仰角误差值如图8所示。

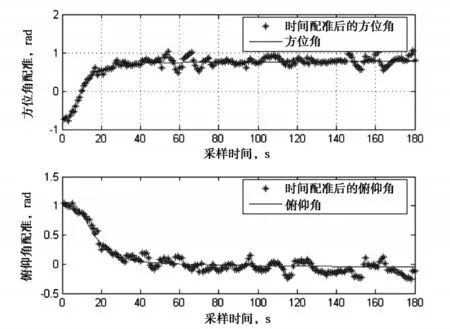
图7 航迹一的目标方位角、俯仰角及配准后数值

从图7和图8可以看出，经过航迹拟合起始及时间配准后的方位角、俯仰误差在扫描初始（采样开始阶段）较大，当采样时间大于4s，也即搜索系统扫描接近4圈以后，方位角误差及俯仰角误差都趋向平稳，针对本文给定的测角误差，方位角误差幅值在0.06～0.09mrad，俯仰角误差幅值在0.05～0.1mrad之间振荡。

设目标运动航迹（2）为方向向量为（1 1 10）的空间直线，起始位置为（2000-2000 100），起始速度为0m/s，中间加速度为100m/s2，目标在10s内作匀加速运动，10s以后匀速运动。则三维空间中的目标角度航迹如图9所示，其方位角、俯仰角误差值如图10所示。

图8 目标方位角、俯仰角配准误差

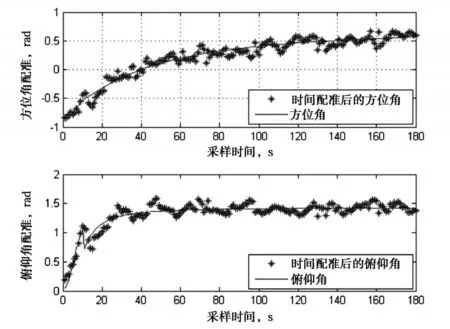
图9 航迹二的目标方位角、俯仰角及配准后数值

图10 目标方位角、俯仰角配准误差

从图7至图10可以看出，对于不同的目标航迹，航迹拟合起始后再时间配准的算法精度较高，针对实验条件中提到的测量误差，方位角误差大约为0.07mrad左右，俯仰角误差大约为0.08mrad左右。

3 结论

周视红外搜索系统由于其接收目标自身发射或反射其它光源的辐射信息，隐蔽性好等特点，在光电对抗、光学遥感及光电防御等领域得到了重视。因此利用被动光学原理的红外搜索系统就变得极其重要，研究搜索模型就成为必要。

本文针对固定载体和动载体研究了周视搜索的模型，并且对空中目标的搜索方法进行研究，详细分析了面积搜索及线上搜索的模型及原理。在多台红外搜索系统同时对空进行搜索监视的工作状态下，利用时间配准原理，仿真试验分析了时间配准后针对本文建立的搜索模型，空中目标的搜索测量误差，其方位角误差大约为0.07mrad左右，俯仰角误差大约为0.08mrad左右。

［1］裘展国（译）.目标搜索［M］.七零五研究所，1983：1-10.

［2］高稚允，高岳，张开华.军用光电系统［M］.北京：北京理工大学出版社，1996：192-196.

［3］宋丰华.现代空间光电系统及应用［M］.北京：国防工业出版社，2004：205-211.

［4］舒金龙，陈良瑜，朱振福,等.国外红外搜索跟踪系统的研究现状与发展趋势［J］.现代防御技术，2003，31（4）：47-51.

［5］侯志恒，曹玉东.红外警戒系统的多目标跟踪［J］.电光系统，2005（3）：21-22.

［6］Homan S Roger，Robert M Headley.Seaborne electro-optical sensors and their technologies［A］.Proceedings of SPIE，3698［C］.1999：12-20.

［7］Meimei Z.New infrared sensors for ballistic missile defense［A］.SPIE，Quantum sensing and nanophotonic devices II［C］.2005，5732：217-224.

［8］小哈德逊R D.红外系统原理［M］.北京：国防工业出版社，1975：201-205.

［9］贾庆莲，乔彦峰，邓文渊.周视搜索系统对点目标的作用距离分析［J］.光学学报，2009，29（4）：937-943.