矩阵方程组AX=C，XB=D的行（列）共轭对称解

聂祥荣，王 珂，武玲玲

（1.贵州工程应用技术学院 数学系，贵州 毕节551700；2.上海大学 数学系，上海200444）

0 引 言

矩阵方程组是矩阵方程（组）理论与方法研究的重要对象，对研究其他类型矩阵方程（组）具有重要的基础性和方法性意义.式（1）的各种对称解是人们关注的课题之一，如文献［1-5］讨论了式（1）的Hermitian解、双对称解、中心对称解和P-对称解等.行（列）对称矩阵或行（列）对称延拓矩阵［6-8］在时频分布、信息、控制、建筑等具有轴对称特性现象中起着重要作用.最近，文献［9-11］利用奇异值分解和行对称矩阵的等价条件讨论了矩阵方程组（1）的行或列对称（延拓）解.

四元数矩阵特征值与特征向量问题由于四元数乘法的不可交换性变得较为复杂.许多学者对四元数矩阵右（左）特征值与特征向量做了大量有益的研究工作［12-18］，其中文献［12-13，18］利用四元数矩阵复表示矩阵的特征多项式（拟特征多项式）和重特征多项式，通过右复特征主值，描述了四元数矩阵全部右特征值的集合、给出了相应的求解右特征值的一个特征向量的方法.研究发现，可以通过复矩阵方程组（1）的具有行（列）共轭对称性的解获得四元数矩阵属于右特征值的全部特征向量.因此，为丰富矩阵方程组特殊解及其应用的研究内容，本文提出复数域上行（列）共轭对称矩阵概念，利用复矩阵的实表示和广义逆方法，讨论复数域上矩阵方程组（1）的行（列）共轭对称解，建立其存在行（列）共轭对称解的充分必要条件及该类解的一般表达式，并利用所得结果给出四元数矩阵右特征值的特征向量集合.

文中用Rm×n，Cm×n和Qm×n分别表示实数域、复数域和四元数体上的全体m×n阶矩阵.对于A∈Qm×n，AT，¯A，A＊，A†和r（A）分别表示矩阵A的转置、共轭、共轭转置、M-P逆和秩.I表示具有相应阶数的单位矩阵，Jm=（Ji，j）∈Cm×m（除J1，m=J2，m-1=…=Jm，1=1外其余元素均为零）.记LA=I-A†A，RA=I-AA†.

定义1 一个2n行（或2n+1行）矩阵X∈C2n×p（或X∈C（2n+1）×p）称为行共轭对称，是指存在Y∈Cn×p（或存在Y∈Cn×p，Γ∈R1×p）使得X=

定义2 一个2p列（或列2p+1）矩阵X∈Cn×2p（或X∈Cn×（2p+1））称为列共轭对称是指，存在Y∈Cn×p（或存在Y∈Cn×p，Γ∈Rn×1）使得X=［Y ¯YJp］（或X=［Y Γ ¯YJp］）.

1 复矩阵的实表示及有关引理

设矩阵A=A1+i A2∈Cm×n，其中A1，A2∈Rm×n.分别称矩阵

为A的行型和列型实表示矩阵.容易验证，矩阵A的行型和列型实表示矩阵具有如下性质

引理1［19］设A∈Cm×n，B∈Cm×k，C∈Cl×n，则下列秩等式成立

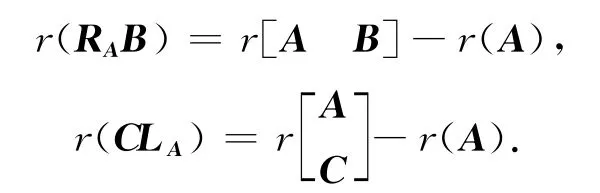
引理2［2］设A∈Cm×n，B∈Cp×q，C∈Cm×p，D∈Cn×q已知，而X∈Cn×p未知.则下列陈述等价：

1）矩阵方程组（1）可解；

2）RAC=0，DLB=0，AD=CB；

当式（1）可解时，其通解为

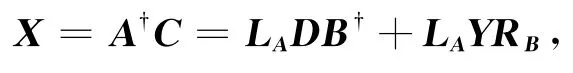
其中，Y是复数域C上任意具有适当阶数的矩阵.

2 矩阵方程组（1）的行共轭对称解

定理1 A∈Cm×2n，B∈Cp×q，C∈Cm×p，D∈

C2n×q已知，而X∈C2n×p未知.记

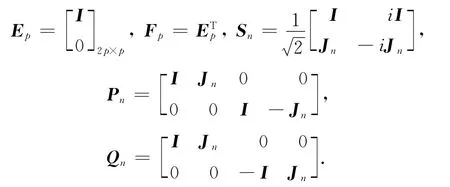
则下列陈述等价：

1）矩阵方程组（1）存在行共轭对称解；

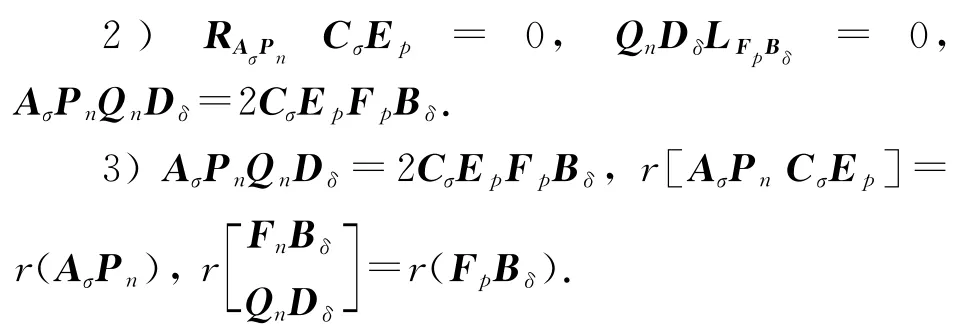
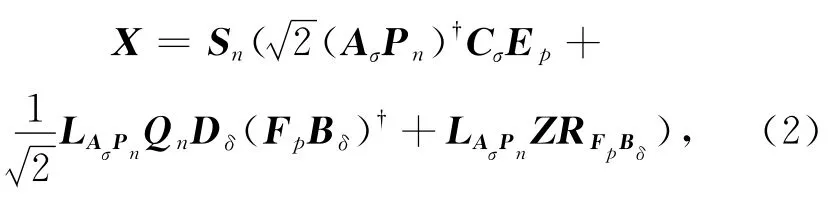
在上述情况下，式（1）的行共轭对称解的一般表达式为一般表达式为式（2）.设其中是式（1）的行共轭对称解.记则将X代入式（1），注意到［I i I］CσEp，可得

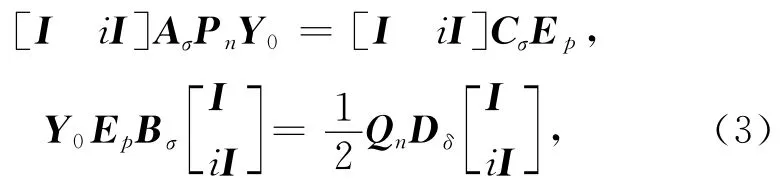
即

将引理2应用于实矩阵方程组（4）可得2）成立，且

式中：Z是实数域R上任意具有适当阶数的矩阵.从而X可表为式（2）.

当未知矩阵X为2n+1行时，令列陈述等价：

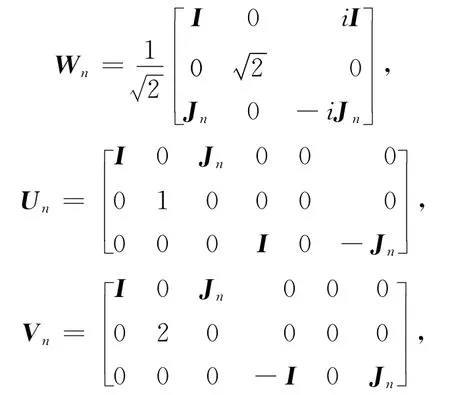
1）矩阵方程组（1）存在行共轭对称解；

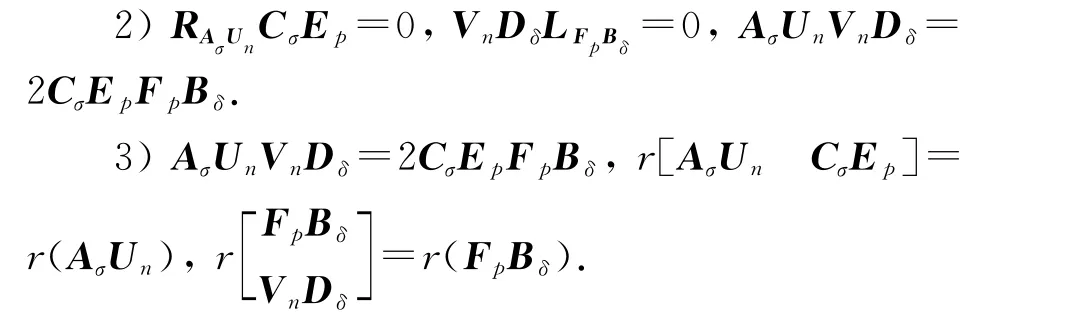
在上述情况下，式（1）的行共轭对称解的一般表达式为

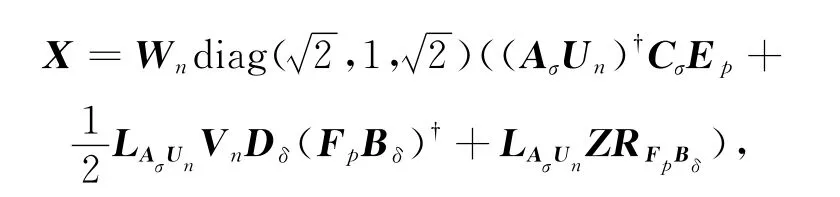
式中：Z是实数域R上任意具有适当阶数的矩阵.

备注 定理1（定理2）中等价条件2）和3）均为实形式.易验证Sn和Wn均是酋矩阵，即式（1）的行共轭对称解可分别通过行酋变换Sn（Wn）与实矩阵等价.

3 矩阵方程组（1）的列共轭对称解

由于矩阵方程组（1）等价于

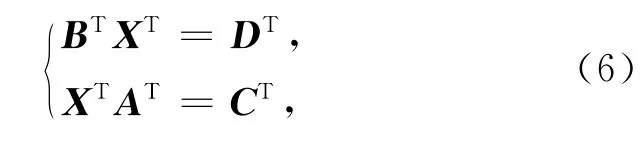
所以式1对未知矩阵X存在列共轭对称解X=［Y ¯YJp］（或X=［Y Γ ¯YJp］）等价于式（6）对XT存在行共轭对称解XT.将定理1（或定理2）应用于关于XT的式（6），并对所得矩阵等式、秩等式和XT的表达式两边转置，注意复矩阵实表示的性质，可得矩阵方程组（1）的两种列共轭对称解.

定理3 设A∈Cm×n，B∈C2p×q，C∈Cm×2p，D∈Cn×2p已知，而X∈Cn×2p未知.则下列陈述等价：

1）矩阵方程组（1）存在列共轭对称解；

式中：Z是实数域R上任意具有适当阶数的矩阵.

定理4 设A∈Cm×n，B∈C（2p+1）×q，C∈式中：Z是实数域R上任意具有适当阶数的矩阵.

证明 由引理1易知，2）与3）等价.因此只需证明1）与2）等价，且式（1）的行共轭对称解的Cm×（2p+1），D∈Cn×q，而X∈Cn×（2p+1）未知.则下列

陈述等价：

1）矩阵方程组（1）存在列共轭对称解；

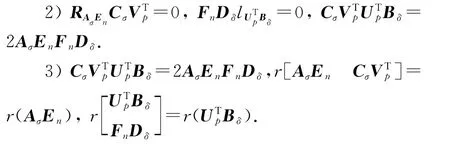
在上述情况下，式（1）的行共轭对称解的一般表达式为

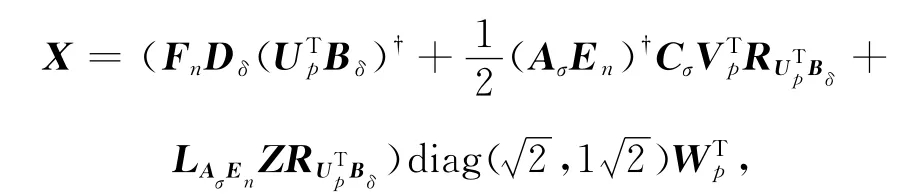
式中：Z是实数域R上任意具有适当阶数的矩阵.

4 四元数矩阵的右特征向量

根据文献［12-13，18］，A∈Qn×n的右特征值集合为｛qαq-1|0≠q∈Q，α是Aφ的复特征值｝.利用定理1的特殊情形AX=C的行共轭对称解，可得四元数矩阵右特征值的特征向量集合：

定理5 设A=A1+A2j∈Qn×n，A1，A2∈Cn×n，λ=λ1+λ2j∈Q（其中λ1，λ2∈C）是A的右特征值，则A的属于λ的特征向量集合为

根据定理1，存在Z0∈R4n×1，使得所以

为

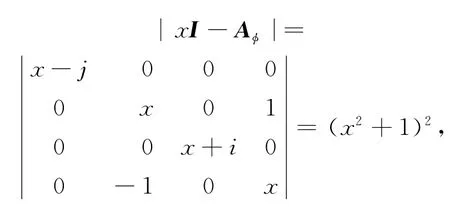
所以x=i是A的右复特征值，从而λ=（1+k）i·（1+k）-1=j是A的右特征值.由λ1=0，λ2=1得

所以

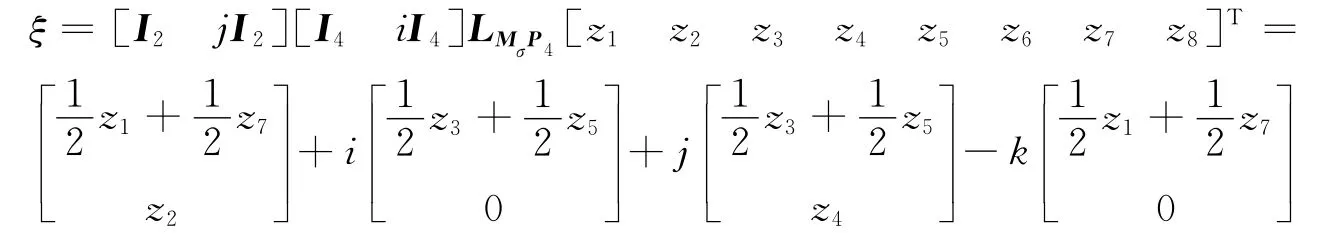
是A的右特征值λ=j的全部特征向量，其中，zj∈R，t=1，2，…，8，且或者z2≠0，或者z4≠0，或者z1≠-z7，或者z3≠-z5.

备注 如果考虑文献［13］定义3.5.4中的左特征值λ（满足ξA=λξ，ζ≠0），类似地利用定理2的特殊情形XB=D的列共轭对称解，可得四元数矩阵属于该类左特征值的特征向量集合.

［1］Khatri C G，Mitra S K.Hermitian and nonnegative definite solutions of linear matrix equations［J］.J.SIAM J.Appl.Math.，1976，31：579-585.

［2］Wang Qingwen，Yu Juan.On the generalized bi（skew-）symmetric solutions of a linear matrix equation and its procrust problems［J］.J.Applied Mathematics and Computation，2013，219：9872-9884.

［3］Wang Qingwen.Bisymmetric and centrosymmetric solutions to systems of real quaternion matrix equations［J］.J.Comput.Math.Appl.，2005，49：641-650.

［4］Li Y T，Wu W J.Symmetric and skew-antisymmetric solutions to systems of real quaternion matrix equations［J］.J.Comput.Math.Appl.，2008，55（6）：1142-1147.

［5］Zhang Qin，Wang Qingwen.The（P，Q）-（skew）symmetric extremal rank solutions to a system of quaternion matrix equations［J］.J.Applied Mathematics and Computation，2011，217：9286-9296.

［6］袁晖坪.行（列）对称矩阵的奇异值分解［J］.中北大学学报（自然科学版），2009，30（2）：100-104.Yuan Huiping.Singular value decomposition of row（column）symmetric matrix［J］.Journal of North Univeristy of China（Natural Science Edition），2009，30（2）：100-104.（in Chinese）

［7］邹红星，王殿军，戴琼海，等.延拓矩阵的奇异值分解［J］.科学通报，2000，45（14）：1560-1562.Zou Hongxing，Wang Dianjun，Dai Qionghai，et al.SVD for extended matrix［J］.Chinese Science Bulletin，2000，45（14）：1560-1562.（in Chinese）

［8］邹红星，王殿军，戴琼海，等.行（或列）对称矩阵的QR分解［J］.中国科学（A辑），2002，32（9）：842-849.Zou Hongxing，Wang Dianjun，Dai Qionghai，et al.QR factorization for row or column symmetric matrix［J］.Science of China（Series A），2002，32（9）：842-849.（in Chinese）

［9］吴强，吴霞.列延拓矩阵方程组的最佳逼近解［J］.暨南大学学报（自然科学版），2013，34（3）：267-269.Wu Qiang，Wu Xia.The optimal approximations of the equations of column extended matrix［J］.Journal of Jinan University（Natural Science），2013，34（3）：267-269.（in Chinese）

［10］吴强.行延拓矩阵的矩阵方程组的最佳逼近解［J］.科技通报，2012，28（2）：13-17.Wu Qiang.The optimal approximation solution to the matrix equations of line extended matrix［J］.Bulletin of Science and Technology，2012，28（2）：13-17.（in Chinese）

［11］刘桂香.AX=B的行（反）对称与列（反）对称解［J］.扬州职业大学学报，2013，17（2）：25-28.Liu Guixiang.On the solutions to row（skew）symmetric and column（skew）symmetric for AX=B［J］.Journal of Yangzhou Polytechnic College，2013，17（2）：25-28.（in Chinese）

［12］李文亮.四元数矩阵［M］.长沙：国防科技大学出版社，2002.

［13］庄瓦金.体上矩阵理论导引［M］.北京：科学出版社，2006.

［14］Zhang Fuzhen.Quaternions and matrices of quaternions［J］.Linear Algebra Appl.，1997，251：21-57.

［15］Farid F O，Wang Qingwen，Zhang Fuzhen.On the eigenvalues of quaternion matrices［J］.Linear and Multilinear Algebra，2011，59（4）：451-473.

［16］Huang Liping，Wasin So.On left eigenvalues of a quaternionic matrix.Linear Algebra and its Applications［J］，2001，323：105-116.

［17］Andrew B.Right eigenvalues for quaternionic matrices：a topological approach［J］.Linear Algebra and its Applications，1999，286：303-309.

［18］陈龙玄.四元数矩阵的特征值和特征向量［J］.烟台大学学报（自然科学与工程版），1993（3）：1-8.Chen Longxuan.The characteristic value and its vector of quaternion matrix［J］.Journal of Yantai University（Natural Science and Engineering），1993（3）：1-8.（in Chinese）

［19］Wang Qingwen，Li Chengkun.Ranks and the leastnorm of the general solution to a system of quaternion matrix equations［J］.J.Linear Algebra Appl.，2009，430：1626-1640.