基于L-BFGS与NSGA-Ⅱ混合算法的IMRT逆向计划优化研究
2015-12-02桂志国
杨 婕,桂志国
(1.中北大学 电子测试技术国家重点实验室,山西 太原030051;2.山西中医学院 医药管理学院,山西 太原030619)
0 引 言
调强放射治疗(Intensity Modulation Radia-tion Therapy,IMRT)被誉为21世纪放射治疗发展的方向,是目前治疗恶性肿瘤的主要手段之一.它通过调节照射肿瘤靶区(Planning Target Vol-ume,PTV)射线束的强度,使得靶区接受的剂量最大,靶区周围危及器官(Organ At Risk,OAR)和正常组织(Normal Tissues,NT)接受的剂量最小,从而提高治疗增益比,改善病人生存质量.逆向计划是IMRT的关键环节,其主要过程是依据医生给出PTV处方剂量和OAR耐受剂量,综合考虑各种因素确定优化目标函数,再由计算机通过各种优化算法计算每个射野的最佳射束强度分布,最终得到较优的治疗计划.逆向计划的质量直接影响到治疗的精度和疗效.
IMRT逆向计划中优化目标函数分为物理目标函数和生物目标函数.物理目标函数描述的是处方剂量与所计算剂量分布之间的差值,如平均剂量函数、最小剂量函数、最大剂量函数和剂量-体积(Dose-Volume,DV)准则等[1].生物目标函数描述的是方案治疗效果,是肿瘤或正常组织内的非线性放射生物效应,如等效均一剂量(Equivalent Uniform Dose,EUD)、肿瘤控制率(Tumor Control Probability,TCP)和正常组织并发症发生概率(Normal Tissue Complication Probability,NTCP).物理目标函数的具有定义简单,便于应用的优点,但具有一定的局限性,不能准确地预测肿瘤或正常组织内的非线性放射生物效应,生物目标函数已成为一种替代物理目标函数的选择[2].有文献[3-5]表明,生物目标函数可以得到更好的剂量分布.
IMRT逆向计划优化方法分为单目标法和多目标法.单目标法是将多个优化目标通过加权求和化为单一函数再使用成熟算法优化,如L-BFGS(Limited Memory BFGS)算法.该方法的优点是收敛速度较快,优化时间短;缺点是对于非凸函数得到的可能是局部极值,各目标函数的权重赋值是个反复试误(Trial and Error)的过程[6],每次计算只能得到一个优化解.多目标法是采用进化算法直接进行优化,如NSGA-Ⅱ(Non-Dominated Sorting Genetic Algorithm-Ⅱ)算法.其优点是一次计算就可以得到Pareto最优解集合,具有更好的灵活性,缺点是响应时间长,收敛速度慢等.
针对上述情况,本文将物理-生物混合目标函数引入到IMRT逆向计划中,利用L-BFGS算法对NSGA-Ⅱ算法进行加速,并对NSGA-Ⅱ算法的快速非支配排序策略进行了修改.将本文算法与单一物理目标和其他优化方法在10名前列腺肿瘤患者中进行了对比实验.实验结果表明,利用新算法所得放射治疗计划质量更高,所需计算时间更短.
1 本文方法
逆向计划优化的目的是得到最佳的放疗方案,在对靶区产生不可恢复性摧毁的同时保护周围关键组织和正常组织.为了得到更好的放疗方案,本文对常见优化算法[7-11]进行了深入研究,在此基础提出一种新算法.首先确定物理-生物的混合目标函数,以物理函数最小-最大剂量函数控制靶区的剂量分布,以物理函数DV准则和生物函数广义EUD(generalized EUD,gEUD)[12]控制危及器官的剂量分布.然后仅选择靶区和危及器官的平均剂量函数作为优化目标简化混合优化目标,利用L-BFGS对其优化.将L-BFGS优化所得到的解与随机生成的值合并作为NSGA-Ⅱ的第一代种群.最后利用NSGA-Ⅱ优化混合目标函数,得到多个剂量分布方案供临床使用.
1.1 混合优化目标函数
通常逆向计划优化采用的是物理函数目标,计算每个体素剂量值与处方剂量差的平方,但其不能准确反映器官组织受到不均匀剂量照射时的生物效应.因此为了保证放射治疗计划的质量,本文在逆向计划中提出一种带约束的物理-生物混合目标函数:使用最小-最大剂量函数fmin-max(D)作为约束条件控制PTV的剂量,确保靶区的高剂量分布;利用DV准则函数fDV(V50)作为约束条件控制危及器官内剂量达到50 Gy的体积;利用gEUD函数fgEUD(D)和DV准则函数fDV(V75)作为目标函数,尽量降低危及器官内平均剂量和高剂量的分布.其数学模型如下

式中:Di为第i个体素的剂量值;N为器官组织内的所有体素点;α(-∞≤α≤+∞)为剂量体积效应因子,靶区组织的α≤1,正常组织的α>1;TD5/5是危及器官最小耐受剂量;V75指器官组织内接收到剂量75 Gy的体积;Dmean为靶区处方剂量或正常组织的平均耐受剂量;Cd是适当放宽靶区剂量的指数;V50指器官组织内接收到剂量50 Gy的体积;Vmax%指DV约束中对应的体积上限.
由于DV准则函数和gEUD函数不是凸函数,求导过程较复杂,为了便于后期使用L-BFGS算法优化,本文将上述混合模型简化,将其改为只含有平均剂量函数的无约束优化目标函数.数学模型如下
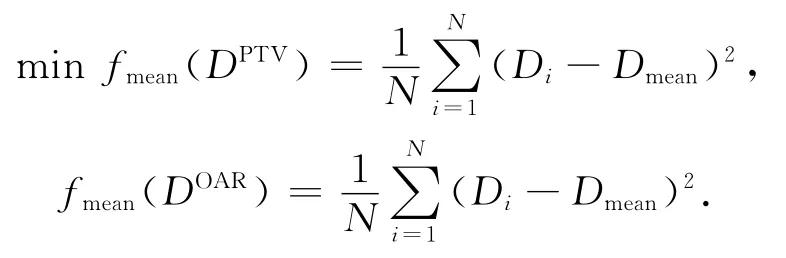
1.2 混合优化算法
逆向计划优化常见算法分为确定型和概率型,其中具有代表性的是L-BFGS算法和NSGA-Ⅱ算法.L-BFGS算法是BFGS算法的改进,是拟牛顿法优化算法的一种,属于确定型算法.其采用目标函数的一阶梯度信息构造一系列的正定矩阵逼近大规模的Hessian矩阵,从而在计算复杂度和存储空间都有明显降低,适合求解大规模的优化问题.NSGA-Ⅱ算法是NSGA的改进,属于进化算法的一种,属于概率型算法.其通过增加精英保留策略、密度估计策略和快速非支配排序策略,改善了NSGA算法的缺点.它以在解决多目标优化问题时的优良性得到人们的广泛关注.
优化目标函数时,如果单一使用L-BFGS算法首要需要解决的问题就是对目标函数求导,而逆向计划优化中大部分函数都是非凸的,其求导过程较复杂;如果单一使用NSGA-Ⅱ算法直接优化,又存在由于变量维数过高得不到满意解和响应时间过长的问题.因此,本文将两种算法进行混合,先以L-BFGS算法对简化的凸函数优化目标函数进行优化,再以NSGA-Ⅱ算法对全部目标函数进行优化.主要流程如下
Stepl:输入CT数据;
Step2:判断是否运行L-BFGS算法5次,满足则跳转到Step5,否则执行Step3;
Step3:确定优化函数;
Step4:运行L-BFGS算法优化目标函数f,得到优化解,并保存至数组X;
Step5:确 定 多 目 标 优 化 函 数,fgEUD(DOAR)和fDV(VOAR75),约束条件为fmin-max(DPTV)和fDV(VOAR50);
Step6:随机产生NSGA-Ⅱ算法295个初始解,并与X合并;
Step7:运行NSGA-Ⅱ算法优化目标;
Step8:得到Pareto解集,结束.
本文需采用L-BFGS算法优化的目标函数只有平均剂量函数,给出其一阶导数.
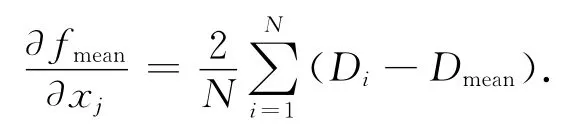
本文采用NSGA-Ⅱ算法优化的混合目标,将fmin-max(DPTV和fDV(VOAR50)作为约束条件.
逆向计划优化过程属于带约束的多目标优化问题.NSGA-Ⅱ算法在处理约束条件时是将约束条件改成目标函数进行优化,得到优化解后再通过决策挑选出适用解,这样无疑加大了优化的工作量.因此本文对NSGA-Ⅱ算法的快速非支配排序策略进行了改动,假设a和b是两个解,在判断其是否为非劣解时首先要求满足约束条件,再判断目标函数最小值.具体改动为

2 实验及结果分析
为了验证算法有效性,本文对10例前列腺肿瘤病人的实际数据,分别使用混合目标混合优化法(M-M)、物理目标混合优化法(S-M)、混合目标单一NSGA-Ⅱ法(M-S)和混合目标无约束混合法(M-NM)进行了对比实验,并利用DVH图、TCP[13]、NTCP[13]和HI[14]指数对不同方案优化算法的结果进行了评价.
器官组织CT(见图1)由患者仰卧位采取.PTV为前列腺,OAR1是直肠(Rectum),OAR2是膀胱(Bladder).
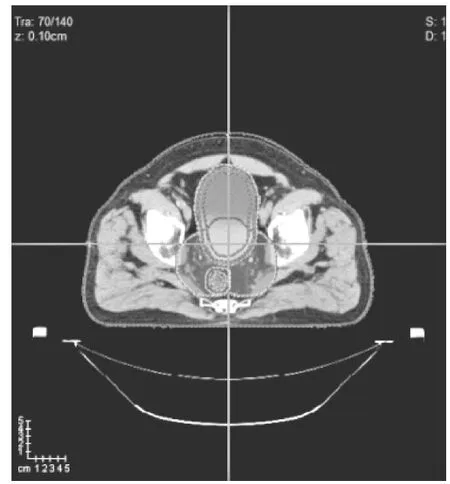
图1 盆腔器官组织CT Fig.1 CT of pelvic organs
CERR开源软件采用5个6 MeV共弧面照射靶目标,机架角度依次为:36°,100°,180°,260°,324°,勾画PTV和OAR得到剂量效应矩阵.
L-BFGS优化目标函数为f(D)=ζ1·fmean(DOAR2)+ζ2fmean(DOAR1+ζ3fmean(DPTV),靶区的均匀处方剂量为78 Gy,危及器官膀胱和直肠的耐受剂量设定为最小耐受剂量TD5/5:60 Gy,60 Gy.ζi是服从[0,1]的随机数,并做归一化处理.
NSGA-Ⅱ优 化 目 标 函 数 为fgEUD(DOAR2),fgEUD(DOAR1),fDV(VOAR275)和fDV(VOAR175).约束条件为fmin-max(DPTV),fDV(VOAR250)和fDV(VOAR150).其中靶区处方剂量为78 Gy,危及器官受到的g EUD为60 Gy,gEUD模型中直肠和膀胱α取值分别为8和8[15-16].约束条件是VOAR150%=50%,VOAR150%=50%,Cd=2.
本文对比实验所使用的方案均在MATLAB平台上编程实现.NSGA-Ⅱ算法种群规模为300,进化代数为600,变异率0.1,交叉率为[0,1]上的随机数.第一代父代种群中,包括5组L-BFGS算法得到的优化解,及295组随机数.
2.1 与单一物理目标的对比
在一例前列腺肿瘤患者上测试了本文目标与物理目标对优化结果的影响.物理目标选择为fmax(DOAR2),fmax(DOAR1),fDV(VOAR275)和fDV(VOAR175).约束条件为fmin-max(DPTV),fDV(VOAR250)和fDV(VOAR150).其中fmax(D)函数定义如下

式中:DmaxO危及器官的耐受剂量.优化设置靶区均匀剂量为78 Gy,危及器官接受剂量为60 Gy.其他设置同混合目标相同.两种目标函数均采用本文混合算法优化.
优化结果如图2所示,图2(a)是采用M-M法优化得到的所有DVH曲线图,图2(b)是采用S-M法优化得到的所有DVH曲线图,不同线型分别对应靶区、直肠和膀胱.从图中可以看出,采用混合目标函数得到的靶区剂量分布更加均匀,即有90%的靶区达到最小剂量74 Gy,且最大剂量不超过处方剂量的110%(85.8 Gy).但对于单一物理目标函数,剂量上限超过了85.8 Gy,存在热点,影响了治疗效果.图2(c)为分别选择两个优化目标得到结果中TCP指数最高的一组对比,可以看出在确保PTV高剂量的同时,混合目标函数明显降低了ORA内高剂量的分布.同时与表1危及器官的DV约束准则进行比较,混合目标所得到的DVH曲线在高剂量区域更加符合要求.
分别计算两种目标函数优化后得到数据的TCP、NTCP及HI,选择其中TCP较高的前5项.数据见表2.从表中可以看出由于两种目标函数均使用fmin-max(DPTV)作为约束条件,因此所得到的TCP和HI指数几乎相同,但用单一的物理目标函数与混合目标函数相比,其对危及器官高剂量分布的控制较差,直肠和膀胱的NTCP均有增大,尤其是直肠更加明显.可见本文提出的混合优化函数,加入了g EUD生物目标函数,在TCP相同的情况下,NTCP有了明显降低,更好地保护了危及器官,治疗效果更好.
本文在10例前列腺肿瘤患者中测试了混合目标与单一物理目标对优化结果的影响.分别计算两种目标函数优化后得到数据的TCP、NTCP及HI,每个病例均选择TCP最大的一组数据,结果见表3.表中结果表明混合目标对于不同的病人在TCP没有减少的情况下,NTCP均有略微下降.

图2 不同的目标函数在一例前列腺患者上所得结果 Fig.2 Results of patients with prostate using different objective function

表1 危及器官的DV约束条件 Tab.1 DV constraint conditions for endanger organs

表2 混合目标函数和单一物理目标函数在一例前列腺患者上所得TCP、NTCP和HI值 Tab.2 TCP,NTCP and HI values obtained from the mixed objective function and a single physical target function in the same patient with prostate

表3 混合目标函数和单一物理目标函数在10例前列腺患者上所得TCP、NTCP和HI值 Tab.3 TCP,NTCP and HI values obtained from the mixed objective function and a single physical target function in 10 patients with prostate
2.2 与单一NSGA-Ⅱ算法和无约束混合算法的对比
在同一例前列腺肿瘤患者上,使用相同的混合目标分别测试了M-M、M-S和M-NM.M-M参数设置与上文相同.M-S参数设置为种群300,遗传代数600,变异率0.1,交叉率为[0,1]上的随机数.M-NM将混合目标中的约束条件转换为优化目标函数,参数设置为种群300,遗传代数600,变异率0.1,交叉率为[0,1]上的随机数,L-BFGS算法参数设置同M-M算法设置.优化结果见图3.图3(a)是M-M优化得到的所有DVH曲线图,图3(b)是M-S优化得到的所有DVH曲线图,图3(c)是M-NM优化得到的所有DVH曲线图.图3(d)为分别选择三组优化结果中TCP指数最高的一组对比.

图3 不同的优化法在一例前列腺患者上所得结果 Fig.3 Results of different optimization methods used a patient with prostate
从图3中可以看出,相比单一NSGA-Ⅱ算法,在相同的种群和迭代次数设置下,混合算法能快速得到理想的DVH曲线,保证靶区的剂量分布,而单一NSGA-Ⅱ算法,靶区高剂量分布达不到90%的覆盖率.而与无约束混合算法相比,相同的靶区分布下,危及器官内高剂量的分布更少.因此,本文提出的混合算法优化效率更高.在新算法中,虽然需要事先使用梯度算法优化目标函数,但优化目标已简化,因此计算时间并无明显增加.
3 结 语
本文提出了一个新的逆向计划优化算法.先构造了一个基于物理-生物准则并带有约束条件的混合优化目标.再使用混合算法进行优化.为了验证新算法的有效性,本文算法在10例前列腺肿瘤患者上与基于物理准则的优化目标、单一优化算法和无约束优化算法进行了对比实验.从大量的实验数据中,可以看出,混合目标混合优化算法,可以在确保靶区剂量均匀分布的前提下,降低危及器官内的剂量分布,提高优化质量.同时,新算法避免了权值的选择,并一次得到多个DVH曲线,医生可以具体要求进行个性化选择,提高了临床治疗的灵活度,具有较好的可行性.但由于优化目标函数和变量较多,在加速的情况下优化时间仍较长.下一步将继续尝试为优化算法加速.
[1]Wu Q,Mohan R,Niemierko A,et al.Optimization of intensity-modulated radiotherapy plans based on the equivalent uniform dose[J].Int J Radiat Oncol Biol Phys,2002,52(1):224-235.
[2]Stavrev P,Hristov D,Warkentin B,et al.Inverse treatment planning by physically constrained minimization of a biological objective function[J].Med Phys,2003,30(11):2948-2958.
[3]Li A X,Alber M,Deasy J O,et al.The use and QA of biologically related models for treatment planning:short report of the TG-166 of the therapy physics committee of the AAPM[J].Med Phys,2012,39(3):1386-1409.
[4]Dirscherl T,Alvarez-Moret J,Bogner L.Advantage of biological over physical optimization in prostate cancer[J].Z Med Phys,2011,21(3):228-235.
[5]Diot Q,Kavanagh B,Timmerman R,et al.Biological-based optimization and volumetric modulated arc therapy delivery for stereotactic body radiation therapy[J].Med Phys,2012,39(1):237-245.
[6]Langer M,et al.Comparison of mixed integer programming and fast simulated annealing for optimizing beam weights in radiation therapy[J].Med.Phys.,1996,23:957-964.
[7]林琳.IMRT逆向计划中多目标优化算法进化策略的研究[D].浙江:浙江工业大学,2009.
[8]盛大宁.IMRT逆向计划中的混合多目标梯度算法研究[D].安徽:合肥工业大学,2010.
[9]闵志方,宋恩民,金人超,等.用于逆向计划设计的整合优化方法[J].华中科技大学学报(自然科学版),2010,38(1):5-8.Min Zhifang,Song Enmin,Jin Renchao,et al.Integrated optimization method to design inverse planning[J].Journal of Huazhong University of Science and Technology(Nature Science Edition),2010,38(1):5-8.(in Chinese)
[10]Daly-Schveitzer N,Juliéron M,Gan Tao Y,et al.Intensity-modulated radiation therapy(IMRT):Toward a new standard for radiation therapy of head and neck cancer[J].European Annals of Otorhinolaryngology,Head and Neck Diseases,2011,128(5):241-247.
[11]Kondoh T,Kashima H,Yang J F,et al.Dynamic optical modulation of an electron beam on a photocathode RF gun:Toward intensity-modulated radiation therapy(IMRT)[J].Radiation Physics and Chemistry,2008,77(10):1142-1147.
[12]Niemierko A.A generalized concept of equivalent uniform dose(EUD)(abstract)[J].Med Phys,1999,26(6):1110.
[13]Withers H R,McBride W H.Biologic basis of radiation therapy[M].Philadelphia:Lippincott-Raven,1998.
[14]Murshed H.Dose and volume reduction for normal lung using intensity-modulated radiotherapy for advanced-stage non-small-cell lung cancer[J].Int J Radiat Oncol Biol Phys,2004,58(4):1258-1267.
[15]Burman C,Kutcher G J,Emami B,et al.Fitting of normal tissue tolerance data to an analytic function[J].Int J Radiat Oncol Biol Phys,1991,21:123-135.
[16]Emami B,Lyman J,Brown A,et al.Tolerance of normal tissue to therapeutic irradiation[J].Int J Radiat Oncol Biol Phys,1991,21:109-122.
