某火炮高平机手轮力6σ稳健优化设计

张柳怡，顾克秋

（南京理工大学 机械工程学院，江苏 南京 210094）

随着火炮轻量化技术的发展，出现了新型组合结构的高低平衡机，简称高平机。高平机平衡部分产生的平衡力矩由蓄能器内的平衡气体产生。当平衡部分结构参数确定之后，高平机在各个射角状态下的平衡气体体积均为某一定值。在某一固定射角状态下，平衡气体的体积一定，而当工作环境的温度产生变化之后，蓄能器内气压即产生波动，平衡力将偏离理论值，引起不平衡力矩的变化，进而导致手轮力的不稳定。

温度的变化对高平机性能的影响直接体现在手轮力大小的波动。例如，60 式122 mm 加农炮，气温变化5℃，手轮力将增大20 N；59 式130 mm加农炮，气温变化10℃，手轮力将增大80 N。可见，工作环境温度的不确定性对高平机工作性能具有很大影响，但是火炮工作环境的温度无法人为控制。

高平机作为新型结构得到广泛的研究。吴迎春［1］提出液体气压式高平机方案并以最大不平衡力矩最小为优化目标进行优化。张训国［2］对螺杆气压式高平机进行优化设计，目标函数为最大不平衡力矩。王妍智［3］直接以最大手轮力最小为优化目标，对高平机系统进行整体优化。已有文献已将高平机平衡性能作为优化目标进行优化设计，但未考虑到不确定因素对平衡性能的影响。

传统的确定性设计方法无法定量评估不确定因素对设计目标的影响［4］。在本文中，温度就是一个不确定因素，笔者将稳健设计的思想应用于高平机的设计中，考虑温度波动对手轮力波动的影响。将温度作为不确定因素，并将这一不确定因素转化成对平衡腔气压设计变量的描述，对高平机进行稳健优化，降低手轮力对温度变化的敏感度，提高高平机的稳健性。

1 稳健优化基本原理

1.1 稳健设计

稳健设计法又称三次设计法，是使设计产品在制造和使用过程中，结构有关参数发生变化时，产品性能保持在稳定状态的一种设计方法。当产品性能的变化对于参数变化相对较小时，说明产品对该因素的变化具有稳健性［5］。一般说来，稳健设计要求达到的两个目的是：使产品质量特性的均值尽可能达到目标值；使由各种干扰因素引起的功能性波动的方差尽可能减小［6］。

1.2 稳健优化设计

稳健优化设计是用稳健设计方法来改善产品的技术性能，即在优化设计时达到稳健设计的两个目的。图1为稳健优化与确定性优化的对比图。确定性优化能得到可行范围内的最优解，当随机变量产生±Δx1的波动时，目标函数产生的波动±Δf1较大，而在稳健设计点，随机变量产生±Δx2的波动导致目标函数产生的波动±Δf2则较小［7］。

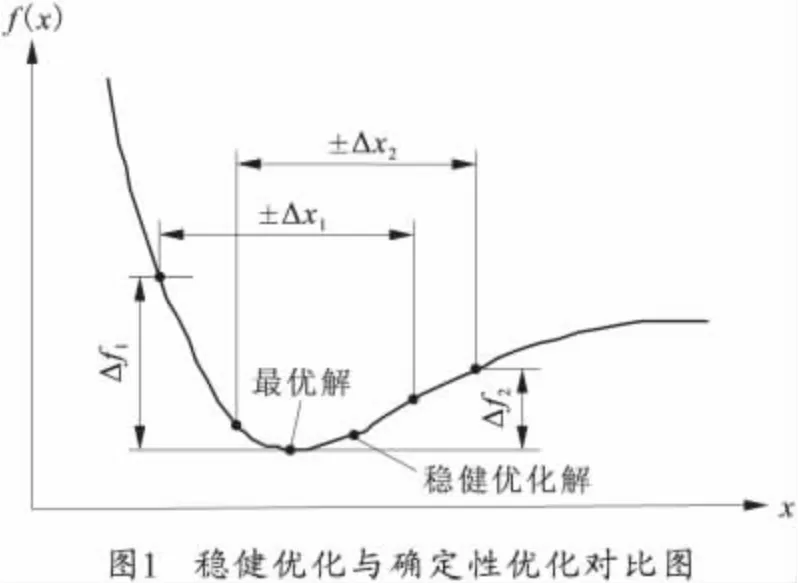
实际情况中存在不少不确定的影响因素，想要从根本上消除这些不确定影响因素是很难做到的，并且可能需要付出不小的代价。稳健优化设计主要是控制和减小目标函数的响应波动，降低在设计点上的敏感性，使得目标函数响应的均值达到目标，并且使得响应的标准差最小化。常用的稳健优化设计方法有田口设计和6σ稳健设计。相比之下，6σ稳健设计方法更易于构造问题，求解自动化程度高，质量的约束可以明确定义，故选择6σ稳健设计作为本次优化的理论依据。6σ稳健设计要求产品质量在均值6σ范围波动时，均满足设计要求，此时，产品可靠度达到99.999 999 8%。

确定性优化问题一般采用的数学模型为［8］：

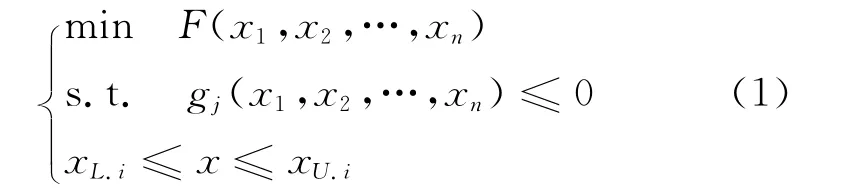
式中，xL.i、xU.i分别为变量xi的许用上下限。

稳健优化设计的数学模型为［9］：

式中：μxi、μy为随机变量xi和响应y的均值；σxi、σy为随机变量xi和响应y的标准差；gj为约束函数；xL.i、xU.i分别为变量xi的许用上下限；n为σ水平，当n＝6时称为6σ稳健设计。

与确定性优化方法相比，6σ稳健设计的目标函数中增加了目标函数和所有约束条件的标准差，目的在于寻求目标函数最优解的同时，也能降低目标函数对设计变量中不确定变量的敏感性［10］。

笔者以高平机手轮力最大值最小为优化目标，对其进行确定性优化，并对确定性优化结果进行稳健评估；利用6σ稳健设计模块对高平机结构进行稳健优化，并对稳健优化结果进行稳健评估；最后，依据二者的评估结果对两种优化方案进行对比分析。

2 影响平衡特性的不确定因素分析

在高平机工作过程中，工作环境气温的变化是不可避免的。在高平机射角为α时，高平机气体容积为V，初始设定压强为p1，对应的气体温度为T1。若在此射角，环境温度变为T2，则对应的气体压强将变为p2。

根据气态方程

式中：p为气体压强；V为气体体积；n为气体物质的量；R为普适气体常量；T为热力学温度。

可得：

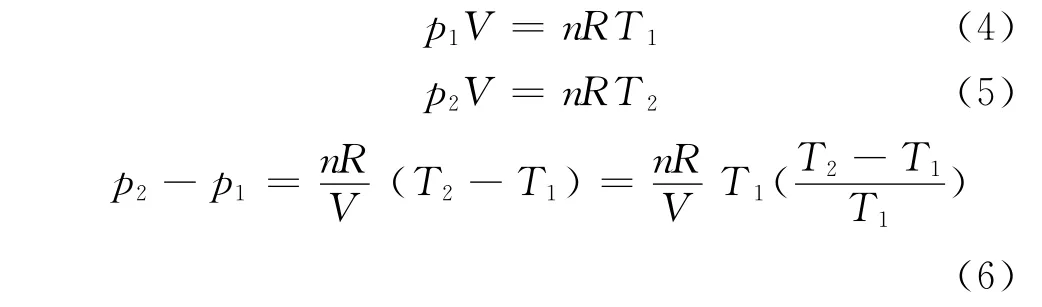
即：

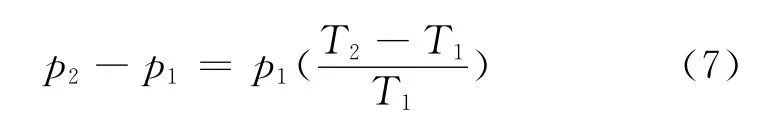
假设初始设定的工作温度为15℃，对应的热力学温度为288.15K，而实际气温在10～20℃之间波动，推出对应的热力学温度范围为283.15 ～293.15K。

可得：

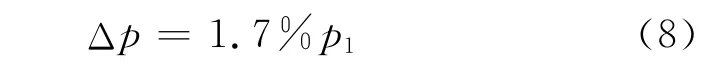
所以当温度在设定值上下波动范围为10℃，初压为8 MPa时，压强将产生0.3 MPa左右的波动，导致手轮力存在几十牛顿的波动。可见温度对高平机性能稳定的影响不容忽视。

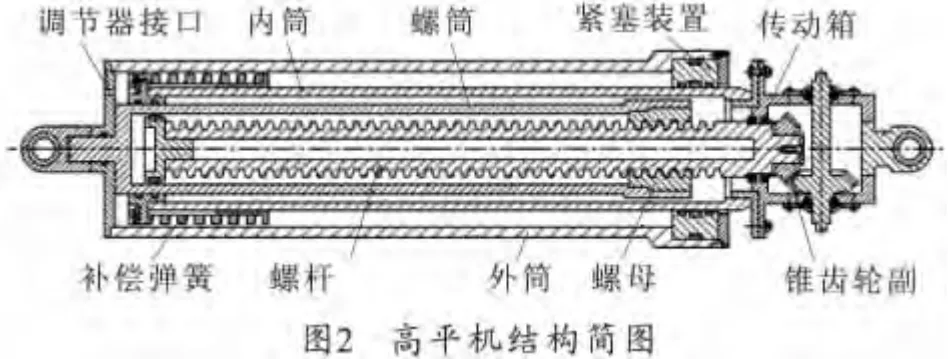
在对高平机进行稳健优化设计时，根据图2所示高平机结构，选取以下10个参数作为设计变量：高平机在最大射角时初始容积V、高平机最大射角时初始压强p、补偿弹簧刚度K、补偿弹簧工作起始角度β、螺筒外半径Rn、内筒外半径Rp、上支点相对耳轴坐标分量x1、y1，下支点相对耳轴坐标分量x2、y2。其中初压p作为不确定变量，根据不确定因素分析，参与优化时服从均匀分布，其余设计变量均为确定性变量。优化目的是通过稳健设计，使得手轮力对不确定变量初压p不敏感。

3 高平机6σ稳健优化设计

3.1 确定性优化

确定性优化以手轮力最大值Fmax最小为优化目标，将所有设计变量作为确定性变量，对高平机结构进行确定性优化。采用多岛遗传算法，经过10 000次仿真计算，得到的优化结果如表1所示。

表1 高平机确定性优化方案表

由给出的高平机结构，推导出针对该结构的手轮力计算公式，将确定性优化得到的参数结果，代入该高平机手轮力计算公式［3］，得到手轮力最大值为107.8N。

3.2 确定性优化结果稳健性评估

对确定性优化方案的评估，利用Isight提供的6σ稳健设计模块，将初始压强p作为随机变量。由不确定因素分析可推出，p服从均匀分布，分布范围为［6.64，6.88］，其余参数设定为确定性参数，最大手轮力Fmax目标约束设置为不大于150N。对p通过随机抽样，获得手轮力最大值Fmax在分布气压下分布均值为133.397N，标准差为15.44N，σ水平为1.347。其概率分布如图3所示。

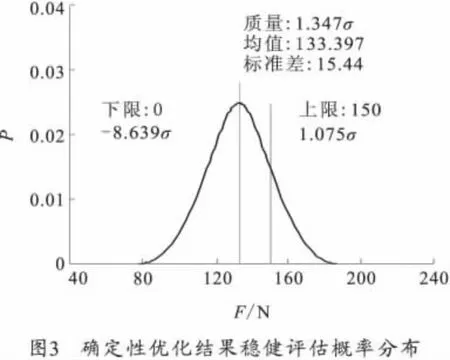
3.3 稳健优化

本次优化过程中，优化参数与确定性优化相同，其中将初压p作为服从均匀分布的随机变量，其余参数作为确定性变量。

本次优化实质为多目标优化，3个分目标分别为标准气压下最大手轮力Fmax、最大手轮力Fmax在分布气压作用下分布的期望μFmax与标准差σFmax，通过线性加权，构成稳健优化的目标函数。通过设置权重因子来调整这3 个分目标在优化结果中的重要性。得到的优化结果如表2所示。

表2 高平机稳健优化方案表

其中，p的设定值为6.95 MPa，其分布范围为［6.84，7.08］。

3.4 稳健优化结果校核

根据优化后方案的参数，代入高平机手轮力计算公式，得到设定气压下最大手轮力Fmax为117.7 N。对p通过蒙特卡罗抽样方法进行1 000次随机抽样，获得手轮力最大值Fmax在分布气压作用下分布的均值为129.45N，标准差为9.555N，σ水平为8。其概率分布如图4所示。

6σ稳健优化后，可以看出Fmax的期望值有所减小，一定程度体现了手轮力整体大小得到降低；Fmax的标准差有所减小，即优化后Fmax的波动减小，稳健性得到改善；σ水平由1.347提高到8，即F小于150N 的可靠度由82.2%提高到100%。

4 特殊点验证

本次稳健优化设计中，优化目标为最大手轮力最小，对于几个特殊角度手轮力的稳健性并未做出明确阐述。故将通过具体手轮力计算，改变压强，使压强的变化达到最大限度，观察这些角度手轮力F对压强变化的敏感程度是否有降低。

4.1 稳健优化前手轮力变化情况

根据分析，压强在假设温度的变化情况下，会产生上下各1.7%的波动。故模拟温度变化产生的压强波动的数值组为6.64、6.70、6.76、6.82、6.88 MPa。由优化前手轮力曲线图可知，手轮力F大小存在几个波峰分别在由高射角向低射角调炮至射角－3°、43°、65°，由低射角向高射角调炮至射角18°、57°。选取这几个角度作为特殊点，命名为A点、B点、C点、D 点、E点。模拟的手轮力数值如表3所示。

表3 确定性优化手轮力数值模拟表

4.2 稳健优化后手轮力变化情况

经过稳健性优化之后，参数发生了改变，模拟温度变化产生压强波动的数值组变为6.84、6.90、6.96、7.02、7.08 MPa。根据优化后手轮力曲线图，同样选取手轮力F的几个波峰位置，分别在由高射角向低射角调炮至射角－3°、44°、65°，由低射角向高射角调炮至射角19°、56°。分别选取这几个角度作为稳健优化后特殊点加以验证。模拟的手轮力数值如表4所示。

表4 稳健优化手轮力数值模拟表

稳健优化前后模拟温度变化，手轮力数值与设定温度下手轮力变化值对比如表5所示。由数据可知，优化后的高平机在名义压强下的手轮力虽然最大值相比确定性优化方案有所提高，但是增大的数值在可接受范围内；并且，在最大压强情况下，稳健优化后的最大手轮力比确定性优化方案的最大手轮力有所降低。由表5可以直观地看出，随温度变化相同幅度，在各特殊点手轮力的变化值在稳健优化后均有减小。

取A 点作为观测点，作其手轮力随着压强变化曲线图，如图5所示。

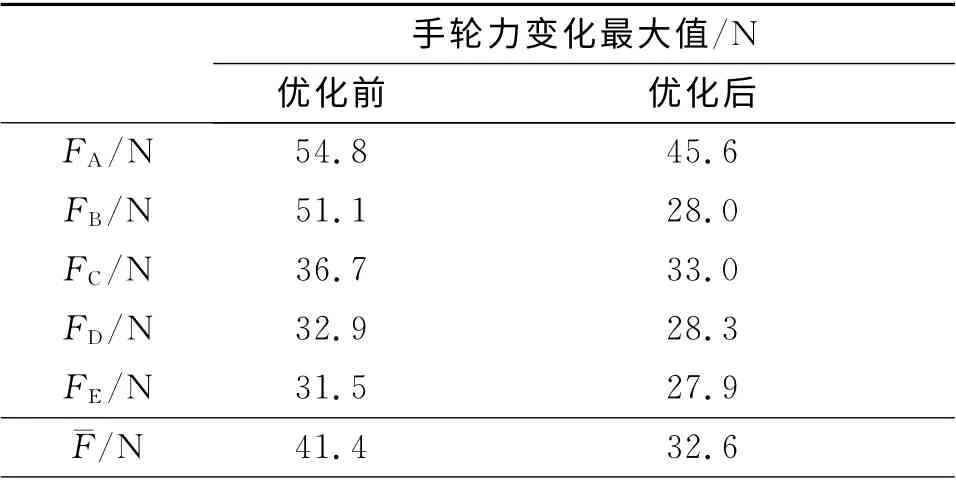
表5 稳健优化前后手轮力变化对比表

由图5看出，A 点在气压相同幅度的变化下，稳健优化后的手轮力值变化幅度减小，稳健性得到了明显提高。因此，本次稳健优化设计是有效的。

5 结论

传统优化方法考虑不到一些不可控因素对产品性能的影响，比如温度、制造误差等。笔者将稳健优化方法引入到高平机参数设计中，将温度作为噪声因子，对高平机进行稳健优化。结果表明，得到的结果相对于确定性优化结果，σ水平由1.347提高到8，显著提高了稳健性，降低了手轮力对温度变化的敏感程度，对提高高平机设计水平和使用性能具有重要的指导意义。

（References）

［1］吴迎春.液体气压式高平机的研究与仿真［D］.南京：南京理工大学，2006.WU Yingchun.Analysis and simulation of hydropneumatic elevating equilibrator［D］.Nanjing：Nanjing University of Science and Technology，2006.（in Chinese）

［2］张训国.螺杆气压式高低平衡机的优化设计研究［D］.南京：南京理工大学，2012.ZHANG Xunguo.Optimization design and research of screw pneumatic elevating equilibrator［D］.Nanjing：Nanjing University of Science and Technology，2012.（in Chinese）

［3］王妍智.火炮高平机系统优化设计及特性分析［D］.南京：南京理工大学，2014.WANG Yanzhi.Optimization design and characteristic analysis of the system of elevating equilibrator［D］.Nanjing：Nanjing University of Science and Technology，2014.（in Chinese）

［4］刘德顺，岳文辉，杜小平.不确定性分析与稳健设计的研究进展［J］.中国机械工程，2006，17（17）：1834－1841.LIU Deshun，YUE Wenhui，DU Xiaoping.Study on uncertainty analysis and robust design：a review［J］.China Mechanical Engineering，2006，17（17）：1834－1841.（in Chinese）

［5］周峰，张学良，贾庭芳，等.稳健设计在单目标优化问题中的仿真应用［J］.太原科技大学学报，2011，32（4）：300－304.ZHOU Feng，ZHANG Xueliang，JIA Tingfang，et al.Simulation and application of robust desigh in singleobjective optimal problems［J］.Journal of Taiyuan University of Science and Technology，2011，32（4）：300－304.（in Chinese）

［6］项立银，顾克秋.基于响应面法炮尾炮闩6σ稳健优化设计［J］.机械制造与研究，2011，40（1）：20－22.XIANG Liyin，GU Keqiu.6σrobust optimal design of breech and block’s fillet based on respond surface method［J］.Machine Building and Automation，2011，40（1）：20－22.（in Chinese）

［7］陈立周.稳健设计［M］.北京：机械工业出版社，1999：13－14.CHEN Lizhou，Robust design［M］.Beijing：China Machine Press，1999：13－14.（in Chinese）

［8］杨冬梅，室津义定.结构稳健性设计与考虑不确定因素的优化设计的比较［J］.力学与实践，2001，23（3）：27－30.YANG Dongmei，MUROTUS YOSHISADA.Comparison between structural robust design and structural optimum design with uncertainties［J］.Mechanics in Engineering，2001，23（3）：27－30.（in Chinese）

［9］杨冬梅.稳健性结构设计的广义有效性［J］.南京理工大学学报，2000，24（6）：506－510.YANG Dongmei.Effectiveness of robust structural design in a broad sense［J］.Journal of Nanjing University of Science and Technology，2000，24（6）：506－510.（in Chinese）

［10］商跃进.轨道车辆零部件稳健性优化设计［J］.内燃机车，2011（8）：19－22.SHANG Yuejin.Robust optimization design of components of railway vehicle［J］.Journal of Internal Combustion Vehicle，2011（8）：19－22.（in Chines）