某大口径杀爆弹杀伤威力计算及优化设计

李 瑞，张明安，张 龙，刘晓蕾，康 狄

（西北机电工程研究所，陕西 咸阳 712099）

在火炮设计过程中，由于射程、机动等性能的要求，不可能无限制地增加装药质量来提高炮弹杀伤威力。对于杀爆弹的设计，要求通过合理选择弹丸结构、壳体材料以及炸药的装药种类等来调整破片数量和质量分布，以达到最优的杀伤威力要求［1］。

在以往的规定中，针对地面有生目标的破片杀伤标准，国外一些国家普遍按照破片动能来划分，破片动能大于78J为杀伤破片，低于78J则认为不具备杀伤能力［2］；在我国的杀伤准则中，常规定质量大于1g的破片为有效破片，质量大于4g的破片为杀伤破片。笔者为计算杀伤面积，规定对人员目标的杀伤概率phk≥0.01为有效破片，杀伤概率按照美国A－S杀伤准则来计算［3］，地面人员取50%卧姿和50%立姿的平均面积，建立杀爆弹自然破片毁伤模型，以某大口径杀爆弹为例，通过装药质量、弹丸壳体质量、壳体厚度以及弹丸着速、落角和炸高等参数，计算得到破片的质量分布和杀伤面积，结合相关试验数据，验证模型的正确性。再以该计算为基础，运用遗传算法理论，以杀伤面积为目标函数，装药质量、弹丸壳体质量、壳体厚度以及弹丸着速、落角和炸高等参数为优化变量，根据杀爆弹的相关设计原则确定约束条件，建立最优化模型进行优化设计。

1 自然破片毁伤模型

爆炸时弹体的破碎与弹体结构、装药种类、弹体材料等有直接关系，但初始裂纹的位置、数量、形状、扩展的方向和速度与弹体材料的不均匀性等随机因素有密切关系［4］，目前还没有准确的理论计算公式来计算破片的数量，相应地，破片的杀伤面积也无法精确计算，笔者采用Gurney方法的半经验公式来建立模型进行计算。建立模型前有两点重要假设：假设炸药化学能全部转化为破片和爆轰产物的动能；气体爆轰产物膨胀过程中密度不变。

计算杀伤面积的数学模型如下：

破片质量呈正态分布，由Mott模型计算：

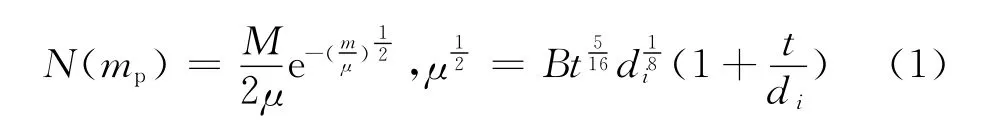
式中：N（mp）为质量大于mp的破片数；M为弹丸壳体总质量；ω为弹丸装药量；2μ为算术平均破片质量；B为由炸药和壳体金属物理特性决定的常数；t为壳体厚度；di为弹丸装药直径。

破片初速按Mott公式［1］计算：

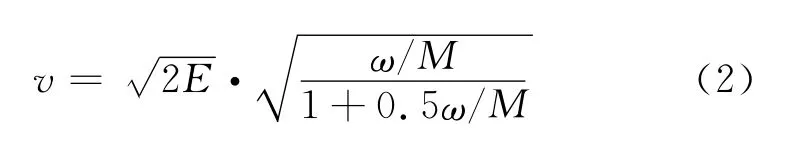
破片飞散密度分布为正态分布，计算飞散后球形密度：

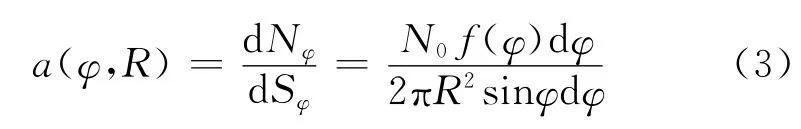
式中：φ为弹轴与飞散方向的夹角，称飞散方位角；R为距爆心相对距离；Nφ为飞散角内破片数；Sφ为球面面积；N0为破片总数；f（φ）为正态分布函数。

计算针对地面战斗人员，按美国A－S 杀伤准则，破片杀伤的条件概率计算公式如下：

式中：v为破片初速；a，b，n为计算不同情况下杀伤概率的常数。

计算杀伤面积：

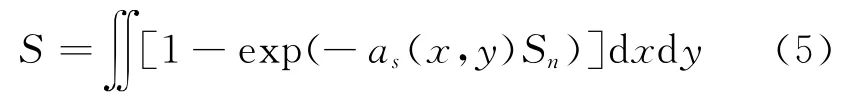
式中：Sn为目标暴露面积；as（x，y）为平均飞散密度。

2 遗传算法优化模型

以对战斗人员的杀伤面积为优化目标，选择装药质量、金属质量、壳体厚度、炸高和落角5个参量为设计变量，根据榴弹设计准则确定约束条件：装药量与壳体质量根据杀爆弹设计经验由其相对质量确定取值范围；弹丸质量还需考虑火炮发射强度的限制、火炮机动性要求、外弹道射程及飞行稳定性等要求，笔者主要针对终点杀伤威力进行优化，故根据前人设计经验确定弹丸质量的约束范围；壳体材料应在满足发射强度的基础上选择高破片率钢，厚度范围为已有弹丸中出现过的设计尺寸；根据弹道理论及实际射击条件给出合理的炸高、落角范围。运用遗传算法进行优化，数学模型如下：

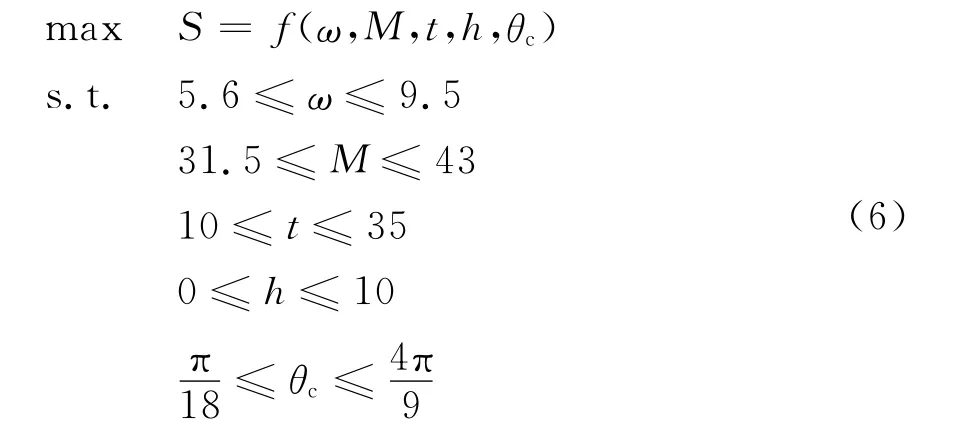
式中：h为炸高；θc为落角。

采用遗传算法，其运算流程［5］如图1所示。

3 计算结果与分析

3.1 正向计算结果

计算以某大口径杀爆弹为例，参照试验数据［6］，取装药质量8.5kg，弹体金属质量37.4kg，壳体平均厚度13mm，弹丸气动外形特征参数：弹长5.82d，头部长3.26d，圆柱部长1.9d，尾椎长0.655d，船尾角设6°，其中d为弹丸直径。计算静态杀伤威力，假设战斗部中心起爆，炸高3 m，落角0.82rad，计算结果如图2～3所示。

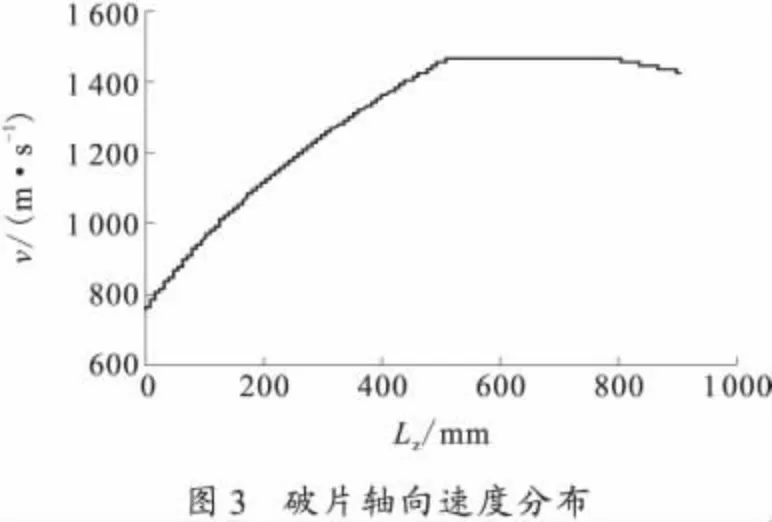
由图2可得：质量大于1g的破片数 为4 158；质量大于4g的破片数 为2 162，破片总数为7 996，破片平均质量4.7g，破片初速计算为1 047m／s。图3反映了距弹丸头部不同距离Lz处对应的破片初速分布，假设金属壳体碎为均匀破片，圆柱部产生的破片初速最大，而头部和尾部的破片初速较小。

仿真计算结果与试验数据对比情况如表1所示。

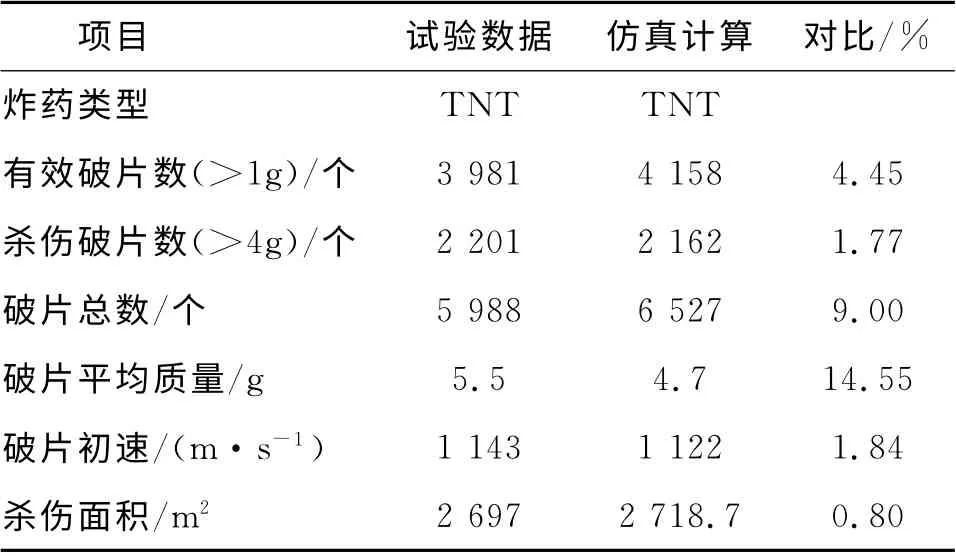
表1 仿真计算结果与试验数据比较

由表1可知，仿真计算结果与试验数据符合较好，计算得到的有效破片数、杀伤破片数及杀伤面积等重要指标与试验数据相差不超过5%，验证了算法的可行性和模型的正确性。

3.2 优化结果

分别取遗传代数为100、300、500、800 进行计算，采用各代中最优个体的适应度值和群体的平均适应度值作为遗传算法的评估指标。图4～7为优化结果及性能跟踪。

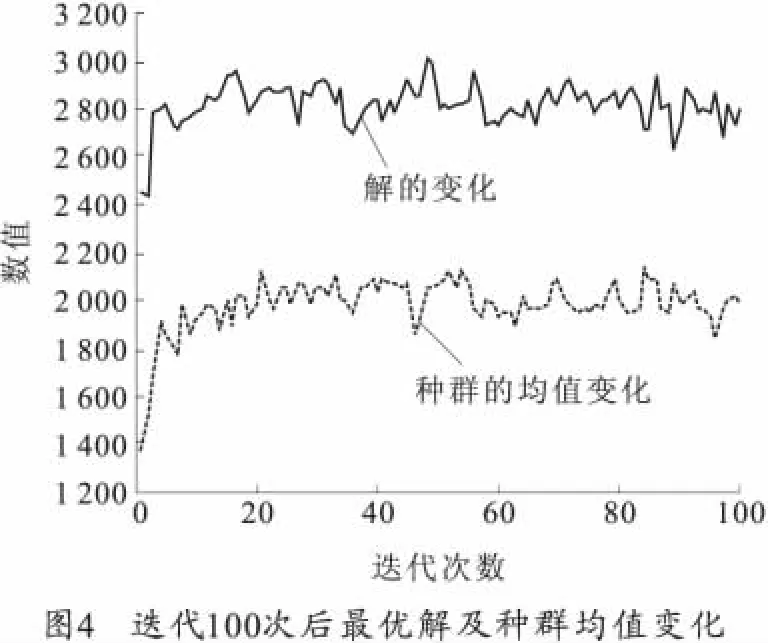
给出杀伤面积最大值对应的优化参数的值，并与定型方案参数比较，结果如表2所示。

表2 不同迭代次数的优化结果

通过优化结果，可以得到以下结论：

1）迭代800 次后，得到最大杀伤面积值为3 038，比定型方案2 697提高约12.6%。

2）在取值范围内，装药量与金属质量值越大，杀伤面积越大，符合试验规律。

3）以战斗人员为杀伤目标，有利的杀伤面积优化结果对应的壳体厚度相对小，因此设计中金属强度在满足弹丸安全发射条件时，壳体越薄，对地面人员的杀伤面积越大。

4）不同的迭代次数后得到的炸高和落角的最优解趋于一致，最佳炸高为2.5～3m，最佳落角为0.83～0.84rad，即48°左右，该数据对战斗部引信设计和外弹道设计具有参考价值。

4 结束语

根据国内外常用的经典终点弹道经验公式，建立了终点毁伤模型，并以该模型为基础进行了数值模拟计算，模拟计算结果与实际试验数据一致性较好，从而验证了该模型的正确性和算法的可行性。与此同时，笔者以所建立的终点毁伤模型为基础，以对战斗人员的杀伤面积为优化目标，建立了应用遗传算法的最优化模型，对装药结构、壳体厚度和起爆条件等重要参数进行了优化，优化变量的约束条件根据弹丸的相应设计准则确定，优化结果显示杀伤面积比原参考数据提高12.6%，而相应的优化参量数值也符合各参数对杀伤威力的影响规律［6］，结果验证了遗传算法应用于终点毁伤设计的可行性和正确性，对武器系统全弹道设计具有参考价值。

（References）

［1］CARLUCCI D E，JACOBSON S S.Ballistics：theory and design of guns and ammunition［M］.New York：CRC Press of Taylor ＆Francis Group，2007：152.

［2］王儒策，赵国志.弹丸终点效应［M］.北京：北京理工大学出版社，1993：78.WANG Ruce，ZHAO Guozhi.Terminal ballistics effects of projectile［M］.Beijing：Beijing Institute of Technology Press，1993：78.（in Chinese）

［3］魏惠之，朱鹤松，汪东晖，等.弹丸设计理论［M］.南京：南京理工大学出版社，2009：261.WEI Huizhi，ZHU Hesong，WANG Donghui，et al.Theory and design of projectile［M］.Nanjing：Nanjing University of Science and Technology Press，2009：261.（in Chinese）

［4］王凤英，刘天生.毁伤理论与技术［M］.北京：北京理工大学出版社，2009：75.WANG Fengying，LIU Tiansheng.Damage theory and technology［M］.Beijing：Beijing Institute of Technology Press，2009：75.（in Chinese）

［5］雷英杰，张善文.遗传算法工具箱及应用［M］.西安：西安电子科技大学出版社，2013：43.LEI Yingjie，ZHANG Shanwen.Matlab genetic algorithm toolbox and its application［M］.Xi’an：Xidian University Press，2013：43.（in Chinese）

［6］刘晋，陈国光，纪彩华，等.不同落角与炸高对弹丸杀伤面积的影响［J］.机械管理开发，2010，25（3）：21－22.LIU Jin，CHEN Guoguang，JI Caihua，et al.The different off angle and deep－fried high’s Impact on the anti area of the projectile［J］.Mechanical Electronic Engineering Institute，2010，25（3）：21－22.（in Chinese）