基于样条插值的不完备信息系统参数估计

李 珍,魏利胜∗,程运昌(.安徽工程大学电气工程学院,安徽芜湖,4000; .国网霍邱县供电有限责任公司,安徽六安,37400)

基于样条插值的不完备信息系统参数估计

李 珍1,魏利胜1∗,程运昌2
(1.安徽工程大学电气工程学院,安徽芜湖,241000; 2.国网霍邱县供电有限责任公司,安徽六安,237400)

研究一种不完备信息系统参数辨识插补法.首先将每个输入信号加上时间戳,即将输入信号进行时间顺序排序,使数据在特定的时刻缺失;并采用样条插补法,自适应补充缺失数据,即当缺失一个输出数据时,应用线性样条插值法填补缺失数据,当连续缺失两个或两个以上的数据时,应用三次样条插值法进行补充;在此基础上应用粒子群算法对插补后的不完备信息系统进行参数精确估计;最后,通过MATLAB仿真实验验证了该方法在不同缺失率下,其参数估计的精确性与有效性.

不完备信息;样条插值;粒子群算法;参数估计

系统辨识已广泛应用于各行各业[1].系统的参数估计是根据已知的输入信号与输出数据来估计此系统中控制器的参数值.在此过程中,往往会因为仪器或人为因素导致某些数据的丢失.如果直接使用存在丢失的数据来估计参数,结果显然会存在偏差[2].因此,必须采取一种方法如插补法将缺失的数据补充完整,再进行参数的估计[3].目前,由于数据缺失使得很多系统研究都不能更顺利地进行,因此插补法已成为广大研究者们关注的焦点.加权估计法、似然插补法以及多重插补法等被广泛运用[4];Cheti Nicoletti[5]对不同插补方法进行了比较;Hai Zhong[6]对多重插补法又做了新的探讨;林东方[7]对期望最大化算法进行了探讨;R Pintelon[8]等将缺失的数据当作未知的参数;而谭彦华[9]将样条插值法应用到模糊系统中.

对于插补法的研究已取得了一定的成绩,但是,当缺失多个数据时,回归插补法效果不好;缺失单个数据时,多重插补法的效果不好;缺失率大的时候,似然插补法效果不好.加权插补法需要假设同一调整组内的单元具有相等的回答概率[2].而当缺失单一的数据时,采取线性的样条插补法.当缺失两个或两个以上的数据时,就应用三次样条插值法.样条插值可以在缺失率相对较大时仍具有良好的插补效果,且不需要添加辨识的参数.而粒子群算法的程序较简单,需要修改的参数很少.因此,采用样条插值法与粒子群算法的结合来实现对不完备信息系统参数的较精确估计.

1 样条插值法基本原理

根据完备信息系统参数估计的原理框图来画出不完备信息系统参数估计的原理框图如图1所示.在已知系统输入信号u(t)与噪声信号v(t)的前提下,应用样条插补法将存在数据缺失的输出补充完整,得到输出值z(t).将插补后的系统输出值z(t)与选择的数学模型输出值^Z(t)之间的误差e(t)返回到粒子群算法,粒子群算法辨识出一组参数,将该组参数带入数学模型,重新产生一个数学模型输出值^Z(t).重复取两者之间的误差,直到达到事先规定的迭代次数或者误差e(t)在事先规定的精度范围内时,停止运算,此时对应的参数组就是该算法辨识的参数大小.

1.1 样条插值法基本原理

根据已知的数据对,寻求一组较好的拟合多项式[10].运用该多项式来拟合每对相邻数据点之间的函数曲线,然后求出缺失值[3].将区间[a,b]划分成n等份,即a＝t1＜…＜tn＝b,称为Ω.函数z(t)需要满足:

线性样条插值法:

当z(t)在每对[ti,ti＋1](i＝1,2,…,n－1)上的多项式次数不超过1次,并且满足1个以上的子区间函数最高次数为1次,则称z(t)是关于Ω的线性样条函数.线性样条函数的表达式如下:

三次样条插值法:

当z(t)在每对区间[ti,ti＋1](i＝1,2,…,n－1)上都是次数不超过3次的多项式,并且最少在1个子区间上函数最高次数为3次,就称z(t)是关于Ω划分的三次样条函数.令经过已知n个样本数据点(ti, Yi)(i＝1,2,…,n),t1＜t2＜…＜tn的三次样条函数为z(t)[9].令:其中,未知系数ai,bi,ci,di需要满足条件:z(ti)＝Yi,z(ti－0)＝z(ti＋0)和z′(ti－0)＝z′(ti＋0),z″(ti－0)＝z″(ti＋0).此处添加的是第2类边界条件即z″(a)＝Y″(a),z″(b)＝Y″(b).又令z″(ti)＝Ni,z″(ti＋1)＝Ni＋1,令hi＝ti＋1－ti[8].将z″(t)进行两次积分得到如下的表达式:

根据z(ti)＝Yi,z(ti＋1)＝Yi＋1,可得:

保持z(t)在节点处的连续性,即z′(ti－0)＝z′(ti＋0)和z′i(ti－0)＝z′i＋1(ti＋0).令再把第一边界条件z′(t1)＝Y′1,z′(tn)＝Y′n带入z′(t)得出下列的方程组:

1.2 粒子群优化算法基本原理

设实函数F是定义在欧式空间ED的某一区域S上的.空间维数为D,粒子个数为L,那么第i个粒子在该区域S中的位置、速度以及该时刻的适应度分别表示为:X 0i＝(X 0i1,X 0i2,…,X 0iD)T∈S,Vi＝(Vi1,Vi2,…,ViD)和Fitnessi＝F(X 0i),其中i＝1,2,…,L.第i个粒子寻求到曾经的最佳位置和对应的最佳适应度分别是:Y 0i和p(i)[1].第i个粒子搜索到的全部粒子中的最优位置和对应的最佳适应度分别表示为:pg和fitness(D,pg).引入惯性权重w的粒子群算法的步骤如文献[1]中所示.

其中d＝1,2,…,D,每个粒子的位置与速度按下式变化如下:

收敛性证明:

其中w∈(0,1)的随机数,同时c1,c2∈(0,2)的随机数.Vi、X 0i是相互独立的,因此可以对其一维进行分析.由于每一个粒子的自身历史最优位置Y 0与全部粒子中的最优位置pg是保持不变的[11],因此可以将Y 0、pg、w、c1及c2当作常数.化简式(8)、式(9)得:

又

将式(10)、式(11)带入式(12)得出:

运用特征方程法来求解式(13)c.＝c1＋c2,此一元二次方程的求解有3种情况:当Δ＝0时,λ＝λ1＝λ2＝此时X 0(i)＝(A0＋A1∗i)∗λi,其中A0,A1为待定的系数;当Δ＞0时,λ1,2＝此时X 0(i)＝A0＋A1∗λi1＋A2∗λi2;其中待定系数为A0,A1,A2;若Δ＜0时,那么X 0(i)＝A0＋A1∗λi1＋A2∗λi2,其中待定系数为A0,A1,A2.

2 基于样条插值的不完备信息的参数辨识

对于不完备信息的一类单输入单输出线性系统[13]基本结构图如图2所示.由图2可知,系统的输入信号、噪声信号分别为u1(k)、v1(k).v1(k)是均值为零,方差为σ2的高斯白噪声.系统的传递函数用G(z－1)来表示,输出用Z(k)来表示.存在数据缺失的输出是Z0(k).u1(k)与Z0(k)是可以观测的.z(k)是采用插补法插补后的系统输出.一般情况下有下列表达式:

当满足如式(17)关系时,该系统是滑动模型.

已知参数的阶次na,nb和nd,令:

化简式(17),得到该系统的最小二乘格式:

运用粒子群算法将辨识的问题转化成优化问题来思考.由式(14)可表示出系统的偏差准则函数:

粒子群算法是从进化的方面来考虑问题的,Pbest(θ)是该算法的适应度函数.由于式(20)是在线的优化问题,因此运用PSO(Particle Swarm Optimization,粒子群优化)算法探求满足适应度函数值最优(即值最小)的参数,这些参数就是需要估计的参数大小.

3 仿真实验

仿真实验采取MATLAB软件来完成.首先在完整数据的条件下,采用最小二乘遗传递推算法、PSO算法产生输入信号、噪声信号、输出信号、初始随机位置矩阵和对应的速度矩阵以及一些辅助信号,在不同缺失率下产生不同的输出,结合保存下来的数据,分别采用样条插值粒子群算法和无插值最小二乘遗传递推算法来实现该类系统的参数辨识[13].

对于该系统的样条插补粒子群优化算法和无插补最小二乘遗传递推算法的仿真结果如式(21)所示:

式中,v(k)是零均值的白噪声,输入u(k)采用6阶M序列,幅度为1,数据个数L＝100,D＝5,加权阵取单位阵.给定初始条件:beita＝0.999,miu＝beita^2,P 0＝10^6∗eye(D),theta 0＝10^(－3)∗ones(D,1), P(1:D,1:D,1)＝P 0,theta(1:D,1)＝theta 0,A(k)＝1.学习的因子:c1＝1.496 2,c2＝1.496 2,其惯性权重w＝0.729 8,最大循环次数Max DT＝100,待估计参数个数为D.满足w＜1,c＞0与2∗w－c＋2＞0,所以算法收敛.最后比较两种插补方法插补后系统的参数估计、性能函数.以下给出仿真的所有数据与图形,为样条插值法在系统辨识领域的应用打下基础.

模型产生的随机输入信号、噪声信号如图3所示,图3中噪声信号的不同线条个数代表了不同的维数,噪声信号是一个L×L维的信号.

不同缺失率下不同插补辨识法的参数估计值如表1所示.由表1可知,在相同的数据缺失率下,采取样条插值粒子群算法使不完备系统的参数估计较准确、收敛速度较快、稳定性也较强.5%缺失率时,参数及性能函数的变化情况如图4所示.10%缺失率时,参数及性能函数的变化情况如图5所示.20%缺失率时,参数及性能函数的变化情况如图6所示.30%缺失率时,参数及性能函数的变化情况如图7所示.在图4～图7中,a1表示参数a1的真实值;a11表示参数a1在各缺失率下采用样条插值粒子群算法进行辨识的估计值;a12表示参数a1在各缺失率下采用文献[14]方法即无插值最小二乘遗传递推算法进行辨识的估计值;Pbest表示该系统在各缺失率下采用样条插值粒子群算法进行辨识的性能函数;J表示该系统在各缺失率下采用无插值最小二乘遗传递推算法进行辨识的性能函数.图4中其他参数的表示同a1的各种表示意义是一样的.

在相同缺失率下,采用样条插值粒子群算法估计的参数值更接近真实值,且其收敛的速度也更快.由表1可知,在缺失率为5%时,对于参数a1,采用样条插值粒子群算法估计值a11为－1.499 3,而采用无插值最小二乘遗传递推算法的估计值a12为－1.107 1;对于参数a2,采用样条插值粒子群算法估计值a21为0.698 4,而采用无插值最小二乘遗传递推算法的估计值a22为0.366 1;对于参数b1,采用样条插值粒子群算法估计值b11为0.982 4,而采用无插值最小二乘遗传递推算法的估计值b12为1.106 0;对于参数b2,采用样条插值粒子群算法估计值b21为0.495 8,而采用无插值最小二乘遗传递推算法的估计值b22为0.397 7;对于参数d1,采用样条插值粒子群算法估计值d11为0.932 7,而采用无插值最小二乘遗传递推算法的估计值d12为0.004 5.从数字可以直观看出,样条插值粒子群算法的估计值更准确.表格中的其他缺失率下的数据同样可以得出此结论.

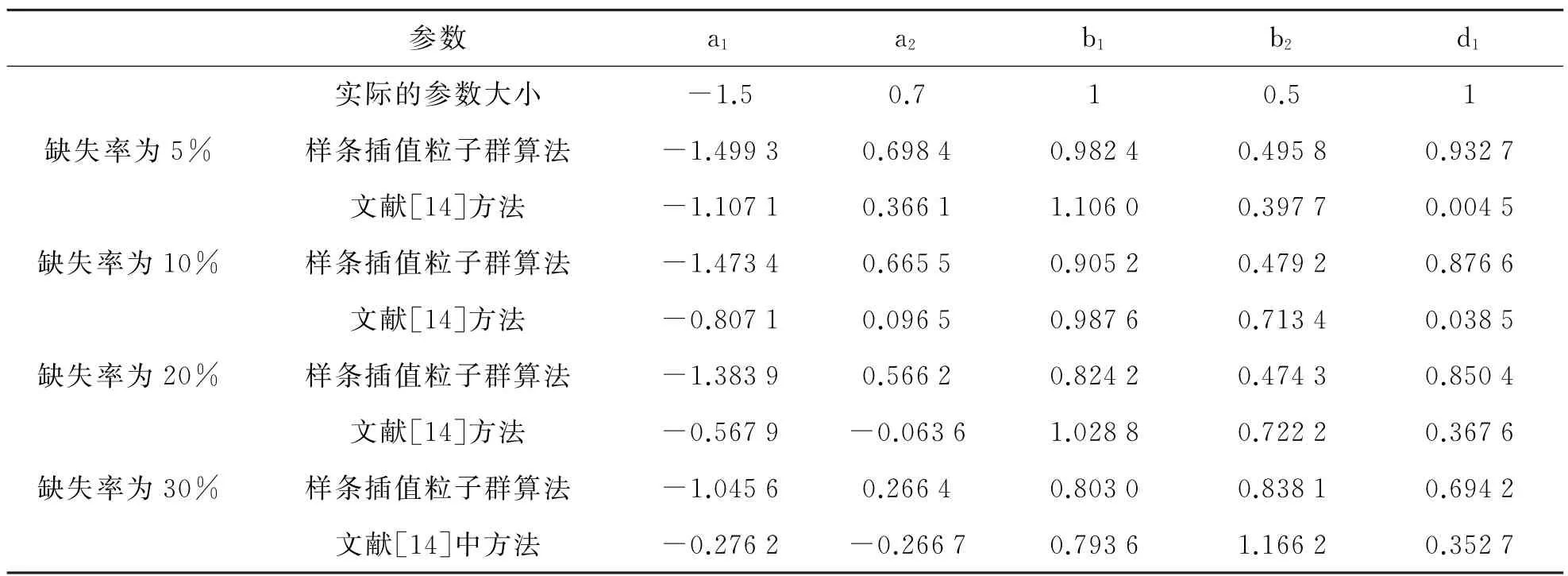
表1 不同缺失率下不同插补辨识法的参数估计值(迭代100次)

在相同缺失率下,由图5可知,在缺失率为10%时,对于参数a1采用样条插值粒子群算法估计值a11,在进化次数达到40次左右的时候就开始趋向收敛,且波动比较平缓,最终收敛于－1.473 4;而采用无插值最小二乘遗传递推算法的估计值a12,在进化次数达到60次左右的时候才开始趋向收敛,且波动不够平缓,最终收敛于－0.807 1.在缺失率为10%时,对于参数a2采用样条插值粒子群算法估计值a21,在进化次数达到30次左右的时候就开始趋向收敛,且波动比较平缓,最终收敛于0.665 5;而采用无插值最小二乘遗传递推算法的估计值a22,在进化次数达到40次左右的时候才开始趋向收敛,且波动不够平缓,最终收敛于0.096 5.在缺失率为10%时,对于参数b1采用样条插值粒子群算法估计值b11,在进化次数达到35次左右的时候就开始趋向收敛,且波动比较平缓,最终收敛于0.905 2;而采用无插值最小二乘遗传递推算法的估计值b12,在进化次数达到70次左右的时候才开始趋向收敛,且波动不够平缓,最终收敛于0.987 6.在缺失率为10%时,对于参数b2采用样条插值粒子群算法估计值b21,在进化次数达到35次左右的时候就开始趋向收敛,且波动比较平缓,最终收敛于0.479 2;而采用无插值最小二乘遗传递推算法的估计值b22在进化次数达到60次左右的时候才开始趋向收敛,且波动不够平缓,最终收敛于0.713 4.在缺失率为10%时,对于参数d1采用样条插值粒子群算法估计值d11,在进化次数达到35次左右的时候就开始趋向收敛,且波动比较平缓,最终收敛于0.876 6;而采用无插值最小二乘遗传递推算法的估计值d12,在进化次数达到60次左右的时候才开始趋向收敛,且波动不够平缓,最终收敛于0.038 5.

从表1和参数仿真图都可以看出,随着缺失率的增大,辨识的效果越来越差.由表1可知,同样采用样条插值粒子群算法进行参数估计,对于参数a1,在缺失率为5%时,估计的值a11为－1.499 3;在缺失率为10%时,估计的值a11为－1.473 4;在缺失率为20%时,估计的值a11为－1.383 9;在缺失率为30%时,估计的值a11为－1.045 6.从数字的变化可以证明该结论.同样的,由图4b、图5b、图6b和图7b可以看出,同样采用样条插值粒子群算法进行参数估计,对于参数b1,在缺失率为5%时,进化次数达到28次左右就开始趋向收敛,波动很平缓;在缺失率为10%时,进化次数达到35次左右开始趋向收敛,波动平缓;在缺失率为20%时,进化次数达到40次左右开始趋向收敛,波动相对较平缓;在缺失率为30%时,进化次数达到50次左右开始趋向收敛,波动不够平缓.

在相同的缺失率下,采用样条插值粒子群算法的系统性能函数收敛速度快得多.由图4f、图5f、图6f和图7f可知,在缺失率为5%时,采用样条插值法粒子群算法的系统性能指标Pbest只需要20次左右就开始趋于收敛,性能函数的最大值只有110,收敛于6.420 2;采用无插值最小二乘遗传递推算法的系统性能指标J需要60次左右才开始趋于收敛,性能函数的最大值接近3 400,收敛于2.291 671 2e＋002.但是随着缺失率的增大,不管是样条插值粒子群算法还是无插补最小二乘遗传递推算法,插补后系统的性能指标的收敛速度都渐渐降低,性能指标的最大值都越来越大,同时最终收敛的值也随之变大.如采用样条插值粒子群算法的系统,在缺失率为10%时,系统的性能指标Pbest的最大值只有130,收敛于26.687 9;在缺失率为20%时,系统的性能指标J的最大值达到190,收敛于66.544 3.

4 结论

通过仿真图及仿真数据可以直观地看出,对于不完备信息系统,在相同的数据缺失率下,样条插值法可以实现较好的插补效果.在缺失率达到较高的数值时,样条插值法依然能够实现有价值的插补作用,从而使得该系统的参数得以较准确地估计.但是在缺失率增加到一定值时,由辨识参数的图形和大小以及系统的性能函数可知,该插补法已无法较精确地模拟完整数据的系统.文章主要讨论的是不同缺失率下样条插值粒子群算法对系统参数的估计问题.样条插值法是一种应用较为广泛的插补法,但将其运用在需要辨识参数的系统中还较少.为了进一步探讨样条插值法的适用价值,可以在缺失率更高时采取其他的辨识方法,来实现更精确的参数估计.

[1] 刘党辉,蔡远文,苏永芝,等.系统辨识方法及应用[M].北京:国防工业出版社,2010.

[2] 金勇进,邵军.缺失数据的统计处理[M].北京:中国统计出版社,2009.

[3] 陈浩,华灯鑫,张毅坤,等.基于三次样条函数的激光雷达数据可视化插值法[J].仪器仪表学报,2013,34(4):831-837.

[4] R J A Little,D B Rubin.Statistical analysis with missing data[M].U.S.A:Wiley&Sons,2002.

[5] U Nur,N T Longford,J E Cade,et al.The impact of handling missing data on alcohol consumption estimates in the UK wemon cohort study[J].Eur J Epidemiol,2009,24(1):589-595.

[6] H Zhong.The impact of missing data in the estimation of concentration index:a potential source of bias[J].Eur J Heslth Econ,2010,11(1):255-266.

[7] 林东方,宋迎春,金昊.不完全测量数据的EM处理算法[J].大地测量与地球动力学,2011,31(4):112-115.

[8] R Pintelon,J Schoukens.Identification of continuous-time systems with missing data[J].Instrumentation and Measurement,IEEE Transactions on,1999,48(3):736-740.

[9] 谭彦华,李洪兴,马秀娟,等.B样条函数在模糊系统中的应用[J].控制理论与应用,2013,30(11):1 445-1 456.

[10]张晓丹,邵帅,刘钦圣.基于样条函数的光滑支持向量机模型[J].北京科技大学学报,2012,34(6):718-725.

[11]高尚,汤可宗,蒋新姿.粒子群优化算法收敛性分析[J].科学技术与工程,2006,6(12):1 625-1 627.

[12]杜大军,商立立,漆波,等.一种不完全信息下递推辨识方法及收敛性分析[J].自动化学报,2015,41(8):1 502-1 515.

[13]侯媛彬,汪梅,王立琦.系统辨识及其MATLAB仿真[M].北京:科学出版社,2004.

[14]S Rhode,F Gauterin.Online estimation of vehicle driving resistance parameters with recursive least squares and recursive total least squares[J].Intelligent Vehicles Symposium(IV),2013 IEEE,2013,10(1109):269-276.

Parameter estimation for the incomplete information system based on spline interpolation

LI Zhen1,WEI Li-sheng1∗,CHENG Yun-chang2
(1.College of Electrical Engineering,Anhui Polytechnic University,Wuhu 241000,China; 2.State Grid Huoqi County Electric Power Supply Company,Luan 237400,China)

In this issue,a recognition and interpolation method of parameter in an incomplete information system was discussed.Firstly,made the data lost on a certain time by sorting the input signals in the order of time after adding timestamp on each of them.The missing message was supplemented adaptively using spline interpolating,which means the data was supplemented adaptively using linear spline interpolating when one output signal was lost,using the cubic interpolating when two or more output signals were lost.Based on these,the parameter was precisely estimated by particle swarm optimization in the interpolation system.Finally,the precision and effectiveness of the parameter estimation in different missing rates was verified by the method of MATLAB simulation experiment.

incomplete information;spline interpolating;particle swarm optimization;parameter estimation

TP273

A

1672-2477(2015)05-0069-09

2015-09-24

国家自然科学基金资助项目(61203033、61172131、61271377)

李 珍(1989-),女,安徽枞阳人,硕士研究生.

魏利胜(1978-),男,安徽巢湖人,副教授,博士.