基于弹塑性本构的单股钢丝绳受力分析
2015-11-19任志乾于宗乐陈循王岩磊
任志乾,于宗乐,陈循,王岩磊
(1.国防科学技术大学装备综合保障技术重点实验室,湖南长沙410073;2.92537部队,北京100161)
基于弹塑性本构的单股钢丝绳受力分析
任志乾1,于宗乐1,陈循1,王岩磊2
(1.国防科学技术大学装备综合保障技术重点实验室,湖南长沙410073;2.92537部队,北京100161)
针对单股钢丝绳在受到冲击载荷作用下的失效问题,采用有限元法开展了其结构弹塑性分析。利用钢丝绳单丝试验数据,拟合得到了相应的弹塑性本构模型参数,根据钢丝绳钢丝几何空间构型,建立了钢丝绳的三维有限元模型。在静载荷和冲击载荷下分别对钢丝绳内部钢丝的受力进行了计算,得到了在各层钢丝的Von Mises应力和等效塑性应变分布。结果表明,各层钢丝内侧接触部位的Von Mises应力和等效塑性应变均相对较大,是引发钢丝绳结构失效的关键部位。
固体力学;单股钢丝绳;冲击载荷;弹塑性分析
0 引言
钢丝绳是一种用于承受拉伸载荷的常见功能结构单元,由于其具有柔性空间螺旋结构特点,在工程中发挥着重要的作用,被广泛应用于矿山、桥梁、船舶、航空、航天等领域。由于钢丝绳重要性,其结构安全性和可靠性一直是工程人员关注的热点问题。
研究钢丝绳的安全性和可靠性,首先要清楚钢丝绳在不同载荷下的失效机理,因此国内外学者对钢丝绳在受到外载作用下其内部结构的应力应变分布规律开展了大量的研究工作。Costello等[1]对钢丝绳的结构、整绳的受力分析和钢丝绳的摩擦特性进行了分析。velinsky等[2]提出了解决复杂钢丝绳模型的非线性理论,并应用于不同绳芯的钢丝绳中。Ghorei等[3]基于经典Kirchhoff曲杆弹性理论建立了钢丝绳平衡方程,推导了载荷与变形间的关系。沈燕等[4]利用试验的方法研究了不同接触载荷下钢丝的微动磨损行为。Beretta等[5]研究了钢丝的疲劳强度与表面质量的关系。王世文等[6]对钢丝绳的各类模型和研究方法进行了对比分析。
但是由于受载条件下的钢丝绳结构以及各钢丝之间相互接触、摩擦与挤压作用的过程极其复杂,采用单一的理论或试验方法均难以给出钢丝绳之间的复杂相互作用的状态以及应力应变变化规律。
随着计算技术的发展,采用数值方法对钢丝绳分析成为重要的研究手段,尤其是有限元法以及计算机辅助设计CAD和计算机辅助工程CAE软件的发展,使得模拟钢丝绳这类复杂结构的力学响应变得十分方便。Nawrocki等[7]建立了单股钢丝绳的有限元模型。马军等[8]针对6×7IWS钢丝绳的构型及受载特点,应用微分几何理论建立了三维几何模型,并基于ANSYS软件采用弹性本构模型对其进行了应力应变分析。张德坤等[9]以6×19点接触式提升钢丝绳为研究对象,通过试验与仿真对比研究了钢丝绳内钢丝之间接触载荷与钢丝磨损之间的关系。上述对于钢丝绳分析多是考虑钢丝绳受到静力载荷或是远小于破断力的动载荷下的受力情况,因此在分析过程中仅将钢丝绳作为弹性材料,采用弹性材料本构进行分析。而钢丝绳在实际工作过程中由于各种原因可能会受到冲击载荷的作用。尤其是一些特殊用途的钢丝绳,如用于航空阻拦,起重吊运等钢丝绳在瞬间受到的冲击载荷量级往往能够达到钢丝绳额定破断载荷的50%~60%,在这种冲击载荷作用下,可能会导致内部钢丝的局部塑性变形,对于钢丝绳的安全性与可靠性会造成很大的影响。本文采用高应变率弹塑性本构模型,对钢丝绳在受到冲击载荷作用下,钢丝绳在瞬时大张力作用下内部钢丝之间应力应变进行分析。首先利用试验方法拟合确定本构模型参数,以某型单股钢丝绳为例,利用Pro/E软件建立其三维几何模型,并采用Abaqus有限元软件,建立考虑接触效应的有限元模型,进而根据钢丝绳在工作过程中的载荷条件,开展相应的有限元分析,分析拉伸载荷与轴向相对伸长率之间的关系,并与试验数据进行对比校核,并先后开展拉伸静态与冲击载荷作用分析,给出内部各层钢丝之间的应力应变分布规律,为开展钢丝绳在冲击载荷作用下的失效分析提供基础。
1 钢丝弹塑性本构方程及其数值模型
1.1 钢丝的弹塑性本构方程
钢丝绳在工作过程中受到的冲击载荷往往能够达到钢丝绳额定破断载荷的50%~60%,在这种载荷条件下,钢丝绳内部钢丝局部可能已发生了不可逆的塑性变形,此外冲击载荷下的应变率往往较高。因此,需要采用高应变率下的弹塑性本构对钢丝绳在冲击载荷作用下的受力情况进行分析。为此,本文采用如下Ramberg-Osgood本构关系:

式中:σ为应力;ε为应变;σ0为材料屈服强度;ε0为材料屈服应变;α、n为材料常数。
(1)式属于材料在单轴下的拉伸过程,在材料均匀性和力学性能各向同性假设的基础上,易将(1)式进一步推广到三维情况。在小应变弹塑性情况下,可将应变率张量分解为弹性部分e和塑性部分p:


式中:C为材料弹性张量。
适用于金属塑性的J2流动模型中,其屈服条件为
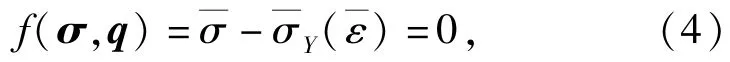
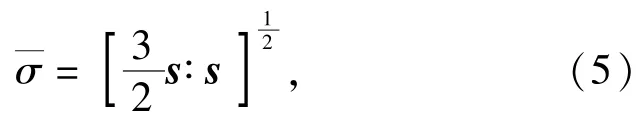
其中s为Cauchy应力偏张量。
此外,塑性流动法则和内变量的演化方程为
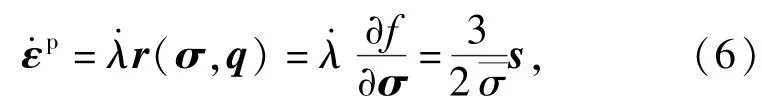

式中:D为变形率张量;h为材料强化模量。
1.2 应力更新算法
对于材料非线性问题的计算,常采用增量有限元法进行求解,需将本构方程在时域中进行离散,进而实现应力更新。本文的弹塑性本构模型的应力更新采用径向返回算法,并采用Newton-Raphson迭代法对非线性方程进行求解,最终实现当前时刻应力的更新,其具体流程如下:
1)给定应力初始值σ(0)、应变初始值εp(0)和标量塑性流动率Δλ(0)为

2)在第k次迭代时,检查屈服条件:

如果f(k)<0,则认为收敛,本增量步的迭代结束并返回相应参数数值,否则转至流程3. 3)计算塑性参数增量

4)更新等效塑性应变、内变量以及应力
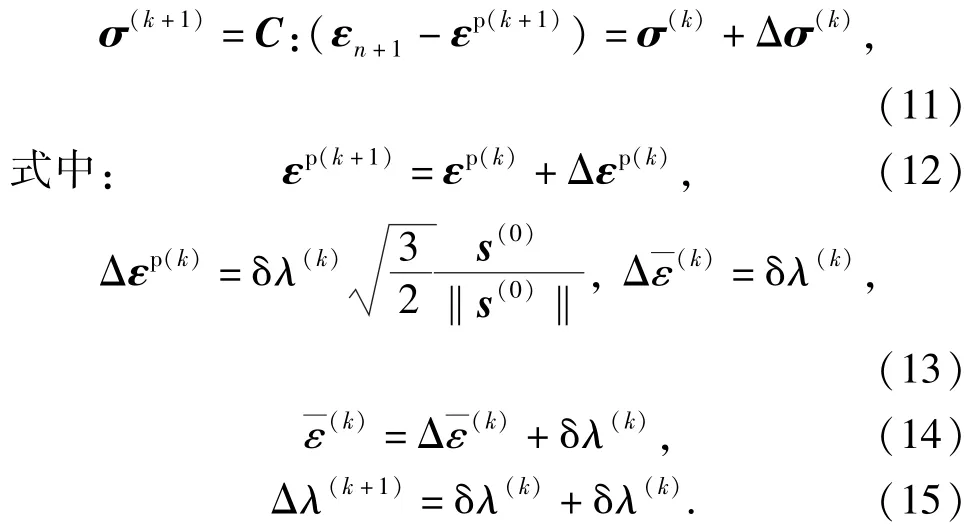
然后将更新的变量返回屈服条件进行检查,整个迭代过程将重复直至收敛或者超出迭代次数上限为止。基于上述数值分析过程,结合Abaqus仿真软件的UMAT材料子程序接口编程,可实现该弹塑性本构模型在实际结构有限元分析中的应用。
2 钢丝力学性能试验及其本构方程确定
通过对某型单股钢丝绳的两种不同直径钢丝开展的力学性能试验分析,利用单轴拉伸试验,测量得到各个钢丝的载荷-应变之间的变化关系曲线,并利用试验数据对上述的弹塑性本构模型参数进行拟合,进而确定钢丝的弹塑性本构模型。
根据钢丝绳中直径分别为d=2.6 mm和d= 3.1 mm的两种钢丝的单轴拉伸试验结果,得到应力应变的试验曲线,如图1.再根据两种直径钢丝的拉伸试验数据,分别对上述Ramberg本构模型参数进行拟合,首先对本构方程两边取自然对数,再根据试验得到材料应力应变曲线,采用线性最小二乘法拟合得到本构方程的参数,得到了两种钢丝的屈服强度σ0、弹性模量E、屈服应变ε0,α以及n等本构模型参数结果,列于表1中。

图1 两种直径钢丝的单轴应力应变试验曲线Fig.1 The uniaxial stress-strain curves for two wires

表1 两种钢丝本构模型参数的拟合结果Tab.1 Fitted test results of the wire constitutive model parameters
3 钢丝绳的有限元模型及算例分析
3.1 钢丝绳的有限元模型
以某单股钢丝绳为研究对象,采用上述弹塑性本构对其开展仿真分析。首先应用微分几何理论建立钢丝绳几何模型[10],其中绳芯丝空间曲线方程为

式中:s为选取股芯线长度;t为均匀刻度分布系数。
钢丝绳侧线钢丝曲线方程为
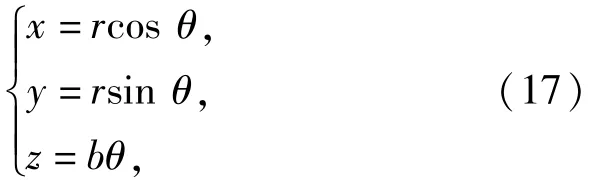
式中:r为绳芯绳股中绕股芯钢丝做捻转的侧线钢丝螺旋半径;θ为侧股在绳芯绳股中的螺旋角;,ρ为螺旋线螺距。
本文选取的单股钢丝绳为1×19结构,基于CAD软件Pro/E建立丝-绳数字化的三维几何模型。其特征参数为:单股钢丝绳直径D=12 mm,股内芯丝直径d=3.1 mm,外侧由两层分别为6根和12根直径d=2.6 mm绕中心丝作同心捻转的侧线钢丝构成,股内钢丝捻距54 mm.根据结构的对称性特点,取轴向长度为22 mm的结构,建立如图2所示的几何模型。采用Abaqus软件对上述几何模型划分有限元网格,建立如图3所示的有限元网格模型,共包含51 300个六面体网格,63 802个节点。
在钢丝绳承载过程中,各钢丝之间存在挤压接触与滑移摩擦等现象,钢丝之间的接触对钢丝绳整体性能、局部应力场具有重要影响,因此不能轻易忽略。接触问题属于高度非线性问题,接触物体不可相互侵入,接触力的法相分量只能是压力而不能是拉力,在考虑摩擦时还需要处理切向接触摩擦条件。在对钢丝绳内部应力应变进行分析时应建立相应的接触数值模型。本文从研究钢丝绳内钢丝之间的接触关系入手,定义接触主面和接触从面,并施加有限滑移接触条件,采用Augmented-Lagrangian法进行法向接触设置[11],切向采用有限滑移条件分析。

图2 钢丝绳索pro/E几何模型Fig.2 Geometric model of single-strand wire rope

图3 钢丝绳索有限元网格模型Fig.3 Finite element mesh model of single-strand wire rope
3.2 单股钢丝绳仿真结果与拉伸试验数据对比分析
利用Abaqus软件对建立的单股钢丝绳开展有限元仿真分析时,两种钢丝材料泊松比均取为0.3,所采用弹性模量见表1,分析时约束钢丝绳两端的转动自由度,同时在钢丝绳一端施加固定边界条件,另一端面施加轴向载荷。
试验采用长度为30 cm的单股钢丝绳试样,先后开展了3次破断试验,得到其平均破断载荷约为176.6 kN,试验结果列于表2中。
为验证本文有限元模型的有效性,利用有限元法对上述试验过程进行模拟分析。图4给出了分别采用有限元法和试验方法得到的钢丝绳轴向伸长量与拉力之间的对比曲线。从图4可以看出,本文有限元模型预测结果与试验结果吻合较好,初步验证了本文所建有限元模型的合理性。此外,从中还可以看出:在加载初始阶段钢丝绳轴向位移与轴向载荷之间基本保持为线性关系,当拉力增大到147 kN左右,二者不再保持为线性关系,整体上表现出“屈服”现象;可以发现此时钢丝已经发生了明显的塑性变形,进一步的加载则可能导致钢丝发生严重塑性变形甚至破断。约在180 kN时有限元模型预测位移结果显著增加,接近于试验破断力的176 kN,进一步说明有限元模型能较好地模拟钢丝绳的响应过程。

表2 单股钢丝绳拉伸破断载荷试验结果Tab.2 Results of tensile breaking load test of single-strand wire rope
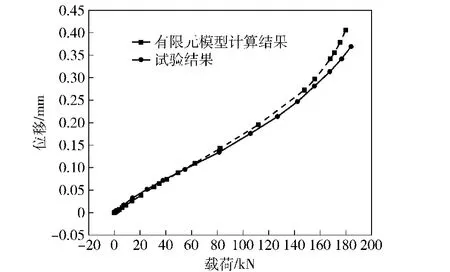
图4 有限元模型与试验所得位移-载荷对比曲线Fig.4 Load-displacement curves of finite element model and test
3.3 钢丝绳拉伸过程的弹塑性结构分析
由于本文弹塑性本构模型的塑性流动准则采用J2流动模型,而Von Mises应力是重要的评价参量,且等效塑性应变反映了塑性变形程度,因此主要讨论Von Mises应力和等效塑性应变计算结果。
图5~图7给出了不同拉伸载荷下单股钢丝绳的Von Mises应力和等效塑性应变的分布结果。其中图7给出了180.2 kN下各层钢丝的Von Mises应力分布情况,从中可以看出,在各个拉伸载荷水平下,钢丝绳内的Von Mises应力在整体上大致呈现出轴对称分布模式,应力相对较大区域出现在内侧丝并与芯丝接触的部位、外侧丝与内侧丝接触部位等。从图8可以看出,在每根钢丝内部,Von Mises应力在靠近芯股的方向较大,远离股芯的方向较小。其等效塑性应变也有类似规律。图9为钢丝绳上不同位置Von Mises应力随张力载荷变化的曲线,图10为钢丝绳上不同位置等效塑性应变随张力载荷变化的曲线。

图5 62.8 kN拉力下的钢丝绳计算结果Fig.5 FEM results of wire rope under 62.8 kN tension
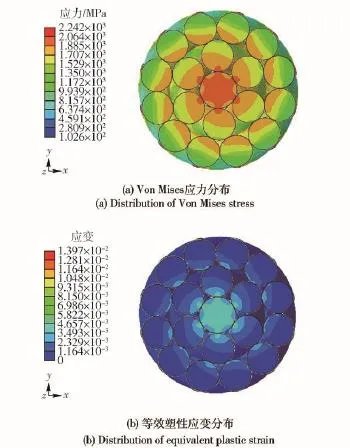
图6 147.3 kN拉力下的钢丝绳计算结果Fig.6 FEM results of wire rope under 147.3 kN tension

图7 180.2 kN拉力下的钢丝绳计算结果Fig.7 FEM results of wire rope under 180.2 kN tension
等效塑性应变分布与Von Mises应力大致类似,也是呈轴对称分布模式,塑性应变出现的部位相对较大区域出现在内侧丝并与芯丝接触的部位、外侧丝与内侧丝接触等部位。综上可知,各层钢丝之间在接触区域为危险部位,在受载过程容易发生塑性变形,这是导致该钢丝力学性能劣化和钢丝绳承载能力下降的主要原因之一。
3.4 冲击载荷下的钢丝绳结构响应仿真分析
在上述对单股钢丝绳进行静力分析的基础上,进一步开展单股钢丝绳在冲击载荷作用下的应力分析。首先通过对某型钢丝绳在单次冲击工作过程中载荷历程曲线进行平均化处理,得到便于计算的载荷-时间变化曲线,如图11所示。采用上述图3的有限元模型,运用动力学的分析方法,对钢丝绳受到轴向冲击载荷下的结构进行瞬态响应分析。

图8 180.2 kN拉力下各钢丝Von Mises应力结果Fig.8 FEM results of wire rope under 180.2 kN tension
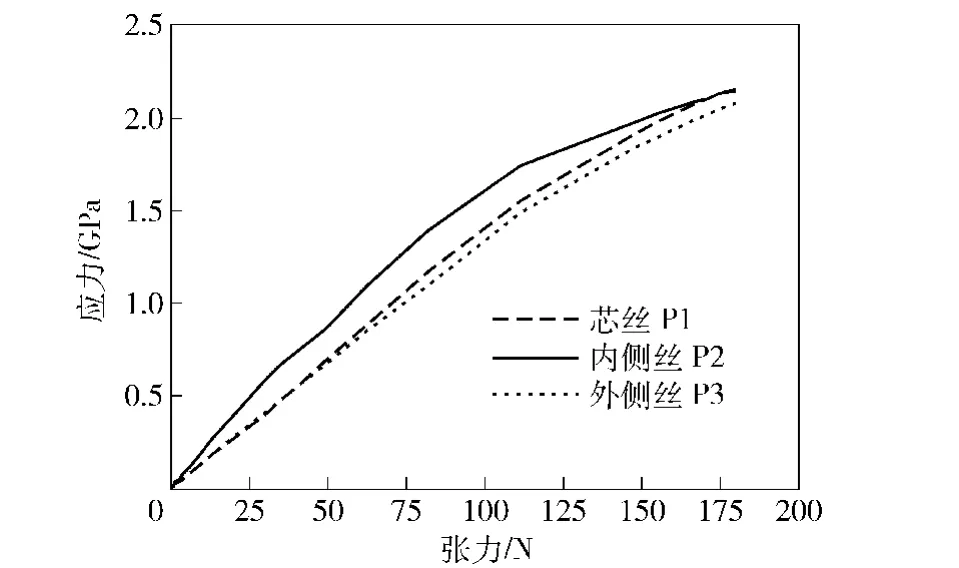
图9 钢丝绳Von Mises应力-张力载荷曲线Fig.9 Von Mises stress-tension loading curves of wire rope
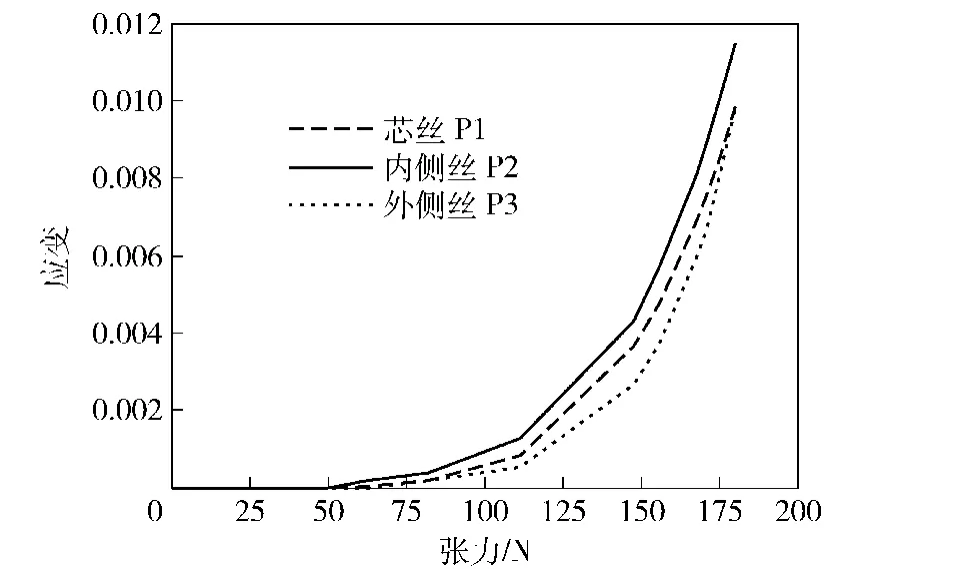
图10 钢丝绳等效塑性应变-张力载荷曲线Fig.10 Equivalent plastic strain-tension curves of wire rope

图11 钢丝绳张力载荷历程曲线Fig.11 Tension loading of wire rope
图12为单股钢丝绳在受到冲击载荷作用下钢丝绳内部不同钢丝的Von Mises应力分布,图13为冲击载荷作用下钢丝绳各丝的等效塑性应变计算结果。从图12可以看出,Von Mises应力较大位置出现在钢丝绳各钢丝与内侧钢丝接触部位,这些部位也是钢丝发生塑性变形最大的部位。
为描述单股钢丝绳内部钢丝上的Von Mises应力和等效塑性应变在冲击载荷作用时随时间的变化规律,选择钢丝绳中芯丝与内侧丝接触部位P1、内侧丝与外侧丝接触部位P2、以及外侧丝与内侧丝接触部位的P3三点位置,得到其受到一次冲击载荷作用的Von Mises应力-时间历程和等效塑性应变-时间历程如图14和图15所示。
从图14中可以看出,单股钢丝绳在受到冲击载荷作用时,其Von Mises应力与载荷曲线形状基本类似,在0.2~0.4 s之间达到最大值。而从图15中则可以看出,塑性等效应变开始产生于0.2~0.4 s之间,均对应于载荷较大的阶段,在0.4 s之后由于载荷减小,相当于部分张力的卸载,材料恢复到弹性阶段,但之前已累积产生的塑性应变为不可逆的残留应变,与金属材料的弹塑性变化规律相符。
从对于单股钢丝绳冲击载荷作用的仿真分析可以看出,在钢丝绳受到大量级的冲击载荷作用时,尽管钢丝绳没有达到破坏极限、发生破断,但是由于钢丝绳内部钢丝之间的相互作用,导致内部钢丝间应力较大的部分已经出现不可逆的塑性变形,在冲击结束后留下残留应变,降低了钢丝绳的可靠性和安全性。

图12 加载至0.26 s时各钢丝Von Mises应力分布Fig.12 Von Mises stress distribution on wire rope at 0.26 s

图13 加载至0.26 s时各钢丝等效塑性应变结果Fig.13 Equivalent distribution of plastic strain on wire rope at 0.26 s

图14 单次冲击载荷下Von Mises应力-时间曲线Fig.14 Von Mises stress-time curves under single impact

图15 单次冲击载荷下塑性等效应变-时间曲线Fig.15 Equivalent plastic strain-time curves under single impact
4 结论
1)针对钢丝绳在冲击载荷作用下内部钢丝可能会发生塑性变形的情况,采用弹塑性本构方程对钢丝绳的受力情况进行分析。
2)建立了带有内部接触的单股钢丝绳三维有限元模型,利用建立的弹塑性本构计算了在外载荷作用下单股钢丝绳内部应力应变,通过与试验结果的对比分析验证了模型的有效性。
3)通过对模型单股钢丝绳的仿真分析发现,钢丝绳内部各钢丝的Von Mises应力和塑性变形较大区域均位于接触区域,其中各钢丝又以内侧接触部位的计算结果最大,这些部位为钢丝绳塑性变形严重区域,为结构失效关注的重点部位。
4)开展了冲击载荷条件下单股钢丝绳结构弹塑性仿真分析,计算得到了在冲击载荷作用下各钢丝之间接触区域的应力应变,为进一步开展钢丝绳在冲击载荷作用下的失效分析提供了支撑。
(
)
[1] Costello G A.Stresses in multilayered cables[J].ASME Journal of Energy Resources Technology,1983,105(3):337-340.
[2] Velinsky S A,Anderson G L,Costello G A,et al.Wire rope with complex cross section[J].Journal of Engineering Mechanics,1985,52(3):380-391.
[3] Ghoreishi S R,Messager T,Cartrauda P.Validity and limitations of linear analytical models for steel wire strands under axial loading,using 3D FE model[J].International Journal of Mechanical Sciences,2007,49(11):1251-1261.
[4] 沈燕,张德坤,王大刚,等.接触载荷对钢丝微动磨损行为影响的研究[J].摩擦学学报,2010,30(4):404-408. SHEN Yan,ZHANG De-kun,WANG Da-gang,et al.Effect of contact load on the fretting wear behavior of steel wire[J].Tribology,2010,30(4):404-408.(in Chinese)
[5] Beretta S,Boniardi M.Fatigue strength and surface quality ofeutectoid steel wires[J].International Journal of Fatigue,1999,21(4):329-335.
[6] 王世文,冯继玲,杨兆建,等.弹性钢丝绳理论研究进展[J].力学进展,1999,29(4):486-500. WANG Shi-wen,FENG Ji-ling,YANG Zhao-jian,el al.Research progress on elastic wire rope theories[J].Advances in Mechanics,1999,29(4):486-500.(in Chinese)
[7] Nawrocki A,Labrosse M.A finite element model for simple straight wire rope strands[J].Computers and Structures,2000,77(4):345-359.
[8] 马军,葛世荣,张德坤.钢丝绳股内钢丝应力-应变分布的计算模型及数值模拟[J].机械工程学报,2009,45(11):277-282. MA Jun,GE Shi-rong,ZHANG De-kun.Calculating model and numerical simulation of stress-strain distribution of wires within strands[J].Journal of Mechanical Engineering,2009,45(11): 277-282.(in Chinese)
[9] 张德坤,葛世荣.钢丝微动磨损过程中的接触力学问题研究[J].机械强度,2007,29(1):148-151. ZHANG De-kun,GE Shi-rong.Research on the contact mechanisms in the process of fretting wear between steel wires[J].Journal of Mechanical Strength,2007,29(1):148-151.(in Chinese)
[10] 夏钱平,石端伟.Matlab和Pro/E在钢丝绳建模中的应用[J].机械工程师,2010(9):69-70. XIA Qian-ping,SHI Duan-wei.Modeling of the wire rope based on Matlab and Pro/E[J].Mechanical Engineer,2010(9):69-70.(in Chinese)
[11] 马军,葛世荣,张德坤.钢丝绳三维接触模型及丝间应力分布研究[J].中国机械工程,2012,23(7):864-868. MA Jun,GE Shi-rong,ZHANG De-kun.Research on three-dimensional contact model and stress distribution between wires of steel strand[J].China Mechanical Engineering,2012,23(7):864-868.(in Chinese)
Stress Analysis of Single-strand Wire Rope Based on Elastic-plastic Constitutive Model
REN Zhi-qian1,YU Zong-yue1,CHEN Xun1,WANG Yan-lei2
(1.Science and Technology on Integrated Logistics Support Laboratory,National University of Defense Technology,Changsha 410073,Hunan,China;2.Unit 92537 of PLA,Beijing 100161,China)
In order to reveal the failure of single-strand wire rope under impact load,the structural elastic-plastic attributes are analyzed by using the dimensional finite element model(FDM).According to the experiment data and wire structure,the parameters of the elastic-plastic model are determined,and a 3D FEM is established.Von Mises stress and plastic strain of the internal wire are deduced by calculating the static loading and impact loading.The results show that the Von Mises stress and plastic strain of the contact area are bigger than those of other areas,which is the main reason for the rope break.
solid mechanics;single-strand wire rope;impact loading;elastic-plastic analysis
TH142
A
1000-1093(2015)09-1782-08
10.3969/j.issn.1000-1093.2015.09.025
2014-05-27
可靠性与环境工程技术国防科技重点实验室2014年开放基金项目(KHZS20143011)
任志乾(1977—),男,讲师。E-mail:rzq_rtl@nudt.edu.cn
