推力球轴承摩擦力矩特性研究
2015-11-19邓四二贾永川
邓四二,贾永川
(1.河南科技大学机电工程学院,河南洛阳471003;2.浙江兆丰机电股份有限公司,浙江杭州311232)
推力球轴承摩擦力矩特性研究
邓四二1,2,贾永川1
(1.河南科技大学机电工程学院,河南洛阳471003;2.浙江兆丰机电股份有限公司,浙江杭州311232)
基于滚动轴承动力学理论,建立了推力球轴承动力学分析模型以及摩擦力矩数学模型,仿真分析了不同结构参数、工况参数对摩擦力矩特性的影响规律,并进行了对比验证。研究结果表明:自旋滑动产生的摩擦力矩约为推力球轴承总摩擦力矩的70%;从推力球轴承的设计角度,在保证保持架稳定性的前提下,可以适当增加钢球数和增大保持架兜孔间隙来减小轴承摩擦力矩,但钢球数对摩擦力矩的影响更为明显,且对轴承结构影响最小,应优先考虑;随着轴(座)圈沟曲率半径系数的增大,轴承摩擦力矩呈现指数形式减小,当轴(座)圈沟曲率半径系数达到0.56以后,轴(座)圈沟曲率半径系数的增大对轴承摩擦力矩影响很小,但考虑到推力球轴承的承载能力,轴(座)圈沟曲率半径系数应在0.56~0.58之间选取较为合适;从推力球轴承的使用角度,倾覆力矩、外载荷冲击量和轴承转速会对轴承的摩擦力矩产生显著影响,且外载荷冲击量的影响程度最大。
机械学;推力球轴承;动力学分析模型;摩擦力矩
0 引言
推力球轴承广泛应用于轮式装甲车减速器中,对车辆的安全性及平稳性影响较大,在此应用下使用的推力球轴承,对摩擦力矩的要求相对较高。
滚动轴承摩擦力矩特性的研究起步较晚,始于20世纪50年代,Palmgren[1]运用试验的方法得到了轴承内部润滑剂和机械摩擦引起的摩擦力矩,并将所得的试验数据按轴承类型进行汇编处理,拟合出了滚动轴承摩擦力矩回归计算公式。文献[2-4]、角田和雄[5-6]运用拟静力学的分析方法,系统分析了滚动轴承弹性滞后引起的摩擦力矩、滑动引起的摩擦力矩、流体动压引起的摩擦力矩以及球自旋引起的摩擦力矩,并试验验证了所得的理论计算公式。Townsend等[7]对轴承润滑状态与摩擦力矩的影响关系进行了理论研究和试验验证。Todd等[8]对角接触球轴承沟曲率半径系数与轴承摩擦力矩的关系进行了理论研究和试验验证。Ghanbari等[9]研究了角接触球轴承使用工况对轴承摩擦力矩的影响规律,得出了轴承转速、工作载荷与轴承摩擦力矩的关系式。邓四二等[10]基于角接触球轴承动力学和热力学分析,建立了角接触球轴承摩擦力矩理论计算公式,深入探究了轴承结构参数、工况参数对摩擦力矩的影响规律,并进行了试验验证。到目前为止,国内外学者一直热衷于球轴承摩擦力矩特性的研究[11-14],但上述研究一般都限于深沟球轴承或者角接触球轴承,缺少对推力球轴承摩擦特性的研究,鉴于此,本文针对某武器型号使用的推力球轴承,在推力球轴承动力学分析和摩擦机理研究基础上,建立推力球轴承摩擦力矩理论计算公式,分析推力球轴承结构参数和工况条件对轴承摩擦力矩的影响并加以验证。
1 推力球轴承动力学分析
图1为钢球与套圈之间作用力示意图。图1中主要坐标系为:原点位于轴承中心的惯性坐标系OXYZ和原点位于钢球质心的钢球坐标系oxyz.图1中Ωi为轴圈转速,Ωm为钢球公转速度。推力球轴承内部运动分析中,完全放弃了套圈控制理论假说,全面考虑了包括切向惯性力在内的所有惯性项,并将含有钢球自转角速度和钢球质心角速度的1阶微商各项,近似地表示为钢球方位角的函数,使其更加真实地模拟轴承动力学特性。
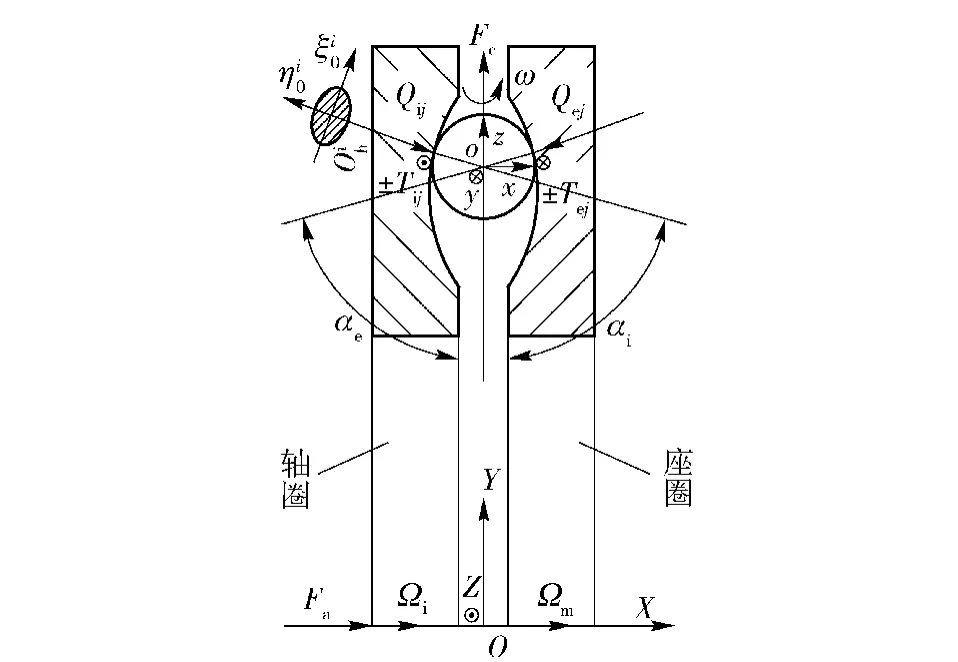
图1 钢球与套圈之间作用力示意图Fig.1 Interaction of roller and rings
1.1 推力球轴承内部零件间相互作用力
1.1.1 钢球与套圈之间作用力
推力球轴承在使用过程中受到单一方向的轴向载荷时,钢球与套圈之间的相互作用力示意图如图1所示。根据经典Hertz接触理论,第j个钢球与滚道间的法向接触力Qi(e)j可表示为两接触体间弹性趋近量δi(e)j的函数:
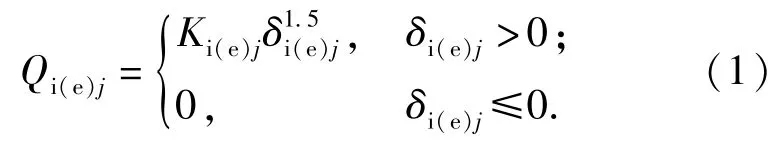
式中:Qi(e)j为第j个钢球与滚道间法向载荷;Ki(e)j为钢球与滚道接触处的负荷-变形常量;δi(e)j为第j个钢球与滚道间的弹性变形量;i、e分别表示轴圈、座圈(下同)。
该推力球轴承润滑方式采用油润滑。在轴承运转过程中,润滑油在钢球与滚道接触处形成润滑油膜,油膜对钢球在滚道上的运动起到了拖动作用。则钢球与轴圈、座圈接触面上拖动力矢量Ti(e)j可表示为

式中:g、k分别为沿接触面坐标轴ξ0和η0的单位矢量;分量Tξi(e)j、Tηi(e)j可由如下积分得到:
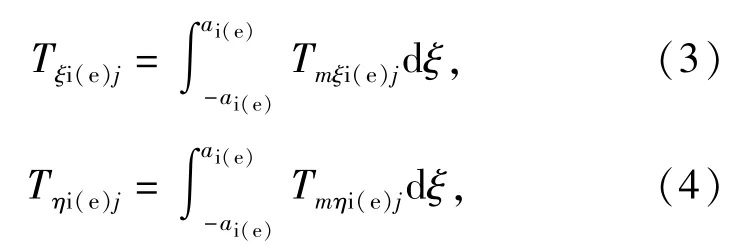
式中:Tmξi(e)j,Tmηi(e)j分别为第m个切片上沿坐标轴ξ0和η0方向的单元拖动力;ai(e)为接触椭圆长半轴。
切片上单元拖动力可表示为
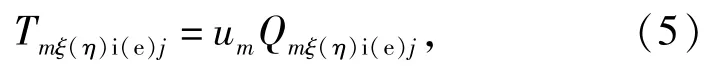
式中:Qmξ(η)i(e)j为第m个切片上的法向接触力;um为第m个切片上弹流油膜拖动系数[15]。
要建立钢球的动力学微分方程,需将钢球所受套圈的力进行分解。下面以轴圈为例,分析力的分解过程。图2为轴圈对钢球的作用力在钢球坐标系下的分解示意图。
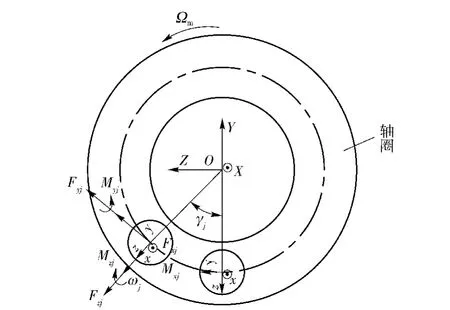
图2 轴圈对钢球的作用力在钢球坐标系下的分解示意图Fig.2 Decomposition of force applied by shaft washer on balls in coordinater system of balls
图2中:Fxj=Qijsin αij;Fyj=±Tij;Fzj=-Qijcos αij;Mxj=±0.5TijDwcos αij,Dw为钢球直径;Myj=0;Mzj=±0.5TijDwsin αij,αij为第j个钢球与轴圈之间的接触角;Qij为第j个钢球与轴圈之间的法向接触力;Tij为第j个钢球与轴圈之间的油膜拖动力。
将力Fxj、Fyj、Fzj和力矩Mxj、Myj、Mzj变换到轴承惯性坐标系中:

式中:变化矩阵

γj为第j个钢球的方位角。
同理,座圈对钢球的作用力也可作类似分解,在此不再赘述。
1.1.2 钢球与保持架之间作用力
钢球与保持架兜孔接触变形引起的作用力、钢球与兜孔之间的流体作用力以及由于保持架转速与钢球公转角速度不一致引起的碰撞力等共同影响,导致了钢球与保持架之间作用力的复杂多变。
图3为钢球与保持架兜孔之间作用力示意图。本文在SHABERTH第5代角接触球轴承模型的基础上得到钢球与保持架兜孔法向作用力Qcj:

式中:Kc=11/Cp,Cp为保持架兜孔间隙;Kn为钢球和保持架兜孔接触处的负荷—变形常量;Scj为第j个钢球中心相对于对应兜孔中心的位移。

图3 钢球与保持架兜孔之间作用力示意图Fig.3 Interaction of balls and pockets of cage
由于保持架兜孔的表面粗糙度较大,故在计算钢球与保持架兜孔之间的摩擦力时,采用的是边界润滑模型,如下式可得摩擦力Tcj:

式中:μc为边界润滑摩擦系数,
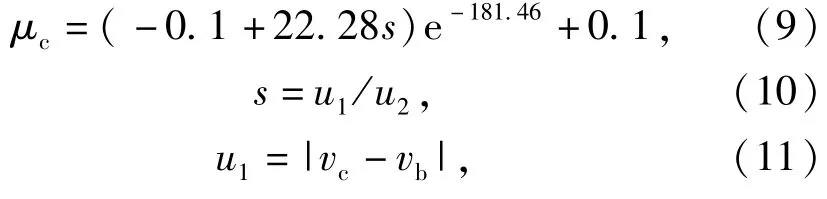
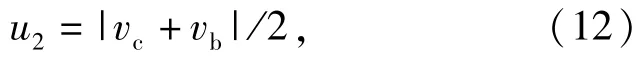
式中:s为滑滚比;vc为钢球与兜孔接触处兜孔上点的线速度;vb为钢球与兜孔接触处钢球上点的线速度;vc和vb在轴承惯性坐标系下度量。
1.2 推力球轴承动力学微分方程
基于推力球轴承内部各零件的受力及运动分析,可得轴承各个零件的动力学微分方程。
1.2.1 轴圈动力学微分方程
推力球轴承轴圈质心在平动方向的动力学微分方程:
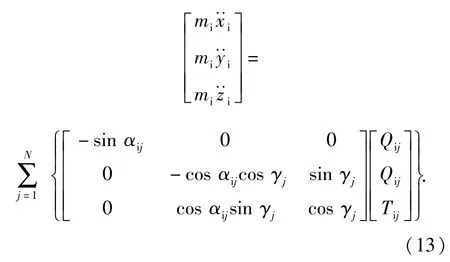
推力球轴承轴圈在转动方向的动力学微分方程:

1.2.2 钢球动力学微分方程
第j个钢球质心在平动方向的动力学微分方程:

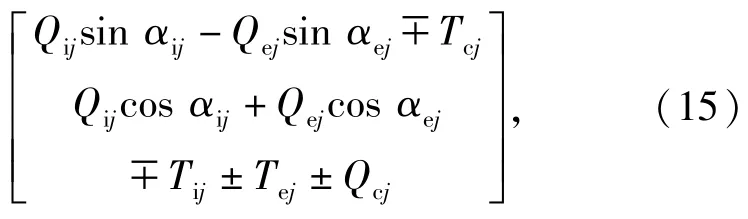
第j个钢球在转动方向的动力学微分方程:

1.2.3 保持架动力学微分方程
保持架质心在平动方向的动力学微分方程:
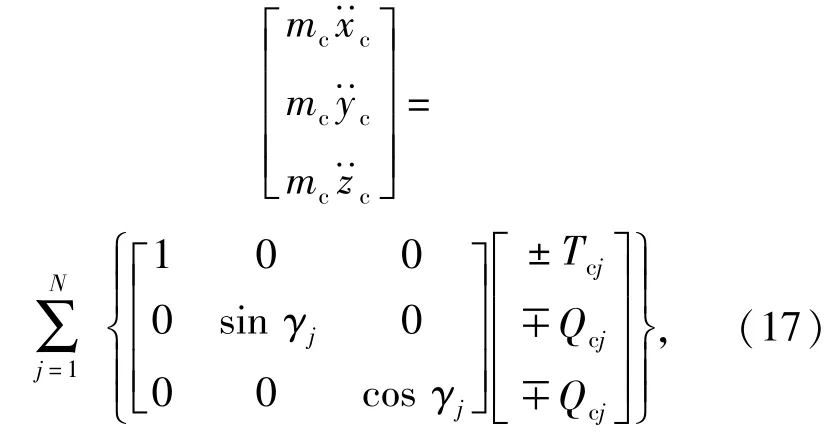
保持架在转动方向的动力学微分方程:

1.3 推力球轴承动力学微分方程的求解
依据推力球轴承动力学分析模型,编写轴承内部各元件间相互作用力子程序,采用变系数的向后微分公式(BDF)刚性积分法求解轴承的非线性动力学微分方程,可为计算后面的推力球轴承摩擦力矩理论计算式提供所需的动力学参数,并且可得到轴承运转时各元件的速度及加速度(如图4(a)、图4(b)分别为钢球公转角速度、公转角加速度随轴承运转时间的变化,图5(a)、图5(b)分别为保持架转速、保持架旋转加速度随轴承运转时间的变化)等。

图4 钢球公转角速度、角加速度随轴承运转时间的变化Fig.4 The change of revolution speed and acceleration of ball with bearing operation time
由图4和图5可知,轴承运转时钢球的公转角速度和公转角加速度、保持架转速和旋转加速度都在一定范围内波动,这会导致钢球与套圈之间的接触角、轴承各元件之间的接触载荷等也不断地发生变化,进而影响到轴承的摩擦力矩。
2 推力球轴承摩擦力矩理论计算式
推力球轴承摩擦力矩是指各种摩擦因素对推力球轴承旋转构成的阻力矩,推力球轴承的摩擦力矩是一个十分复杂的问题,它不仅与轴承本身的结构尺寸、几何精度、材料性能有关,还与工作载荷、润滑条件以及加工工艺等因素有关,根据推力球轴承内部摩擦特点,引起推力球轴承摩擦力矩的主要因素有钢球材料的弹性滞后、钢球与滚道之间差动滑动、钢球在滚道上的自旋滑动、钢球与保持架之间的摩擦和钢球与滚道之间的润滑剂粘性,上述5个因素引起的摩擦力矩总和即为推力球轴承摩擦力矩。上述各因素引起的推力球轴承摩擦力矩分量计算公式[16]如下。
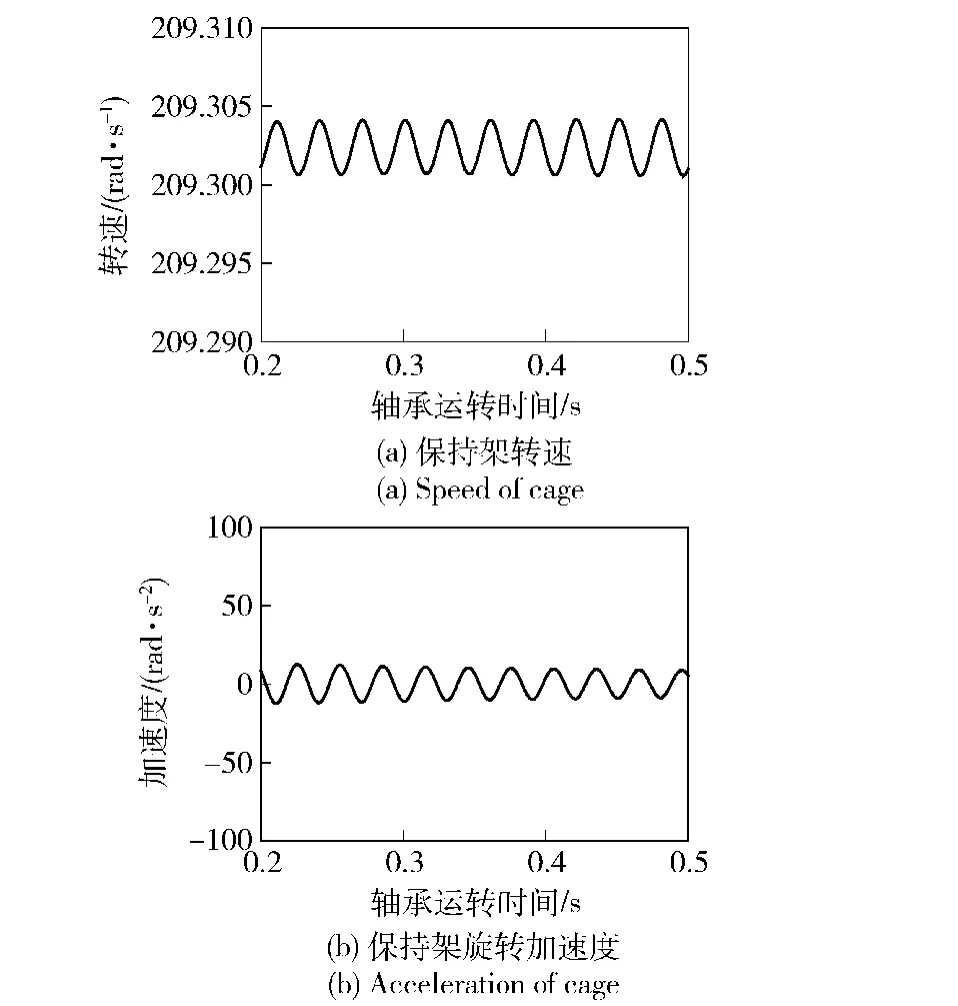
图5 保持架转速、旋转加速度随轴承运转时间的变化Fig.5 The change of speed and acceleration of cage with bearing operation time
2.1 弹性滞后引起的摩擦力矩
由于材料的弹性滞后性质,钢球在沟道上滚动时产生的滚动摩擦力矩ME为
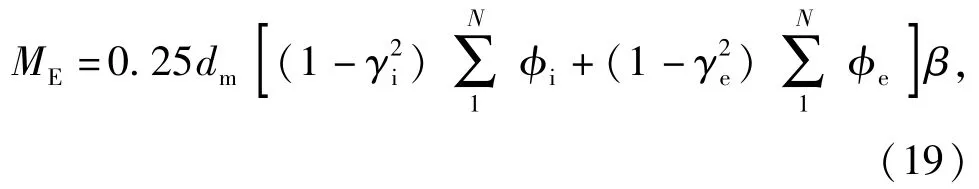
式中:dm为轴承中径;γi(e)=Dwcos αi(e)/dm,αi(e)为钢球与轴(座)圈之间的实际接触角,其值可由推力球轴承动力学分析求得;β为弹性滞后系数。
φi、φe可由下式计算:
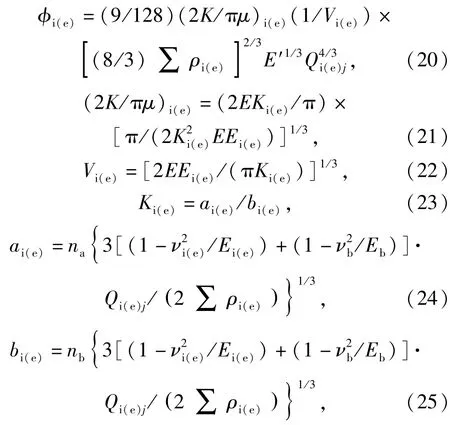

式中:ai(e)为接触椭圆长半轴;bi(e)为接触椭圆短半轴;na、nb是与轴承结构有关的参数;EKi(e)为第一类椭圆积分;EEi(e)为第二类椭圆积分;Σρi(e)为两接触面曲率和;Eb为钢球弹性模量;Ei(e)为套圈弹性模量;νb为钢球泊松比;νi(e)为套圈泊松比;Qi(e)j为第j个钢球的接触载荷。
2.2 差动滑动引起的摩擦力矩MD
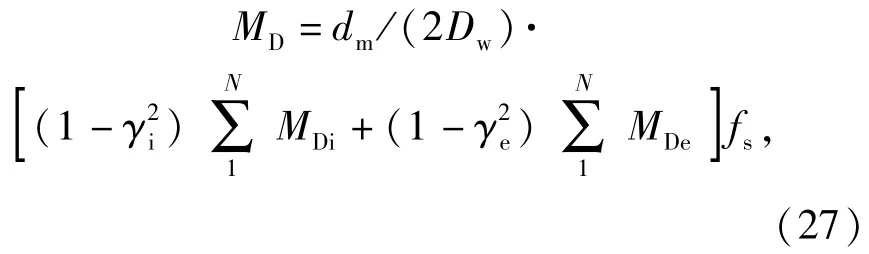
式中:fs为钢球与滚道之间的滑动摩擦系数,其值为油膜拖动系数。
MDi、MDe可由下式计算:

式中:γci(e)=fi(e)Dw/(0.5+fi(e)),fi(e)为沟曲率半径系数。
2.3 自旋滑动引起的摩擦力矩MS
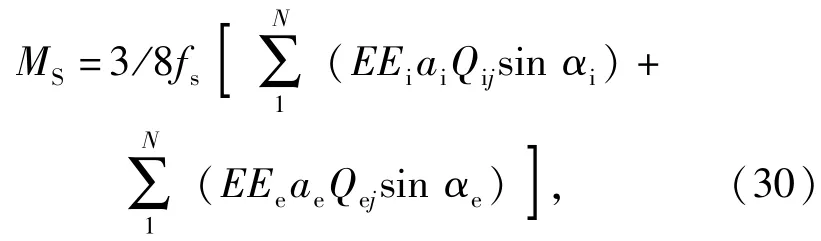
式中:αi(e)为实际工作的接触角,其值可由推力球轴承动力学分析求得。
2.4 钢球与保持架接触产生的摩擦力矩MC
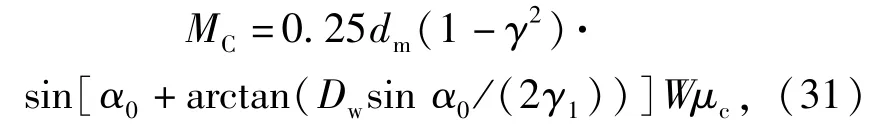
式中:γ=0.5(γi+γe);γ1=0.5dm(1-γ);α0= 0.5(αi+αe);W为保持架重量;μc为钢球与保持架之间的滑动摩擦系数,其值可由(9)式得到。
2.5 油膜粘性损失引起的摩擦力矩Moil
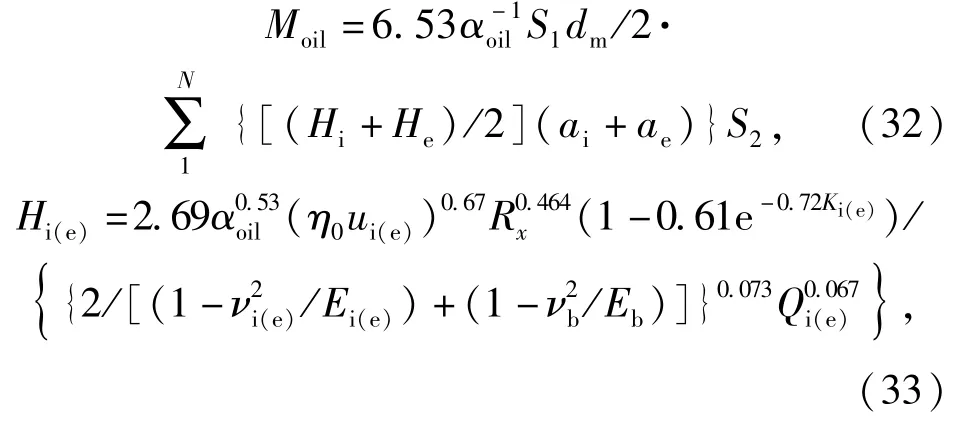
式中:Hi(e)为中心油膜厚度;η0为常压下的动力粘度;αoil为粘压系数;ui(e)为钢球与轴(座)圈接触表面的平均速度;Rx为沿钢球滚动方向的当量曲率半径;S1为润滑充分系数,可取油膜润滑系数;S2为侧漏系数,本文中没有考虑侧漏的影响,其值取为1.
2.6 总摩擦力矩
总摩擦力矩为以上5种摩擦力矩之和,即
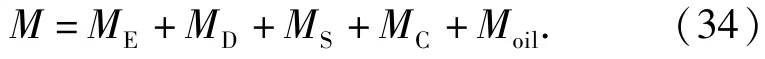
通过求解推力球轴承非线性动力学微分方程组(13)式~(18)式,求得推力球轴承动力学参数,代入(19)式~(33)式,分别求得推力球轴承摩擦力矩分量,再由(34)式即可求得推力球轴承总的摩擦力矩值。
3 推力球轴承摩擦力矩特性分析
本文以某一型号推力球轴承为例,分析了不同结构参数(钢球数、保持架兜孔间隙、沟曲率半径系数)、工况参数(轴承转速、倾覆力矩、外载荷冲击量)对轴承摩擦力矩的影响。表1为此推力球轴承的主参数。

表1 轴承主参数Tab.1 Main parameters of bearing
3.1 结构参数对轴承总摩擦力矩的影响
轴承转速为n=2 000 r/min,对其施加Fa= 2 000 N的轴向力。运用单一变量法,依次改变钢球数、保持架兜孔间隙和沟曲率半径系数,分析结构参数对轴承摩擦力矩的影响规律。
3.1.1 钢球数对轴承总摩擦力矩的影响
钢球数与推力球轴承摩擦力矩的关系如图6所示。由图6可知,影响推力球轴承摩擦力矩大小主要因素为自旋滑动,约为总摩擦力矩的70%.这是由于推力球轴承在实际运转过程中的接触角接近90°,产生的自旋分量很大,故由钢球自旋滑动产生的摩擦力矩占据了主导地位。另外从图6中可以看到,随着钢球数的增加,推力球轴承总的摩擦力矩减小,这主要是钢球数的增加,使得球上的受力减小,钢球外抛,接触角减小,随之自旋分量较小,造成总的摩擦力矩减小。但是,钢球数的增加,也造成钢球与保持架之间的滑动摩擦增加,容易导致保持架打滑。因此,从推力球轴承的设计角度来看,在保证保持架稳定性的前提下,可以适当地增加钢球数来减小轴承的摩擦力矩。
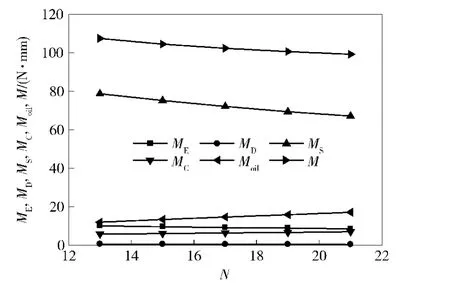
图6 钢球数与轴承摩擦力矩的关系Fig.6 Relation between number of rollers and bearing friction torque
3.1.2 保持架兜孔间隙对轴承总摩擦力矩的影响
保持架兜孔间隙与轴承摩擦力矩的关系见图7.随着保持架兜孔间隙的增大,推力球轴承摩擦力矩不断减小,这是由于保持架兜孔间隙的增大,使得钢球与保持架兜孔之间的摩擦减小。同时保持架兜孔间隙的增大,也会导致钢球与保持架之间的几何耦合失调,造成保持架运转不稳定,因此,应合理地选择保持架兜孔间隙。

图7 保持架兜孔间隙与轴承摩擦力矩的关系Fig.7 Relation between cage pocket clearance and bearing friction torque
3.1.3 沟曲率半径系数对轴承总摩擦力矩的影响
对于推力球轴承来说,轴圈和座圈的沟曲率半径系数通常是相同的,因此,本文中同时改变轴圈和座圈的沟曲率半径系数,来探究轴(座)圈沟曲率半径系数对轴承摩擦力矩的影响规律,但为了方便描述,仅列出轴圈沟曲率半径系数与轴承摩擦力矩的关系。
图8是轴承摩擦力矩、钢球与轴圈之间的接触角随轴圈沟曲率半径系数的变化规律。从中可以看到,随着轴圈沟曲率半径系数的增大,轴承摩擦力矩呈现指数形式减小。当轴圈沟曲率半径系数较小时,随着轴圈沟曲率半径系数的增大,轴承摩擦力矩大幅减小,这是由于轴圈沟曲率半径系数的增加,导致了钢球与轴圈之间的接触角增大(见图8),从而使钢球与轴圈之间的接触载荷减小,摩擦力矩减小。当轴圈沟曲率半径系数达到0.56以后,轴圈沟曲率半径系数再增大,摩擦力矩减小的幅度就很小,但是,沟曲率半径系数的增加,会导致轴承的承载能力下降。因此,考虑到推力球轴承的承载能力,轴(座)圈沟曲率半径应在0.56~0.58之间选取较为合适。
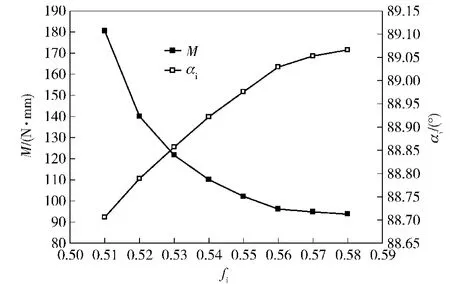
图8 轴圈沟曲率半径系数对轴承摩擦力矩、钢球与轴圈之间接触角的影响Fig.8 Effect of shaft washer groove curvature radius coefficient on baring friction torque and contact angle between ball and shaft washer
3.2 工况参数对轴承总摩擦力矩的影响
推力球轴承实际工作中存在复杂的外部工况:不同的倾覆力矩、冲击载荷及轴承转速等,导致了其摩擦力矩的多样性。分析了推力球轴承在不同工况参数下的摩擦力矩特性,得出了工况参数对轴承摩擦力矩的影响规律。
3.2.1 倾覆力矩对轴承总摩擦力矩的影响
在转速n=2 000 r/min下,对推力球轴承施加Fa=2 000 N的轴向力,通过改变单一因素—倾覆力矩,得出其对轴承摩擦力矩的影响规律。图9为倾覆力矩对轴承摩擦力矩的影响规律,图10为倾覆力矩对钢球负荷分布的影响。
由图9可知,随着轴承所受倾覆力矩的增加,轴承摩擦力矩逐渐增加,同时,增长的幅度也在不断地增加。这是由于倾覆力矩的存在,导致了各钢球受载不均匀(见图10),一部分钢球受载骤增,使得该部分钢球与滚道之间的润滑油膜厚度变薄,摩擦增大,从而整个轴承摩擦力矩增大。并且,倾覆力矩越大,钢球受载不均匀程度愈严重,轴承摩擦力矩愈大。
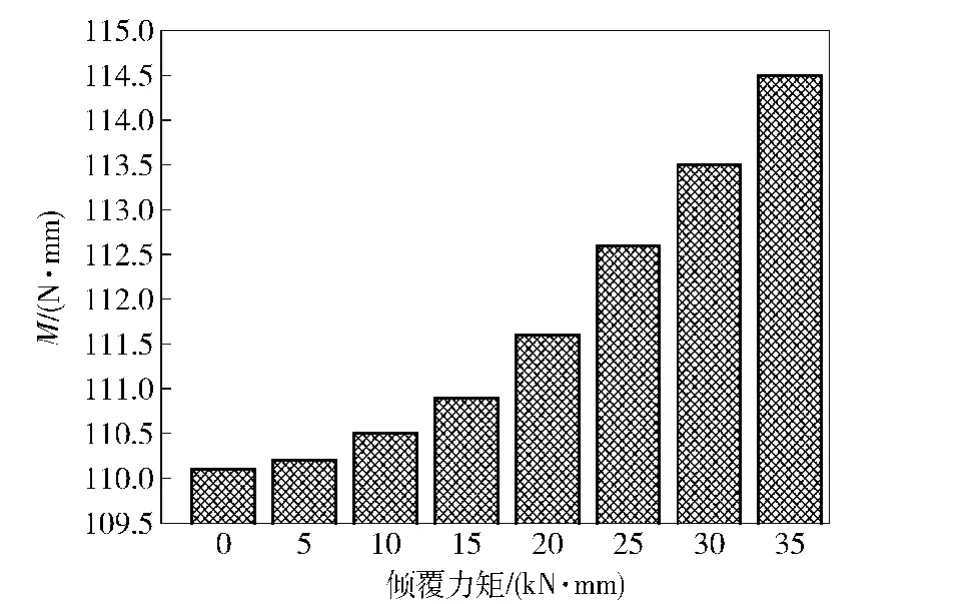
图9 倾覆力矩对轴承摩擦力矩的影响Fig.9 Effect of capsized moment on bearing friction torque

图10 倾覆力矩对钢球负荷分布的影响Fig.10 Effect of capsized moment on load distribution of balls
3.2.2 外载荷冲击量和转速对轴承总摩擦力矩的影响
推力球轴承在工作过程中,常常会遇到外载荷的瞬时变化,产生一个冲击载荷。图11为不同的外载荷冲击量F·a和转速n对轴承摩擦力矩M的影响。
由图11可得:随着外载荷冲击量、转速的增加,轴承的摩擦力矩不断增大,并且外载荷冲击量对摩擦力矩的影响更为显著。这是由于外载荷冲击量增加,会使钢球与滚道间的瞬时冲击载荷增加,钢球与滚道之间的润滑油膜厚度会急剧变薄,摩擦增大,导致整个轴承摩擦力矩增大。转速增加,钢球外抛,也会使钢球与滚道间的接触载荷增加,从而造成摩擦力矩增大。因此,为了提高寿命,推力球轴承的实际转速不宜太高,同时,应尽量避免冲击载荷的作用。

图11 外载荷冲击变化量和轴承转速对摩擦力矩的影响Fig.11 Effect of impact load and bearing rotational speed on bearing friction torque
4 推力球轴承总摩擦力矩数学模型验证
采用SKF专用滚动轴承性能分析软件计算结果与本文分析模型计算结果进行对比验证。推力球轴承主要参数:轴承内径75 mm,轴承外径110 mm,轴承宽度24.6 mm,钢球直径13.493 8 mm,钢球数19.轴承工况条件为轴向负荷2 000 N.不同转速下,本文分析结果和SKF专用滚动轴承性能分析软件计算结果如表2所示。
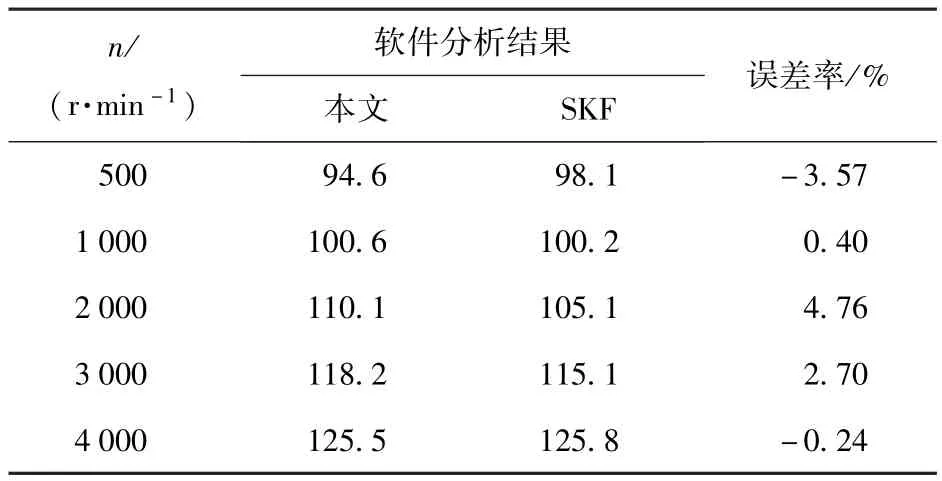
表2 计算结果对比Tab.2 Comparison of calculated resultsN·mm
由表2可知:本软件与SKF专用滚动轴承性能分析软件计算结果基本相似,轴承摩擦力矩误差率不超过±5%,说明本文所建立的模型能较准确地描述推力球轴承的摩擦力矩。
5 结论
本文基于滚动轴承动力学分析理论,建立了推力球轴承动力学分析模型以及摩擦力矩数学模型。分析了不同结构参数和工况参数对轴承摩擦力矩的影响规律,得出以下结论:
1)自旋滑动产生的摩擦力矩在推力球轴承总的摩擦力矩中占据了主导地位,约为总摩擦力矩的70%.
2)从推力球轴承的设计角度,在保证保持架稳定性的前提下,可以适当的增加钢球数和增大保持架兜孔间隙来减小轴承摩擦力矩,但钢球数对摩擦力矩的影响更为明显,且对轴承结构影响较小,应优先考虑。
3)随着轴(座)圈沟曲率半径系数的增大,轴承摩擦力矩呈现指数形式减小。当轴(座)圈沟曲率半径较小时,随着轴(座)圈沟曲率半径系数的增大,轴承摩擦力矩大幅减小;当轴(座)圈沟曲率半径系数达到0.56以后,轴(座)圈沟曲率半径系数再增大,轴承摩擦力矩减小的幅度就很小,但是,沟曲率半径系数的增加,会导致轴承承载能力下降。因此,考虑到推力球轴承的承载能力,轴(座)圈沟曲率半径系数应在0.56~0.58之间选取较为合适。
4)从推力球轴承的使用角度,倾覆力矩、外载荷冲击量和轴承转速会对轴承的摩擦力矩产生显著影响,且外载荷冲击变化量的影响程度最大。
(
)
[1] Palmgren A.Ball and roller bearing engineering[M].Burbank: Philadephia,1959.
[2] Snare B.Rolling resistance in lightly loaded bearings[J].The Ball Bearing Journal,1968,152:3-8.
[3] Snare B.Rolling resistance in loaded roller bearings[J].The Ball Bearing Journal,1968,153:19-24.
[4] Snare B,Eng G.Rolling resistance in loaded ball contacts[J]. The Ball Bearing Journal,1968,154:3-14.
[5] 角田和雄.玉軸受の摩擦発生機構(1)[J].機構學,1965(2): 645-648. Kakuta Kazuo.Generating mechanical of friction torque in a ball bearing(1)[J].Mechanism,1965(2):645-648.(in Japanese)
[6] 角田和雄.玉軸受の摩擦発生機構(2)[J].機構學,1965(3): 645-648. Kakuta Kazuo.Generating mechanical of friction torque in a ball bearing(2)[J].Mechanism,1965(3):645-648.(in Japanese)
[7] Townsend D P,Allen C W,Zaretsky E V.Study of ball bearing torque under elastohydrodynamic lubrication,NASA-TM-X-68271[R].Cleveland,Ohio:National Aeronautics and Space Administration,Lewis Research Center,1973.
[8] Todd M J,Stevens K T.Frictional torque of angular contact ball bearings with different conformities,ESA-CR(P)-1221[R]. Risley:National Center of Tribology,European Space Tribology Lab,1978.
[9] Ghanbari A,Khanmohamadi S.A new test rig for friction torque measurement in ball bearing[J].WSEAS Transactions on Systems,2006,9:2172-2177.
[10] 邓四二,李兴林,汪久根,等.角接触球轴承摩擦力矩特性研究[J].机械工程学报,2011,47(5):114-120. DENG Si-er,LI Xing-lin,WANG Jiu-gen,et al.Frictional torque characteristic of angular contact ball bearings[J].Journal of Mechanical Engineering,2011,47(5):114-120.(in Chinese)
[11] DENG Si-er,TENG Hong-fei,WANG Yan-shuang,et al.Constitutive equation of a new aviation Lubricating oil[J].Chinese Journal of Mechanical Engineering,2007,17(5):28-31.
[12] Kanatsu M,Ohta H.Running torque of ball bearings with polymer lubricant(running torque formulae)[J].Transactions of the Japan Society of Mechanical Engineers:Part C,2005,71(1): 272-279.
[13] Leblanc A,Nelias D.Ball motion and sliding friction in a four-contact point ball bearing[J].Journal of Tribology,2007,129(4): 801-808.
[14] Kanatsu M,Ohta H.Running torque of ball bearings with polymer lubricant(running torque formulas of deep groove ball bearings under axial loads)[J].Journal of Tribology,2008,130(4): 041507.
[15] WANG Yan-shuang,YANG Bo-yuan,WANG Li-qin.Investigation into the traction coefficient in elasto-hydrodynamic lubrication[J].Tribotest,2004,11(2):113-124.
[16] 张葵,李建华.球轴承摩擦力矩的分析计算[J].轴承,2001(1): 8-11. ZHANG Kui,LI Jian-hua.Analysis of friction torque on ball bearings[J].Bearing,2001(1):8-11.(in Chinese)
Friction Torque Characteristics of Thrust Ball Bearings
DENG Si-er1,2,JIA Yong-chuan1
(1.School of Mechatronics Engineering,Henan University of Science and Technology,Luoyang 471003,Henan,China;2.Zhejiang Zhaofeng Mechanical and Electronic Co.,Ltd.,Hangzhou 311232,Zhejiang,China)
The dynamic analysis model and the mathematical model of the friction torque of thrust ball bearings are obtained based on the dynamic theory of rolling bearing.The effects of the structural parameters and operating conditions on the frictional torque of thrust ball bearings are analyzed and verified.The results show that the friction torque caused by spin-sliding is approximately 70%of the total friction torque of the thrust ball bearings.From the perspective of the design of the thrust ball bearings,the friction torque can be reduced by increasing the number of balls and the cage pocket clearance appropriately on the premise that the stability of the cage can be ensured.However,the priority should be given to the number of balls,which has more obvious effect on the friction torque and minimal influence on the bearing structure.With the increase in groove curvature radius coefficient of shaft(house)washer,the bearing friction torque decreases in exponential form.The groove curvature radius coefficient of shaft(house)washer has a little effect on the friction torque when its value is over 0.56.In consideration of the bearing carrying capacity,the groove curvature raidus coefficient of shaft(house)washer is better between 0.56and 0.58.From the perspective of the use of the thrust ball bearings,the capsized moment,impact load and rotation speed have great effect on friction torque,but the influence of the impact load on it is the worst.
mechanics;thrust ball bearing;dynamic analysis model;friction torque
TH133.33+1
A
1000-1093(2015)09-1615-09
10.3969/j.issn.1000-1093.2015.09.003
2014-09-19
国家“十二五”科技攻关项目(JPPT-ZCGX1-1);河南省科技创新人才计划项目(144200510020)
邓四二(1963—),男,教授,博士生导师。E-mail:dse@haust.edu.cn;贾永川(1988—),男,硕士研究生。E-mail:jyc860527@163.com
