1种N-dot过渡态PI控制律的设计方法

王 曦，党 伟，李志鹏，胡忠志，殷 铠，张 荣

（1.北京航空航天大学能源与动力工程学院，北京100191；2.先进航空发动机协同创新中心，北京100191；3.中国商用航空发动机有限责任公司，上海200108；4.中航工业航空动力控制系统研究所，江苏无锡214063）

0 引言

几十年来，工程上常采用开环油气比（Wf/Ps3）的设计方法实现航空发动机慢车以上过渡态加减速控制和起动过渡态加速控制，如ΑЛ-31Φ 双转子加力涡扇发动机。这种控制律存在以下问题：发动机性能会随着飞行时数的延长，或因发动机制造、加工、装配等原因，出现不同程度的退化和衰减，按油气比的加减速控制律设计的控制器会使过渡态性能降低，最终影响飞机的性能；另外，在发动机起动过程中，油气比加速起动控制律性能的好坏随不同的地域、气候环境条件变化，在平原地区可能成功率高，但在高原环境条件下，起动成功率可能很低；在温和的春、秋季环境条件下，起动性能可能很好，但在炎热的夏季或寒冷的冬季，起动性能可能变得很差，这显然难以满足飞机对发动机起动性能的技术要求。

相比油气比过渡态控制律，欧美国家普遍使用N-dot闭环控制律[1-3]，其最突出的优点在于能够把握发动机过渡态期间的非线性时变特性，按能够代表发动机时变特性的转速变化率设计闭环加速控制律，实现按发动机转子转速加速度的需求自动调节燃油流量以匹配发动机涡轮和压气机在不同环境条件下所具有的剩余功率，充分反映发动机的过渡态所要求的本质特性，从根本上克服上述油气比开环控制律中存在的内在缺陷，而不会因发动机制造、加工、装配的不确定性以及元器件老化导致的性能退化和衰减影响过渡态加减速性能。此外，该方法还可以使发动机在起动过渡态下具有更好的环境适应性。

本文针对N-dot闭环控制律的设计问题进行了方法性的探讨，采用PI控制器构建了N-dot闭环控制回路，基于差分进化算法对性能约束优化目标进行求解，获得了N-dot闭环PI控制器参数的优化结果。在设计过程中考虑了执行机构、传感器、滤波器的动态特性，以考察与工程相一致的设计效果。最后，与油气比开环过渡态控制律的性能进行了仿真对比，结果显示，这种方法能显著地提高发动机的过渡态性能。

1 N-dot闭环PI控制器

1.1 N-dot闭环PI控制回路结构

以双转子不加力分开排气喷口不可调涡扇发动机为研究对象，构建N-dot闭环PI控制回路（考虑到PI控制的结构简单，本文未采用相对结构较为复杂的PID控制方案），如图1所示。考虑到发动机过渡态的非线性时变特性，为使其具备更好的加减速环境适应性，将N-dot加减速控制计划设计为发动机进口温度和高压转子转速的函数[2]。

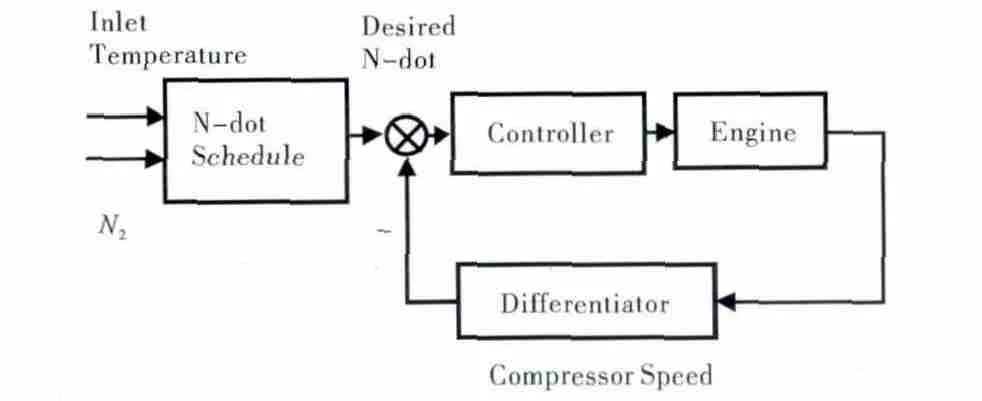
图1 N-dot闭环PI控制回路结构

过渡态控制有多种控制器设计方案可供选择，如滑模控制[6]、模糊控制[7]等，为使过渡态控制与稳态控制易于切换，并考虑到切换前后不同的抗积分保护效果，采用PI结构能够在切换过程中通过积分冻结处理达到这一设计目标。

1.2 差分进化算法

N-dot前向回路中存在1个虚轴上的零点，且控制回路中不可避免地存在非线性特性，如执行机构的位置饱和、速率饱和等非线性特性等，本文选择差分进化优化算法进行设计。

差分进化算法是遗传算法的变种，其原理简单易实现、收敛速度快，是1种不需要初始信息就可以寻求全局最优解的优化方法。该算法基于种群内的个体差异度生成临时个体，然后随机重组实现种群进化，具有很好的全局收敛性和鲁棒性。差分进化算法包括初始化、变异操作、交叉操作和选择操作几部分[11]，具体流程如图2所示。差分进化算法中的设置参数（如种群数量NP、变异算子F、交叉算子CR等）的选取对差分进化算法的性能有着重要影响。

鉴于差分进化算法的优化效果，对求解N-dot闭环PI控制器的参数进行探讨。

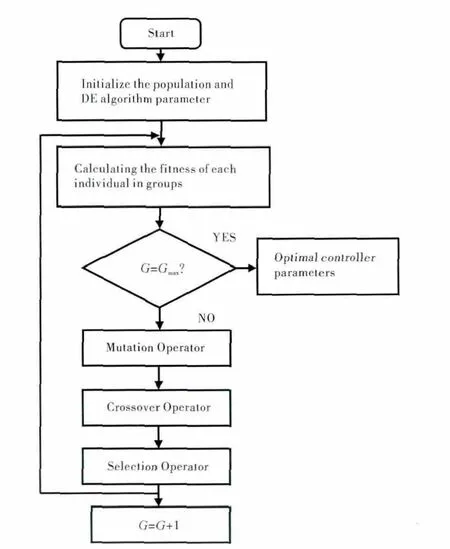
图2 差分进化算法流程

2 PI控制器的差分进化优化

发动机动态特性主要由机械转子动力学的惯性效应和温度动力学的能量储存效应决定[4]。温度动力学的能量存储效应由容腔内燃气热力学状态改变引起的快速温度变化和发动机热端金属部件与燃气之间的热传导引起的慢速温度变化构成，其动态响应时间相差1个数量级以上。考虑到本文研究的涡扇发动机在动态变化过程中，其动态特性主要受到高低压转子转速的惯性、温度变化范围大的高压涡轮机匣温度以及高压涡轮叶片温度的热惯性影响，同时考虑到燃油执行机构动态特性是时间常数为0.05s的惯性环节，与其串联后增广为具有5阶动态的被控对象传递函数，在飞行高度为0、飞行马赫数为0，且发动机工作在慢车状态的情况下，从控制器输出的燃油流量指令到发动机高压转子转速的传递函数为

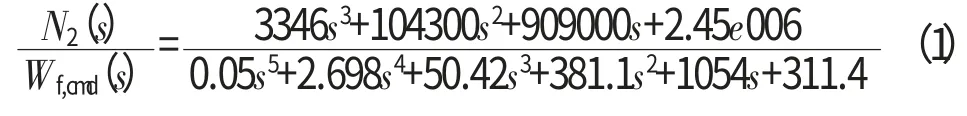
式中：N2为发动机高压转子转速，r/min；Wf,cmd为燃油流量指令，kg/h。

伺服跟踪的物理意义是要求发动机转速响应相对于目标指令转速的上下偏差分布，为了在优化过程中保证伺服跟踪性能和控制能量不出现非线性饱和限制问题，在优化目标中可采用对偏差取绝对值的加权，对控制输出取绝对值的加权反映对控制能量的限制，能有效防止控制输出的非线性饱和，反馈设计优化目标为

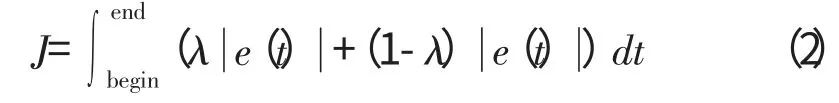
考虑到上述被控对象传递函数中零点、极点的分布，选择差分算法PI参数的搜索范围为

设种群数量为NP=100，变异算子F=1.2、交叉算子CR=0.9，最大迭代次数G=50，加权因子λ=0.99。

PI控制器采用上述差分进化算法所求优化参数结果为Kp=0.00105734 Ki=79.545。

按照上述差分进化算法求解的PI控制器仅适用于某一稳态工作点，而加速过渡态的范围起于慢车状态止于最大状态，对于这种参数变化较大的过渡态特性，用1个控制器很难满足其要求。因此，采用分段设计再增益调度的方法，从慢车状态到最大状态选择了4个稳态工作点进行设计，设计结果见表1。N-dot加速控制器以发动机转子转速对其进行增益调度，即按插值或区域切换的方法可获得适用于整个过渡态工作范围的N-dot加速控制器。

表1 4个工作点对应的控制器参数

在过渡态下N-dot控制以发动机转子转速的变化率为设计目标，未考虑加减速过渡态下发动机可能出现的压气机喘振、高压涡轮进口超温的问题，N-dot控制自身不具备防止发动机进入喘振、超温、熄火的能力，发动机过渡态下转子转速加速率的限制边界条件如图3所示[4]。

考虑如图3所示的加减速过程中喘振、超温、熄火边界条件的的安全裕度限制，可得N-dot控制计划，如图4所示。

图3 发动机过渡态转速加速率限制边界条件

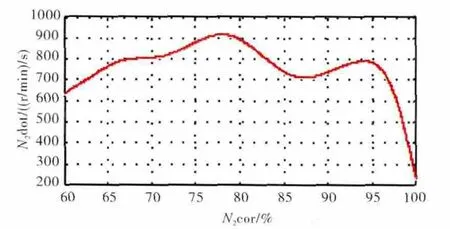
图4 N-dot控制计划

3 仿真分析

为了验证N-dot控制器的过渡态加速性能，构建如图5所示的包含稳态控制和过渡态控制的仿真结构，并加入Wf/Ps3油气比加速规律，用来比较各自的加速控制性能。稳态与过渡态的状态切换采用低选逻辑设计，同时针对不同状态控制器工作时出现的积分饱和问题，采用积分冻结的抗积分保护策略，即在稳态控制器工作时，冻结N-dot加速控制器；而当N-dot加速控制器工作时，冻结稳态控制器。

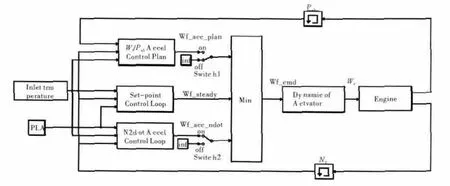
图5 N-dot控制仿真结构

设高压压气机和高压涡轮的效率均损失5%，按图5的切换方式，置Wf/Ps3油气比加速控制为关闭状态，接通N-dot控制器，作为Wf/Ps3油气比加速验证方案1；置N-dot控制器为关闭状态，接通Wf/Ps3油气比加速控制，作为N-dot控制器验证方案2；在地面状态下，从慢车状态的第5s开始快推油门杆，在1s内将油门杆推到最大状态的位置，分别按方案1和方案2在压气机和涡轮的效率均处于未衰减状态的情况下，按Wf/Ps3油气比加速供油规律加速与按N-dot闭环控制规律加速获得的加速过程燃油流量动态响应曲线如图6所示。2种工作方式下的燃油加速供油曲线比较接近，在第8s时完成从加速过程到稳态过程的切换，随后进入最大状态的稳态控制。在压气机和涡轮的效率均衰减5%的情况下，按方案1油气比加速供油规律工作所得的燃油流量仿真曲线与按方案2的N-dot闭环控制器工作所得的燃油流量仿真曲线的对比如图7所示。通过对比2种不同的加速控制方案下供油量的变化（图6和图7）中看出，发动机效率降低时，采用油气比加速供油规律的供油明显不足，不能充分发挥发动机的潜能。

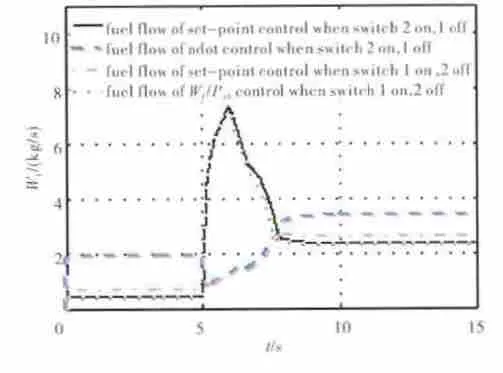
图6 2种工作情况下的燃油加速供油曲线

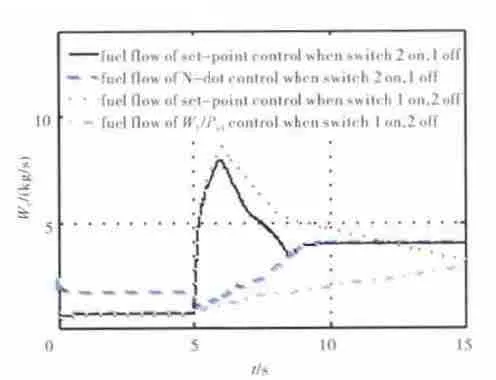
图7 在压气机、涡轮效率衰减5%的情况下，2种方式下燃油加速供油曲线

在2种不同的加速方案下高压转子转速N2、排气温度EGT(exhaust gas temperature)以及压气机喘振裕度响应曲线分别如图8~10所示。其中图（a）为N-dot控制律的工作情况，图（b）为油气比开环供油规律的工作情况，图（a）、（b）都加入了与发动机正常工作效率情况下的对比以验证控制策略的好坏。对比图8（a）、（b）可知，采用N-dot闭环控制器的加速控制方案时，无论气机和涡轮的效率是否有衰减，加速效果基本一致；而采用油气比加速供油规律时，在压气机机和涡轮的效率出现衰减的情况下，加速性能明显变差。但是，采用N-dot闭环控制器的加速控制方案会带来排气温度的升高，压气机喘振裕度的减小，且变化程度大于采用油气比加速控制方案时的情况，如图9、10所示。因此在采用N-dot闭环控制器的加速控制方案时必须做好对各种参数（如转速、排气温度及喘振裕度等）的限制，即顶层管理，或称为限制保护控制。

图8 2种方式工作情况下高压转子转速响应对比

图9 2种方式下排气温度响应对比

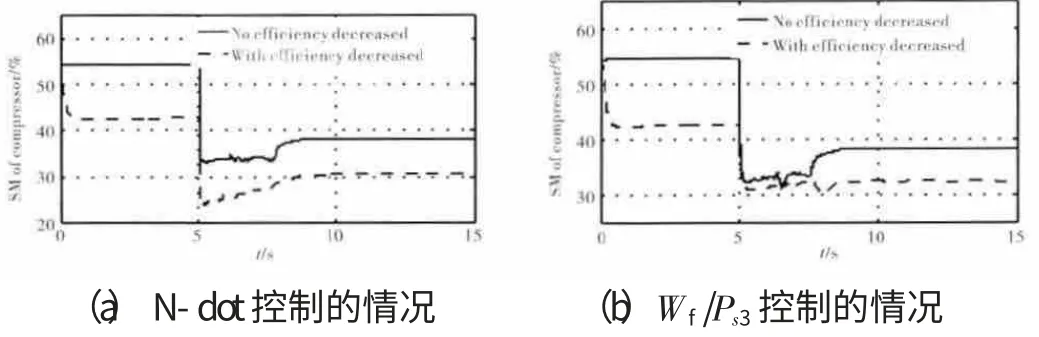
图10 2种方式下压气机喘振裕度响应对比

在加速过程中N-dot在发动机效率正常及衰减2种工作方式下的响应对比情况如图11所示。图中实线为N-dot控制指令曲线，虚线为压气机和涡轮的效率在正常情况下和有衰减情况下的N-dot响应曲线。N-dot控制采用了闭环策略，在加速过程中，控制策略不受发动机性能退化的影响，通过N-dot控制可以自发调节燃油流量保证N-dot信号的伺服跟踪，进而保证了发动机的加速性能不变。

在压气机特性线上，绘制出采用N-dot闭环和油气比开环2种工作方式下的加速工作线，如图12所示。从图12（a）中可见，在N-dot控制律的加速情况下，当压气机和涡轮的效率衰减后，加速线更靠近喘振线和排气温度限制线，而采用Wf/Ps3油气比供油规律的加速线基本与压气机和涡轮的效率未衰减情况下的加速线一致，这进一步论证了以上分析的正确性。

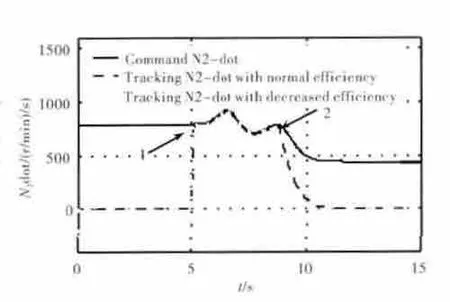
图11 在加速过程中N-dot在2种工作方式下的响应对比

图12 在压气机特性线上反映的2种工作方式下的加速工作线

上述仿真对比分析表明：不论发动机性能是否退化，采用N-dot闭环加速控制的策略，都能保证加速性能为最优，但是喘振裕度和排气温度裕度均有减小；与此相反，采用Wf/Ps3油气比开环供油规律的加速控制策略，虽然喘振裕度和排气温度裕度减小不大，但不能保证加速快速性能。

发动机控制包括稳定控制、过渡态控制和限制保护控制（顶层管理）3部分。在工程实际中，限制保护控制逻辑保证了关键的气动热力参数不超出一定工作范围，与N-dot加速控制策略配合，共同完成期望加速过渡态控制，使得这些关键参数在加速过程中能够保证各自的安全裕度，同时获得不随发动机性能退化而变化的加速性能。为了反映N-dot加速控制的真实效果，在上述仿真中未加入压气机喘振裕度限制和排气温度限制的保护控制逻辑。

4 结论

提出了1种基于差分进化算法设计N-dot加速控制律的方法，并采用增益调度的策略对双转子不加力分开排气喷口不可调涡扇发动机设计了N-dot闭环加速控制器。在发动机性能退化的情况下与以Wf/Ps3油气比开环供油规律的加速性能进行了仿真对比，结果表明N-dot加速控制律不会因发动机性能的退化程度而降低加速性能。

在后续研究中，将考虑发动机气动热力参数的限制保护逻辑设计问题，以构建完整的N-dot加速控制律。

[1]Parsons.D A.N-dot schedules dynamic compensation system for gas turbines-inputs sum of speed and rate of change of speed of gas generator to schedule to output desired acceleration as function of generator speed：US,5029441[P].1991-7-9.

[2]Merrill W，Lehtinen B，Zeller J.The role of modern control theory in the design of controls for aircraft turbine engines[J].Journal of Guidance，Control and Dynamics，1984，7（6）：652-661.

[3]Spang HA，Brown H.Control of jet engines[J].Control Engineering Practice，1999，7（9）：1043-1059.

[4]Link C J，Jack D M.Aircraft engine controls：design，system analysis，and health monitoring[M].Alexander：American Institute of Aeronautics and Astronautics，2009：118-124.

[5]Deore P J，Patre B M.Design of robust compensator for jet engine：an interval analysis approach[C]//Control Applications,Proceeding of 2005 IEEE Conference，Toronto，2005：376-381.

[6]Hanz R A.Multi-regulator sliding mode control strategy for output-constrained systems[J].Automatica，2011，47（10）：2251-2259.

[7]董劲，黄金泉.航空发动机多变量模糊PID控制[J].航空动力学报,2003,18（4）:538-541 DONG Jin,HUANG Jinquan.Multivariable fuzzy-PID control for aeroengine[J].Journal of Aerospace Power,2003,18（4）:538-541.（in Chinese）

[8]Rainer Storn，Kenneth Price.Differential evolution-a simple and efficient adaptive scheme for global optimization over continuous spaces[J].Journal of Global Optimization，1997，22（11）：341-359.

[9]吴亮红，王耀南，袁小芳，等.自适应二次变异差分进化算法[J].控制与决策，2006，21（8）：898-903.WU Lianghong，WANG Yaonan，YUAN Xiaofang，et al.Differential evolution algorithm with adaptive second mutation[J].Control and Decision，2006，21（8）：898-903.（in Chinese）

[10]WU Lianghong，WANG Yaonan，ZHOU Shaowu，et al.Design of PID controller with incomplete derivation based on differential evolution algorithm[J].Journal of Systems Engineering and Electronics，2008，19（3）：578-583.

[11]Montazeri-Gh M，Jafari S.Evolutionary optimization for gain tuning of jet engine min-max fuel controller[J].Journal of Propulsion and Power，2011，27（5）：1015-1023.

[12]KONG Xiangxing，WANG Xi，TAN Daoliang,et al.An extrapolation approach for aero engine’s transient control law design [J].Chinese Journal of Aeronautics，2013，26（5）：1106-1113.

[13]Price K V.Differential evolution：a fast and simple numerical optimizer[C]//Biennial Conference of the North American，New York:1996：524-527.

[14]Eberhart R C，Kennedy J.A new optimizer using particle swarm theory [C]//Proceeding of the Sixth International Symposium on，Nagoya：Micro Machine and Human Science，1995：39-43.

[15]Richter H.Advanced control of turbofan engines[M].New York：Springer，2011：78-82.