航空发动机叶尖间隙数学模型的建立与验证

陈 研，吕天波，张 生，张 镭

（1.中航工业沈阳发动机设计研究所，沈阳110015；2.东北大学 机械工程与自动化学院，沈阳110819）

0 引言

先进的气动设计与试验方法使航空发动机压气机和涡轮的效率已经达到很高水平，为了进一步提高其效率，除注重气流参数选择外，还应减小叶尖间隙损失。这种损失是由转子叶片和机匣间的间隙造成的。虽然可用计算机模型来预测叶尖间隙，但这种预测必须由试验数据来验证和细调。所以在航空发动机研制过程中，叶尖间隙是1个基本的测量参数。叶尖间隙过大，会降低发动机的效率，增加耗油率；但叶尖间隙也不能过小，因为过小的间隙有可能危及发动机的安全。因此必须严格控制叶尖间隙和测量叶尖间隙，使发动机处于最佳的运行状态。目前，对发动机叶尖间隙研究主要采用通过测试设备测得发动机工作时的叶尖间隙值的试验分析方法，近年来国内航空研究机构开发了多种间隙测量方法，常用的有火花放电法、涡电流法、激光光学法、电容法、微波法、超声波法以及光纤法等。

但是目前国内的研究还停留在测量叶尖间隙数据层面上，还没有针对测得的叶尖间隙数据处理开展相关研究工作。本文在国内率先进行了叶尖间隙数据处理的理论研究，并建立了相关数学模型。

1 叶尖间隙单传感器单步法数学模型的建立

1.1 叶尖间隙单传感器单步法概述

航空发动机叶尖间隙的形成和大小主要受机匣表面轮廓半径方向变动量、几何中心位置、转子的回转中心变动量以及转静子平均半径差等因素影响，有效地将这些因素进行分离对间隙的形成和变化规律的研究有非常关键的作用。

若要实现各要素的真正分离，目前可采用频域法和时域法。这2种方法都要求在采样过程中测量数据的冗余，即要求通过多传感器1次转位或单传感器多次转位获取采样数据。然而，由于目前实际硬件只能提供单传感器跟随转子旋转1周测量发动机叶尖间隙数据的测试条件，既无法将所有要素完全真正分离，所以在建立数学模型之前，认为静子机匣为理想轮廓，发动机转静子叶尖间隙仅由转、静子的中心位置和平均半径差以及转子的回转误差构成。

1.2 叶尖间隙最小二乘中心法数学模型的建立

在单传感器单步法中，要求得到最主要的1个参数是最小二乘圆心对回转中心的偏移量，即偏心值。偏心值的大小直接决定发动机转静子装配是否合格，具有实际工程意义。下面基于最小二乘中心法来建立叶尖间隙的数学模型，如图1所示。以测量时被测截面的回转中心Ol为圆心，将被测实际圆分成m个彼此相等的角度，于是得到m个从Ol算起的实际圆半径ri（i=1，2，…，m）。这m个半径与被测实际圆的交点为Pi（i=1，2，…，m）。在以Ol为极坐标系的圆点的极坐标系中，令最小二乘圆的圆心为O，半径为R，最小二乘圆圆心与回转中心的偏离量为e，各离散采样点Pi到最小二乘圆之径向偏离量为εi（i=1，2，…，m），各等分采样点Pi至回转中心Ol的连线OlPi与极坐标轴的夹角为θi（i=1，2，…，m）。

在ΔOOlP 中，Pi=εi，OlPi=ri，OPi=R+εi，则

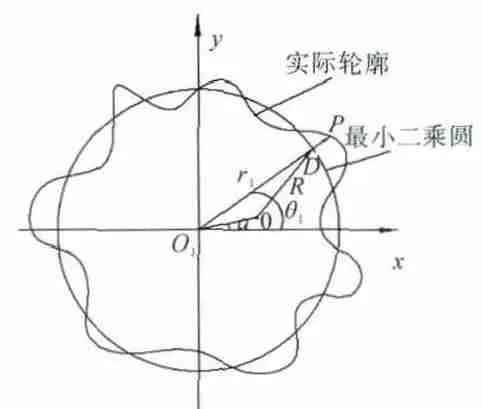
图1 最小二乘中心法原理

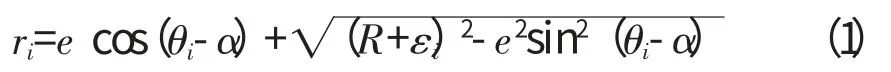
因为

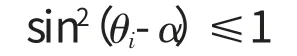
所以

已知

故而

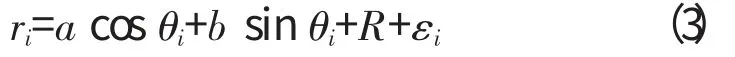
由此可得

根据最小二乘原理有

分别求Q 对R，a，b 的偏导数并令其等于零，可得

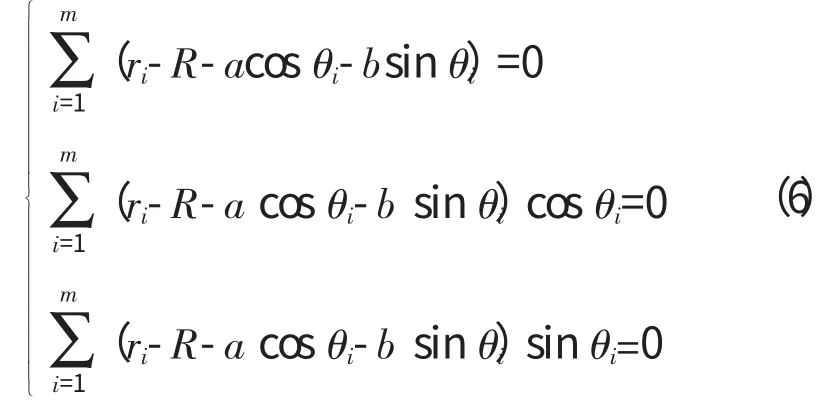
数据的结构矩阵为

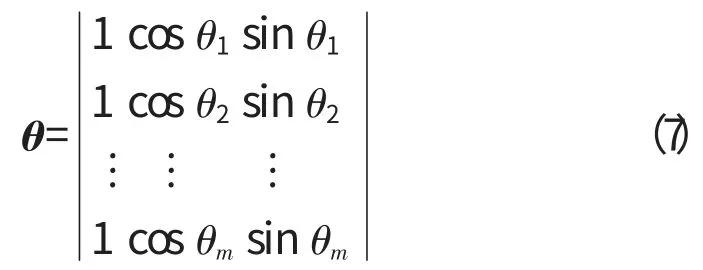
正规方程组的系数矩阵为

又因为A-1A=E

所以

令

则正规方程组的常数项矩阵为

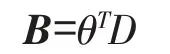
即

设P=|R a b|T则AP=B

所以

即

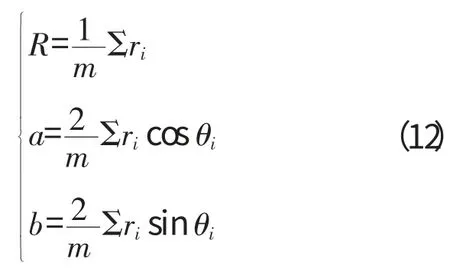
从理论上讲，按上式可求得最小二乘圆的半径R和最小二乘圆圆心坐标分量a、b，令Δri=ri-r0，（i=1，2，…，m），其中r0为任意选定的常量，则有

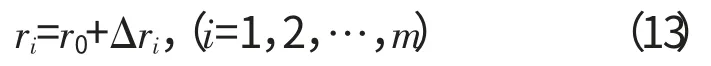
将式（13）代入式（12），即可求出最小二乘圆半径

最小二乘圆圆心的坐标分量为

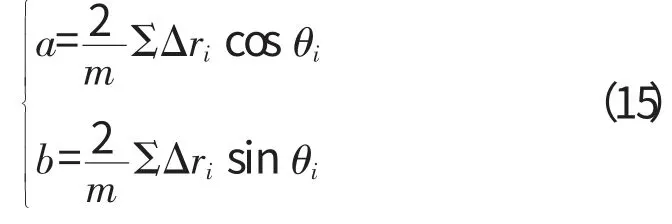
将式（13）和（14）代入式（4），可得

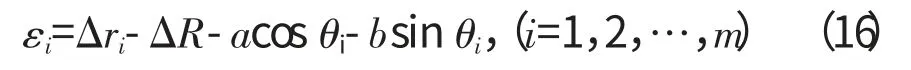
上式表明，若可测得被测圆上各等分离散采样点的半径增量Δri和相应角度θi，便可求得各采样点相对于最小二乘圆的偏差εi。所以最小二乘评定法的圆度误差为

在上面的推导过程中，回转中心与最小二乘中心不重合，所以存在偏心OOl=e，公式εi=ri-R-acos θi-bsinθi是用R+εi代替得到的，下面具体分析由此引起的误差问题。

设误差

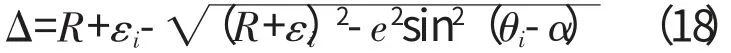
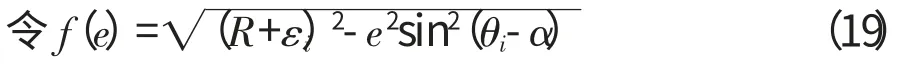
将f（e）展开成泰勒级数

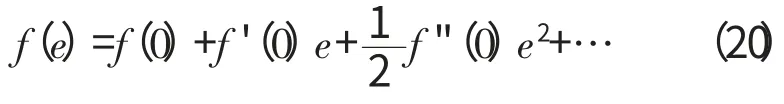
求得

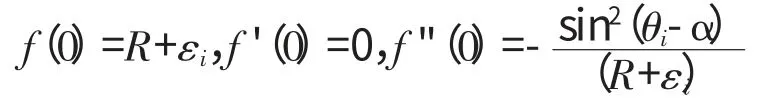
则

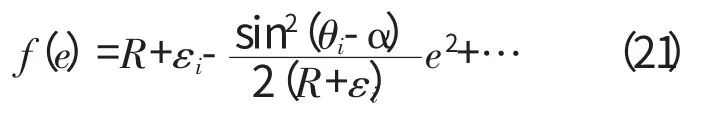
所以

因为sin2（θi-α）≤1，且R+εi=OPi，所以Δmax=即由此引起的误差极小，可以忽略不计，同时证明了求解偏心的数学模型的正确性和可行性。

1.3 叶尖间隙相关特征参数理论模型的建立

如前所述，发动机转、静子叶尖间隙仅由转、静子的中心位置和平均半径差以及转子的回转误差构成。在实际测量中，测得的间隙值是相对回转中心的静子采样点到转子端面的距离，即上述模型中的Δri，相对于回转中心的最大间隙值Δrimax，相对于回转中心的最小间隙值Δrimin。基于1.2节所建立的数学模型建立叶尖间隙数学模型

最大跳动量

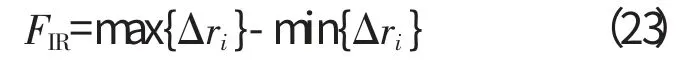
静子内凹点到理想圆的最大值

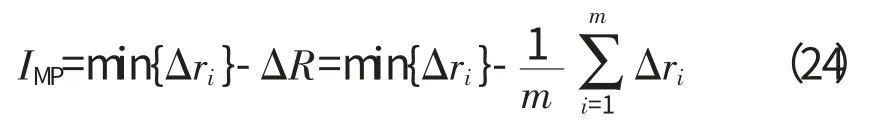
IMP相位即为相对回转中心的最小间隙值即Δrimin的相位。

最小二乘圆心的坐标分量为

通过坐标值即可求得偏心距和偏心角度。

相对于最小二乘圆心的实际间隙值=

相对最小二乘圆心的最大间隙值=

相对最小二乘圆心的最小间隙值=

相对最小二乘圆心的实际间隙变化量=

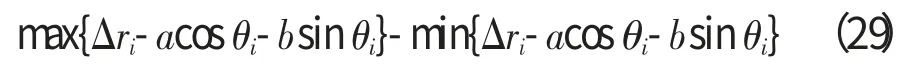
1.4 下沉量修正模型的建立

航空发动机在装配结束后进行间隙测试时分为垂直和水平2种测试状态。在发动机水平放置进行测试时，由于受重力作用整体有1个下沉量，但发动机转子在实际高速旋转时基本与垂直位置比较接近，因此在低速测量数据时，需要排除下沉量对最终数据的影响。

在模型的建立过程中，发动机水平放置时的下沉量为轴承游隙的一半，固其为已知量，根据测得的未修正间隙值和下沉量可计算出修正后即消除下沉量影响的间隙值，数学模型推导过程如下。

修正下沉量原理如图2所示。从图中可见，此时应测量的是转子端面B 点到静子机匣A 点的间隙值Δr'i（O1为下沉前转子回转中心），但由于发动机转子的下沉，测量的实际间隙值为下沉后的转子端面C点到静子机匣A 点的间隙值Δri（O2为下沉后转子回转中心）。下沉量为d，回转中心到转子端面距离为r，即图中的O1B 和O2C 对应A 点的采样角度为α。

在三角形O1O2A 中，由图中几何关系可得

图2 修正下沉量原理

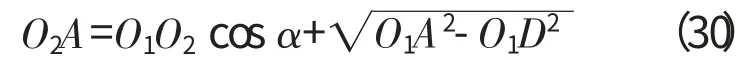
即

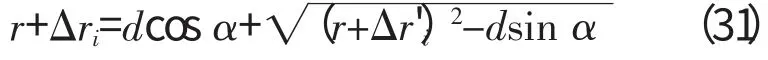
因为

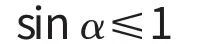
所以

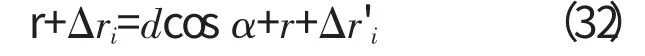
修正后的间隙值为

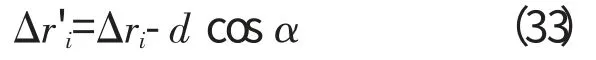
即在发动机水平测试时，需将测得的数据带入上式进行修正后才能带入之前叙述的各模型中来求解其他未知量。

2 航空发动机叶尖间隙数学模型的验证

基于以上数学模型，在LabVIEW平台上开发设计了叶尖间隙数据处理系统软件，具有实时处理数据、自动保存、报表打印、数据查询及间隙放大图等功能（如图3所示）。

将测得的叶尖间隙数据（采样角度－采样间隙值）带入所开发的软件中进行数据处理，可以准确计算出转、静子间的最大和最小间隙值、最大跳动量FIR、采样轮廓内凹点到最小二乘轮廓的最大偏差IMP、最小二乘轮廓中心的坐标分量以及偏心距ECC、相对于最小二乘轮廓中心的实际间隙值以及下沉量修正值等，以及上述各参数的相位角值。将多组数据的计算结果与采用国外成熟软件Linipot的计算结果进行对比分析，绝对误差均小于0.001，相对误差均小于0.005%。其误差的原因均可被认为是计算处理过程中的舍入误差，对最终结果的影响可以忽略。因此，可以断定所进行的理论研究结果正确，所建立的各理论数学模型与国外Linipot软件对应的数学模型一致。

图3 叶尖间隙数据处理主界面

3 结论

叶尖间隙数学模型的建立能够准确计算出最大跳动量FIR、IMP、偏心矩ECC以及下沉量修正值等相关参数，这些参数对于判断发动机转、静子装配是否合格起着关键性作用。通过与国外成熟软件Linipot计算结果进行对比分析，绝对误差均小于0.001，相对误差均小于0.005%。可以断定所进行的理论研究结果正确。

本文方法是国内首次掌握了叶尖间隙数据处理的基本方法，为以后更深入地开展该领域的研究工作奠定了基础。

[1]张娜，黄春峰.航空发动机叶尖间隙测量技术[J].航空制造技术，2010（13）：41-45.ZHANG Na，HUANG Chunfeng.Aircraft engine tip clearance measuring technique[J].Aerospace Manufacturing Technology，2010（13）：41-45.（in Chinese）

[2]陈炳贻.叶尖间隙对航空发动机性能的影响和测量技术[J].燃气涡轮试验与研究，1996（2）：40-44.CHEN Bingyi.Effect of the tip clearance to the aircraft engine performance and measuring technique[J].Gas Turbine Experiment and Research，1996（2）：40-44.（in Chinese）

[3]张玉.圆度误差的最小二乘评定、测量与电算[J].辽宁机械，1985（4）：58-62.ZHANG Yu.The least squares measuring schematics of the roundness[J].Liaoning Machinery，1985（4）：58-62.（in Chinese）

[4]李虹，李伯民.圆度误差测量及误差分析[J].山西机械，2000（1）：44-45.LI Hong，LI Bomin.Roundness error measurement and error analysis[J].Shanxi Machinery，2000（1）：44-45.（in Chinese）

[5]Couey JA，MarshByron E R，Knapp R，et al.Roundness measurement of spherical artifacts at arbitrary latitude[J].Precision Engineering，2006，30：353-356.

[6]商兴国，张帆.圆度误差的快速傅里叶变化分析[J].唐山学院学报，2005，18（3）：88-90.SHANG Xingguo，ZHANG Fan.FFT analysis of the roundness error[J].Journal of College Tangshan，2005，18（3）：88-90.（in Chinese）

[7]Arts T.Turbine blade tip design and tip clearance treatment[R].VKI Lecture Series 2004-2.

[8]Melcher K J.Controls considerations for turbine active clearance control，NASA seals and secondary flow workshop[R].NASA-TM-2003-212533，AIAA-2003-4700.

[9]Gaffin W O.JT9D-70/59 improved high pressure turbine active clearance control system[R].NASA-CR-159661.

[10]Tagashira T.Measurement of blade tip clearance using an ultrasonic sensor[R].AIAA-97-0165.

[11]Wiseman M W，Guo T.An investigation of life extending control techniques for gas turbine engines [C]//American Control Conference，Proceedings of the 2001.New York:IEEE，2001：3706-3707.

[12]Sak V.Advanced thermal HPT clearance control[R].NASA-CP-2004-212963.

[13]郭淑芬，徐波.温度与转速对涡轮叶尖径向间隙的影响[J].推进技术，2000，21（4）：51-53.GUO Shufen，XU Bo.Effect of temperature and rotational speed on radial clearance of turbine blade tip [J].Journal of Proplusion Technology，2000，21（4）：51-53.（in Chinese）

[14]Mayle R E，Metzger D E.Heat transfer at the tip of an unshrouded turbine blade[C]//Proc.Seventh Int.Heat Transfer Conf，Hemisphere Pub：1982：87-92.

[15]Lattime S L，Steinetz B M，Robbie M.Test rig for evaluating active turbine blade tip clearance control concepts[R].NASA-TM-2003-212533，AIAA-2003-4700.