航空发动机整机静子建模与刚度验证

贾瑞琦，曹茂国，梁海涛

（中航工业沈阳发动机设计研究所，沈阳110015）

0 引言

在航空发动机研制、生产和使用过程中，振动问题十分突出[1]。如果要详细地研究发动机整机的振动特性，需将转子、机匣和支架结构等整个系统作为整体进行振动分析。目前国际上的大型航空发动机公司，如GE、PW、RR以及CIAM等均采用专门研发的整机转子动力学计算程序，从理论上指导了新机研制、现有机型的改进和故障分析，缩短了新机型的研发周期，提高了其寿命和可靠性，改善了整机工作性能。

EJ200等先进涡扇发动机建立了用于振动监测和诊断的3维整机有限元模型。对于组成整机模型的各部件，根据其结构特点，采用了不同的分网方法[2]；Armin Schonrock等[3]利用发动机机匣壳体的静刚度测量数据对其有限元模型参数进行了改进；张大义等[4]从计算航空发动机转子系统动力特性的需求方面，讨论了典型支承结构的径向刚度计算中的几个问题；高金海等[5]从计算航空发动机机匣系统动力特性需要以及有限元模型建立的角度，分析了某型涡扇发动机整机动力特性。

在整机有限元模型中，发动机机匣结构因其结构形式复杂，材料多样以及功能差异，建模精度和方式也各有不同。需要采用不同的建模方法针对机匣自身的结构特征以及在整机静子刚度中的贡献程度对机匣部分进行简化[6-10]。

本文以建立整机动力学分析模型为目标，以实际静子结构为研究对象，对比分析了不同简化建模方法对不同结构的影响特征。根据分析结论，建立了发动机整机静子机匣有限元模型，并与试验测量结果进行比较分析和验证，为后续进行整机动力学分析提供静子部分的有限元模型。

1 静子结构

某型航空发动机的主承力构件包括采用整体焊接结构的进气机匣、涡轮后机匣和整体铸造结构的中介机匣，如图1所示。其中主、辅安装节分别置于中介机匣外环水平中心线两侧和加力筒体承力环水平线的一侧。1号轴承座固定于进气机匣内环，承受风扇转子径向和低压转子轴向载荷；2、3号轴承座分别固定于中介机匣内环的前后安装边，分别承受低压径向、高压转子轴向和部分径向的载荷；5号轴承座固定于涡轮后机匣内环[11]。

图1 某型发动机结构

2 结构建模时的简化原则

由于航空技术的发展，转子的转速日益提高，而机匣的壁变薄，且结构大部分为回转壳。转子和机匣之间的联系日趋紧密，二者之间相互耦合及影响日益加强，形成了复杂的动力特性[12]。静子部分作为转子的支承和传力结构，其刚度和质量分布特征对整机转子动力学特性具有显著影响。

无阻尼多自由度系统自由振动的运动方程[13]为

系统频率方程为

由频率方程可知，无阻尼系统的固有频率主要取决于其刚度和质量，所以在简化结构时，只要能保证前后的结构刚度和质量比值不变，且分布相似，便可以保证结构的动力特性不变。因此基本原则为（1）保证部件内部的结构力学关系不变；（2）将部件装配成整机模型时，保证部件之间的传力关系不变；（3）发动机整机模型状态下的质量分布特征不变；（4）最终建立的整机模型应当保证整机的刚度和质量具有一致性。

根据航空发动机在整机状态下的承力和传力特点，静子部件分为主承力机匣和其它机匣。前者是指在机匣部件中装有轴承，直接参与向外传递转子力的部件；后者是指在机匣部件中，不直接参与向外传递转子力的部件。

针对主承力部件结构和受力的复杂情况，建立有限元模型时，需要保留其参与承力的所有主要结构元素，而仅对较小的倒角等结构细节进行简化处理。整机机匣部件建模的难点在于对非承力、局部承力结构以及孔类零部件的建模处理。在对零部件进行建模分析时，在保证结构力学关系不变的前提下有必要对所分析的零部件模型进行局部简化，减少整机系统的单元数，完成对整机模型的计算。

3 静子部件有限元建模方法对比

静子机匣主要为薄壁结构件，有限元建模单元主要包括壳单元和实体单元，对拉杆等杆状部件也可以采用梁单元进行建模。不同部件的建模单元形式和简化方法不同，需要对主承力和其它机匣部件在不同单元类型下的模型有效性和计算规模进行分析。本文以第1级风扇机匣和中介机匣模型为例，分别采用壳单元和实体单元对其建立计算模型，对比2种建模方式在不同承力或传力功能机匣上的有限元计算特点。

3.1 风扇机匣

3.1.1 壳单元几何模型

在壳单元建模过程中，要提取部件模型的中性面作为有限元模型网格划分、材料选取、厚度属性确定的几何壳体。静子叶片形状十分复杂，将叶片沿径向分成若干段，在每段的截面中提取截面的弦线，然后使用UG软件中“通过线生成面（surface—throughcurves）”命令，将弦线和叶片的叶根和叶尖围成的区域生成叶片曲面。对于轴向旋转对称件的机匣壳体，在提取中性面时，可以利用UG软件中的“中性面（midsurface）”命令直接生成。第1级风扇静子机匣的几何壳体模型如图2所示。

图2 第1级风扇机匣壳单元几何模型

3.1.2 实体单元几何模型

在实体单元建模时，可直接利用已经生成的机匣实体几何模型进行网格划分和计算。由于工程需要，在机匣的实际几何模型中存在各种孔洞、倒角、凸台等，在进行实体网格划分时需要在上述部分增加网格密度，极大地增加了划分难度和网格数量。但是根据圣维南原理，对整个模型或整机进行动力学分析可知，上述情况对整体计算结果的影响较小。因此对计算所用的几何实体模型进行简化处理[14]。第1级风扇机匣3维实体几何模型如图3所示。

3.1.3 模型网格划分和属性定义

建立上述2个几何模型后，导入计算软件。根据计算需要定义壳体厚度、材料属性以及部件之间的装配联接关系和边界条件等物理属性。在定义壳体模型机匣壳体厚度时，直接利用壳体对应的实体模型厚度数据。由于风扇静子叶片形状复杂，其厚度沿径向不断变化，并且叶片本身不在整机机匣传力路线上，其主要影响机匣的质量分布状态，定义叶片厚度时，需保证叶片质量和质心分布不发生变化，根据质量等效原则确定叶片自身的厚度。然后采用四边形和三角形网格结合划分。第1级风扇机匣的壳单元网格节点数、单元数和自由度分别为2438、2300、14628。采用六面体网格对实体模型进行网格划分，第1级风扇机匣的3维实体网格节点数、单元数和自由度分别为34040、16606、251574.第1级风扇机匣2种单元网格模型如图4所示。

图3 第1级风扇机匣3维实体几何模型

图4 第1级风扇机匣网格模型

上述模型均采用钛合金的材料数据定义属性。对比2种机匣模型的自由模态，其位移边界条件均为自由边界条件。

3.1.4 计算结果对比分析

在整机传力路线中，不是主承力部件的风扇机匣主要起传递转子受力的作用，其振动特性是确定传递特性的基础。实体单元和壳单元自由振动频率对比如图5所示。2种模型的自由振动频率结果尤其是低阶结果较为接近。

壳单元网格模型的规模要比六面体单元模型的小1个数量级以上，所占用的计算机资源更少，在多个部件模型组装后进行整机动力学分析。因此，计算结果满足工程精度要求时，采用壳单元可以对风扇机匣类部件进行振动模态等动力学分析。在进行整机规模的动力学计算时，在保证工程应用精度的前提下，对传力机匣类部件采用壳单元进行分析，可以大规模缩减整个模型的数据量，减少对计算机资源的需求[15]。

图5 实体单元与壳单元自由振动频率对比

3.2 中介机匣

3.2.1 建模方法

中介机匣壳单元和六面体单元建模的方法、步骤与第1级风扇机匣的相似。壳模型的片体厚度根据其对应的3维模型厚度给出。对厚度变化较大的安装边、轴承腔等采用等效的方式定义其厚度，即根据体积相同的原则得出。实体单元为8节点六面体网格，模型节点数、单元数和自由度分别为44606、26802和363845；采用壳单元为4节点四边形和3节点三角形网格相结合，模型节点数、单元数和自由度分别为2906、2861和18806。相应的网格模型如图6所示。

图6 中介机匣网格模型

采用相同的位移边界条件对2种机匣进行静力学分析。在对2号轴承座施加载荷时，均采用在轴承座安装面上施加集中力的方式。位移边界和载荷条件如图7所示。

3.2.2 计算结果对比分析在相同条件下，2号支点轴承座内表面平均位移对比如图8所示。在相同受力条件下，壳单元模型计算所得的2号支点位移超出实体单元模型的，表明采用壳单元对中介机匣建模时，很大程度上降低了机匣的整体刚性。壳单元和实体单元的横向受力变形如图9所示。从图中可见，在相同边界条件和载荷下，中介机匣的支板相对其内外环在受到拉伸的同时，均有相对的转动。中介机匣的刚性特性主要受到支板刚性以及支板和机匣壳体之间的刚度传递特性影响。对于中介机匣结构，其支板和机匣壁面厚度较大，尤其是支板和机匣壁面的转接部分，已经不符合采用壳单元的薄板理论中厚度远小于其它2个方向尺寸的基本假设，因此仅采用壳单元对中介机匣类结构建模会导致较大的计算误差[15]。

图7 中介机匣静力位移边界和载荷条件

图8 2号支点位移对比

图9 中介机匣模型横向受力变形

通过静力、模态对比分析得出，由于中介机匣中存在较多的安装边和加强结构，为了保证强度要求，大幅度增加厚度已不能较好地符合板壳理论的基本条件。部分采用壳单元时的计算误差将会很大，甚至出现错误结果。

因此，对于中介机匣等发动机主要承力机匣，并不能简单地采用壳单元建模，应采用实体单元的方式来保证计算精度。

4 静子部件建模

针对主承力机匣结构的复杂性和进行响应分析后的结果要求，采用实体单元进行建模。对于其他机匣，为了在保证计算精度的同时尽量减少计算量，主要采用壳单元建模。各机匣都要经过仔细地几何清理以及模型简化甚至重新建立几何模型后，才能导入到计算软件中进行分网。

图10 进气机匣的有限元网络模型

4.1 主承力机匣部件建模

在进气机匣建模时，对于处在传力路线上的结构采用了实体单元，其余的典型壳体件，且不参与轴承传力部分采用了壳单元。进气机匣的有限元网格模型如图10所示。

涡轮后机匣通过8根斜拉杆与外涵承力环相连接。前者均采用梁单元进行建模。在实际部件中，与后机匣外环和外涵承力环的连接方式为铰链式，各拉杆相互约束，使后机匣和外涵承力环在垂直于发动机轴向的平面内的位移相同，而对其他方向的位移并无约束。简化处理对拉杆与后机匣外环和外涵承力环的连接方式，使拉杆与后机匣及外涵承力环铰链装配处的装配副在沿拉杆方向的位移相等，对其他方向的位移并不添加限制。既可以保证后机匣与承力环之间通过拉杆的位移传递，又可以保证使2个机匣在垂直于发动机轴向的平面以外方向的位移具有独立性。涡轮后机匣的有限元网格模型如图11所示。

图11 涡轮后机匣的有限元网络模型

4.2 其他机匣部件建模

利用机匣壳单元建模方法，对风扇、高压压气机、主燃烧室、高压涡轮、低压涡轮、加力燃烧室、收扩喷口以及复合材料外涵等机匣均建立了以壳单元为主体的有限元模型。

图12 风扇机匣

图13 高压压气机机匣

图14 高压涡轮机匣

图15 低压涡轮机匣

图16 燃烧室

图17 加力燃烧室外壳、加力筒体、合流环及尾锥

图18 尾喷口

图19 外涵机匣

对不参与机匣的传力，同时其叶片长度较小，自振频率较高的静子叶片，整级作为单个质量点处理，提取整级叶片的质量、质心、转动惯量等属性，采用集中质量单元的方式将整级叶片装配到其对应的轴线位置处，集中质量单元采用“mean”单元与机匣周围的对应位置连接，模拟其质量分布特征。相应的机匣模型分别如图12～18所示。

以上网格划分所得到的各机匣网格规模和材料属性见表1。

表1 静子部件网格规模和材料

4.3 部件模型的装配

在实际发动机部件中，各机匣部件上都留有安装边，2个相邻的机匣间采用螺栓连接。由于螺栓连接时，机匣安装边的局部受力情况比较复杂，具有一定的非线性。对于整机规模的模型来说，局部非线性的影响范围较小，因此在计算模型中做了简化处理。机匣部件之间的装配采用“点在面上”方式，即在2个进行装配的安装边中的1个安装边节点“黏接”到另1个安装边的面上，可以保证连接面两侧的机匣安装边对应节点处的位移相同；同时不附加限制同一安装边上节点之间的相对位移。

4.4 整机边界条件设定

坐标系定义为z 轴与发动机旋转中心线重合，方向向后为正；y 轴方向向下为正；x 轴由y 轴到z 轴按右手法则确定。

根据发动机的台架安装方式，计算模型的位移边界条件设置方式为中介机匣顺航向看右侧主安装节处约束其沿x、y、z 方向的平动位移，左侧主安装节约束y、z 方向的平动位移，2个安装节上均不限定其以安装节连线方向为轴的转动。加力筒体吊耳处约束y方向平动位移，不限定吊耳处的转动自由度。

按照整机机匣静柔度试验时的加载方式，分别沿x、y 方向，在1～3、5号支点的轴承座中心面上施加10 kN的作用力，计算发动机机匣整体状态下的变形。

机匣承力系统的有限元模型如图20所示。

图20 机匣承力系统有限元模型

5 计算结果

利用已建立的整机机匣有限元模型，计算了发动机整机状态下的各支点的静柔度，并将计算结果与试验结果进行了对比分析。

最终计算所得的各支点相对于发动机主安装节的静柔度相对值见表2。

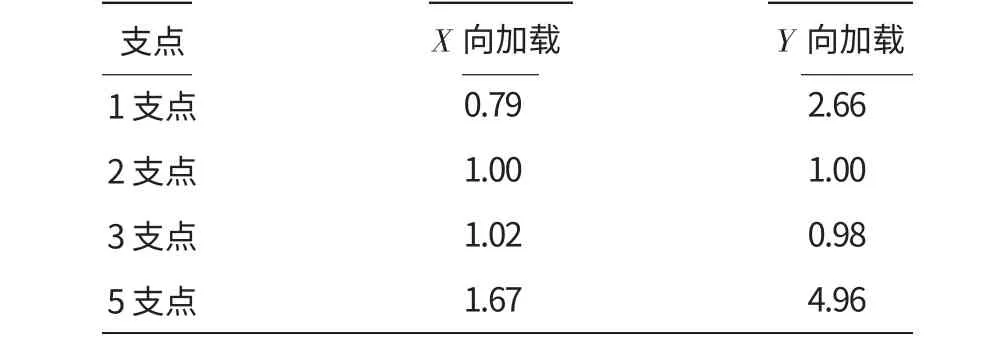
表2 各支点相对于发动机主安装节静柔度值

6 静柔度试验及结果对比

对承力系统静柔度进行试验，测量了承力系统1～3、5支点的静柔度。

6.1 试验项目及载荷

分别在某型发动机的1～3、5的轴承中截面处施加横向力，测量轴承中截面的横向位移，计算轴承相对于主安装节的静柔度。在室温条件下，按照台架试车要求安装在发动机专用静力试验台上进行试验。

6.2 试验加载方式和测量方案

1支点静柔度试验加载装置（局部）如图21所示。从图中可见，横向力加载螺杆1和3通过杠杆5、关节轴承和模拟轴承7对1号轴承座施加横向载荷，测力计2、4的差值为横向载荷。其他支点位置的加载方式与1号轴承座类似。

图21 1支点静柔度试验加载装置（局部）

6.3 计算结果与试验结果

整机支点柔度计算与试验结果见表3。

表3 整机支点柔度计算与试验对比

从表中可见，1～3支点的柔度计算值与试验值相对于主支点的相差较小。5支点的柔度计算值与试验值相对于主支点的相差较大，相对误差分别为17%（X 向）和19%（Y 向）。

5支点位于涡轮后机匣，通过在同一平面内（垂直于轴向的平面）的8根斜杆与外涵承力机匣连接。该装配方式使5支点的径向静柔度特性具有较强的非线性，在试验加载过程中也发现了该现象。在整机机匣的静刚度计算中，模拟拉杆与机匣的装配关系时进行了线性简化，仅限定参与拉杆与机匣装配处的节点位移沿拉杆方向相同，不限定装配处节点其他方向的位移。与实际装配关系相比，降低了机匣产生相对位移时涡轮后机匣与外涵承力机匣之间的刚性，使得5支点的柔度计算值大于试验测量值。

7 结论

通过对比不同功能机匣建模方式，将各主要静子部件的有限元模型组装成整机模型，并进行了整机状态下各支点的静柔度计算，得到如下结论。

（1）对静子建模可以分为主承力机匣部件和其他机匣部件分别进行。对机匣建模时，可以采用壳单元或实体单元。相同结构壳单元的网格数目比3维单元的有较大幅度地减少；

（2）主承力机匣结构比较复杂，并且直接传递转子作用力。因此需要采用实体单元进行建模，保证模型的有效性。其他机匣基本为壳体类部件，受力情况也比主承力机匣的简单，可以采用壳单元建模；

（3）发动机整机有限元模型计算与试验得出各支点在横、纵向的柔度值差值在工程精度范围内。有限元模型与实际发动机的刚度分布符合较好，经过质量修正后，可以作为发动机整机振动计算中的静子模型参与计算。

[1]李文明.新机研制中整机振动及其限制值实践与思考[J].航空发动机，2002，（2）:22-26.LI Wenming.Engine vibration and its limit in development of new engine practice and consideration[J].Aeroengine，2002，（2）:22-26.(in Chinese)

[2]Moreno Barragan J A.Investigations into engine transient response due to internal and external dynamic excitations[R/OL].MTU Aero Engines GmbH，Engine Dynamics.[2014-05-25].http：//www.mtu.de/company/mtu-worldwide/mtu-aero-engines-polska/.

[3]Schonrock A，Dascotte E，Dufour K H.Validation of an aeroengine carcass finiteelementmodel bymeansof computational model updatingbased on static stiffness testing [R/OL].BMW Rools-Royce AeroEngines，[2014-05-25].http：//www.femtools.com/download.php?id=epf99/.

[4]张大义，母国新，洪杰.航空发动机转子支承系统刚度计算中的几个问题[J].战术导弹技术，2005（2）：20-23.ZHANG Dayi，MU Guoxin，HONG Jie.Rigidity calculation methods for rotor supporting system in aeroengine[J].Tactical Missile Technology，2005（2）：20-23.(in Chinese)

[5]高金海，洪杰.航空发动机整机动力特性建模技术研究[J].战术导弹技术，2006（2）：29-35.GAO Jinhai，HONG Jie.Study of modeling technique for dynamic characteristics of engine casing[J].Tactical Missile Technology，2006（2）：29-35.(in Chinese)

[6]陈萌，马燕红，刘书国，等.航空发动机整机有限元模型转子动力学分析[J].北京航空航天大学报，2007，33（9）：1013-1016.CHEN Meng，MA Yanhong，LIU Shuguo，et al.Rotordynamic analysis of whole aero-engine models based on finite element method[J].Journal of Beijing University of Aeronautics and Astronautics，2007，33（9）：1013-1016.(in Chinese)

[7]Zang C，Schwingshackl CW，Ewins D J.Model validation for structural dynamic analysis：an approach to the sandia structural synamics challenge[J].Computer Methods in Applied Mechanics and Engineering，2008（197）：2645-2659.

[8]晏砺堂，朱梓根.结构系统动力特性分析[M].北京：北京航空航天大学出版社，1987：25-26.YAN Litang，ZHU Zigen.Dynamics analysis of structures[M].Beijing：Beihang University Press，1987：25-26.(in Chinese)

[9]晏砺堂.航空燃气轮机振动和减振[M].北京：国防工业出版社，1991:30-31.YAN Litang.Vibration characteristics and decreasing method of aeroengine[M].Beijing：National Defense Industry Press，1991:30-31.(in Chinese)

[10]付才高.转子动力学及整机振动[M].北京：航空工业出版社，2000：34.FU Caigao.Rotor dynamics and whole engine vibration[M].Beijing：Aviation Industry Press，2000：34.(in Chinese)

[11]刘长富，邓明.航空发动机结构分析[M].西安：西北工业大学出版社，2006:21.LIU Changfu，DENG Ming.Structural analysis of aeroengine[M].Xi’an：Northwestern Polytechnical University Press，2006:21.(in Chinese)

[12]陈果.航空发动机整机振动耦合动力学模型及其验证[J].航空动力学报，2012，27（2）:241-254 CHEN Guo.A coupling dynamic model for whole aeroengine vibration and its verification[J].Journal of Aerospace Power，2012，27（2）：241-254(in Chinese)

[13]郑旭东，张连祥，刘廷毅.航空发动机整机振动特性及应变能计算与分析[J].航空发动机，2000，26（2）：42-46.ZHENG Xudong，ZHANG Lianxiang，LIU Tingyi.Whole engine vibration characteristics and strain energy analysis of aeroengine[J].Aeroengine，2000，26（2）：42-46.(in Chinese)

[14]周传月.SAMCEF有限元分析及应用实例[M].北京：机械工业出版社，2009:35.ZHOU Chuanyue.Finite element analysis and application example of SAMCEF[M].Beijing：China Machine Press，2009:35.(in Chinese)

[15]曾攀.有限元分析及应用[M].北京：清华大学出版社，2004：76.ZENG Pan.Finite element analysis and applications[M].Beijing：Tsinghua University Press，2004：76.(in Chinese)