齿轮驱动涡扇发动机星型齿轮减速器安装角度计算与分析

冯 金，章焕章，娄 鹏，罗 健

（中航商用航空发动机有限责任公司，上海201108）

0 引言

高涵道比双转子涡扇发动机自20世纪70年代初投入使用以来，与风扇相连的低压压气机和低压涡轮受风扇叶尖切线速度限制，只能在较低转速下运行，导致压气机级数增加、质量大且效率低。为此，可在由低压压气机和低压涡轮组成的低压转子与风扇转子间安装1套齿轮减速器，使风扇转子在低转速下工作，而低压转子在高转速下工作，构成齿轮驱动涡扇发动机（GearedTurbofan）[1-2]。目前采用此构型的涡扇发动机主要为美国PW 公司的清洁动力（PurePowerTM）PW1000G系列发动机[3-5]。中国对上述发动机的研究尚处于预研阶段[6-8]，只进行了相关理论研究，如沈阳发动机设计研究所对齿轮驱动涡扇发动机的设计特点进行了分析[9]，中国燃气涡轮研究院对基于流量法的齿轮传动涡扇发动机动态性能建模技术展开了研究[10]。

齿轮传动涡扇发动机与传统2轴涡扇发动机最主要区别在于风扇和低压转子之间的齿轮减速器，相比船舶[11-12]及风电等其它领域，在航空领域[13-14]中，特别是在涡扇发动机中使用的齿轮减速器载荷大、转速高、寿命长，设计难度较大，在国内处于理论研究阶段[15-16]。

本文以齿轮驱动涡扇发动机5路分流星型齿轮减速器为研究对象，对在齿轮减速器重力载荷及人字齿轮啮合扭矩作用下传扭支架的受力情况进行分析，通过理论计算确定了星型齿轮减速器的安装角度并使用有限元方法对计算结果进行验证。

1 星型齿轮减速器结构

星型齿轮减速器主要由太阳轮、行星轮、外齿圈、轴承、行星架及传扭支架等零组件构成，如图1所示。减速器外廓尺寸约为Φ880mm×680mm，传动比约为3∶1，传递功率大于40000kW。外齿圈作为输出端，通过螺栓与风扇轴连接；太阳轮作为输入端，与输入轴通过花键连接；整个齿轮箱的重力及齿轮啮合时产生的扭矩通过行星架由支架连杆传递给传扭支架。

图1 星型齿轮减速器结构

2 重力载荷对安装角度的影响

5个支架连杆均匀分布，传扭支架的受力受减速器安装角度影响。根据前期计算可知，由齿轮啮合力传导到支架连杆根部的应力远大于齿轮箱重力作用在支架连杆根部的应力，且减速器的姿态只有在飞行过程中才会发生变化，因此仅考虑减速器在水平放置时其重力对传扭支架受力的影响。

设支架连杆i 与圆心连线，方向指向圆心，重力方向竖直向下，支架连杆i与圆心连线逆时针旋转至重力方向的转角为αi。当齿轮箱安装角度固定时，传扭支架也同时固定。设任意支架连杆位于顺航向9点钟位置时为齿轮箱初始安装位置，如图2所示。

根据图中几何关系可知

图2 支架连杆周向角度

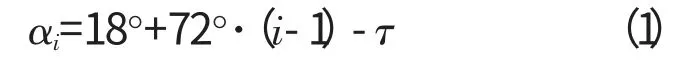
式中：τ 为传扭支架在任意安装角度时其相对初始位置逆时针旋转的角度，0°≤τ<72°。

为便于计算，假设图2中支架连杆截面为长方形，长度为H，宽度为B，x'轴穿过其形心且平行于x轴，y'轴穿过其形心且平行于y 轴，截面内任意点相对x'轴的距离为y，连杆截面相对x'轴的惯性矩为Ix'，抗弯截面系数为Wx'。

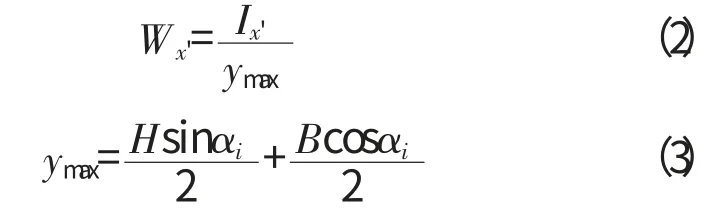
设αi=0时，连杆截面相对x'轴的惯性矩为Ix，相对y'轴的惯性矩为Iy，则Ix'为

其中

令H=10cm，B=2cm，则抗弯截面系数Wx'随αi的变化如图3所示。

由从图3中可见，当αi≈5°时，支架连杆的抗弯截面系数最小；当αi=90°时，支架连杆的抗弯截面系数最大。由于抗弯强度随抗弯截面系数增大而提高，为使支架连杆均匀承受行星架的重力，要求αi尽量接近90°。为方便计算，将αi锐角化为α'i。

当-90°≤αi<90°时

图3 抗弯截面系数Wx'随αi变化

当90°≤αi<180°时

当180°≤αi<270°时

当270°≤αi<360°时

此时，对αi的要求转变为对α'i的要求，即要求α'i尽量接近90°，当τ 逐渐增大时，α'i的变化如图4所示。

为方便显示，令β=min（α'i），则当β 逐渐增大时，的变化如图5所示。

图4 支架连杆夹角α'i随τ 的变化

图5 支架连杆最小夹角β随τ 的变化

从图5中可见，当τ=0°、36°时，即当任意1个支架连杆位于3点钟或9点钟方向时，β 取值最大；当τ=18°、54°时，即当任意1个支架连杆位于6点钟或12点钟方向时， 取值最小。使用有限元软件对上述结论进行分析，对行星架施加不同方向重力并将行星齿轮以质量点的形式平均施加于轴承座上，模拟不同安装角度下传扭支架的受力状况，如图6所示：支架连杆I位于6点钟方向，依次加载不同方向的重力载荷1至重力载荷6。

设重力载荷方向与垂直方向的夹角为θ，取值分别为0°、18°、24°、36°、48°、60°。不同重力载荷下支架连杆根部的应力分布如图7所示。

图6 传扭支架所受重力方向

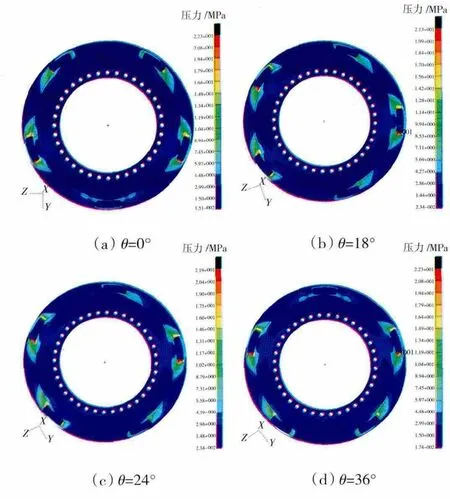
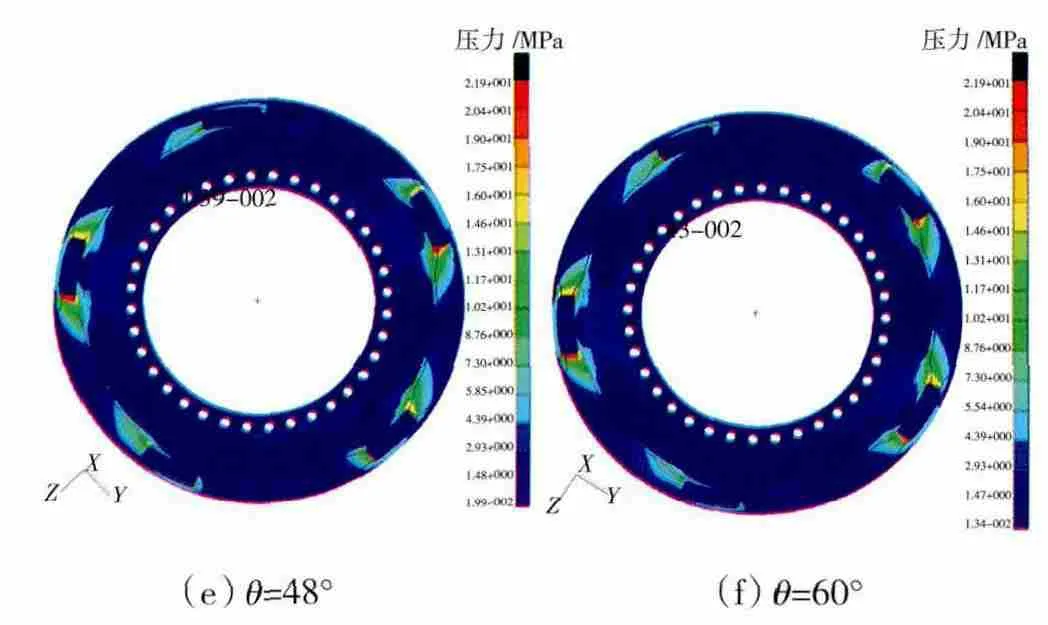
图7 不同重力载荷下支架连杆根部应力分布

为便于计算，统计不同重力载荷下支架连杆根部所受最大应力，连杆根部应力变化如图8所示。

由上述计算结果可知，仅考虑重力载荷，齿轮箱的安装角度对传扭支架所受最大应力的影响较小。此外，在θ=0°、36°时，支架连杆根部出现最大应力，即当任意1个支架连杆位于6点钟或12点钟方向时，支架连杆根部出现最大应力；在θ=18°、54°时，支架连杆根部出现最小应力，即当任意1个支架连杆位于3点钟或9点钟方向时，支架连杆根部出现最小应力。上述结论与之前的计算结果一致，即在仅考虑重力载荷的作用下，为减小传扭支架所受最大应力，需避免使重力载荷垂直通过任一支架连杆。此外，当重力通过2个相邻支架连杆夹角的1/4处时，支架连杆根部所受最大应力最小。因此，安装星型齿轮箱时，将任意支架连杆置于3点钟或9点钟方向，可使传扭支架受重力载荷影响最小。

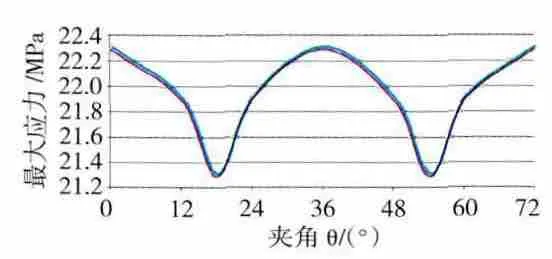
图8 连杆根部应力变化

3 啮合扭矩对安装角度的影响

行星轮齿轮轴轴承受到的齿轮啮合力会对行星架产生与太阳轮转动方向相同的啮合扭矩并传递至传扭支架。设齿轮啮合力由行星架传递给传扭支架的啮合扭矩为T；支架连杆到太阳轮轴心的距离为D，长度为L，宽度为H，厚度为B，如图9所示。

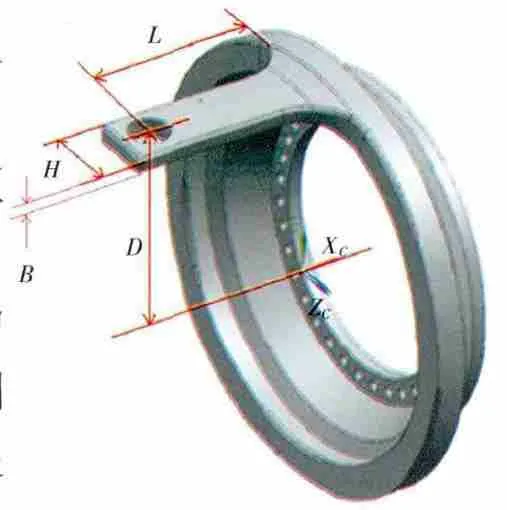
图9 支架连杆尺寸

在不考虑结构误差的情况下，啮合扭矩在支架连杆根部产生的等效拉应力为Fl，等效压应力为Fy。

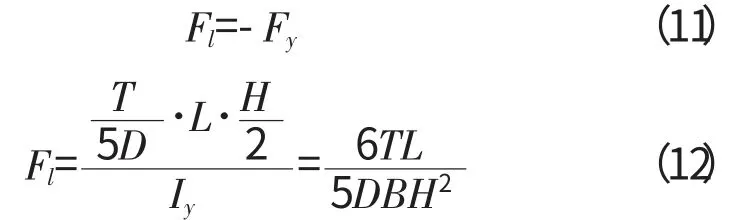
由式（11）、（12）可知，啮合扭矩在支架连杆根部产生的等效拉应力和压应力大小相等、方向相反，故在理想状态下啮合扭矩本身对安装角度无影响。

4 综合影响分析

综合考虑重力载荷和啮合扭矩对安装角度的影响，可将由重力载荷作用在支架连杆根部的应力与由啮合扭矩作用在支架连杆根部的应力进行叠加。啮合扭矩本身对安装角度无影响，可从2种应力方向的异同判断安装角度。

支架连杆处于3点钟位置且啮合扭矩为顺时针的情况与支架连杆处于9点钟位置且啮合扭矩为逆时针的情况相近，支架连杆处于3点钟位置且啮合扭矩为逆时针的情况与支架连杆处于9点钟位置且啮合扭矩为顺时针的情况相近，故仅针对支架连杆处于3点钟位置时所受啮合扭矩的情况进行分析。

扭矩及重力对支架连杆根部作用力的方向如图10所示。蓝色箭头朝上表示重力载荷在支架连杆根部产生的拉应力，蓝色箭头朝下表示重力载荷在支架连杆根部产生的压应力，红色箭头朝上表示啮合扭矩在支架连杆根部产生的拉应力，红色箭头朝下表示重力载荷在支架连杆根部产生的压应力，啮合扭矩方向基于发动机顺航向定义。支架连杆在3点钟位置受到逆时针啮合扭矩作用时，行星架重力载荷及啮合扭矩作用在支架连杆根部的作用力方向有3处相同，2处相反；支架连杆在3点钟位置受到顺时针啮合扭矩作用时，行星架重力载荷及啮合扭矩作用在支架连杆根部的作用力方向有2处相同，3处相反。为使支架连杆根部受力均匀，应选择受力方向为3处相反的，即当啮合扭矩为顺时针时，支架连杆处于3点钟位置，当啮合扭矩为逆时针时，支架连杆处于9点钟位置。

图10 扭矩及重力对支架连杆根部作用力的方向

对支架连杆处于3点钟位置时所受啮合扭矩的情况进行有限元分析，设齿轮啮合时单个行星轮所受到的径向力为290kN，其产生的扭矩连同整个齿轮箱的重力作用在支架连杆根部时的受力情况如图11所示。

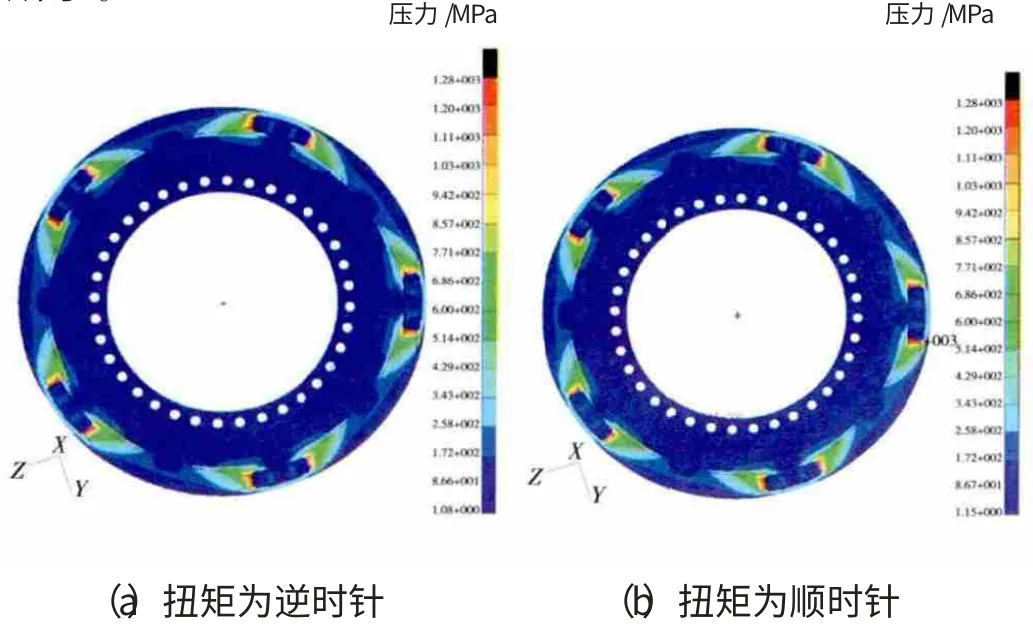
图11 扭矩及重力对支架连杆根部作用力

将3点钟位置支架连杆上端根部最大应力编号为1，其余根部最大应力按逆时针依次编号，则图11中各连杆根部最大应力见表1。

表1 连杆根部最大应力 MPa

从表1中可见，当任意支架连杆位于3点钟位置且扭矩为逆时针时，在连杆根部产生最大应力。因此当啮合扭矩为顺时针时，应使支架连杆处于3点钟位置；当啮合扭矩为逆时针时，应使支架连杆处于9点钟位置。该有限元分析结果与角度分析结果结论相同。

4 结论

根据理论计算及仿真结果得到以下结论：

（1）仅考虑齿轮减速器重力载荷的情况下，齿轮减速器安装角度对传扭支架根部所受最大应力的影响较小。当任意支架连杆处于12点钟或6点钟位置时，支架连杆根部出现最大应力；当任意支架连杆处于3点钟或9点钟位置时，支架连杆根部出现最小应力。

（2）为使支架连杆根部应力最小，当齿轮啮合扭矩为顺航向顺时针时，应使任意支架连杆处于3点钟位置；当齿轮啮合扭矩为顺航向逆时针时，应使支架连杆处于9点钟位置。

[1]Kurzke J，Kurzke J.Fundamental differences between conventional and geared turbofans[C]//ASME Turbo Expo 2009：Power for Land，Sea，and Air，Florida，USA：American Society of Mechanical Engineers，2009：145-153.

[2]Riegler C，Bichlmaier C.The geared turbofan technology-opportunities，challenges and readiness status[C]//Proceedings of the 1st CEAS European Air and Space Conference，Berlin，Germany：The Council of the European Aerospace Societies，2007：156.

[3]陈光.齿轮传动风扇PW 8000高涵道比涡轮风扇发动机[J].民航经济与技术，1998（5）：37-39.CHEN Guang.An introduction of PW8000[J].Civil Aviation，1998（5）：37-39.(in Chinese)

[4]李杰.清洁动力PW1000G发动机发展历程与技术特点分析[J].航空科学技术，2009（5）：3-6.LI Jie.Development history and technical analysis on PW 1000G engine[J].Aeronautical Science and Technology，2009（5）：3-6.(in Chinese)

[5]陈光.PW1000G齿轮传动风扇发动机设计特点[J].国际航空，2009（12）：71-74.CHEN Guang.Design features of PW1000G GTF engine[J].International Aviation，2009（12）：71-74.(in Chinese)

[6]李杰.齿轮传动涡轮风扇(GTF)发动机先进技术综述[J].航空发动机，2009，35（4）：55-58.LI Jie.Overview of advanced technology for geared turbofan engine[J].Aeroengine，2009，35（4）：55-58.(in Chinese)

[7]聂晶，杨瑾，童悦.大型民机发动机关键技术现状与发展趋势[J].航空制造技术，2012（21）：34-37.NIE Jing，YANG Jin，TONG Yue.Key technology and development of large civil aircraft engine[J].Aeronautical Manufacturing Technology，2012（21）：34-37.(in Chinese)

[8]黄春峰，姚艳玲，蒋明夫.GTF发动机技术性能和应用前景分析[J].航空制造技术，2012（13）：44-48.HUANG Chunfeng，TAO Yanling，JIANGMingfu.Analysis on technical performance and application prospect of GTF engine[J].Aeronautical Manufacturing Technology，2012（13）：44-48(in Chinese)

[9]张德志，张锦绣，王凤.齿轮驱动涡扇发动机结构设计特点分析[J].航空发动机，2011，37（4）：1-4.ZHANG Dezhi，ZHANG Jinxiu，WANG Feng.Analysis of structural design characteristics for geared turbofan engine[J].Aeroengine，2011，37（4）：1-4(in Chinese)

[10]童万军，唐世建.基于流量法的齿轮传动涡扇发动机动态建模[J].航空动力学报，2011，26（6）：1377-1383.TONG Wanjun，TANG Shijian.Geared turbofan engine transient modeling research based on CMF method[J].Journal of Aerospace Power，2011，26（6）：1377-1383.(in Chinese)

[11]尹素格.船用星型齿轮减速器的均载与动态特性研究[D].哈尔滨：哈尔滨工程大学，2011.YIN Suge.Research on load sharing and dynamic characteristics of marine star gear reducer[D].Harbin：Harbin Engineering University，2011.(in Chinese)

[12]蒋立冬，岳彦炯，尹素格.星型齿轮箱动响应的分析与计算[J].机械传动，2012，36（8）：51-53.JIANG Lidong，YUE Yanjiong，YIN Suge.The analysis and calculation of dynamic response of star gearbox[J].Journal of Mechanical Transmission，2012，36（8）：51-53.(in Chi-nese)

[13]孟祥战.航空发动机星型齿轮传动系统优化设计[D].南京：南京航空航天大学，2004.MENG Xiangzhan.Optimization of two-stage star-type gear transmission system[D].Nanjing：Nanjing University of Aeronautics and Astronautics，2004.(in Chinese)

[14]方宗德，沈允文，黄镇东.三路功率分流恒星式减速器的动态特性[J].航空学报，1990，11（7）：341-350.FANG Zongde，SHEN Yunwen，HUANG Zhendong.The dynamic behavior of star gearing with three branches[J].Acta Aeronautica et Astronautica Sinica，1990，11（7）：341-350.(in Chinese)

[15]陈聪慧，信琦.风扇齿轮驱动系统的概念设计[J].航空科学技术，2011（4）：8-11.CHEN Conghui，XIN Qi.Conceptual design of fan gear drive system[J].Aeronautical Science and Technology，2011（4）：8-11.(in Chinese)

[16]孙智民，沈允文.星型齿轮传动非线性动力学建模与动载荷研究[J].航空动力学报，2001，16（4）：402-408.SUN Zhimin，SHEN Yunwen.Research on the nonlinear dynamic modeling and dynamic load of star gear transmission[J].Journal of Aerospace Power，2001，16（4）：402-408(in Chinese)